吉林省重点中学2011届高三第一次模拟考试数学(理)试题
文档属性
| 名称 | 吉林省重点中学2011届高三第一次模拟考试数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 286.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-06 15:26:47 | ||
图片预览




文档简介
A 卷
一、选择题(本大题共12小题,每小题5分,共计60分)
1.已知集合,,则集合 ( )
A. B.
C. D.
2.复数 (i是虚数单位的实部是 ( )
A. B. C. D.
3.命题“若”的逆否命题是 ( )
A.若 B.若
C.若则 D.若
4.函数的定义域为 ( )
A. B. C. D.
5.下列命题中,真命题的是 ( )
A. B.
C. D.
6.命题甲:p是q的充分条件;命题乙:p是q的充分必要条件,则命题甲是命题乙的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.从总数为N的一群学生中抽取一个容量为100的样本,若每个学生被抽取的概率为,则N的值 ( )
A.25 B.75 C.400 D.500
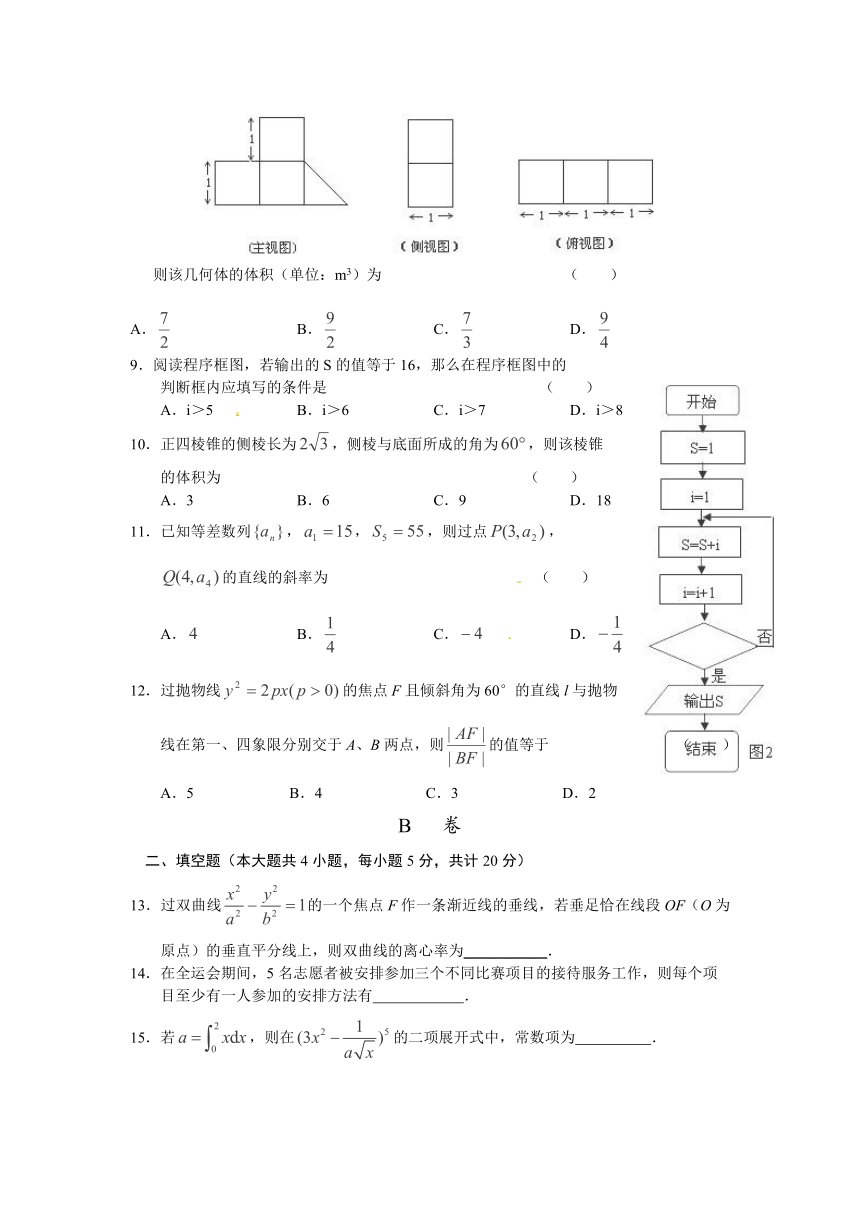
8.一空间几何体按比例绘制的三视图如图所示(单位:m)
则该几何体的体积(单位:m3)为 ( )
A. B. C. D.
9.阅读程序框图,若输出的S的值等于16,那么在程序框图中的
判断框内应填写的条件是 ( )
A.i>5 B.i>6 C.i>7 D.i>8
10.正四棱锥的侧棱长为,侧棱与底面所成的角为,则该棱锥
的体积为 ( )
A.3 B.6 C.9 D.18
11.已知等差数列,,,则过点,
的直线的斜率为 ( )
A. B. C. D.
12.过抛物线的焦点F且倾斜角为60°的直线l与抛物
线在第一、四象限分别交于A、B两点,则的值等于 ( )
A.5 B.4 C.3 D.2
B 卷
二、填空题(本大题共4小题,每小题5分,共计20分)
13.过双曲线的一个焦点F作一条渐近线的垂线,若垂足恰在线段OF(O为原点)的垂直平分线上,则双曲线的离心率为___________.
14.在全运会期间,5名志愿者被安排参加三个不同比赛项目的接待服务工作,则每个项
目至少有一人参加的安排方法有 .
15.若,则在的二项展开式中,常数项为 .
16.设是一个公差为(>0)的等差数列.若,且其前6项的和,则= .
三、解答题(本大题共6小题,共计70分)
17.(本小题满分12分)
已知函数的最小正周期为.
(Ⅰ)求;
(Ⅱ)当时,求函数的值域.
18.(本小题满分12分)
某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示.
(Ⅰ)求甲、乙两名运动员得分的中位数;
(Ⅱ)你认为哪位运动员的成绩更稳定?
(Ⅲ)如果从甲、乙两位运动员的7场得分中各随机抽取一场的得分,求甲的得分大于乙的得分的概率.
19.(本小题满分12分)
已知等腰直角三角形,其中∠=90 ,.点、分别是、的中点,现将△沿着边折起到△位置,使⊥,连结、.
(Ⅰ)求证:⊥;
(Ⅱ)求二面角的余弦值.
20.(本小题满分12分)
设椭圆的离心率,右焦点到直线的距离为坐标原点.
(Ⅰ)求椭圆的方程;
(II)过点作两条互相垂直的射线,与椭圆分别交于两点,证明:点到直线的距离为定值,并求弦长度的最小值.
21.(本小题满分12分)
已知函数(为常数),直线l与函数的图象都相切,且l与函数的图象的切点的横坐标为l.
(Ⅰ)求直线l的方程及a的值;
(Ⅱ)当k>0时,试讨论方程的解的个数.
请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.
22.(本小题满分10分)
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.
(Ⅰ)求证:△ABE≌△ACD;
(Ⅱ)若AB=6,BC=4,求AE.
23.(本小题满分10分)
已知函数.
(Ⅰ)解不等式≤4;
(Ⅱ)若存在x使得≤0成立,求实数a的取值范围.
24.(本小题满分10分)
已知直线l经过点P(1,1),倾斜角.
(Ⅰ)写出直线l的参数方程
(Ⅱ)设l与圆x2+y2=4相交与两点A、B,求点P到A、B两点的距离之积.
参考答案
18.解:(Ⅰ)运动员甲得分的中位数是22,运动员乙得分的中位数是23………2分
(Ⅱ)…………………3分
…………………4分
…………………………………………………………………………………5分 ……………………………………………………………………………………………6分
,从而甲运动员的成绩更稳定………………………………7分
(Ⅲ)从甲、乙两位运动员的7场得分中各随机抽取一场的得分的基本事件总数为49
……8分
∵ ,
∴ ⊥平面. …… 4分
∵ 平面,
∴ . …… 6分
(Ⅱ)建立如图所示的空间直角坐标系.
则(-1,0,0),(-2,1,0),
(0,0,1).∴=(-1,1,0),
=(1,0,1), ……8分
设平面的法向量为,则
∴ 二面角的余弦值是. ………………12分
20.解:(I)由
由右焦点到直线的距离为
即
即弦AB的长度的最小值是 …………13分
21.解:(1)
比较①和②的系数得。
(2)
-1 (-1,0) 0 (0,1) 1
+ 0 - 0 + 0 -
↗ 极大值ln2 ↘ 极小值 ↗ 极大值ln2 ↘
由函数在R上各区间上的增减及极值情况,可得
(1)当时有两个解;
(2)当时有3个解;
(3)当时有4个解
(4)当k=ln2时有2个解;
(5)当时无解。
22.(本小题满分10分)选修4-1:几何证明选讲
解:(Ⅰ)在ΔABE和ΔACD中,
∵ ∠ABE=∠ACD………………2分
又,∠BAE=∠EDC
∵BD//MN
∴∠EDC=∠DCN
∵直线是圆的切线,
∴∠DCN=∠CAD
∴∠BAE=∠CAD
(2)把直线代入
得
2,4,6
1
2
3
2
3
3
7
1
0
1
4
7
5
4
2
3
2
甲
乙
(第19题图)
②③②
①③②
一、选择题(本大题共12小题,每小题5分,共计60分)
1.已知集合,,则集合 ( )
A. B.
C. D.
2.复数 (i是虚数单位的实部是 ( )
A. B. C. D.
3.命题“若”的逆否命题是 ( )
A.若 B.若
C.若则 D.若
4.函数的定义域为 ( )
A. B. C. D.
5.下列命题中,真命题的是 ( )
A. B.
C. D.
6.命题甲:p是q的充分条件;命题乙:p是q的充分必要条件,则命题甲是命题乙的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.从总数为N的一群学生中抽取一个容量为100的样本,若每个学生被抽取的概率为,则N的值 ( )
A.25 B.75 C.400 D.500
8.一空间几何体按比例绘制的三视图如图所示(单位:m)
则该几何体的体积(单位:m3)为 ( )
A. B. C. D.
9.阅读程序框图,若输出的S的值等于16,那么在程序框图中的
判断框内应填写的条件是 ( )
A.i>5 B.i>6 C.i>7 D.i>8
10.正四棱锥的侧棱长为,侧棱与底面所成的角为,则该棱锥
的体积为 ( )
A.3 B.6 C.9 D.18
11.已知等差数列,,,则过点,
的直线的斜率为 ( )
A. B. C. D.
12.过抛物线的焦点F且倾斜角为60°的直线l与抛物
线在第一、四象限分别交于A、B两点,则的值等于 ( )
A.5 B.4 C.3 D.2
B 卷
二、填空题(本大题共4小题,每小题5分,共计20分)
13.过双曲线的一个焦点F作一条渐近线的垂线,若垂足恰在线段OF(O为原点)的垂直平分线上,则双曲线的离心率为___________.
14.在全运会期间,5名志愿者被安排参加三个不同比赛项目的接待服务工作,则每个项
目至少有一人参加的安排方法有 .
15.若,则在的二项展开式中,常数项为 .
16.设是一个公差为(>0)的等差数列.若,且其前6项的和,则= .
三、解答题(本大题共6小题,共计70分)
17.(本小题满分12分)
已知函数的最小正周期为.
(Ⅰ)求;
(Ⅱ)当时,求函数的值域.
18.(本小题满分12分)
某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示.
(Ⅰ)求甲、乙两名运动员得分的中位数;
(Ⅱ)你认为哪位运动员的成绩更稳定?
(Ⅲ)如果从甲、乙两位运动员的7场得分中各随机抽取一场的得分,求甲的得分大于乙的得分的概率.
19.(本小题满分12分)
已知等腰直角三角形,其中∠=90 ,.点、分别是、的中点,现将△沿着边折起到△位置,使⊥,连结、.
(Ⅰ)求证:⊥;
(Ⅱ)求二面角的余弦值.
20.(本小题满分12分)
设椭圆的离心率,右焦点到直线的距离为坐标原点.
(Ⅰ)求椭圆的方程;
(II)过点作两条互相垂直的射线,与椭圆分别交于两点,证明:点到直线的距离为定值,并求弦长度的最小值.
21.(本小题满分12分)
已知函数(为常数),直线l与函数的图象都相切,且l与函数的图象的切点的横坐标为l.
(Ⅰ)求直线l的方程及a的值;
(Ⅱ)当k>0时,试讨论方程的解的个数.
请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.
22.(本小题满分10分)
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.
(Ⅰ)求证:△ABE≌△ACD;
(Ⅱ)若AB=6,BC=4,求AE.
23.(本小题满分10分)
已知函数.
(Ⅰ)解不等式≤4;
(Ⅱ)若存在x使得≤0成立,求实数a的取值范围.
24.(本小题满分10分)
已知直线l经过点P(1,1),倾斜角.
(Ⅰ)写出直线l的参数方程
(Ⅱ)设l与圆x2+y2=4相交与两点A、B,求点P到A、B两点的距离之积.
参考答案
18.解:(Ⅰ)运动员甲得分的中位数是22,运动员乙得分的中位数是23………2分
(Ⅱ)…………………3分
…………………4分
…………………………………………………………………………………5分 ……………………………………………………………………………………………6分
,从而甲运动员的成绩更稳定………………………………7分
(Ⅲ)从甲、乙两位运动员的7场得分中各随机抽取一场的得分的基本事件总数为49
……8分
∵ ,
∴ ⊥平面. …… 4分
∵ 平面,
∴ . …… 6分
(Ⅱ)建立如图所示的空间直角坐标系.
则(-1,0,0),(-2,1,0),
(0,0,1).∴=(-1,1,0),
=(1,0,1), ……8分
设平面的法向量为,则
∴ 二面角的余弦值是. ………………12分
20.解:(I)由
由右焦点到直线的距离为
即
即弦AB的长度的最小值是 …………13分
21.解:(1)
比较①和②的系数得。
(2)
-1 (-1,0) 0 (0,1) 1
+ 0 - 0 + 0 -
↗ 极大值ln2 ↘ 极小值 ↗ 极大值ln2 ↘
由函数在R上各区间上的增减及极值情况,可得
(1)当时有两个解;
(2)当时有3个解;
(3)当时有4个解
(4)当k=ln2时有2个解;
(5)当时无解。
22.(本小题满分10分)选修4-1:几何证明选讲
解:(Ⅰ)在ΔABE和ΔACD中,
∵ ∠ABE=∠ACD………………2分
又,∠BAE=∠EDC
∵BD//MN
∴∠EDC=∠DCN
∵直线是圆的切线,
∴∠DCN=∠CAD
∴∠BAE=∠CAD
(2)把直线代入
得
2,4,6
1
2
3
2
3
3
7
1
0
1
4
7
5
4
2
3
2
甲
乙
(第19题图)
②③②
①③②
同课章节目录
