2021年高考物理复习热学课件(共35张PPT)
文档属性
| 名称 | 2021年高考物理复习热学课件(共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-29 09:07:14 | ||
图片预览











文档简介
(共35张PPT)
要点一 分子动理论 内能
[突破指南]
1.分子动能、分子势能和物体的内能
分子动能
分子势能
内能
定义
分子无规则运动的动能(即热运动)
分子间有作用力,由分子间相对位置决定的势能
物体中所有分子的热运动的动能和分子势能的总和
高考专题复习
热学
影响
因素
微观
分子运动的快慢
分子相对位置,分子力
分子动能与分子势能之和
宏观
温度
体积
温度、体积、物质的量
改变方式
升高或降低温度
增大或减小体积
做功和热传递(二者本质不一样)
2.巧用图象理解分子力与分子势能
(1)分子间同时存在引力和斥力,斥力随分子间距离变化比引力快,分子力随分子间距离变化的关系如图甲所示,当分子间距离的数量级大于10-9m时,分子间的作用力可忽略不计.
(2)分子势能与分子间距离的关系如图乙所示,当分子间距离r=r0时,分子力为0,分子势能最小.
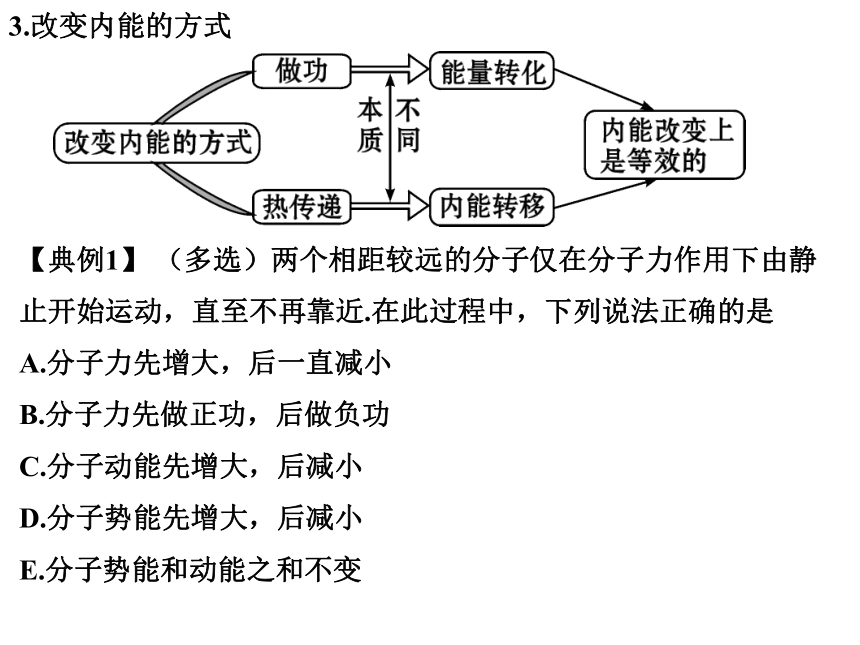
3.改变内能的方式
【典例1】
(多选)两个相距较远的分子仅在分子力作用下由静止开始运动,直至不再靠近.在此过程中,下列说法正确的是
A.分子力先增大,后一直减小
B.分子力先做正功,后做负功
C.分子动能先增大,后减小
D.分子势能先增大,后减小
E.分子势能和动能之和不变
解析 本题考查分子力、分子力做功和分子势能,意在考查考生对分子力、分子力做功与分子势能关系的掌握情况.分子力应先增大,后减小,再增大,所以A选项错误;分子力先为引力,做正功,再为斥力,做负功,B选项正确;根据动能定理可知分子动能先增大后减小,分子势能先减小后增大,分子动能和分子势能之和保持不变,所以C、E选项正确,D错误.
答案 BCE
【借题发挥】
判断分子势能变化的两种方法
方法一:根据分子力做功判断:分子力做正功,分子势能减小;分子力做负功,分子势能增加.
方法二:利用分子势能与分子间距离的关系图线判断.如图所示.
【典例2】
(2015·吉林普通高中摸底)空调在制冷过程中,室内空气中的水蒸气接触蒸发器(铜管)液化成水,经排水管排走,空气中水分越来越少,人会感觉干燥.某空调工作一段时间后,排出液化水的体积V=1.0×103
cm3.已知水的密度ρ=1.0×103
kg/m3、摩尔质量M=1.8×10-2
kg/mol,阿伏加德罗常数NA=6.0×
1023
mol-1.试求:(结果均保留一位有效数字)
(1)该液化水中含有水分子的总数N;
(2)一个水分子的直径d.
答案 (1)3×1025个 (2)4×10-10
m
要点三 热力学定律的理解与应用
[突破指南]
1.对热力学第一定律的理解
(1)热力学第一定律不仅反映了做功和热传递这两种方式改变内能的过程是等效的,而且给出了内能的变化量和做功与热传递之间的定量关系,即ΔU=Q+W.
(2)几种特殊情况
①若过程是绝热的,则Q=0,W=ΔU,外界对物体做的功等于物体内能的增加量.
②若过程中不做功,即W=0,则Q=ΔU,物体吸收的热量等于物体内能的增加量.
③若过程的始、末状态物体的内能不变,即ΔU=0,则W+Q=0或W=-Q.外界对物体做的功等于物体放出的热量.
2.对热力学第二定律的理解
(1)在热力学第二定律的表述中,“自发地”、“不产生其他影响”的涵义.
①“自发地”指明了热传递等热力学宏观现象的方向性,不需要借助外界提供能量的帮助.
②“不产生其他影响”的涵义是发生的热力学宏观过程只在本系统内完成,对周围环境不产生热力学方面的影响.如吸热、放热、做功等.
(2)热力学第二定律的实质
热力学第二定律的每一种表述,都揭示了大量分子参与宏观过程的方向性,进而使人们认识到自然界中进行的涉及热现象的宏观过程都具有方向性.
(3)热力学过程的方向性实例
(4)两类永动机的比较
分类
第一类永动机
第二类永动机
设计要求
不需要任何动力或燃料,却能不断地对外做功的机器
从单一热源吸收热量,使之完全变成功,而不产生其他影响的机器
不可能制成的原因
违背能量守恒
不违背能量守恒,违背热力学第二定律
【典例3】
(多选)关于热力学定律,下列说法正确的是 .
A.为了增加物体的内能,必须对物体做功或向它传递热量
B.对某物体做功,必定会使该物体的内能增加
C.可以从单一热源吸收热量,使之完全变为功
D.不可能使热量从低温物体传向高温物体
E.功转变为热的实际宏观过程是不可逆过程
解析 由ΔU=W+Q可知做功和热传递是改变内能的两种途径.它们具有等效性,故A正确、B错误.由热力学第二定律可知,可以从单一热源吸收热量,使之全部变为功.但会产生其他影响,故C正确.同样热量只是不能自发地从低温物体传向高温物体,则D项错.一切与热现象有关的宏观过程不可逆,则E正确.
ACE
要点四 气体压强的计算
[突破指南]
1.液体封闭的气体压强的确定
(1)平衡法:选与气体接触的液柱为研究对象进行受力分析,利用它的受力平衡,求出气体的压强.
(2)取等压面法:根据同种液体在同一水平液面处压强相等,在连通器内灵活选取等压面,由两侧压强相等建立方程求出压强.液体内部深度为h处的总压强p=p0+ρgh,式中p0为液面上方大气压强.在水银内用cmHg作单位时可表示为p=h0+h.
2.固体(活塞或汽缸)封闭的气体压强的确定
由于该固体必定受到被封闭气体的压力,可通过对该固体进行受力分析,由平衡条件建立方程来找出气体压强与其他各力的关系.
【典例4】
如图所示,一汽缸水平固定在静止的小车上,一质量为m,面积为S的活塞将一定量的气体封闭在汽缸内,平衡时活塞与汽缸底相距L.现让小车以一较小的水平恒定加速度向右运动,稳定时发现活塞相对于汽缸移动了距离d.已知大气压强为p0,不计汽缸和活塞间的摩擦;且小车运动时,大气对活塞的压强仍可视为p0;整个过程温度保持不变.求小车加速度的大小.
【借题发挥】
求解气体压强的技巧
求封闭气体压强时,若较简单的平衡类问题,可直接列压强平衡方程式;若较复杂的平衡类或非平衡类问题,一般选取活塞或水银柱进行受力分析,列牛顿第二定律的方程进行求解.
要点五 气体实验定律及状态方程的应用
[突破指南]
利用气体实验定律及气态方程解决问题的基本思路
【典例5】
如图所示,由U型管和细管连接的玻璃泡A、B和C浸泡在温度均为0
℃的水槽中,B的容积是A的3倍.阀门S将A和B两部分隔开.A内为真空,B和C内都充有气体.U型管内左边水银柱比右边的低60
mm.打开阀门S,整个系统稳定后,U型管内左、右水银柱高度相等.假设U型管和细管中的气体体积远小于玻璃泡的容积.
(1)求玻璃泡C中气体的压强(以mmHg为单位);
(2)将右侧水槽的水从0
℃加热到一定温度时,U型管内左、右水银柱高度差又为60
mm,求加热后右侧水槽的水温.
答案 (1)180
mmHg (2)364
K
【借题发挥】
分析气体状态变化的问题要抓住三点
(1)阶段性:即弄清一个物理过程分为哪几个阶段.
(2)联系性:即找出几个阶段之间是由什么物理量联系起来的.
(3)规律性:即明确哪个阶段应遵循什么实验定律.
要点六 气体实验定律与热力学第一定律的综合
[突破指南]
【典例6】
如图所示,粗细均匀、导热良好、装有适量水银的U形管竖直放置,右端与大气相通,左端封闭气柱长l1=20
cm(可视为理想气体),两管中水银面等高.现将右端与一低压舱(未画出)接通,稳定后右管水银面高出左管水银面h=10
cm.(环境温度不变,大气压强p0=75
cm
Hg)
(1)求稳定后低压舱内的压强(用“cm
Hg”作单位).
(2)此过程中左管内的气体对外界 (选填“做正功”“做负功”或“不做功”),气体将 (选填“吸热”或“放热”).
【解题探究】
(1)封闭气体发生什么变化?可利用什么定律求解?
(2)粗细均匀的U形管一侧液面下降h时,两侧液面的高度差为多少?
(3)理想气体的内能与什么有关?
提示 (1)等温变化.利用玻意耳定律求解.
(2)高度差为2h.
(3)与温度有关.
解析 (1)设U形管横截面积为S,右端与大气相通时,左管中封闭气体的压强为p1,右端与一低压舱接通后,左管中封闭气体的压强为p2,气柱长度为l2,稳定后低压舱内的压强为p.高为h的水银柱产生的压强为ph.
左管中封闭气体发生等温变化,根据玻意耳定律得
p1V1=p2V2①
p1=p0
②
p2=p+ph③
V1=l1S④
V2=l2S⑤
由几何关系得h=2(l2-l1)⑥
联立①②③④⑤⑥式,代入数据得p=50
cm
Hg
(2)此过程中由于左管中的气体的体积变大.故左管内的气体对外界做正功;由于U形管导热良好,故此过程中,左管中的气体做等温变化,气体的内能变化为零,由热力学第一定律W+Q=ΔU可知W<0,ΔU=0,故Q>0,即气体将吸热.
答案 (1)50
cm
Hg (2)做正功 吸热
变质量气体问题的分析技巧
分析变质量问题时,可通过巧妙地选择研究对象,使这类问题转化为一定质量的气体问题,用气体实验定律求解.
(1)打气问题:向球、轮胎中充气是一个典型的变质量的气体问题,只要选择球内原有气体和即将充入的气体作为研究对象,就可把充气过程中的气体质量变化问题转化为定质量气体的状态变化问题.
(2)抽气问题:从容器内抽气的过程中,容器内的气体质量不断减小,这属于变质量问题.分析时,将每次抽气过程中抽出的气体和剩余气体作为研究对象,质量不变,故抽气过程可以看做是等温膨胀过程.
(3)灌气问题:将一个大容器里的气体分装到多个小容器中的问题也是一个典型的变质量问题.分析这类问题时,把大容器中的剩余气体和多个小容器中的气体视为整体作为研究对象,可将变质量问题转化为定质量问题.
(4)漏气问题:容器漏气过程中气体的质量不断发生变化,属于变质量问题.如果选容器内剩余气体和漏出气体整体作为研究对象,便可使问题变成一定质量气体的状态变化,可用理想气体的状态方程求解.
【典例1】
一太阳能空气集热器,底面及侧面为隔热材料,顶面为透明玻璃板,集热器容积为V0,开始时内部封闭气体的压强为p0.经过太阳曝晒,气体温度由T0=300
K升至T1=350
K.
(1)求此时气体的压强;
(2)保持T1=350
K不变,缓慢抽出部分气体,使气体压强再变回到p0.求集热器内剩余气体的质量与原来总质量的比值.判断在抽气过程中剩余气体是吸热还是放热,并简述原因.
因为抽气过程中剩余气体温度不变,故内能不变,而剩余气体的体积膨胀对
外做功.由热力学第一定律ΔU=W+Q可知,气体一定从外界吸收热量.
【典例2】
(2015·河南郑州一中期中)用真空泵抽出某容器中的空气,若某容器的容积为V,真空泵一次抽出空气的体积为V0,设抽气时气体温度不变,容器里原来的空气压强为p,求抽出n次空气后容器中空气的压强是多少?
要点一 分子动理论 内能
[突破指南]
1.分子动能、分子势能和物体的内能
分子动能
分子势能
内能
定义
分子无规则运动的动能(即热运动)
分子间有作用力,由分子间相对位置决定的势能
物体中所有分子的热运动的动能和分子势能的总和
高考专题复习
热学
影响
因素
微观
分子运动的快慢
分子相对位置,分子力
分子动能与分子势能之和
宏观
温度
体积
温度、体积、物质的量
改变方式
升高或降低温度
增大或减小体积
做功和热传递(二者本质不一样)
2.巧用图象理解分子力与分子势能
(1)分子间同时存在引力和斥力,斥力随分子间距离变化比引力快,分子力随分子间距离变化的关系如图甲所示,当分子间距离的数量级大于10-9m时,分子间的作用力可忽略不计.
(2)分子势能与分子间距离的关系如图乙所示,当分子间距离r=r0时,分子力为0,分子势能最小.
3.改变内能的方式
【典例1】
(多选)两个相距较远的分子仅在分子力作用下由静止开始运动,直至不再靠近.在此过程中,下列说法正确的是
A.分子力先增大,后一直减小
B.分子力先做正功,后做负功
C.分子动能先增大,后减小
D.分子势能先增大,后减小
E.分子势能和动能之和不变
解析 本题考查分子力、分子力做功和分子势能,意在考查考生对分子力、分子力做功与分子势能关系的掌握情况.分子力应先增大,后减小,再增大,所以A选项错误;分子力先为引力,做正功,再为斥力,做负功,B选项正确;根据动能定理可知分子动能先增大后减小,分子势能先减小后增大,分子动能和分子势能之和保持不变,所以C、E选项正确,D错误.
答案 BCE
【借题发挥】
判断分子势能变化的两种方法
方法一:根据分子力做功判断:分子力做正功,分子势能减小;分子力做负功,分子势能增加.
方法二:利用分子势能与分子间距离的关系图线判断.如图所示.
【典例2】
(2015·吉林普通高中摸底)空调在制冷过程中,室内空气中的水蒸气接触蒸发器(铜管)液化成水,经排水管排走,空气中水分越来越少,人会感觉干燥.某空调工作一段时间后,排出液化水的体积V=1.0×103
cm3.已知水的密度ρ=1.0×103
kg/m3、摩尔质量M=1.8×10-2
kg/mol,阿伏加德罗常数NA=6.0×
1023
mol-1.试求:(结果均保留一位有效数字)
(1)该液化水中含有水分子的总数N;
(2)一个水分子的直径d.
答案 (1)3×1025个 (2)4×10-10
m
要点三 热力学定律的理解与应用
[突破指南]
1.对热力学第一定律的理解
(1)热力学第一定律不仅反映了做功和热传递这两种方式改变内能的过程是等效的,而且给出了内能的变化量和做功与热传递之间的定量关系,即ΔU=Q+W.
(2)几种特殊情况
①若过程是绝热的,则Q=0,W=ΔU,外界对物体做的功等于物体内能的增加量.
②若过程中不做功,即W=0,则Q=ΔU,物体吸收的热量等于物体内能的增加量.
③若过程的始、末状态物体的内能不变,即ΔU=0,则W+Q=0或W=-Q.外界对物体做的功等于物体放出的热量.
2.对热力学第二定律的理解
(1)在热力学第二定律的表述中,“自发地”、“不产生其他影响”的涵义.
①“自发地”指明了热传递等热力学宏观现象的方向性,不需要借助外界提供能量的帮助.
②“不产生其他影响”的涵义是发生的热力学宏观过程只在本系统内完成,对周围环境不产生热力学方面的影响.如吸热、放热、做功等.
(2)热力学第二定律的实质
热力学第二定律的每一种表述,都揭示了大量分子参与宏观过程的方向性,进而使人们认识到自然界中进行的涉及热现象的宏观过程都具有方向性.
(3)热力学过程的方向性实例
(4)两类永动机的比较
分类
第一类永动机
第二类永动机
设计要求
不需要任何动力或燃料,却能不断地对外做功的机器
从单一热源吸收热量,使之完全变成功,而不产生其他影响的机器
不可能制成的原因
违背能量守恒
不违背能量守恒,违背热力学第二定律
【典例3】
(多选)关于热力学定律,下列说法正确的是 .
A.为了增加物体的内能,必须对物体做功或向它传递热量
B.对某物体做功,必定会使该物体的内能增加
C.可以从单一热源吸收热量,使之完全变为功
D.不可能使热量从低温物体传向高温物体
E.功转变为热的实际宏观过程是不可逆过程
解析 由ΔU=W+Q可知做功和热传递是改变内能的两种途径.它们具有等效性,故A正确、B错误.由热力学第二定律可知,可以从单一热源吸收热量,使之全部变为功.但会产生其他影响,故C正确.同样热量只是不能自发地从低温物体传向高温物体,则D项错.一切与热现象有关的宏观过程不可逆,则E正确.
ACE
要点四 气体压强的计算
[突破指南]
1.液体封闭的气体压强的确定
(1)平衡法:选与气体接触的液柱为研究对象进行受力分析,利用它的受力平衡,求出气体的压强.
(2)取等压面法:根据同种液体在同一水平液面处压强相等,在连通器内灵活选取等压面,由两侧压强相等建立方程求出压强.液体内部深度为h处的总压强p=p0+ρgh,式中p0为液面上方大气压强.在水银内用cmHg作单位时可表示为p=h0+h.
2.固体(活塞或汽缸)封闭的气体压强的确定
由于该固体必定受到被封闭气体的压力,可通过对该固体进行受力分析,由平衡条件建立方程来找出气体压强与其他各力的关系.
【典例4】
如图所示,一汽缸水平固定在静止的小车上,一质量为m,面积为S的活塞将一定量的气体封闭在汽缸内,平衡时活塞与汽缸底相距L.现让小车以一较小的水平恒定加速度向右运动,稳定时发现活塞相对于汽缸移动了距离d.已知大气压强为p0,不计汽缸和活塞间的摩擦;且小车运动时,大气对活塞的压强仍可视为p0;整个过程温度保持不变.求小车加速度的大小.
【借题发挥】
求解气体压强的技巧
求封闭气体压强时,若较简单的平衡类问题,可直接列压强平衡方程式;若较复杂的平衡类或非平衡类问题,一般选取活塞或水银柱进行受力分析,列牛顿第二定律的方程进行求解.
要点五 气体实验定律及状态方程的应用
[突破指南]
利用气体实验定律及气态方程解决问题的基本思路
【典例5】
如图所示,由U型管和细管连接的玻璃泡A、B和C浸泡在温度均为0
℃的水槽中,B的容积是A的3倍.阀门S将A和B两部分隔开.A内为真空,B和C内都充有气体.U型管内左边水银柱比右边的低60
mm.打开阀门S,整个系统稳定后,U型管内左、右水银柱高度相等.假设U型管和细管中的气体体积远小于玻璃泡的容积.
(1)求玻璃泡C中气体的压强(以mmHg为单位);
(2)将右侧水槽的水从0
℃加热到一定温度时,U型管内左、右水银柱高度差又为60
mm,求加热后右侧水槽的水温.
答案 (1)180
mmHg (2)364
K
【借题发挥】
分析气体状态变化的问题要抓住三点
(1)阶段性:即弄清一个物理过程分为哪几个阶段.
(2)联系性:即找出几个阶段之间是由什么物理量联系起来的.
(3)规律性:即明确哪个阶段应遵循什么实验定律.
要点六 气体实验定律与热力学第一定律的综合
[突破指南]
【典例6】
如图所示,粗细均匀、导热良好、装有适量水银的U形管竖直放置,右端与大气相通,左端封闭气柱长l1=20
cm(可视为理想气体),两管中水银面等高.现将右端与一低压舱(未画出)接通,稳定后右管水银面高出左管水银面h=10
cm.(环境温度不变,大气压强p0=75
cm
Hg)
(1)求稳定后低压舱内的压强(用“cm
Hg”作单位).
(2)此过程中左管内的气体对外界 (选填“做正功”“做负功”或“不做功”),气体将 (选填“吸热”或“放热”).
【解题探究】
(1)封闭气体发生什么变化?可利用什么定律求解?
(2)粗细均匀的U形管一侧液面下降h时,两侧液面的高度差为多少?
(3)理想气体的内能与什么有关?
提示 (1)等温变化.利用玻意耳定律求解.
(2)高度差为2h.
(3)与温度有关.
解析 (1)设U形管横截面积为S,右端与大气相通时,左管中封闭气体的压强为p1,右端与一低压舱接通后,左管中封闭气体的压强为p2,气柱长度为l2,稳定后低压舱内的压强为p.高为h的水银柱产生的压强为ph.
左管中封闭气体发生等温变化,根据玻意耳定律得
p1V1=p2V2①
p1=p0
②
p2=p+ph③
V1=l1S④
V2=l2S⑤
由几何关系得h=2(l2-l1)⑥
联立①②③④⑤⑥式,代入数据得p=50
cm
Hg
(2)此过程中由于左管中的气体的体积变大.故左管内的气体对外界做正功;由于U形管导热良好,故此过程中,左管中的气体做等温变化,气体的内能变化为零,由热力学第一定律W+Q=ΔU可知W<0,ΔU=0,故Q>0,即气体将吸热.
答案 (1)50
cm
Hg (2)做正功 吸热
变质量气体问题的分析技巧
分析变质量问题时,可通过巧妙地选择研究对象,使这类问题转化为一定质量的气体问题,用气体实验定律求解.
(1)打气问题:向球、轮胎中充气是一个典型的变质量的气体问题,只要选择球内原有气体和即将充入的气体作为研究对象,就可把充气过程中的气体质量变化问题转化为定质量气体的状态变化问题.
(2)抽气问题:从容器内抽气的过程中,容器内的气体质量不断减小,这属于变质量问题.分析时,将每次抽气过程中抽出的气体和剩余气体作为研究对象,质量不变,故抽气过程可以看做是等温膨胀过程.
(3)灌气问题:将一个大容器里的气体分装到多个小容器中的问题也是一个典型的变质量问题.分析这类问题时,把大容器中的剩余气体和多个小容器中的气体视为整体作为研究对象,可将变质量问题转化为定质量问题.
(4)漏气问题:容器漏气过程中气体的质量不断发生变化,属于变质量问题.如果选容器内剩余气体和漏出气体整体作为研究对象,便可使问题变成一定质量气体的状态变化,可用理想气体的状态方程求解.
【典例1】
一太阳能空气集热器,底面及侧面为隔热材料,顶面为透明玻璃板,集热器容积为V0,开始时内部封闭气体的压强为p0.经过太阳曝晒,气体温度由T0=300
K升至T1=350
K.
(1)求此时气体的压强;
(2)保持T1=350
K不变,缓慢抽出部分气体,使气体压强再变回到p0.求集热器内剩余气体的质量与原来总质量的比值.判断在抽气过程中剩余气体是吸热还是放热,并简述原因.
因为抽气过程中剩余气体温度不变,故内能不变,而剩余气体的体积膨胀对
外做功.由热力学第一定律ΔU=W+Q可知,气体一定从外界吸收热量.
【典例2】
(2015·河南郑州一中期中)用真空泵抽出某容器中的空气,若某容器的容积为V,真空泵一次抽出空气的体积为V0,设抽气时气体温度不变,容器里原来的空气压强为p,求抽出n次空气后容器中空气的压强是多少?
同课章节目录
