浙江省宁波市初中数学几何模型汇总版(Word版,附答案)
文档属性
| 名称 | 浙江省宁波市初中数学几何模型汇总版(Word版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 11:15:35 | ||
图片预览




文档简介
目录
TOC
\o
"1-3"
\h
\u
8字模型与飞镖模型
2
角平分线四大模型
11
截长补短辅助线模型
21
手拉手模型
29
三垂直全等模型
36
中考复习专题(将军饮马问题题型归纳)
45
蚂蚁行程
51
中点四大模型
59
半角模型
75
相似模型
82
圆中的辅助线
109
第十二章
辅助圆
120
几何秘籍
8字模型与飞镖模型
模型1:角的8字模型
如图所示,AC、BD相交于点O,连接AD、BC.
结论:∠A+∠D=∠B+∠C.
模型分析
证法一:
∵∠AOB是△AOD的外角,∴∠A+∠D=∠AOB.∵∠AOB是△BOC的外角,
∴∠B+∠C=∠AOB.∴∠A+∠D=∠B+∠C.
证法二:
∵∠A+∠D+∠AOD=180°,∴∠A+∠D=180°-∠AOD.∵∠B+∠C+∠BOC=180°,
∴∠B+∠C=180°-∠BOC.又∵∠AOD=∠BOC,∴∠A+∠D=∠B+∠C.
(1)因为这个图形像数字8,所以我们往往把这个模型称为8字模型.
(2)8字模型往往在几何综合题目中推导角度时用到.
模型实例
观察下列图形,计算角度:
(1)如图①,∠A+∠B+∠C+∠D+∠E=________;
解法一:利用角的8字模型.如图③,连接CD.∵∠BOC是△BOE的外角,
∴∠B+∠E=∠BOC.∵∠BOC是△COD的外角,∴∠1+∠2=∠BOC.
∴∠B+∠E=∠1+∠2.(角的8字模型),∴∠A+∠B+∠ACE+∠ADB+∠E
=∠A+∠ACE+∠ADB+∠1+∠2=∠A+∠ACD+∠ADC=180°.
解法二:如图④,利用三角形外角和定理.∵∠1是△FCE的外角,∴∠1=∠C+∠E.
∵∠2是△GBD的外角,∴∠2=∠B+∠D.
∴∠A+∠B+∠C+∠D+∠E=∠A+∠1+∠2=180°.
(2)如图②,∠A+∠B+∠C+∠D+∠E+∠F=________.
(2)解法一:
如图⑤,利用角的8字模型.∵∠AOP是△AOB的外角,∴∠A+∠B=∠AOP.
∵∠AOP是△OPQ的外角,∴∠1+∠3=∠AOP.∴∠A+∠B=∠1+∠3.①(角的8字模型),同理可证:∠C+∠D=∠1+∠2.②
,∠E+∠F=∠2+∠3.③
由①+②+③得:∠A+∠B+∠C+∠D+∠E+∠F=2(∠1+∠2+∠3)=360°.
解法二:利用角的8字模型.如图⑥,连接DE.∵∠AOE是△AOB的外角,
∴∠A+∠B=∠AOE.∵∠AOE是△OED的外角,∴∠1+∠2=∠AOE.
∴∠A+∠B=∠1+∠2.(角的8字模型)
∴∠A+∠B+∠C+∠ADC+∠FEB+∠F=∠1+∠2+∠C+∠ADC+∠FEB+∠F
=360°.(四边形内角和为360°)
练习:
1.(1)如图①,求:∠CAD+∠B+∠C+∠D+∠E=
;
解:如图,∵∠1=∠B+∠D,∠2=∠C+∠CAD,
∴∠CAD+∠B+∠C+∠D+∠E=∠1+∠2+∠E=180°.
故答案为:180°
解法二:
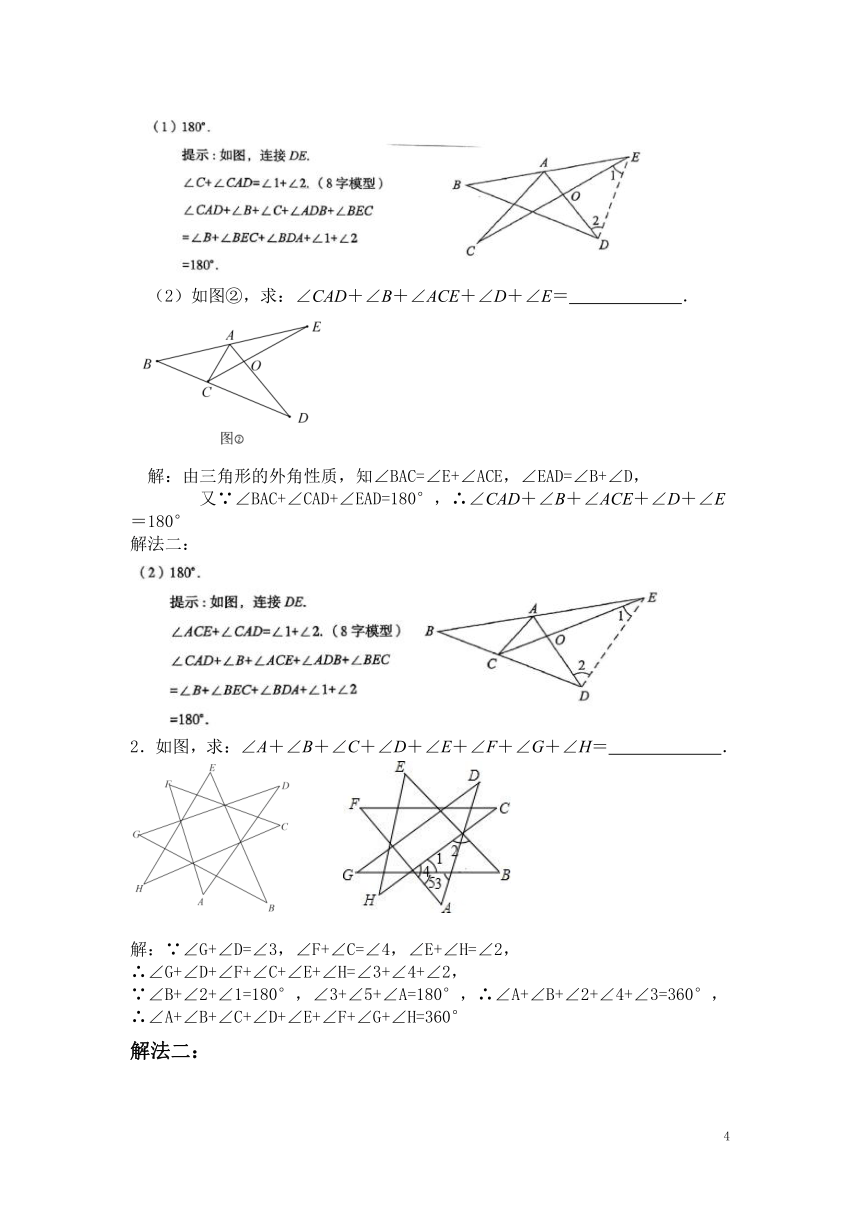
(2)如图②,求:∠CAD+∠B+∠ACE+∠D+∠E=
.
解:由三角形的外角性质,知∠BAC=∠E+∠ACE,∠EAD=∠B+∠D,
又∵∠BAC+∠CAD+∠EAD=180°,∴∠CAD+∠B+∠ACE+∠D+∠E=180°
解法二:
2.如图,求:∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=
.
解:∵∠G+∠D=∠3,∠F+∠C=∠4,∠E+∠H=∠2,∴∠G+∠D+∠F+∠C+∠E+∠H=∠3+∠4+∠2,
∵∠B+∠2+∠1=180°,∠3+∠5+∠A=180°,∴∠A+∠B+∠2+∠4+∠3=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°
解法二:
模型2:角的飞镖模型
如图所示,有结论:∠D=∠A+∠B+∠C.
模型分析
解法一:如图①,作射线AD.
∵∠3是△ABD的外角,∴∠3=∠B+∠1,∵∠4是△ACD的外角,∴∠4=∠C+∠2
∴∠BDC=∠3+∠4,∴∠BDC=∠B+∠1+∠2+∠C,∴∠BDC=∠BAC+∠B+∠C
解法二:如图②,连接BC.
∵∠2+∠4+∠D=180°,∴∠D=180°-(∠2+∠4)
∵∠1+∠2+∠3+∠4+∠A=180°,∴∠A+∠1+∠3=180°-(∠2+∠4)
∴∠D=∠A+∠1+∠3.
(1)因为这个图形像飞镖,所以我们往往把这个模型称为飞镖模型.
(2)飞镖模型在几何综合题目中推导角度时使用.
模型实例
如图,在四边形ABCD中,AM、CM分别平分∠DAB和∠DCB,AM与CM交于M,探究∠AMC与∠B、∠D间的数量关系.
解答:利用角的飞镖模型
如图所示,连接DM并延长.∵∠3是△AMD的外角,∴∠3=∠1+∠ADM,
∵∠4是△CMD的外角,∴∠4=∠2+∠CDM,∵∠AMC=∠3+∠4
∴∠AMC=∠1+∠ADM+∠CDM+∠2,∴∠AMC=∠1+∠2+∠ADC.(角的飞镖模型)
∵AM、CM分别平分∠DAB和∠DCB,∴,,
∴,∴(四边形内角和360°),∴,∴2∠AMC+∠B-∠ADC=360°.
练习:
1.如图,求∠A+∠B+∠C+∠D+∠E+∠F=
.
【答案】230°
提示:∠C+∠E+∠D=∠EOC=115?.(飞镖模型),∠A+∠B+∠F=∠BOF=115?.
∠A+∠B+∠C+∠D+∠E+∠F=115?+115?=230?
2.如图,求∠A+∠B+∠C+∠D=
.
【答案】220°
提示:如图所示,连接BD.
∠AED=∠A+∠3+∠1,∠BFC=∠2+∠4+∠C,
∠A+∠ABF+∠C+∠CDE=∠A+∠3+∠1+∠2+∠4+∠C=∠AED+∠BFC=220?
模型3
边的“8”字模型
如图所示,AC、BD相交于点O,连接AD、BC.结论AC+BD>AD+BC.
模型分析
∵OA+OD>AD①,
OB+OC>BC②,
由①+②得:
OA+OD+OB+OC>BC+AD
即:AC+BD>AD+BC.
模型实例
如图,四边形ABCD的对角线AC、BD相交于点O。
求证:(1)
AB+BC+CD+AD>AC+BD;
(2)
AB+BC+CD+AD
<2AC+2BD.
证明:(1)∵AB+BC>AC①,
CD+AD>AC②,
AB+AD>BD③,
BC+CD>
BD④
由①+②+③+④得:
2
(AB+BC+CD+AD)>2(AC+BD).
即AB+BC+CD+AD
>AC+BD.
(2)
∵AD,BC由①+②得:
AD+BC<
OA+OD+OB+OC.
∴AD+BC同理可证:AB+CD
∴AB+BC+CD+AD<
2AC+2BD.
模型4
边的飞镖模型
如图所示有结论:AB+AC>
BD+CD.
模型分析
如图,延长BD交AC于点E。
∵AB+AC=AB+AE+EC,AB+AE>BE,∴AB+A
C>BE+EC.①
,∵BE+EC=BD+DE+EC,
DE+EC>
CD,∴BE+EC>BD+CD.
②
,由①②可得:AB+AC>BD+CD.
模型实例
如图,点O为三角形内部一点.
求证:(1)
2
(AO+BO+CO)>AB+BC+AC;
(2)
AB+BC+AC>AO+BO+CO.
证明:(1)∵OA+OB>AB①,
OB+OC>BC②,
OC+OA>AC③
由①+②+③得:
2
(AO+BO+CO)>AB+BC+AC
(2)如图,延长BO交AC于点E,
∵AB+AC=AB+AE+EC,
AB+AE>BE,
∴AB+AC>BE+EC.
①
∵BE+EC=BO+OE+EC,
OE+EC>CO,∴BE+EC>BO+CO,②
由①②可得:
AB+AC>BO+CO.③(边的飞镖模型)
同理可得:
AB+BC>OA+OC.④
,BC+AC>OA+OB.⑤
由③+④+⑤得:
2
(AB+BC+AC)>2
(AO+BO+CO).
即
AB+BC+AC>AO+BO+CO.
1.如图,在△ABC中,D、E在BC边上,且BD=CE。求证:AB+AC>AD+AE.
【答案】
证法一:如图①,将AC平移至BF,AD延长线与BF相交于点G,连接DF。
由平移可得AC=BF
,∵AC∥BF
,∴∠ACE=∠BFD
,∵BD=CE
∴△AEC≌△FDB
,∴DF=AE
如图,延长AD交BF于点G,∵AB+BF=AB+BG+GF.
∵AB+BG>AG,
∴AB+BF>AG+GF①
,∵AG+GF=AD+DG+GF,
∵DG+GF>DF,
∴AG+GF>AD+DF②
,由①②可得:AB+BF>AD+DF.(飞镖模型)
∴AB+AC=AB+BF>AD+DF=AD+AE.
∴AB+AC>AD+AE.
证法二:如图②,将AC平移至DF,连接BF
,则AC=DF
,∵AC∥DF,∴∠ACE=∠FDB.
∵BD=CE,∴△AEC≌△FBD.
∴BF=AE.
∵OA+OD>AD①,
OB+OF>BF②
由①+②得:OA+OD+OB+OF>BF+AD.
∴AB+DF>BF+AD.(8字模型)
∴AB+AC=AB+DF>BF+AD=AE+AD.
∴AB+AC>AD+AE.
2.观察图形并探究下列各问题,写出你所观察得到的结论,并说明理由.
(1)如图①,△ABC中,P为边BC一点,请比较BP+PC与AB+AC的大小,并说明理由.
(2)如图②,将(1)中的点P移至△ABC内,请比较△BPC的周长与△ABC的周长的大小,并说明理由.
(3)图③将(2)中的点P变为两个点、,请比较四边形的周长与△ABC的周长的大小,并说明理由.
【答案】
(1)如图①,BP+PC理由:三角形两边之和大于第三边。(或两点之间线段最短)
(2)△BPC的周长小于△ABC的周长。
证明:如图②,延长BP交AC于M。在△ABM中,BP+PM在△PMC中,PC,由①+②得:BP+PC∴△BPC的周长小于△ABC的周长。
(3)四边形的周长小于△ABC的周长。
证法一:如图③,分别延长、交于M,由(2)知,BM+CM又∵<,∴++∴四边形的周长小于△ABC的周长.
证法二:如图④,做直线分别交AB、AC于M、N。在△BM中,在△AMN中,++,在△中,<+NC③
由①+②+③得:∴++∴四边形的周长小于△ABC的周长.
角平分线四大模型
模型1
角平分线的点向两边作垂线
如图,P是∠MON的平分线上一点,过点P作PA⊥OM于点A,PB⊥ON于点B,则PB=PA
模型分析
利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口
模型实例
(1)如图①,在△ABC中,∠C=90°,AD平分∠CAB,BC=6,BD=4,那么点D到直线AB的距离是
解答:如图,过点D作DE⊥AB于点E,∵AD平分∠CAB,∴CD=DE.
∵CB=6,BD=4,∴DE=CD=2,即点D到直线AB的距离是2.
(2)如图②,∠1=∠2,∠3=∠4,求证:AP平分∠BAC
证明:如图,过点P作PD⊥AB于点D,PE⊥BC于点E,PF⊥AC于点F,
∵∠1=∠2,∴PD=PE,∵∠3=∠4,
∴PE=PF,∴PD=PF
又∵PD⊥AB,PF⊥AC,∴AP平分∠BAC(角平分线的判定)
练习
如图,在四边形ABCD中,BC>AB,AD=DC,BD平分∠ABC
,
求证:∠BAD+∠BCD=180°
证明:作DE⊥BC于E,作DF⊥BA的延长线于F,∴∠F=∠DEC=90°,
∵BD平分∠ABC,∴DF=DE,又∵AD=DC,∴△DFA≌DEC,∴∠FAD=∠C
∵∠FAD+∠BAD=180°,∴∠BAD+∠BCD=180°
2.如图,△ABC的外角∠ACD∠的平分线CP与内角∠ABC的平分线BP相交于点P,若∠BPC=40°,则∠CAP=
.
解答:如图所示,作PN⊥BD于N,作PF⊥BA,交BA延长线于F,作PM⊥AC于M
∵BP、CP分别是∠CBA和∠DCA的角平分线,∴∠ABP=∠CBP,∠DCP=∠ACP,
PF=PN=PM,∵∠BAC=∠ACD-∠ABC,∠BPC=∠PCD-∠PBC(外角性质)
∴∠BAC=2∠PCD-2∠PBC=2(∠PCD-∠PBC)=2∠BPC=80°
∴∠CAF=180°-∠BAC=100°,∵PF=PM
∴AP是∠FAC的角平分线,∴∠CAP=∠PAF=50°
模型2
截取构造对称全等
如图,P是∠MON的平分线上的一点,点A是射线OM上任意一点,在ON上截取OB=OA,连接PB,则△OPB≌△OPA
模型分析
利用角平分线图形的对称性,在铁的两边构造对称全等三角形,可以得到对应边,对应角相等,利用对称
性把一些线段或角进行转移,这是经常使用的一种解题技巧
模型实例
(1)如图①所示,在△ABC中,AD是△BAC的外角平分线,P是AD上异于点A的任意一点,试比较PB+PC与AB+AC的大小,并说明理由
解题:PB+PC>AB+AC
证明:在BA的延长线上取点E,
使AE=AB,连接PE,∵AD平分∠CAE
∴∠CAD=∠EAD,在△AEP与△ACP中,∵AE=AB,∠CAD=∠EAD,
AP=AP,∴△AEP≌△ACP
(SAS),∴PE=PC
∵在△PBE中:PB+PE>BE,BE=AB+AE=AB+AC,∴PB+PC>AB+AC
(2)如图②所示,AD是△ABC的内角平分线,其它条件不变,试比较PC-PB与AC-AB的大小,并说明理由
解答:AC-AB>PC-PB
证明:在△ABC中,
在AC上取一点E,使AE=AB
,∴AC-AE=AB-AC=BE
∵AD平分∠BAC
,∴∠EAP=∠BAP
,在△AEP和△ACP中
∴△AEP≌△ABP
(SAS)
,∴PE=PB
,∵在△CPE中
CE>CP-PE
,∴AC-AB>PC-PB
练习
已知,在△ABC中,∠A=2∠B,CD是∠ACB的平分线,AC=16,AD=8,
求线段BC的长
解:如图在BC边上截取CE=AC,连结DE,在△ACD和△ECD中
∴△ACD≌△ECD(SAS)
∴AD=DE
,
∠A=∠1
,∵∠A=2∠B,∴∠1=2∠B,
∵∠1=∠B+∠EDB
,
∴∠B=∠EDB,
∴EBB=ED
,
∴EB=DA=8,BC=EC+BE=AC+DA=16+8=24
在△ABC中,AB=AC,∠A=108°,BD平分∠ABC,
求证:BC=AB+CD
证明:在BC上截取BE=BA,连结DE,∵BD平分∠ABC,BE=AB,BD=BD
∴△ABD≌△EBD(SAS),∴∠DEB=∠A=108°,∴∠DEC=180°-108°=72°
∵AB=AC,∴∠C=∠ABC=(180°-108°)=36°,∴∠EDC=72°
,
∴∠DEC=∠EDC,∴CE=CD
,∴BE+CE=AB+CD,∴BC=AB+CD
3.如图所示,在△ABC中,∠A=100°,∠ABC=40°,BD是∠ABC的平分线,延长BD至E,使DE=AD,求证:BC=AB+CE
证明:在CB上取点F,使得BF=AB,连结DF,∵BD平分∠ABC,BD=BD
∴△ABD≌△FBD,∴DF=AD=DE,∠ADB=∠FDB,∴BD平分∠ABC
∴∠ABD=20°,则∠ADB=180°-20°-100°=60°=∠CDE
∠CDF=180°-∠ADB-∠FDB=60°,∴∠CDF=∠CDE,在△CDE和△CDF中
∴△CDE≌CDF,∴CE=CF,∴BC=BF+FC=AB+CE
模型3
角平分线+垂线构造等腰三角形
如图,P是∠MON的平分线上一点,AP丄OP于P点,延长AP交ON于点.B,则△AOB是等腰三角形.
模型分析
构造此模型可以利用等腰三角形的"三线合一”,也可以得到两个全等的直角三角形.进而得到对应边.对应角相等.这个模型巧妙地把角平分线和三线合一联系了起来.
模型实例
如图.己知等腰直角三角形ABC中,∠A=90°,
AB=AC,
BD平分∠ABC,
C?丄BD.垂足为E.求证:BD=2C?.
解答:如图,延长CE、BA交于点F,∵CE丄BD于E,
∠BAC=90°,∴∠BAD=∠CED.
∴∠ABD=∠ACF.又∵AB=AC,
∠BAD=∠CAF=90°,
∴△ABD≌△ACF.∴
BD=CF.
∵BD平分∠ABC,
∴∠CBE=∠FBE.
又BE=BE,∴△BCE≌△BFE.
∴CE=EF.
∴BD=2CE.
练习
1.如图.在△ABC中.BE是角平分线.AD丄BE.垂足为D.求证:∠2=∠1+∠C.
证明:延长AD交BC于F,∵AD⊥BE,
∴∠ADB=∠BDF=90°,
∵∠ABD=∠FBD,
∴
∠2=∠BFD.
∵∠BFD=∠1+∠C,∴∠2=∠1+∠C.
2.如图.在△ABC中.
∠ABC=3∠C,AD是∠BAC的平分线,
BE丄AD于点E.
求证:.
(2)证明:延长BE交AC于点F.∵AD为∠BAC的角平分线,∴∠BAD=∠CAD.∵AE=AE,
∴∠BAE=∠FAE,则△AEB≌△AEF,∴AB=AF,
BE=EF,
∠
2=∠3.∴AC-AB=AC-AF=FC.
∵∠ABC=3∠C,∴∠2+∠1=∠3+∠1=∠1+∠C+∠1=3∠C.∴2∠1=2∠C
即∠1=∠C
∴BF=FO=2BE.∴
模型4
角平分线+平行线
模型分析
有角平分线时.常过角平分线上一点作角的一边的平行线.
构造等腰三角形.为证明结论提供更多的条件.体现了用平分线与等腰三角形之间的密切关系.
模型实例
解答下列问题:
(1)如图①.△ABC中,EF∥BC,点D在EF上,BD、CD分别平分∠ABC、∠ACB.写出线段EF与BE、CF有什么数量关系?
(2)如图②,BD平分∠ABC,CD平分外角∠ACG.
DE//BC交AB于点E,交AC于点F,线段EF与BE、CF有什么数量关系?并说明理由.
(3)如图③,BD、CD为外角∠CBM、∠BCN的平分线,DE//BC交AB延长线于点E.交AC延长线于点F,直接写出线段EF与BE、CF有什么数关系?
解答:(1)
∵EF//BC,∴∠EDB=∠DBC.∴BD平分∠EBC,∴∠EBD=∠DBC=EDB.
∴EB=ED.
同理:DF=FC.
∴EF=ED+DF=BE+CF.
(2)图②中有EF=BE=CF,BD平分∠BAC,∴∠ABD=∠DBC.又DE//BC、∴∠EDB=∠DBC.
∴DE=EB.同理可证:CF=DF
∴EF=DE-DF=BE-CF.
(3)
EF=BE+CF.
练习
1.如图.
在△ABC中,∠ABC和∠ACB的平分线交于点E.过点E作MN∥BC交AB于M点.
交AC于N点.若BM+CN=9,则线段MN的长为
.
解答:∵∠ABC、∠ACB的平分线相交于点E,∴MBE=∠EBC,∠ECN=∠ECB.∵MN//BC,
∴∠EBC=∠MEB,
∠NEC=∠ECB.
∴∠MBE-∠MEB,
∠NEO=∠ECN.∴BM=ME,
EN=CN.
∴MN=ME+EN,即MN=BM+CN.∵BM+CN=9,∴MN=9.
2.
如图.
在△ABC中,AD平分∠BAC.点E、F分別在BD,AD上,EF∥AB.且DE=CD,求证:EF=AC.
证明:如图,过点C作CM∥AB交AD的延长线于点M,∵AB∥EF,∴CM∥EF.∴∠3=∠4.
∵DE=CD,
∠5=∠6,
∴△DEF≌△DCM.∴EF=CM.
∵AB//CM,∴∠2=∠4.
∵∠1=∠2,
∴∠1=∠4.∴CM=AC.∴EF=AC
3.如图.梯形ABCD中,AD∥BC,点E在CD上,且AE平分∠BAD.BE平分∠ABC.求证:AD=AB-BC.
证明:延长AD、BE交于点F.∵AD∥BC,∴∠2=∠F.
∵∠1=∠2,∴∠1=∠F.∴AB=AF.
∵AE平分∠BAD∴BE=EF.
∵∠DEF=∠CEB,
∴△DEF≌△CEB.∴DF=BC.∴AD=AF-DF=AB-BC.
截长补短辅助线模型
模型:截长补短
如图①,若证明线段AB、CD、EF之间存在EF=AB+CD,可以考虑截长补短法.
截长法:如图②,在EF上截取EG=AB,再证明GF=CD即可.
补短法:如图③,延长AB至H点,使BH=CD,再证明AH=EF即可.
模型分析
截长补短的方法适用于求证线段的和差倍分关系.
截长,指在长线端中截取一段等于已知的线段;补短,指将一条短线端延长,延长部分等于已知线段.
该类题目中常出现等腰三角形、角平分线等关键词句,可以采用截长补短法构造全等三角形来完成证明过程.
模型实例
例1:如图,已知在△ABC中,∠C=2∠B,∠1=∠2
.
求证:AB=AC+CD
.
证法一,截长法:
如图①,在AB上取一点E,使AE=AC,连接DE.
∵AE=AC,∠1=∠2,AD=AD,
∴△ACD≌△AED
,
∴CD=DE,∠C=∠3
.
∵∠C=2∠B,
∴∠3=2∠B=∠4+∠B
,
∴∠4=∠B
,
∴DE=BE
,
∴CD=BE.
∵AB=AE+BE,
∴AB=AC+CD
.
证法二,补短法:
如图②,延长AC到点E,使CE=CD,连接DE
.
∵CE=CD,∴∠4=∠E
.
∵∠3=∠4+∠E,∴∠3=2∠E
.
∵∠3=2∠B,∴∠E=∠B
.
∵∠1=∠2,AD=AD,
∴△EAD≌△BAD,∴AE=AB.
又∵AE=AC+CE,
∴∴AB=AC+CD
.
例2:如图,已知OD平分∠AOB,DC⊥OA于点C,∠A=∠GBD
.
求证:AO+BO=2CO
.
证明:在线段AO上取一点E,使CE=AC,连接DE
.
∵CD=CD,DC⊥OA,
∴△ACD≌△ECD,
∴∠A=∠CED
.
∵∠A=∠GBD
,
∴∠CED=∠GBD
,
∴1800-∠CED=1800-∠GBD
,
∴∠OED=∠OBD
.
∵OD平分∠AOB,
∴∠AOD=∠BOD
.
∵OD=OD,
∴△OED≌△OBD
,
∴OB=OE,
∴AO+BO=AO+OE=OE+2CE+OE=OE+CE+OE+CE=2(CE+OE)=2CO
.
跟踪练习
1.
如图,在△ABC中,∠BAC=600,AD是∠BAC的平分线,且AC=AB+BD
.
求∠ABC的度数
.
【答案】
证法一:补短
延长AB到点E,使BE=BD
.
在△BDE中,
∵BE=BD,∴∠E=∠BDE,
∴∠ABC=∠BDE+∠E=2∠E
.
又∵AC=AB+BD,
∴AC=AB+BE,∴AC=AE
.
∵AD是∠BAC的平分线,∠BAC=600,
∴∠EAD=∠CAD=600÷2=300
.
∵AD=AD,
∴△AED≌△ACD,∴∠E=∠C
.
∵∠ABC=2∠E,∴∠ABC=2∠C
.
∵∠BAC=600,
∴∠ABC+∠C=1800-600=1200,
∴∠ABC=1200,∴∠ABC=800
.
证法二:在AC上取一点F,使AF=AB,连接DF.
∵AD是∠BAC的平分线,
∴∠BAD=∠FAD
.
∵AD=AD,
∴△BAD≌△FAD,
∴∠B=∠AFD,BD=FD
.
∵AC=AB+BD,AC=AF+FC
∴FD=FC
,∴∠FDC=∠C
.
∵∠AFD=∠FDC+∠C,
∴∠B=∠FDC+∠C=2∠C
.
∵∠BAC+∠B+∠C=1800,
∴∠ABC=1200,∴∠ABC=800
.
2.
如图,在△ABC中,∠ABC=600,AD、CE分别平分∠BAC、∠ACB
.
求证:AC=AE+CD
.
【答案】如图,在AC边上取点F,使AE=AF,连接OF
.
∵∠ABC=600,∴∠BAC+∠ACB=1800-∠ABC=1200
.
∵AD、CE分别平分∠BAC、∠ACB,
∴∠OAC=∠OAB=,∠OCA=∠OCB=,
∴∠AOE=∠COD=∠OAC+∠OCA==600,
∴∠AOC=1800-∠AOE=1200
.
∵AE=AF,∠EAO=∠FAO,AO=AO,
∴△AOE≌△AOF(SAS),
∴∠AOF=∠AOE=600,
∴∠COF=∠AOC-∠AOF=600,
∴∠COF=∠COD
.
∵CO=CO,CE平分∠ACB,
∴△COD≌△COF(ASA),
∴CD=CF
.
∵AC=AF+CF,
∴AC=AE+CD,
3.
如图,∠ABC+∠BCD=1800,BE、CE分别平分∠ABC、∠DCB
.求证:AB+CD=BC
.
【答案】证法一:截长
如图①,在BC上取一点F,使BF=AB,连接EF
.
∵∠1=∠ABE,BE=BE,
∴△ABE≌△FBE,∴∠3=∠4
.
∵∠ABC+∠BCD=1800,
BE、CE分别平分∠ABC、∠DCB,
∴∠1+∠2=∠ABC+∠DCB
=×1800=900
,
∴∠BEC=900
,
∴∠4+∠5=900,∠3+∠6=900
.
∵∠3=∠4
,∴∠5=∠6
.
∵CE=CE,
∠2=∠DCE
,
∴△CEF≌△CED,∴CF=CD
.
∵BC=BF+CF,AB=BF,∴AB+CD=BC
证法二:补短
如图②,延长BA到点F,使BF=BC,连接EF
.
∵∠1=∠ABE,BE=BE,
∴△BEF≌△BEC,
∴EF=EC,∠BEC=∠BEF
.
∵∠ABC+∠BCD=1800,
BE、CE分别平分∠ABC、∠DCB,
∴∠1+∠2=∠ABC+∠DCB
=×1800=900
,
∴∠BEC=900
,
∴∠BEF=∠BEC=900,
∴∠BEF+∠BEC=1800,
∴C、E、F三点共线
.
∵AB∥CD,∴∠F=∠FCD
.
∵EF=EC,∠FEA=∠DEC,
∴△AEF≌△DEC,
∴AF=CD
.
∵BF=AB+AF,
∴BC=AB+CD
.
4.
如图,在△ABC中,∠ABC=900,AD平分∠BAC交BC于D,∠C=300,BE⊥AD于点E
.
求证:AC-AB=2BE
.
【答案】延长BE交AC于点M
.
∵BE⊥AD,∴∠AEB=∠AEM=900
.
∵∠3=900-∠1,∠4=900-∠2,∠1=∠2,
∴∠3=∠4,∴AB=AM
.
∵BE⊥AE,∴BM=2BE
.
∵∠ABC=900,∠C=300,
∴∠BAC=600
.
∵AB=AM,∴∠3=∠4=600,
∴∠5=900-∠3=300,
∴∠5=∠C,∴CM=BM,
∴AC-AB=CM=BM=2BE
.
5.
如图,Rt△ACB中,A=BC,AD平分∠BAC交BC于点D,CE⊥AD交AD于点F,交AB于点E
.
求证:AD=2DF+CE
.
【答案】在AD上取一点G,使AG=CE,连接CG
.
∵CE⊥AD,
∴∠AFC=900,∠1+∠ACF=900
.
∵∠2+∠ACF=900,∴∠1=∠2
.
∵AC=BC,AG=CE,
∴△ACG≌△CBE,∴∠3=∠B=450,
∴∠2+∠4=900-∠3=450
.
∵∠2=∠1=∠BAC=22.50,
∴∠4=450-∠2=22.50,
∴∠4=∠2=22.50
.
又∵CF=CF,DG⊥CF,
∴△CDF≌△CGF,∴DF=GF
.
∵AD=AG+DG,∴AD=CE+2DF
.
6.
如图,五边形ABCDE中,AB=AE,BC+DE=CD,∠B+∠E=1800
.
求证:AD平分∠CDE
.
【答案】如图,延长CB到点F,使BF=DE,连接AF、AC
.
∵∠1+∠2=1800,∠E+∠1=1800,∴∠2=∠E
.
∵AB=AE,∠2=∠E,BF=DE,
∴△ABF≌△AED,∴∠F=∠4,AF=AD
.
∵BC+DE=CD,∴BC+BF=CD,即FC=CD
.
又∵AC=AC,∴△ACF≌△ACD,
∴∠F=∠3
.
∵∠F=∠4,
∴∠3=∠4,
∴AD平分∠CDE
.
手拉手模型
模型 手拉手
如图,△ABC是等腰三角形、△ADE是等腰三角形,AB=AC,AD=AE,∠BAC=∠DAE=.
结论:连接BD、CE,则有△BAD≌△CAE.
模型分析
如图①,
∠BAD=∠BAC-∠DAC,∠CAE=∠DAE-∠DAC.
∵∠BAC=∠DAE=,
∴∠BAD=∠CAE.
在△BAD和△CAE中,
图②、图③同理可证.
(1)这个图形是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.
(2)如果把小等腰三角形的腰长看作小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,所以把这个模型称为手拉手模型.
(3)手拉手模型常和旋转结合,在考试中作为几何综合题目出现.
模型实例
例1 如图,△ADC与△EDG都为等腰直角三角形,连接AG、CE,相交于点H,问:
(1)AG与CE是否相等?
(2)AG与CE之间的夹角为多少度?
解答:
(1)AG=CE.理由如下:
∵∠ADG=∠ADC+∠CDG,∠CDE=∠GDE+∠CDG,∠ADC=∠EDG=90°,
∴∠ADG=∠CDE.
在△ADG和△CDE中,
∴△ADE≌△CDE.
∴AG=CE.
(2)∵△ADG≌△CDE,
∴∠DAG=∠DCE.
∵∠COH=∠AOD,
∴∠CHA=∠ADC=90°.
∴AG与CE之间的夹角是90°.
例2 如图,在直线AB的同一侧作△ABD和△BCE,△ABD和△BCE都是等边三角形,连接AE、CD,二者交点为H.
求证:(1)△ABE≌△DBC;
(2)AE=DQ;
(3)∠DHA=60°;
(4)△AGB≌△DFB;
(5)△EGB≌△CFB;
(6)连接GF,GF∥AC;
(7)连接HB,HB平分∠AHC.
证明:(1)∠ABE=120°,∠CBD=120°,
在△ABE和△DBC中,
∴△ABE≌△DBC.
(2)∵△ABE≌△DBC,
∴AE=DC.
(3)△ABE≌△DBC,
∴∠1=∠2.
∴∠DGH=∠AGB.
∴∠DHA=∠4=60°.
(4)∵∠5=180°-∠4-∠CBE=60°,
∴∠4=∠5.
∵△ABE≌△DBC,
∴∠1=∠2.
又∵AB=DB,
∴△AGB≌△DFB(ASA).
(5)同(4)可证△EGB≌△CFB(ASA).
(6)如图①所示,连接GF.
由(4)得,△AGB≌△DFB.
∴BG=BF.
又∵∠5=60°,
∴△BGF是等边三角形.
∴∠3=60°.
∴∠3=∠4.
∴GF∥AC.
(7)如图②所示,过点B作BM⊥DC于M,过点B作BN⊥AE于点N.
∵△ABE≌△DBC,
∴S△ABE=S△DBC.
∴×AE×BN=×CD×BM.
∵AE=CD,
∴BM=BN.
∵点B在∠AHC的平分线上.
∴HB平分∠AHC.
跟踪练习:
1.
在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:BE=BF;
(2)若∠CAE=30°,求∠ACF度数.
答案:
(1)证明:∠ABC=90°.
在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL).
∴BE=BF.
(2)∵AB=CB,∠ABC=90°,
∴∠BAC=∠BCA=45°.
∴∠CAE=30°.
∴∠BAE=45°-30°=15°.
∵Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°.
∴∠ACF=∠BCF+∠BCA=15°+45°=60°.
2.如图,△ABD与△BCE都为等边三角形,连接AE与CD,延长AE交CD于点H.
求证:(1)AE=DC;
(2)∠AHD=60°;
(3)连接HB,HB平分∠AHC.
答案:
(1)∵∠ABE=∠ABD-∠EBD,∠DBC=∠EBC-∠EBD,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC.
在△ABE和△DBC中,
∴△ABE≌△DBC.
∴AE=DC.
(2)∵△ABE≌△DBC
,
∴∠EAB=∠CDB.
又∵∠OAB+∠OBA=∠ODH+∠OHD,
∴∠AHD=∠ABD=60°.
(3)过B作AH、DC的垂线,垂足分别为点M、N.
∵△ABE≌△DBC,
∴S△ABE=S△DBC.
即AE·BM=CD·BN.
又∵AE=CD,
∴BM=BN.
∴HB平分∠AHC.
3.在线段AE同侧作等边△ABC和等边△CDE(∠ACE<120°),点P与点M分别是线段BE和AD的中点.
求证:△CPM是等边三角形.
答案:
证明:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE.
∴∠ACB=∠ECD=60°.
∴∠BCE=∠ACD.
∴△BCE≌△ACD.
∴∠CBE=∠CAD,BE=AD.
又∵点P与点M分别是线段BE和AD的中点,
∴BP=AM.
在△BCP和△ACM中,
∴△BCP≌△ACM.
∴PC=MC,∠BCP=∠ACM.
∴∠PCM=∠ACB=60°.
∴△CPM是等边三角形.
4.
将等腰Rt△ABC和等腰Rt△ADE按图①方式放置,∠A=90°,AD边与AB边重合,AB=2AD=4.将△ADE绕A点逆时针方向旋转一个角度(0°<<180°),BD的延长线交CE于P.
(1)如图②,求明:BD=CE,BD⊥CE;
(2)如图③,在旋转的过程中,当AD⊥BD时,求CP长.
答案:
(1)∵等腰Rt△ABC和等腰Rt△ADE,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°.
∵∠DAB=90°-∠CAD,∠CAE=90°-∠CAD,
∴∠DAB=∠CAE.
∴△ABD≌△ACE.
∴BD=CE.
∴∠DBA=∠ECA.
∴∠CPB=∠CAB.(8字模型)
∴BD⊥CE.
(2)由(1)得BP⊥CE.
又∵AD⊥BD,∠DAE=90°,AD=AE,
∴四边形ADPE为正方形.
∴AD=PE=2.
∴∠ADB=90°,AD=2,AB=4,
∴BD=CE=.
∴CP=CE-PE=.
三垂直全等模型
模型
三垂直全等模型
如图:∠D=∠BCA=∠E=90°,BC=AC.
结论:Rt△BCD≌Rt△CAE.
模型分析
说到三垂直模型,不得不说一下弦图,弦图的运用在初中直角三角形中占有举足轻重的地位,很多利用垂直求角,勾股定理求边长,相似求边长都会用到从弦图支离出来的一部分几何图形去求解.图①和图②就是我们经常会见到的两种弦图.
三垂直图形变形如下图③、图④,这也是由弦图演变而来的.
例1
如图,AB⊥BC,CD⊥BC,AE⊥DE,AE=DE,求证:AB+CD=BC.
证明:∵AE⊥DE,AB⊥BC,DC⊥BC,
∴∠AED=∠B=∠C=90°.
∴∠A+∠AEB=∠AEB+∠CED=90°.
∴∠BAE=∠CED.
在△ABE和△ECD中,
∴△ABE≌△ECD.
∴AB=EC,BE=CD.
∴AB+CD=EC+BE=BC.
例2
如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,BE=0.8cm,则DE的长为多少?
解答:∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°.
∴∠EBC+∠BCE=90°.
∵∠BCE+∠ACD=90°,
∴∠EBC=∠DCA.
在△CEB和△ADC中,
∴△CEB≌△ADC.
∴BE=DC=0.8cm,CE=AD=2.5cm.
∴DE=CE-CD=2.5-0.8=1.7cm.
例3
如图,在平面直角坐标系中,等腰Rt△ABC有两个顶点在坐标轴上,求第三个顶点的坐标.
解答:(1)如图③,过点B作BD⊥x轴于点D.
∴∠BCD+∠DBC=90°.
由等腰Rt△ABC可知,BC=AC,∠ACB=90°,
∴∠BCD+∠ACO=90°.
∴∠DBC=∠ACO.
在△BCD和△CAO中,
∴△BCD≌△CAO.
∴CD=OA,BD=OC.
∵OA=3,OC=2.
∴CD=3,BD=2.
∴OD=5.
∴B(-5,2).
(2)如图④,过点A作AD⊥y轴于点D.
在△ACD和△CBO中,
∴△ACD≌△CBO.
∴CD=OB,AD=CO.
∵B(-1,0),C(0,3)
∴OB=1,OC=3.
∴AD=3,OD=2.
∴OD=5.
∴A(3,2).
跟踪练习
1.如图,正方形ABCD,BE=CF.求证:(1)AE=BF;(2)AE⊥BF.
证明:
(1)∵四边形ABCD是正方形,
∴AB=BD,∠ABC=∠BCD=90°.
在△ABE和△BCF中,
∴△ABE≌△BCF.
∴AE=BF.
(2)∵△ABE≌△BCF.
∴∠BAE=∠CBF.
∵∠ABE=90°,
∴∠BAE+∠AEB=90°.
∴∠CBF+∠AEB=90°.
∴∠BGE=90°,
∴AE⊥BF.
2.直线l上有三个正方形a、b、c,若a、c的面积分别是5和11,则b的面积是_____.
解答:∵a、b、c都是正方形,
∴AC=CD,∠ACD=90°.
∵∠ACB+∠DCE=∠ACB+∠BAC=90°,
∴∠BAC=∠DCE.
在△ABC和△CBE中,
∴△ACB≌△CDE.
∴AB=CE,BC=DE.
在Rt△ABC中,=+=+
即=+=5+11=16.
3.已知,△ABC中,∠BAC=90°,AB=AC,点P为BC上一动点(BP(1)求证:EF=CF-BE;
(2)若P为BC延长线上一点,其它条件不变,则线段BE、CF、EF是否存在某种确定的数量关系?画图并直接写出你的结论.
解答:∵BE⊥AP,CF⊥AP,
∴∠AEB=∠AFC=90°.
∴∠FAC+∠ACF=90°,
∵∠BAC=90°,
∴∠BAE+∠FAC=90°,
∴∠BAE=∠ACF.
在△ABE和△CAF中,
∴△ABE≌△CAF.
∴AE=CF,BE=AF.
∵EF=AE-AF,
∴EF=CF-BE.
(2)如图,EF=BE+CF.
理由:同(1)易证△ABE≌△CAF.
∴AE=CF,BE=AF.
∵EF=AE+AF,
∴EF=
BE
+
CF.
4.如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,设∠BCD=α,以D为旋转中心,将
腰DC绕点D逆时针旋转90°至DE.
(1)当α=45°时,求△EAD的面积;
(2)当α=45°时,求△EAD的面积;
(3)当0°<α<90°,猜想△EAD的面积与α大小有无关系?若有关,写出△EAD的面积S与α的关系式;若无关,请证明结论.
解答:
(1)1;
(2)1;
(3)过点D作DG⊥BC于点G,过点E作EF⊥AD交AD延长线于点F.
∵AD∥BC,DG⊥BC,
∴∠GDF=90°.
又∵∠EDC=90°,
∴∠1=∠2.
在△CGD和△EFD中,
∴△DCG≌△DEF
∴EF=CG,
∵AD∥BC,AB⊥BC,AD=2,BC=3,
∴BG=AD=2,
∴CG=1.
∴=AD·EF=1.
∴△EAD的面积与α大小无关.
5.向△ABC的外侧作正方形ABDE、正方形ACFG,过A作AH⊥BC于H,AH的反向延长线与EG交于点P.
求证:BC=2AP.
解答:过点G作GM⊥AP于点M,过点E作EN⊥AP交AP延长线于点N.
∵四边形ACFG是正方形,
∴AC=AG,∠CAG=90°.
∴∠CAH+∠GAM=90°.
又∵AH⊥BC,
∴∠CAH+∠ACH=90°.
∴∠ACH=∠GAM.
在△ACH和△GAM中,
∴△ACH≌△GAM
∴CH=AM,AH=GM.
同理可证△ABH≌△EAN
∴BH=AN,AH=EN.
∴EN=GM.
在△EPN和△GPM中,
∴△EPN≌△GPM.
∴NP=MP,
∴BC=BH+CH
=AN+AM
=AP+PN+AP-PM
=2AP.
中考复习专题(将军饮马问题题型归纳)
一、求线段和最值
(一)两定一动型
例1:如图,AM⊥EF,BN⊥EF,垂足为M、N,
MN=12m,AM=5m,BN=4m,P是EF上任意一点,则PA+PB的最小值是________
m
分析:这是最基本的将军饮马问题,A、B是定点,P是动点,属于两定一动将军饮马型,根据常见的“定点定线作对称”,可作点A关于EF的对称点A/,根据两点之间,线段最短,连接A/B,此时A/P+PB即为A/B,最短.而要求A/B,则需要构造直角三角形,利用勾股定理解决
解答:
作点A关于EF的对称点A/,过点A作A/C⊥BN的延长线于C.易知A/M=AM=NC=5m,BC=9m,A/C=MN=12m,在Rt△A/BC中,A/B=15m,即PA+PB的最小值是15m
变式:如图,在边长为2的正三角形ABC中,E,F,G为各边中点,P为线段EF上一动点,则△BPG周长的最小值为_________
分析:考虑到BG为定值是1,则△BPG的周长最小转化为求BP+PG的最小值,又是两定一动的将军饮马型,考虑作点G关于EF的对称点,这里有些同学可能看不出来到底是哪个点,我们不妨连接AG,则AG⊥BC,再连接EG,根据“直角三角形斜边中线等于斜边的一半”,可得AE=EG,则点A就是点G关于EF的对称点.最后计算周长时,别忘了加上BG的长度
解答:
连接AG,易知PG=PA,BP+PG=BP+PA,当B,P,A三点共线时,BP+PG=BA,此时最短,BA=2,BG=1,即△BPG周长最短为3
(二)、一定两动型
例2:如图,在△ABC中,AB=AC=5,D为BC中点,AD=5,P为AD上任意一点,E为AC上任意一点,求PC+PE的最小值.
分析:这里的点C是定点,P、E是动点,属于一定两动的将军饮马模型,由于△ABC是等腰三角形,AD是BC中线,则AD垂直平分BC,点C关于AD的对称点是点B,PC+PE=PB+PE,显然当B、P、E三点共线时,BE更短。但此时还不是最短,根据“垂线段最短”只有当BE⊥AC时,BE最短,求BE时,用面积法即可.
解答:
作BE⊥AC交于点E,交AD于点P,易知AD⊥BC,BD=3,BC=6,
则AD·BC=BE·AC,
4×6=BE·5,
BE=4.8
变式:如图,BD平分∠ABC,E,F分别为线段BC,BD上的动点,AB=8,△ABC的周长为20,求EF+CF的最小值__________
分析:
这里的点C是定点,F,E是动点,属于一定两动的将军饮马模型,我们习惯于“定点定线作对称”,但这题这样做,会出现问题.因为点C的对称点C/必然在AB上,但由于BC长度未知,BC/长度也未知,则C/相对的也是不确定点,因此我们这里可以尝试作动点E关于BD的对称点.
解答:
如图,作点E关于BD的对称点E/,连接E/F,则EF=E/F+CF,当E/
、F、C三点共线时,E'F+CF=E'C,此时较短.过点C作CE"⊥AB于E",当,E'与E"重合时,E"C最短,E"C为AB边上的高,E"C=5.
(三)、两点两动型
例3:如图,∠AOB=30°,0C=5,OD=12,点E,F分别是射线OA,OB上的动点,求CF+EF+DE的最小值.
分析:这里的点C,点D是定点,F,E是动点,属于两定两动的将军饮马模型,依旧可以用“定点定线作对称来考虑.作点C关于OB的对称点,点D关于OA的对称点.
解答:作点C关于OB的对称点C′,点D关于0A的对称点D′,连接C′D′.CF+EF+DE=C′F+EF+D′E,当C′,F,E,D′四点共线时,CF+EF+DE=C′D′最短.易知∠D'OC′=90°,OD′=12,OC′=5,C′D'=13,CF+EF+DE最小值为13.
变式:如图,斯诺克比赛桌面AB宽1.78m,白球E距AD边0.22m,距CD边1.4m,有一颗红球F紧贴BC边,且距离CD边0.1m,若要使白球E经过边AD,DC,两次反弹击中红球F,求白球E运动路线的总长度.
分析:本题中,点E和点F是定点,两次反弹的点虽然未知,但我们可以根据前几题的经验作出,即分别作点E关于AD边的对称点E',作点F关于CD边的对称点F',即可画出白球E的运动路线,化归为两定两动将军饮马型.
解答:作点E关于AD边的对称点E′,作点F关于CD边的对称点F′,连接E′F',交AD于点G,交CD于点H,则运动路线长为EG+GH+HF长度之和,即E′F′长,延长E′E交BC于N,交AD于M,易知E′M=EM=0.22m,E′N=1.78+0.22=2m,NF′=NC+CF'=1.4+0.1=1.5m,
则Rt△E′NF′中,E′F′=2.5m,即白球运动路线的总长度为2.5m.
小结:以上求线段和最值问题,几乎都可以归结为“两定一动”、”一定两动”、“两定两动”类的将军饮马型问题,基本方法还是“定点定线作对称”,利用“两点之间线段最短“垂线段最短"的2条重要性质,将线段和转化为直角三角形的斜边,或者一边上的高,借助勾股定理,或者面积法来求解.
当然,有时候,我们也需学会灵活变通,定点对称行不通时,尝试作动点对称.
(二)求角度
例4:P为∠AOB内一定点,M、N分别为射线OA、OB上一
点,当△PMN周长最小时,∠
MPN=80°.
(1)∠AOB=_________°
(2)求证:OP平分∠
MPN
分析:这又是一定两动型将军饮马问题,我们应该先将M,N的位置找到,再来思考∠AOB的度数,显然作点P关于OA的对称点P′,关于OB的对称点P”,连接P′P",其与OA交点即为M,
与OB交点即为N,如下图,易知∠DPC与∠AOB互补,则求出∠DPC的度数即可解答:(1)法1:如图,∠1+∠2=100°,∠1=∠MP′P+∠3=2∠3,∠2=∠NP"P+∠4=2∠4,
则∠3+∠4=50°,∠DPC=130°,∠AOB=50°
再分析:考虑到第二小问要证明OP平分∠MPN,我们就连接OP,则要证∠5=∠6,显然很困难,这时候,考虑到对称性,我们再连接OP',OP",则∠5=∠7,∠6=∠8,问题迎刃而解.
解答:(1)法2易知OP′=0P",∠7+∠8=∠5+∠6=80°,∠P′OP”=100°,由对称性知,∠9=∠11,∠10=∠12,∠AOB=∠9+∠10=50°
(2)由OP′=OP",∠P′OP"=100°知,∠7=∠8=40°∠5=∠6=40°,OP平分∠MPN
变式:如图,在五边形
ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC、DE上分别找一点M、N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为_______
分析:这又是典型的一定两动型将军饮马问题,必然是作A点关于BC、DE的对称点A/、A",连接A/A",与BC、DE的交点即为△AMN周长最小时M、N的位置.
解答:如图
∵∠BAE=136°,
∴∠MA/A+∠NA"A=44°
由对称性知,
∠MAA/=∠MA/A,
∠NAA"=∠NA"A
∠AMN+∠ANM=2∠MA/A+2∠NA"A=88°
本讲思考题:
1.如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为_____
2.如图,在矩形ABCD中
AB=4,AD=3.P为矩形ABCD内一点,若矩形ABCD
面积为△PAB面积的4倍,则点P到A,B两点距离之和PA+PB的最小值为________
蚂蚁行程
模型
立体图形展开的最短路径
模型分析
上图为无底的圆柱体侧面展开图,如图蚂蚁从点A沿圆柱表面爬行一周。到点B的最短路径就是展开图中AB′的长,。做此类题日的关键就是,正确展开立体图形,利用“两点之间线段最短”或“两边之和大于第三边”准确找出最短路径。
模型实例
例1.有一圆柱体油罐,已知油罐底面周长是12m,高AB是5m,要从点A处开始绕油罐一周建造房子,正好到达A点的正上方B处,问梯子最短有
多长?
例2.如图,一直圆锥的母线长为QA=8,底面圆的半径,
若一只小蚂蚁从A点出发,绕圆锥的侧面爬行一周后又回到A点,则蚂蚁爬行的最短
路线长是
。
例3.已知长方体的长、宽、高分别为30cm、20cm、10cm,一只蚂蚁从A处出发到B处觅食,求它所走的最短路径。(结果保留根号)
跟踪练习
1.有一个圆锥体如图,高4cm,底面半径5cm,A处有一蚂蚁,若蚂蚁欲沿侧面爬行到C处,求蚂蚁爬行的最短距离。
2.如图,圆锥体的高为8cm,底面周长为4cm,小蚂蚁在圆柱表面爬行,从A点到B点,路线如图,则最短路程为
。
3.桌上有一个圆柱形无盖玻璃杯,高为12厘米,底面周长18厘米,在杯口内壁离杯口距离3厘米的A处有一滴蜜糖,一只小虫22
杯子外壁,当它正好在蜜糖相对方向离桌面3厘米的B处时,突然发现了蜜糖,问小虫至少爬多少厘米才能到达蜜糖所在的位置。
4.已知O为圆锥顶点,OA、OB为圆锥的母线,C为OB的中点,一只小蚂蚁从点C开始沿圆锥侧面爬行到点A,另一只小蚂蚁也从C点出发绕着圆锥侧面爬行到点B,它们所爬行的最短路线的痕迹如图所示,若沿OA剪开,则得到的圆锥侧面展开图为
(
)
A
B
C
D
5.如图,一只蚂蚁沿着边长为2的正方体表面从点A出发,经过3个面爬行到点B,如果它运动的路径是最短的,则最短距离为
。
6.如图是一个边长为6的正方体木箱,点Q
在上底面的棱上,AQ=2,一只
蚂蚁从P点出发沿木箱表面爬行到点Q,求蚂蚁爬行的最短路线。
7.如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm、3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点的最短路程是多少?
中点四大模型
模型1
倍长中线或类中线(与中点有关的线段)构造全等三角形
模型分析
如图①,AD是△ABC的中线,延长AD至点E使DE=AD,易证:△ADC≌△EDB(SAS).
如图②,D是BC中点,延长FD至点E使DE=FD,易证:△FDB≌△EDC(SAS)
当遇见中线或者中点的时候,可以尝试倍长中线或类中线,构造全等三角形,目的是对已知条件中的线段进行转移.
模型实例
如图,已知在△ABC中,AD是BC边上的中线,E是AD上一点,连接BE并延长交AC于点F,AF=EF,求证:AC=BE.
1.如图,在△ABC中,AB=12,AC=20,求BC边上中线AD的范围.
解:延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC与△EDB中,
,
∴△ADC≌△EDB(SAS),
∴EB=AC=20,
根据三角形的三边关系定理:20-12<AE<20+12,
∴4<AD<16,
故AD的取值范围为4<AD<16.
2.如图,在△ABC中,D是BC的中点,DM⊥DN,如果BM2+CN2=DM2+DN2.
求证:AD2=(AB2+AC2).
证明:如图,过点B作AC的平行线交ND的延长线于E,连ME.
∵BD=DC,
∴ED=DN.
在△BED与△CND中,
∵
∴△BED≌△CND(SAS).
∴BE=NC.
∵∠MDN=90°,
∴MD为EN的中垂线.
∴EM=MN.
∴BM2+BE2=BM2+NC2=MD2+DN2=MN2=EM2,
∴△BEM为直角三角形,∠MBE=90°.
∴∠ABC+∠ACB=∠ABC+∠EBC=90°.
∴∠BAC=90°.
∴AD2=(BC)2=(AB2+AC2).
模型2
已知等腰三角形底边中点,可以考虑与顶点连接用“三线合一”.
模型分析
等腰三角形中有底边中点时,常作底边的中线,利用等腰三角形“三线合一”的性质得到角相等,为解题创造更多的条件,当看见等腰三角形的时候,就应想到:
“边等、角等、三线合一”.
模型实例
如图,在△ABC中,AB=AC=5,BC=6,M为BC的中点,MN⊥AC于点N,求MN的长度.
解答:
连接AM.
∵AB=AC=5,BC=6,点M为BC中点,
∴AM⊥BC,BM=CM=BC=3.
∵AB=5,
∴AM=.
∵MN⊥AC,
∴S△ANC=MC·AM=AC·MN.
即:×3×4=×5×MN.
∴MN=
跟踪练习
1.如图,在△ABC中,AB=AC,D是BC的中点,AE⊥DE,AF⊥DF,且AE=AF,求证:∠EDB=∠FDC.
证明:连结AD,
∵AB=AC,D是BC的中点,
∴AD⊥BC,∠ADB=∠ADC=90°
在Rt△AED与Rt△AFD中,
,
∴Rt△AED≌Rt△AFD.(HL)
∴∠ADE=∠ADF,
∵∠ADB+∠ADC=90°,
∴∠EDB=∠FDC.
2.已知Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC、CB(或它们的延长线)于E、F.
(1)当∠EDF绕D点旋转到DF⊥AC于E时(如图①),求证:S△DEF+S△CEF=S△ABC;
(2)当∠EDF绕D点旋转到DE和AC不垂直时,在图②和图③这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,
S△DEF、S△CEF、S△ABC又有怎样的数量关系?请写出你的猜想,不需要证明.
解:(1)连接CD;如图2所示:
∵AC=BC,∠ACB=90°,D为AB中点,
∴∠B=45°,∠DCE=∠ACB=45°,CD⊥AB,CD=AB=BD,
∴∠DCE=∠B,∠CDB=90°,
∵∠EDF=90°,
∴∠1=∠2,
在△CDE和△BDF中,
,
∴△CDE≌△BDF(ASA),
∴S△DEF+S△CEF=S△ADE+S△BDF=S△ABC;
(2)不成立;S△DEF?S△CEF=S△ABC;理由如下:连接CD,如图3所示:
同(1)得:△DEC≌△DBF,∠DCE=∠DBF=135°
∴S△DEF=S五边形DBFEC,
=S△CFE+S△DBC,
=S△CFE+S△ABC,
∴S△DEF-S△CFE=S△ABC.
∴S△DEF、S△CEF、S△ABC的关系是:S△DEF-S△CEF=S△ABC.
模型3
已知三角形一边的中点,可考虑中位线定理
模型分析
在三角形中,如果有中点,可构造三角形的中位线,利用三角形中位线的性质定理:
DE∥BC,且DE=BC来解题.中位线定理中既有线段之间的位置关系又有数量关系,该模型可以解决角问题,线段之间的倍半、相等及平行问题.
模型实例
如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M,N.求证:∠BME=∠CNE.
解答
如图,连接BD,取BD的中点H,连接HE、HF.
∵E、F分别是BC、AD的中点,
∴FH=AB,FH∥AB,HE=DC,HE∥NC.
又∵AB=CD,
∴HE=HF.
∴∠HFE=∠HEF.
∵FH∥MB,HE∥NC,
∴∠BME=∠HFE,∠CNE=∠FEH.
∴∠BME=∠CNE.
练习:
1.(1)如图1,BD,CE分别是△ABC的外角平分线,过点A作AD⊥BD,AE⊥CE,垂足分别为D,E,连接DE,求证:DE∥BC,DE=(AB+BC+AC);
(2)如图2,BD,CE分别是△ABC的内角平分线,其他条件不变,上述结论是否成立?
(3)如图3,BD是△ABC的内角平分线,CE是△ABC的外角平分线,其他条件不变,DE与BC还平行吗?它与△ABC三边又有怎样的数量关系?请写出你的猜想,并对其中一种情况进行证明.
1.解答
(1)如图①,分别延长AE,AD交BC于H,K.
在△BAD和△BKD中,
∴△BAD≌
△BKD(ASA)
∴AD=KD,AB=KB.
同理可证,AE=HE,AC=HC.
∴DE=HK.
又∵HK=BK+BC+CH=AB+BC+AC.
∴DE=(AB+AC+BC).
(2)猜想结果:图②结论为DE=(AB+AC-BC)
证明:分别延长AE,AD交BC于H,K.
在△BAD和△BKD中
∴△BAD≌△BKD(ASA)
∴AD=KD,AB=KB
同理可证,AE=HE,AC=HC.
∴DE=HK.
又∵HK=BK+CH-BC
=AB+AC-BC
∴DE=(AB+AC-BC)
(3)图③的结论为DE=(BC+AC-AB)
证明:分别延长AE,AD交BC或延长线于H,K.
在△BAD和△BKD中,
∴△BAD
≌△BKD(ASA)
∴AD=KD,AB=KB.
同理可证,AE=HE,AC=HC.
∴DE=KH.
又∵HK=BH-BK
=BC+CH-BK
=BC+AC-AB
∴DE=(BC+AC-AB).
2.问题一:如图①,在四边形ABCD中,AB与CD相交于点O,AB=CD,E,F分别是BC,AD的中点,连接EF,分别交DC,AB于点M,N,判断△OMN的形状,请直接写出结论.
问题二:如图②,在△ABC中,AC>AB,D点在AC上,AB=CD,E,F分别是BC,AD的中点,连接EF并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD的形状并证明.
2.证明
(1)等腰三角形(提示:取AC中点H,连接FH,EH,如图①)
(2)△AGD是直角三角形
如图②,连接BD,取BD的中点H,连接HF,HE.
∵F是AD的中点,
∴HF∥AB,HF=AB.
∴∠1=∠3.
同理,HE∥CD,HE=CD,
∴∠2=∠EFC,
∴AB=CD,
∴HF=HE.
∴∠1=∠2.
∵∠EFC=60°,
∴∠3=∠EFC=∠AFG=60°.
∴△AGF是等边三角形.
∴AF=FG.
∴GF=FD.
∴∠FGD=∠FDG=30°.
∴∠AGD=90°,即△AGD是直角三角形.
模型4
已知直角三角形斜边中点,可以考虑构造斜边中线
模型分析
在直角三角形中,当遇见斜边中点时,经常会作斜边上的中线,利用直角三角形斜边上的中线等于斜边的一半,即CD=AB,来证明线段间的数量关系,而且可以得到两个等腰三角形:△ACD和△BCD,该模型经常会与中位线定理一起综合应用.
模型实例
如图,在△ABC中,BE,CF分别为AC,AB上的高,D为BC的中点,DM⊥
EF于点M,求证:FM=EM.
证明
连接DE,DF.
BE,CF分别为边AC,AB上的高,D为BC的中点,
DF=BC,DE=BC.
DF=DE,即△DEF是等腰三角形.
DM⊥EF,
点M是EF的中点,即FM=EM.
练习:
1.如图,在△ABC中,∠B=2∠C,AD⊥BC于D,M为BC的中点,AB=10,求DM的长度.
1.解答
取AB中点N,连接DN,MN.
在Rt△ADB中,N是斜边AB上的中点,
∴DN=AB=BN=5.
∴∠NDB=∠B.
在△ABC中,M,N分别是BC,AB的中点,
∴MN∥AC
∴∠NMB=∠C,
又∵∠NDB是△NDM的外角,
∴∠NDB=∠NMD+∠DNM.
即∠B=∠NMD+∠DNM=∠C+∠DNM.
又∵∠B=2∠C,
∴∠DNM=∠C=∠NMD.
∴DM=DN.
∴DM=5.
2.已知,△ABD和△ACE都是直角三角形,且∠ABD=∠ACE=90°,连接DE,M为DE的中点,连接MB,MC,求证:MB=MC.
2.证明
延长BM交CE于G,
∵△ABD和△ACE都是直角三角形,
∴CE∥BD.
∴∠BDM=∠GEM.
又∵M是DE中点,即DM=EM,
且∠BMD=∠GME,
∴△BMD
≌△GME.
∴BM=MG.
∴M是BG的中点,
∴在Rt△CBG中,BM=CM.
3.问题1:如图①,三角形ABC中,点D是AB边的中点,AE⊥
BC,BF
⊥AC,垂足分别为点E,F.AE、BF交于点M,连接DE,DF,若DE=kDF,则k的值为
.
问题2:如图②,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC内部,且∠MAC=∠MBC,过点M分别作ME
⊥BC,MF⊥
AC,垂足分别为点E,F,连接DE,DF,求证:DE=DF.
问题3:如图③,若将上面问题2中的条件“CB=CA”变为“CB
≠CA”,其他
条件不变,试探究DE与DF之间的数量关系,并证明你的结论.
3.解答
∵(1)AE⊥BC,BF⊥AC,
∴△AEB和△AFB都是直角三角形,
∵D是AB的中点,
∴DE=AB,DF=AB.
∴DE=DF.
∵DE=KDF,
∴k=1.
(2)∵CB=CA,
∴∠CBA=∠CAB.
∵∠MAC=∠MBC,
∴∠CBA-∠MBC=∠CAB-∠MAC,即∠ABM=∠BAM.
∴AM=BM.
∵ME⊥BC,MF⊥AC,
∴∠MEB=∠MFA=90°.
又∵∠MBE=∠MAF,
∴△MEB
≌△MFA(AAS)
∴BE=AF.
∵D是AB的中点,即BD=AD,
又∵∠DBE=∠DAF,
∴△DBE
≌△DAF(SAS)
∴DE=DF.
(3)DE=DF.
如图,作AM的中点G,BM的中点H,连DG,FG,DH,EH.
∵点D是边AB的中点,
∴DG∥BM,DG=BM.
同理可得:DH∥AM,DH=AM.
∵ME⊥BC于E,H是BM的中点.
∴在Rt△BEM中,HE=BM=BH.
∴∠HBE=∠HEB.
∴∠MHE=2∠HBE.
又∵DG=BM,HE=BM,
∴DG=HE.
同理可得:DH=FG.
∠MGF=2∠MAC.
∵DG∥BM,DH∥GM,
∴四边形DHMG是平行四边形.
∴∠DGM=∠DHM.
∵∠MGF=2∠MAC,
∠MHE=2∠MBC,
∠MBC=∠MAC,
∴∠MGF=∠MHE.
∴∠DGM+∠MGF=∠DHM+∠MHE.
∴∠DGF=∠DHE.
在△DHE与△FGD中
∴△DHE≌
△FGD(SAS)
∴DE=DF.
半角模型
模型概述:
过多边形的某个顶点引两条射线,使这两条射线的夹角为该顶角的一半
思想方式:
通过旋转变换构造全等三角形,实现线段的转化
基本模型:
一、正方形含半角
如图,在正方形ABCD中,E,F分别是BC,CD边上的点,∠EAF=45°,证明以下结论:
⑴EF=BE+DF;
⑵△CEF的周长是正方形边长的2倍;
⑶FA平分∠DFE,EA平分∠BEF;
⑷
【小结】
变式训练1-1
如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45?.
(1)如图(1),试判断EF,BE,DF间的数量关系,并说明理由;
(2)如图(2),若AH⊥EF于点H,试判断线段AH与AB的数量关系,并说明理由。
变式训练1-2
探究:
(1)如图1,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45?,试判断BE、DF与EF三条线段之间的数量关系,直接写出判断结果:___;
(2)如图2,若把(1)问中的条件变为“在四边形ABCD中,AB=AD,∠B+∠D=180?,E、F分别是边BC、CD上的点,且∠EAF=∠BAD”,则(1)问中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;
(3)在(2)问中,若将△AEF绕点A逆时针旋转,当点分别E.?F运动到BC、CD延长线上时,如图3所示,其它条件不变,则(1)问中的结论是否发生变化?若变化,请给出结论并予以证明。
二、等腰直角三角形含半角
如图,等腰Rt△ABC中,∠ACB=90°,AC=BC,过点C作∠DCE=45°,交AB边于D,E两点。
证明:⑴△ACE∽△BDC;
⑵
【小结】
变式训练2-1
如图,等腰Rt△ABC中,∠ACB=90°,AC=BC,过点C作∠DCE=45°,交AB边于D,E两点。
⑴若AD=6,AE=16,则BE=
⑵若AB=12,DE=5,AD<BE,则BE=
⑶若,BD=5,则AE=
变式训练2-2
在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60?,∠BDC=120?,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系。
(1)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是___;此时QL=___;
(2)如图2,点M、N边AB、AC上,且当DM≠DN时,猜想(1)问的两个结论还成立吗?写出你的猜想并加以证明;
(3)如图3,当M、N分别在边AB、CA的延长线上时,若AN=x,则Q=___(用x、L表示).
变式训练2-3
(1)如图1,点E.?F分别是正方形ABCD的边BC、CD上的点,∠EAF=45?,连接EF,
则EF、BE、FD之间的数量关系是:EF=BE+FD.连结BD,交AE、AF于点M、N,且MN、BM、DN满足,请证明这个等量关系;
(2)在△ABC中,AB=AC,点D.?E分别为BC边上的两点。
①如图2,当∠BAC=60?,∠DAE=30?时,BD、DE、EC应满足的等量关系是___;
②如图3,当∠BAC=α,(0?<α<90?),∠DAE=α时,BD、DE、EC应满足的等量关系是___.[参考:】
中考真题
如图,已知△ABC,∠ACB=90?,AC=BC,点E.?F在AB上,∠ECF=45?.
(1)求证:△ACF∽△BEC;
(2)设△ABC的面积为S,求证:AF?BE=2S;
(3)试判断以线段AE、EF、FB为边的三角形的形状并给出证明。
已知:如图,正方形ABCD,BM、DN分别平分正方形的两个外角,且满足∠MAN=45?,连接MN.
(1)若正方形的边长为a,求BM?DN的值。
(2)若以BM,DN,MN为三边围成三角形,试猜想三角形的形状,并证明你的结论。
已知:正方形ABCD中,∠MAN=45?,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.
(1)当∠MAN绕点A旋转到BM≠DN时(图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明。
(2)当∠MAN绕点A旋转到(图3)的位置时,线段BM,DN和MN之间又有怎样的数量关系?证明你的猜想。
(3)若正方形的边长为4,当点N运动到DC边的中点处时,求BM的长。
问题背景:
(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120?,∠B=∠ADC=90?.E,F分别是BC,CD上的点。且∠EAF=60?.探究图中线段BE,EF,FD之间的数量关系。小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是___.
探索延伸:
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180?.E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由。
如图,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30?的A处,舰艇乙在指挥中心南偏东70?的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/时的速度前进,舰艇乙沿北偏东50?的方向以80海里/时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E.?F处,且两舰艇之间的夹角为70?,试求此时两舰艇之间的距离。
问题:如图(1),点E.?F分别在正方形ABCD的边BC、CD上,∠EAF=45?,试判断BE、EF、FD之间的数量关系。
【发现证明】
小聪把△ABE绕点A逆时针旋转90?至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论。
【类比引申】
如图(2),四边形ABCD中,∠BAD≠90?,AB=AD,∠B+∠D=180?,点E.?F分别在边BC、CD上,则当∠EAF与∠BAD满足___关系时,仍有EF=BE+FD.
【探究应用】
如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60?,∠ADC=120?,∠BAD=150?,道路BC、CD上分别有景点E.?F,且AE⊥AD,DF=40()米,现要在E.?F之间修一条笔直道路,求这条道路EF的长
相似模型
模型1:A、8模型
已知∠1=∠2
结论:△ADE∽△ABC
模型分析
如图,在相似三角形的判定中,我们通过做平行线,从而得出A型或8型相似.在做题使,我们也常常关注题目由平行线所产生的相似三角形.
模型实例
【例1】如图,在ABC中,中线AF、BD、CE相交于点O,求证:.
解答:证法一:如图①,连接DE.∵D、E是中点,∴.,DE//BC
∴△EOD∽△COB(8模型)∴.同理:,.
∴.
证法二:如图②,过F作FG//AC交BD于点G,∵F是中点,∴.
∵AD=CD,∴.∵FG//AD,∴△GOF∽△DOA(8模型)
∴.同理,.∴.
【例2】如图,点E、F分别在菱形ABCD的边AB、AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若=2,求的值.
解答:∵四边形ABCD是菱形,∴AB=BC=CD=AD.
设DF=a,则DF=AE=a,AF=EB=2a.∵HD//AB,∴△HFD∽△BFA
∴,∴HD=1.5a,,∴FH=BH
∵HD//EB,∴△DGH∽△EGB,∴,∴
∴BG=HB,∴
跟踪练习:
1.如图,D、E分别是△ABC的边AB、BC上的点,且DE//AC,AE、CD相交于点O,若S△DOE:S△COA=1:25.则S△BDE与S△CDE的比是____________.
解答:∵DE//AC,∴△DOE∽△COA,又S△DOE:S△COA=1:25,∴
∵DE//AC,∴,∴,∴的比是1:4.
2.如图所示,在ABCD中,G是BC延长线上的一点,AG与BD交于点E,与DC交于点F,此图中的相似三角形共有___________对.
解:∵四边形ABCD是平行四边形,∴AD//BC,AB//CD
∴(1)△ABD∽△CDB;(2)△ABE∽△FDE;(3)△AED∽△GEB;
(4)△ABG∽△FCG∽△FDA,可以组成3对相似三角形.∴图形中一共有6对相似三角形.
3.如图,在△ABC中,中线BD、CE相交于点O,连接AO并延长,交BC于点F,求证:F是BC的中点.
证明:连接DE交AF于点G,则DE//BC,DE=BC,∴G为AF中点
∴,,∴BF=FC,即点F是BC的中点
4.在△ABC中,AD是角平分线,求证:.
方法一:过点C?CE//AB交AD延长线于点E,∴∠1=∠3,∴△ABD∽△ECD,∴
∵∠1=∠2,∴∠2=∠3,AC=CE,∴
方法二:设ABC中BC边上的高为h,则,,
过D分别作DEAB,于E,DFAC于F,则,
,又∵1=2,∴DE=DF,∴
5.如图,△ABC为等腰直角三角形,D是直角边BC的中点,E在AB上,且AE:EB=2:1,求证:CE⊥AD.
证明:过点B做BF//AC,交CE延长线于点F,则∠CBF=90°,△AEC∽△BEF
∵AE:EB=2:1,∴BF=AC=BC=CD,又AC=CB,∠ACD=∠CBF=90°
∴△ACD≌△CBF,∴∠1=∠2,∵∠1+∠3=90°,∴∠2+∠3-90°
∴∠4=90°,∴CE⊥AD
模型2
共边共角型
已知:∠
1=∠2
结论:△ACD
∽△ABC
模型分析
上图中,不仅要熟悉模型,还要熟记模型的结论,有时候题目中会给出三角形边的乘积关系或者比例关系,我们要能快速判断题中的相似三角形,模型中由△ACD
∽△ABC进而可以得到:AC2=ADAB
模型实例
例1
如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B,如果△ABD的面积为15.那么△ACD的面积为
.
解答:
∵∠DAC=∠B,∠C=∠C,∴△ACD
∽△BCA.∵AB=4,AD=2,
∴,∴,∵S△ABD=15,∴S△ACD=5
例2
如图,在Rt△ABC中,∠BAC=90o,AD⊥BC于D.
(1)图中有多少对相似三角形?
(2)求证:AB2=BDBC,AC2=CDCB,AD2=BDCD
(3)求证:ABAC=BCAD
解答
(1)三对.分别是:△ABD
∽△CBA;△ACD
∽△BCA;△ABD
∽△CAD
(2)∵△ABD
∽△CBA,∴.∴AB2=BDBC,∵△ACD
∽△BCA
∴.∴AC2=CDCB,∵△ABD
∽△CAD,∴,∴AD2=BCCD
(3),∴ABAC=BCAD
跟踪练习:
1.如图所示,能判定△ABC∽△DAC的有
.
①∠B=∠DAC
②∠BAC=∠ADC
③AC2=DCBC
④AD2=BDBC
【答案】①②③
2.已知△AMN是等边三角形,∠BAC=120o.求证:
(1)AB2=BMBC;
(2)AC2=CNCB;
(3)MN2=BMNC.
【答案】证明:∵∠BAC=120o,∴∠B+∠C=60o.∵△AMN是等边三角形,
∴∠B+∠1=∠AMN=60o,∠C+∠2=∠ANM=60o.∴∠1=∠C,∠2=∠B.
(1)∵∠1=∠C,∠B=∠B,∴△BAM
∽△BCA.∴.∴AB2=BMBC
(2)∵∠2=∠B,∠C=∠C,∴△CAN
∽△CBA.∴.∴AC2=CNCB
(3)∵∠1=∠C,∠2=∠B,∴△BAM
∽△ACN.∴.
∴BMCN=ANAM∵AN=AM=MN,∴AB2=BMBC
3.如图,AB是半圆O的直径,C是半圆上一点,过C作CD⊥AB于D,AC=,AD:DB=4:1.求CD的长.
【答案】连接BC,设AD=4x,则DB=x.∴AB=5x.∵AB是半圆O的直径,∴∠ACB=90o
又∵CD⊥AB.∴△ACD∽△ABC.∴AC2=ADAB,即,解得:x=(舍负).
∴AD=.∴CD=
4.如图①,Rt△ABC中,∠ACB=90o,CD⊥AB,我们可以利用△ABC∽△ACD证明AC2=ADAB,这个结论我们称之为射影定理,结论运用:如图②,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF.
(1)试利用射影定理证明△BOF∽△BED;
(2)若DE=2CE,求OF的长.
【答案】(1)∵四边形ABCD为正方形,∴OC⊥BO,∠BCD=90o.∴BC2=BOBD.
∵CF⊥BE,∴BC2=BFBE.∴BOBD=BFBE.即,
又∵∠OBF=∠EBD,∴△BOF
∽△BED.
(2)∵BC=CD=6,而DE=2CE,∴DE=4,CE=2.在Rt△BCE中,BE==,
在Rt△OBC中,OB=,∵△BOF∽△BED,
∴,即,∴.
模型3
一线三等角型
已知,如图①②③中:∠B=∠ACE=∠D
结论:△ABC∽△CDE
模型分析
如图①,∵∠ACE+∠DCE=∠B+∠A,又∵∠B=∠ACE,∴∠DCE=∠A.
∴△ABC∽△CDE.图②③同理可证△ABC∽△CDE.
在一线三等角的模型中,难点在于当已知三个相等的角的时候,容易忽略隐含的其他相等的角,此模型中的三垂直相似应用较多,当看见该模型的时候,应立刻能看出相应的相似三角形.
模型实例
例1
如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60o,BP=1,CD=.则△ABC的边长为
.
解答
∵△ABC是等边三角形,∴AB=BC=AC,∠B=∠C=60o.∵∠APC=∠B+∠BAP,
即∠APD+∠DPC=∠B+∠BAP,又∵∠APD=∠B=60o,∴∠DPC=∠BAP.
又∵∠B=∠C,∴△PCD∽△ABP.∴.
设AB=x,则PC=x-1,,解得x=3.
例2
如图,∠A=∠B=90o,AB=7,AD=2,BC=3,在边AB上取一点P,使得△PAD与△PBC相似,则这样的P点共有
个.
解答
设AP=,则有PB=AB-AP=7-,当△PDA∽△CPB时,,即,
解得:或,当△PDA∽△PCB时,,即,
解得:,则这样的的点P共有3个.
练习:
1.如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上一动点(不与B、C点重合),∠ADE=45°.
(1)求证:△ABD∽△DCE;
(2)设,,求关于的函数关系式;
(3)当△ADE是等腰三角形时,求AE的长.
1.解答:
(3)当△ADE是等腰三角形时,第一种可能是AD=DE.
当△ADE是等腰三角形时,第二种可能是ED=EA.
即△ADE为等腰直角三角形.
当AD=EA时,点D与点B重合,不合题意,所以舍去.
2.如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=a,DE交AC于点E,且.下列结论:
①△ADE∽△ACD;
②当BD=6时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD等于8或;
④
其中正确的结论是
.(把你认为正确的序号都填上)
2.解答:
故①正确.
故②正确.
(3)当∠AED=900时,由可知:△ADE∽△ACD.
∴
∠ADC=∠AED.
∵
∠AED=900,
∴
∠ADC=900.
即
AD⊥BC.
∵
AB=AC,
∴
BD=CD.
当∠CDE=900时,易得△CDE∽△BAD.
故③正确.
(4)易证△CDE∽△BAD,由②可知BC=16,
故④正确,故答案为:①②③④.
3.如图,已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折叠与边BC交于O,连接AP、OP、OA.
(1)求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1∶4,求边AB的长.
3.解答
模型4
倒数型
条件:AF∥DE∥BC
结论:
模型分析
∵AF∥DE∥BC,
∴△BDE∽△BAF,△ADE∽ABC
∴,.
∴
即
∴(两边同时除以DE)
仔细观察,会发现模型中含有两个A型相似模型,它的结论是由两个A型相似的结论相加而得到的,该模型的练习有助于提高综合能力水平.
模型实例
如图,AF∥BC,AC、BF相交于E,过E作ED∥AF交AB于D.
求证:.
证明:
分别过点C、E、F作直线AB的垂线,垂足分别是K、H、G
则(模型结论).
跟踪练习
如图,在△ABC中,CD⊥AB于点D,正方形EFGH的四个顶点都在△ABC的边上.求证:
答案:1、证明:
方法一:如图①
∵
四边形EFGH是正方形,
∴
EF⊥AB
∵
CD⊥AB,
∴
EF∥CD,
∴
△AEF∽△ACD.
∴
①
∵
EH∥AB,
∴
△CEH∽△CAB
∴
∵
EH=EF,
∴
②
①+②得,
∴
方法二:如图②,构造模型4
过点C作AB的平行线交AH的延长线于点K,
依题意有,CK∥EH∥AB,
∴
∵
∴
CK=CD.
∴
2.正方形ABCD中,以AB为边作等边三角形ABE,连接DE交AC于F,交AB于G,连接BF.求证:
(1)
AF+BF=EF;
(2)
答案:(1)如图①,在EF上截取FH=AF.
∵
∠EAB=600,∠BAD=900,AE=AD,
∴
∠1=∠2=150.
∠3=∠2+∠4=600.
∴
△AFH为等边三角形.
∴
∠EAH=∠BAF.
∴
△EAH≌△BAF.
∴
EH=BF.
∴
AF+BF=FH+EH=EF.
(2),如图②,过点G作GK∥BF交AC于点K.
由①可得∠BFC=600,
∴
AH∥GK∥BF.
∴
由模型4,得
∵
AH=AF,GK=GF,
∴
模型5
与圆有关的简单相似
模型分析
图①中,由同弧所对的圆周角相等,易得△PAC∽△PDB.
图②中,由圆的内接四边形的一个外角等于它的内对角,易得△ABD∽△AEC.
图③中,已知AB切⊙O于点A,如下图,
过A作直径AE,连接DE,则有∠EAD+∠E=900.
又∠BAD+∠EAD=900,∠BAD=∠E=∠C.
从而△BAD∽△BCA.
模型实例
如图,点P在⊙O外,PB交⊙O于A、B两点,PC交⊙O于D、C两点.
求证:PA﹒PB=PD﹒PC.
答案:证明:作直线OP交⊙O于C、D两点,连接BC、AD.
∵
∠B=∠D,∠C=∠A,
∴
△PBC∽△PDA.
∴
∴
PA﹒PB=PD﹒PC=(r+d)(r-d)=
r2-d2
证明:
连接AD、BC.
∵四边形ADCB内接于⊙O,
∴∠1=∠2.
又∵∠P=∠P,
∴△PAD∽△PCB.
∴.
∴.
练习1.如图,P是⊙O内的一点,AB是过点P的一条弦,设圆的半径为,.
求证:.
答案
证明:作直线OP交⊙O于C、D两点,连接BC、AD.
∵∠A=∠D,∠C=∠A,
∴△PBC∽△PDA.
∴.
∴
2.如图,已知AB为⊙O的直径,C、D是半圆的三等分点,延长AC、BD交于点E.
(1)求∠E的度数;
(2)点M为BE上一点,且满足,连接CM,求证:CM是⊙O的切线.
答案
解:
(1)连接OC、OD.
∵C、D是半圆的三等分点,
∴.
∵AB为⊙O的直径,
∴∠AOC=∠COD=∠DOB=60°.
∴OA=OC=OD=OB,
∴△AOC、△DOB为等边三角形.
∴∠EAB=∠EBA=60°.
∴∠E=60°.
(2)连接BC,
∵,
∴.
∵∠E=∠E,
∴△CEM∽△BEC.
∵AB为⊙O的直径,
∴∠ACB=90°.
∴∠ECB=90°,
∴∠EMC=∠ECB=90°.
∵C、D是半圆三等分点,
∴∠AOC=∠DOB=60°,
∴OC∥BE.
∴∠OCM=∠EMC=90°.
∴OC⊥CM.
∴CM为⊙O的切线.
模型6
相似和旋转
如图①,已知DE∥BC,将△ADE绕点A旋转一定的角度,连接BD、CE,得到如图②.
结论:△ABD∽△ACE.
模型分析
∵DE∥BC,
∴,
如图②,∠DAE=∠BAC,
∴∠BAD=∠CAE
∴△ABD∽△ACE.
该模型难度较大,常出现在压轴题中,以直角三角形为背景出题,对学生的综合能力要求较高,考察知识点有相似、旋转、勾股定理、三角函数等,是优等生必须掌握的—种题型.
模型实例
如图,在Rt△ABC中,∠BAC=60°,点P在△ABC内,且,PB=5,PC=2.
求.
解答:
如图,作△ABQ,使得∠QAB=∠PAC,∠ABQ=∠ACP,
则△ABQ∽△ACP.
∴,即.
又∠QAP=∠BAC=60°,
∴△AQP∽△ACB
∴∠APQ=∠ACB=90°.
∴AQ=2AP=,PQ=AP=3.
∴△APQ与△APC的相似比为.
∴.
∴.
∴∠BQP=90°.
过A点作AM∥PQ,延长BQ交AM于点M.
∴AM=PQ,MQ=AP.
∴
故.
练习
1.如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CA
E+∠
CBE=90°,连接BF.
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
解:
(1)∵△ABC和△CEF均为等腰直角三角形.
∴
∴∠ACB=∠ECF=45°.
∴∠ACE=∠BCF.
∴△CAE∽△CBF.
∴∠ACB=∠ECF=45°.
∴∠ACE=∠BCF.
∴△CAE∽△CBF.
(2)∵△CAE∽△CBF,
∴∠CAE=∠CBF,
又∵,AE=2.
∴,∴BF=
又∵∠CAE+∠CBE=90°.
∴∠CBF+∠CBE=90°.
∴∠EBF=90°.
∴.
∴.
∵,
∴.
2.已知,在△ABC中,∠BAC=60°.
(1)如图①.若AB=AC,点P在△ABC内,且∠APC=150°,PA=3,PC=4,把△APC绕着点A顺时针旋转,使点C旋转到点B处,得到△ADB,连接DP.
①依题意补全图1;
②直接写出PB的长;
(2)如图②,若AB=AC,点P在△ABC外,且PA=3,PB=5,PC=4,求∠APC
的度数;
(3)如图③,若AB=2AC,点P在△ABC内,且PA=,PB=5,∠APC=120°,请直接写出PC的长.
解:
(1)如图,由旋转有,AD=AP,BD=PC,∠DAB=∠PAC,
∴∠DAP=∠BAC=60°.
∴△ADP为等边三角形.∴DP=PA=3,∠ADP=60°.
∴∠ADB=∠APC=150°,
∴∠BDP=90°,在Rt△BDP中,BD=4,DP=3.
根据勾股定理得:PB=5.
(2)把△APC绕点A顺时针旋转,使点C与点B重合,得到△ADB,连接PD,
∴△APC≌△ADB.
∴AD=AP=3,DB=PC=4,∠PAC=∠DAB,∠APC=∠2.
∴∠DAP=∠BAC,
∵∠BAC=60°,
∴∠DAP=60°,
∴△DAP是等边三角形.
∴PD=3,∠1=60°,
∴.
∴∠PDB=90°.
∴∠2=30°.
∴∠APC=30°.
(3)作△ABQ,使得∠QAB=∠PAC,∠ABQ=∠ACP,则△ABQ∽△ACP,
∴∠AQB=∠APC=120°.
∵AB=2AC,
∴△ABQ与△ACP的相似比为2.
∴AQ=2AP=2,BQ=2CP,
∠QAP=∠QAB+∠BAP=∠PAC+∠BAP=∠BAC=60°.
取AQ中点D,连接PD,
∵AQ=2AP,∴AD=AP.
∴△APD是等边三角形.∴DP=DQ.
∴∠DPQ=∠DQP=30°.∴∠APQ=90°.
∴PQ=3.∴∠BQP=∠AQB-∠AQP=120°-30°=90°.
根据勾股定理得,.∴.
圆中的辅助线
模型1
连半径构造等腰三角形
已知AB是⊙O的一条弦,连接OA,OB,则∠A=∠B.
模型分析
在圆的相关题目中,不要忽略隐含的已知条件.我们通常可以连接半径构造等腰三角形,
利用等腰三角形的性质及圆中的相关定理,解决角度的计算问题
模型实例
如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,求∠A.
解答:如图,连接OB,∵AB=OC,OC=OB,∴AB=BO.∴∠BOC=∠A.
∴∠EBO=∠BOC+∠A=2∠A.而OB=OE,得∠E=∠EBO=2∠A.
1.如图,AB经过⊙O的圆心,点B在⊙O上,若AD=OB,且∠B=54°.试求∠A的度数.
解答:如图,连接OC、OD.∵∠B=54°,OC=OB,∴∠AOC=2∠B=108°.
又∵AD=OB=OD,∴∠A=∠AOD.∵OC=OD,
∴∠OCA=∠ODC=∠A+∠AOD=2∠A.
∴∠A+∠OCA+∠AOC=∠A+2∠A+108°=180°.
∴∠A=24°.
2.如图,AB是⊙O的直径,弦PQ交AB于M,且PM=MO,求证:则=.
证明:如图,连接OP、OQ.
∵PM=OM,
∴∠P=∠MOP.
∵OP=OQ,
∴∠P=∠Q.
∵∠QMO=2∠MOP,
∴∠BOQ=3∠MOP.
∴∠AOP=∠BOQ.
∴=.
模型2
构造直角三角形
如图①,已知AB是⊙O的直径,点C是圆上一点,连接AC、BC,则∠ACB=90o.
如图②,已知AB是⊙O的一条弦,过点O作OE⊥AB,则OE2+AE2=OA2.
模型分析
(1)
如图①,当图形中含有直径时,构造直径所对的圆周角是解问题的重要思路,在证明有关问题中注意90o的圆周角的构造.
(2)如图②,在解决求弦长、弦心距、半径问题时,在圆中常作弦心距或连接半径作为辅助线,利用弦心距、半径和半弦组成一个直角三角形,再利用勾股定理进行计算.
模型实例
例1
已知⊙O的直径AB和弦CD相交于点E,AE=2,BE=6,∠DEB=60o.求CD的长.
解答:
如图,过O作OF⊥CD于点F,连接OD.∵AB=AE+EB,AE=2,EB=6,
∴AB=8.∴OA=AB=4.∴OE=OA-AE=4-2=2
在Rt△OEF中,∠DEB=60?,OE=2,∴EF=1,OF=.
在Rt△ODF中,,∴.∴.
∵OF⊥CD,∴CD=2DF=
例2
如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45?.
(1)求∠EBC的度数;
(2)求证:BD=CD.
解答
(1)∵AB=AC,∠BAC=45°,
∴∠ABC=∠ACB=67.5°.
∵AB是直径,
∴∠AEB=90°,
∴∠EBC=90°-67.5°=22.5°.
(2)连接AD,
∵AB是直径,
∴∠ADB=90°.
又∵AB=AC,
∴BD=CD(等腰三角形三线合一性质).
练习
1.如图,⊙O的弦AB、CD互相垂直,垂足为E,且AE=5,BE=13,点O到AB的距离为2.求点O到CD距离,线段OE的长即⊙O的半径.
解答:如图,连接OB,过O分别作OM⊥AB于点M,ON⊥CD于点N.
∵AB=AE+BE=5+13=18,
∴AM=AB=9.
又∵OM=2,
∴在Rt△OBM中,
BO===11,
由图知,四边形ONEM是矩形,
∴ON=EM=AM-AE=9-5=4,
∴OE===2.
2.已知,AB和CD是⊙O的两条弦,且AB⊥CD于点H,连接BC、AD,作OE⊥AD于点E.求证:OE=BC.
证明:如图,连接AO并延长交⊙O于点F,连接DF、BD.
∵OE⊥AD,
∴AE=DE.
∵OA=OF,
∴OE是△ADF的中位线.
∴OE=DF.
∵AB⊥CD,
∴∠ABD+∠CDB=90°.
∵AF是直径,
∴∠ADF=90°.
∴∠DAF+∠F=90°.
∵∠ABD=∠F,
∴∠CDB=∠DAF.
∴DF=BC.
∴OE=BC.
3.如图,直径AB=2,AB、CD交于点E且夹角为45°.则CE2+DE2=__________.
解答:如图,过点O作OF⊥CD于点F,连接OD.
设OF=a,DF=b,
则在Rt△OFD中,a2+b2=1.
∴CF=DF=b.
∵∠BED=45°,
∴OF=EF=a.
∴CE2+DE2=(b-a)2+(a+b)2=2(a2+b2)=2.
模型3
与圆的切线有关的辅助线
模型分析
(1)已知切线:连接过切点的半径;如图,已知直线AB是⊙O的切线,点C是切点,连接OC,则OC⊥AB.
(2)证明切线:①当已知直线经过圆上的一点时,连半径,证垂直;
如图,已知过圆上一点C的直线AB,连接OC,证明OC⊥AB,则直线AB是⊙O的切线.
②如果不知直线与圆是否有交点时,作垂直,证明垂线段长度等于半径;
如图,过点O作OC⊥AB,证明OC等于⊙O的半径,则直线AB是⊙O的切线.
模型实例
例1
如图,OA、OB是⊙O的半径,且OA⊥OB,P是OA上任意一点,BP的延长线交⊙O于Q,过Q点的切线交OA的延长线于R.求证:RP=PQ.
证明
连接OQ.
∵OQ=OB,
∴∠OQB=∠OBQ.
∵RQ为⊙O的切线,OA⊥OB,
∴∠BPO=90°-∠OBQ,∠BQR=90°-∠OQB.
∴∠BPO=∠QPB=∠BQR.
∴RP=RQ.
例2
如图,△ABC内接于⊙O,过A点作直线DE,当∠BAE=∠C时,试确定直线DE与⊙O的位置关系,并证明你的结论.
解答
直线DE与⊙O相切,理由如下:
连接AO并延长,交⊙O于点F,连接BF.
∵∠BAE=∠C,∠C=∠F,
∴∠BAE=∠F
∵AF为直径,
∴∠ABF=90°.
∴∠F+∠BAF=90°.
∴∠BAE+∠BAF
∴FA⊥DE.
又∵AO是⊙O的半径,
∴直线DE与⊙O相切.
小猿热搜
1.如图,在△ABC中,以AB为直径的⊙O分别与BC、AC相交于点D、E,BD=CD,过点D作⊙O的切线交AC于点F.求证:DF⊥AC.
证明:如图,连接OD.
∵DF是⊙O的切线,D为切点,
∴OD⊥DF.
∴∠ODF=90°.
∵BD=CD,OA=OB,
∴OD是△ABC的中位线.
∴OD∥AC.
∴∠CFD=∠ODF=90°.
∴DF⊥AC.
2.如图,AB是⊙O的直径,AC是它的切线,CO平分∠ACD.求证:CD是⊙O的切线.
证明:
如图,过O点作OE⊥CD于点E.
∵AC是⊙O的切线,
∴OA⊥AC.
∵CO平分∠ACD,OE⊥CD,
∴OA=OE.
∴CD是⊙O的切线.
3.如图,直线AC与⊙O相交于B、C两点,E是的中点,D是⊙O上一点,若∠EDA=∠AMD.求证:AD是⊙O的切线.
证明:如图,连接OE交BC于点F,连接OD.
∵E是是的中点,
∴OE⊥BC.
∴∠E+∠EMF=90°.
∵∠EDA=∠AMD,∠AMD=∠EMF,
∴∠ADM+∠E=90°.
∵OE=OD,
∴∠E=∠ODE.
∴∠ODE+∠ADM=90°,即∠ODA=90°.
∴OD⊥AD.
∴AD是⊙O的切线.
第十二章
辅助圆
模型1
共端点,等线段模型
如图①,出现“共端点,等线段”时,可利用圆定义构造辅助圆.
如图②,若OA=OB=OC,则A、B、C三点在以O为圆心,OA为半径的圆上.
如图③,常见结论有:∠ACB=∠AOB,∠BAC=∠BOC.
模型分析
∵OA=OB=OC.
∴A、B、C三点到点O的距离相等.
∴A、B、C三点在以O为圆心,OA为半径的圆上.
∵∠ACB是的圆周角,∠AOB是的圆心角,
∴∠ACB=∠AOB.
同理可证∠BAC=∠BOC.
(1)若有共端点的三条线段,可考虑构造辅助圆.
(2)构造辅助圆是方便利用圆的性质快速解决角度问题.
模型实例
如图,△ABC和△ACD都是等腰三角形,AB=AC,AC=AD,连接BD.
求证:∠1+∠2=90°.
证明
证法一:如图①,
∵AB=AC=AD.∴B、C、D在以A为圆心,AB为半径的⊙A上. ∴∠ABC=∠2.
在△BAC中,∵∠BAC+∠ABC+∠2=180°,∴2∠1+2∠2=180°.∴∠1+∠2=90°.
证法二:如图②,
∵AB=AC=AD.∴∠BAC=2∠1.∵AB=AC,
∴B、C、D在以A为圆心,AB为半径的⊙O上.
延长BA与圆A相交于E,连接CE.
∴∠E=∠1.(同弧所对的圆周角相等.)
∵AE=AC,∴∠E=∠ACE.
∵BE为⊙A的直径,∴∠BCE=90°.
∴∠2+∠ACE=90°.∴∠1+∠2=90°.
小猿热搜
1.如图,△ABC为等腰三角形,AB=AC,在△ABC的外侧作直线AP,点B与点
D关于AP轴对称,连接BD、CD,CD与AP交于点E.求证:∠1=∠2.
证明
∵A、D关于AP轴对称,∴AP是BD的垂直平分线.
∴AD=AB,ED=EB.又∵AB=AC.
∴C、B、D在以A为圆心,AB为半径的圆上.
∵ED=EB,∴∠EDB=∠EBD.
∴∠2=2∠EDB.又∵∠1=2∠CDB.
∴∠1=∠2.
2.己知四边形ABCD,AB∥CD,且AB=AC=AD=a,BC=b,且2a>b,求BD的长.
解答
以A为圆心,以a为半径作圆,延长BA交⊙A于E点,连接ED.
∵AB∥CD,∴∠CAB=∠DCA,∠DAE=∠CDA.
∵AC=AD,
∴∠DCA=∠CDA.
∴∠DAE=∠CAB.在△CAB和△DAE中.
∴△CAB≌△DAE.
∴ED=BC=b
∵BE是直径,∴∠EDB=90°.
在Rt△EDB中,ED=b,BE=2a,
∴BD===.
模型2
直角三角形共斜边模型
模型分析
如图①、②,Rt△ABC和Rt△ABD共斜边,取AB中点O,根据直角三角形斜边中线等于斜边一半,可得:OC=OD=OA=OB,
∴A、B、C、D四点共圆.
共斜边的两个直角三角形,同侧或异侧,都会得到四点共圆;
四点共圆后可以根据圆周角定理得到角度相等,完成角度等量关系的转化,是证明角度相等重要的途径之一.
模型实例
例1 如图,AD、BE、CF为△ABC的三条高,H为垂线,问:
图中有多少组四点共圆?
求证:∠ADF=∠ADE.
解答
6组
①C、D、H、E四点共圆,圆心在CH的中点处;
②D、B、F、H四点共圆,圆心在BH的中点处;
③A、E、H、F四点共圆,圆心在AH的中点处;
④C、B、F、E四点共圆,圆心在BC的中点处;
⑤B、A、E、D四点共圆,圆心在AB的中点处;
⑥C、D、F、A四点共圆,圆心在AC的中点处.
(2)如图,由B、D、H、F四点共圆,得∠ADF=∠1.
同理:由A、B、D、E四点共圆,得∠ADE=∠1.
∴∠ADF=∠ADE.
例2 如图,E是正方形ABCD的边AB上的一点,过点E作DE的垂线交∠ABC的外
角平分线于点F,求证:FE=DE.
解答
如图,连接DB、DF.
∵四边形ABCD是正方形,且BF是∠CBA的外角平分线,
∴∠CBF=45°,∠DBC=45°,
∴∠DBF=90°.
又∵∠DEF=90°,
∴D、E、B、F四点共圆.
∴∠DFE=∠DBE=45°(同弧所对的圆周角相等).
∴△DEF是等腰直角三角形.
∴FE=DE.
1.如图,锐角△ABC中,BC.CE是高线,DG⊥CE于G,EF⊥BD于F,求证:
证明:由于Rt△BCE与Rt△BCD共斜边BC,
∴B、C、D、E四点共圆.
∴∠DBC=∠DEG,
同理,Rt∠EDF与Rt△DGE共斜边DE,
∴D、E、F、G四点共圆.
于是∠DEG=∠DFG,
因此,∠DBC=∠DFG.
于是FG∥BC
2.
如图,
BE.CF为△ABC的高,且交于点H,连接AH并延长交于BC于点D,求证:AD⊥BC.
3.如图,等边△PQR内接于正方形ABCD,其中点P,Q,R分别在边AD,AB,DC上,M是QR的中点.求证:不论等边△PQR怎样运动,点M为不动点.
4.如图,已知△ABC中,AH是高,AT是角平分线,且TD⊥AB,TE⊥AC.求证:∠AHD=∠AHE.
补充:
图①
图②
图③
图①
图②
图①
图②
图③
A
B
O
C
D
A
B
O
Q
M
P
A
B
O
D
F
C
E
C
B
O
A
D
E
A
B
C
D
E
O
A
B
C
D
E
H
O
A
B
C
D
E
O
A
B
C
O
R
B
O
Q
A
P
A
B
C
D
E
O
A
B
C
D
E
F
O
A
B
C
D
O
A
B
C
D
E
M
O
TOC
\o
"1-3"
\h
\u
8字模型与飞镖模型
2
角平分线四大模型
11
截长补短辅助线模型
21
手拉手模型
29
三垂直全等模型
36
中考复习专题(将军饮马问题题型归纳)
45
蚂蚁行程
51
中点四大模型
59
半角模型
75
相似模型
82
圆中的辅助线
109
第十二章
辅助圆
120
几何秘籍
8字模型与飞镖模型
模型1:角的8字模型
如图所示,AC、BD相交于点O,连接AD、BC.
结论:∠A+∠D=∠B+∠C.
模型分析
证法一:
∵∠AOB是△AOD的外角,∴∠A+∠D=∠AOB.∵∠AOB是△BOC的外角,
∴∠B+∠C=∠AOB.∴∠A+∠D=∠B+∠C.
证法二:
∵∠A+∠D+∠AOD=180°,∴∠A+∠D=180°-∠AOD.∵∠B+∠C+∠BOC=180°,
∴∠B+∠C=180°-∠BOC.又∵∠AOD=∠BOC,∴∠A+∠D=∠B+∠C.
(1)因为这个图形像数字8,所以我们往往把这个模型称为8字模型.
(2)8字模型往往在几何综合题目中推导角度时用到.
模型实例
观察下列图形,计算角度:
(1)如图①,∠A+∠B+∠C+∠D+∠E=________;
解法一:利用角的8字模型.如图③,连接CD.∵∠BOC是△BOE的外角,
∴∠B+∠E=∠BOC.∵∠BOC是△COD的外角,∴∠1+∠2=∠BOC.
∴∠B+∠E=∠1+∠2.(角的8字模型),∴∠A+∠B+∠ACE+∠ADB+∠E
=∠A+∠ACE+∠ADB+∠1+∠2=∠A+∠ACD+∠ADC=180°.
解法二:如图④,利用三角形外角和定理.∵∠1是△FCE的外角,∴∠1=∠C+∠E.
∵∠2是△GBD的外角,∴∠2=∠B+∠D.
∴∠A+∠B+∠C+∠D+∠E=∠A+∠1+∠2=180°.
(2)如图②,∠A+∠B+∠C+∠D+∠E+∠F=________.
(2)解法一:
如图⑤,利用角的8字模型.∵∠AOP是△AOB的外角,∴∠A+∠B=∠AOP.
∵∠AOP是△OPQ的外角,∴∠1+∠3=∠AOP.∴∠A+∠B=∠1+∠3.①(角的8字模型),同理可证:∠C+∠D=∠1+∠2.②
,∠E+∠F=∠2+∠3.③
由①+②+③得:∠A+∠B+∠C+∠D+∠E+∠F=2(∠1+∠2+∠3)=360°.
解法二:利用角的8字模型.如图⑥,连接DE.∵∠AOE是△AOB的外角,
∴∠A+∠B=∠AOE.∵∠AOE是△OED的外角,∴∠1+∠2=∠AOE.
∴∠A+∠B=∠1+∠2.(角的8字模型)
∴∠A+∠B+∠C+∠ADC+∠FEB+∠F=∠1+∠2+∠C+∠ADC+∠FEB+∠F
=360°.(四边形内角和为360°)
练习:
1.(1)如图①,求:∠CAD+∠B+∠C+∠D+∠E=
;
解:如图,∵∠1=∠B+∠D,∠2=∠C+∠CAD,
∴∠CAD+∠B+∠C+∠D+∠E=∠1+∠2+∠E=180°.
故答案为:180°
解法二:
(2)如图②,求:∠CAD+∠B+∠ACE+∠D+∠E=
.
解:由三角形的外角性质,知∠BAC=∠E+∠ACE,∠EAD=∠B+∠D,
又∵∠BAC+∠CAD+∠EAD=180°,∴∠CAD+∠B+∠ACE+∠D+∠E=180°
解法二:
2.如图,求:∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=
.
解:∵∠G+∠D=∠3,∠F+∠C=∠4,∠E+∠H=∠2,∴∠G+∠D+∠F+∠C+∠E+∠H=∠3+∠4+∠2,
∵∠B+∠2+∠1=180°,∠3+∠5+∠A=180°,∴∠A+∠B+∠2+∠4+∠3=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°
解法二:
模型2:角的飞镖模型
如图所示,有结论:∠D=∠A+∠B+∠C.
模型分析
解法一:如图①,作射线AD.
∵∠3是△ABD的外角,∴∠3=∠B+∠1,∵∠4是△ACD的外角,∴∠4=∠C+∠2
∴∠BDC=∠3+∠4,∴∠BDC=∠B+∠1+∠2+∠C,∴∠BDC=∠BAC+∠B+∠C
解法二:如图②,连接BC.
∵∠2+∠4+∠D=180°,∴∠D=180°-(∠2+∠4)
∵∠1+∠2+∠3+∠4+∠A=180°,∴∠A+∠1+∠3=180°-(∠2+∠4)
∴∠D=∠A+∠1+∠3.
(1)因为这个图形像飞镖,所以我们往往把这个模型称为飞镖模型.
(2)飞镖模型在几何综合题目中推导角度时使用.
模型实例
如图,在四边形ABCD中,AM、CM分别平分∠DAB和∠DCB,AM与CM交于M,探究∠AMC与∠B、∠D间的数量关系.
解答:利用角的飞镖模型
如图所示,连接DM并延长.∵∠3是△AMD的外角,∴∠3=∠1+∠ADM,
∵∠4是△CMD的外角,∴∠4=∠2+∠CDM,∵∠AMC=∠3+∠4
∴∠AMC=∠1+∠ADM+∠CDM+∠2,∴∠AMC=∠1+∠2+∠ADC.(角的飞镖模型)
∵AM、CM分别平分∠DAB和∠DCB,∴,,
∴,∴(四边形内角和360°),∴,∴2∠AMC+∠B-∠ADC=360°.
练习:
1.如图,求∠A+∠B+∠C+∠D+∠E+∠F=
.
【答案】230°
提示:∠C+∠E+∠D=∠EOC=115?.(飞镖模型),∠A+∠B+∠F=∠BOF=115?.
∠A+∠B+∠C+∠D+∠E+∠F=115?+115?=230?
2.如图,求∠A+∠B+∠C+∠D=
.
【答案】220°
提示:如图所示,连接BD.
∠AED=∠A+∠3+∠1,∠BFC=∠2+∠4+∠C,
∠A+∠ABF+∠C+∠CDE=∠A+∠3+∠1+∠2+∠4+∠C=∠AED+∠BFC=220?
模型3
边的“8”字模型
如图所示,AC、BD相交于点O,连接AD、BC.结论AC+BD>AD+BC.
模型分析
∵OA+OD>AD①,
OB+OC>BC②,
由①+②得:
OA+OD+OB+OC>BC+AD
即:AC+BD>AD+BC.
模型实例
如图,四边形ABCD的对角线AC、BD相交于点O。
求证:(1)
AB+BC+CD+AD>AC+BD;
(2)
AB+BC+CD+AD
<2AC+2BD.
证明:(1)∵AB+BC>AC①,
CD+AD>AC②,
AB+AD>BD③,
BC+CD>
BD④
由①+②+③+④得:
2
(AB+BC+CD+AD)>2(AC+BD).
即AB+BC+CD+AD
>AC+BD.
(2)
∵AD
AD+BC<
OA+OD+OB+OC.
∴AD+BC
2AC+2BD.
模型4
边的飞镖模型
如图所示有结论:AB+AC>
BD+CD.
模型分析
如图,延长BD交AC于点E。
∵AB+AC=AB+AE+EC,AB+AE>BE,∴AB+A
C>BE+EC.①
,∵BE+EC=BD+DE+EC,
DE+EC>
CD,∴BE+EC>BD+CD.
②
,由①②可得:AB+AC>BD+CD.
模型实例
如图,点O为三角形内部一点.
求证:(1)
2
(AO+BO+CO)>AB+BC+AC;
(2)
AB+BC+AC>AO+BO+CO.
证明:(1)∵OA+OB>AB①,
OB+OC>BC②,
OC+OA>AC③
由①+②+③得:
2
(AO+BO+CO)>AB+BC+AC
(2)如图,延长BO交AC于点E,
∵AB+AC=AB+AE+EC,
AB+AE>BE,
∴AB+AC>BE+EC.
①
∵BE+EC=BO+OE+EC,
OE+EC>CO,∴BE+EC>BO+CO,②
由①②可得:
AB+AC>BO+CO.③(边的飞镖模型)
同理可得:
AB+BC>OA+OC.④
,BC+AC>OA+OB.⑤
由③+④+⑤得:
2
(AB+BC+AC)>2
(AO+BO+CO).
即
AB+BC+AC>AO+BO+CO.
1.如图,在△ABC中,D、E在BC边上,且BD=CE。求证:AB+AC>AD+AE.
【答案】
证法一:如图①,将AC平移至BF,AD延长线与BF相交于点G,连接DF。
由平移可得AC=BF
,∵AC∥BF
,∴∠ACE=∠BFD
,∵BD=CE
∴△AEC≌△FDB
,∴DF=AE
如图,延长AD交BF于点G,∵AB+BF=AB+BG+GF.
∵AB+BG>AG,
∴AB+BF>AG+GF①
,∵AG+GF=AD+DG+GF,
∵DG+GF>DF,
∴AG+GF>AD+DF②
,由①②可得:AB+BF>AD+DF.(飞镖模型)
∴AB+AC=AB+BF>AD+DF=AD+AE.
∴AB+AC>AD+AE.
证法二:如图②,将AC平移至DF,连接BF
,则AC=DF
,∵AC∥DF,∴∠ACE=∠FDB.
∵BD=CE,∴△AEC≌△FBD.
∴BF=AE.
∵OA+OD>AD①,
OB+OF>BF②
由①+②得:OA+OD+OB+OF>BF+AD.
∴AB+DF>BF+AD.(8字模型)
∴AB+AC=AB+DF>BF+AD=AE+AD.
∴AB+AC>AD+AE.
2.观察图形并探究下列各问题,写出你所观察得到的结论,并说明理由.
(1)如图①,△ABC中,P为边BC一点,请比较BP+PC与AB+AC的大小,并说明理由.
(2)如图②,将(1)中的点P移至△ABC内,请比较△BPC的周长与△ABC的周长的大小,并说明理由.
(3)图③将(2)中的点P变为两个点、,请比较四边形的周长与△ABC的周长的大小,并说明理由.
【答案】
(1)如图①,BP+PC
(2)△BPC的周长小于△ABC的周长。
证明:如图②,延长BP交AC于M。在△ABM中,BP+PM
(3)四边形的周长小于△ABC的周长。
证法一:如图③,分别延长、交于M,由(2)知,BM+CM
证法二:如图④,做直线分别交AB、AC于M、N。在△BM中,
由①+②+③得:∴++
角平分线四大模型
模型1
角平分线的点向两边作垂线
如图,P是∠MON的平分线上一点,过点P作PA⊥OM于点A,PB⊥ON于点B,则PB=PA
模型分析
利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口
模型实例
(1)如图①,在△ABC中,∠C=90°,AD平分∠CAB,BC=6,BD=4,那么点D到直线AB的距离是
解答:如图,过点D作DE⊥AB于点E,∵AD平分∠CAB,∴CD=DE.
∵CB=6,BD=4,∴DE=CD=2,即点D到直线AB的距离是2.
(2)如图②,∠1=∠2,∠3=∠4,求证:AP平分∠BAC
证明:如图,过点P作PD⊥AB于点D,PE⊥BC于点E,PF⊥AC于点F,
∵∠1=∠2,∴PD=PE,∵∠3=∠4,
∴PE=PF,∴PD=PF
又∵PD⊥AB,PF⊥AC,∴AP平分∠BAC(角平分线的判定)
练习
如图,在四边形ABCD中,BC>AB,AD=DC,BD平分∠ABC
,
求证:∠BAD+∠BCD=180°
证明:作DE⊥BC于E,作DF⊥BA的延长线于F,∴∠F=∠DEC=90°,
∵BD平分∠ABC,∴DF=DE,又∵AD=DC,∴△DFA≌DEC,∴∠FAD=∠C
∵∠FAD+∠BAD=180°,∴∠BAD+∠BCD=180°
2.如图,△ABC的外角∠ACD∠的平分线CP与内角∠ABC的平分线BP相交于点P,若∠BPC=40°,则∠CAP=
.
解答:如图所示,作PN⊥BD于N,作PF⊥BA,交BA延长线于F,作PM⊥AC于M
∵BP、CP分别是∠CBA和∠DCA的角平分线,∴∠ABP=∠CBP,∠DCP=∠ACP,
PF=PN=PM,∵∠BAC=∠ACD-∠ABC,∠BPC=∠PCD-∠PBC(外角性质)
∴∠BAC=2∠PCD-2∠PBC=2(∠PCD-∠PBC)=2∠BPC=80°
∴∠CAF=180°-∠BAC=100°,∵PF=PM
∴AP是∠FAC的角平分线,∴∠CAP=∠PAF=50°
模型2
截取构造对称全等
如图,P是∠MON的平分线上的一点,点A是射线OM上任意一点,在ON上截取OB=OA,连接PB,则△OPB≌△OPA
模型分析
利用角平分线图形的对称性,在铁的两边构造对称全等三角形,可以得到对应边,对应角相等,利用对称
性把一些线段或角进行转移,这是经常使用的一种解题技巧
模型实例
(1)如图①所示,在△ABC中,AD是△BAC的外角平分线,P是AD上异于点A的任意一点,试比较PB+PC与AB+AC的大小,并说明理由
解题:PB+PC>AB+AC
证明:在BA的延长线上取点E,
使AE=AB,连接PE,∵AD平分∠CAE
∴∠CAD=∠EAD,在△AEP与△ACP中,∵AE=AB,∠CAD=∠EAD,
AP=AP,∴△AEP≌△ACP
(SAS),∴PE=PC
∵在△PBE中:PB+PE>BE,BE=AB+AE=AB+AC,∴PB+PC>AB+AC
(2)如图②所示,AD是△ABC的内角平分线,其它条件不变,试比较PC-PB与AC-AB的大小,并说明理由
解答:AC-AB>PC-PB
证明:在△ABC中,
在AC上取一点E,使AE=AB
,∴AC-AE=AB-AC=BE
∵AD平分∠BAC
,∴∠EAP=∠BAP
,在△AEP和△ACP中
∴△AEP≌△ABP
(SAS)
,∴PE=PB
,∵在△CPE中
CE>CP-PE
,∴AC-AB>PC-PB
练习
已知,在△ABC中,∠A=2∠B,CD是∠ACB的平分线,AC=16,AD=8,
求线段BC的长
解:如图在BC边上截取CE=AC,连结DE,在△ACD和△ECD中
∴△ACD≌△ECD(SAS)
∴AD=DE
,
∠A=∠1
,∵∠A=2∠B,∴∠1=2∠B,
∵∠1=∠B+∠EDB
,
∴∠B=∠EDB,
∴EBB=ED
,
∴EB=DA=8,BC=EC+BE=AC+DA=16+8=24
在△ABC中,AB=AC,∠A=108°,BD平分∠ABC,
求证:BC=AB+CD
证明:在BC上截取BE=BA,连结DE,∵BD平分∠ABC,BE=AB,BD=BD
∴△ABD≌△EBD(SAS),∴∠DEB=∠A=108°,∴∠DEC=180°-108°=72°
∵AB=AC,∴∠C=∠ABC=(180°-108°)=36°,∴∠EDC=72°
,
∴∠DEC=∠EDC,∴CE=CD
,∴BE+CE=AB+CD,∴BC=AB+CD
3.如图所示,在△ABC中,∠A=100°,∠ABC=40°,BD是∠ABC的平分线,延长BD至E,使DE=AD,求证:BC=AB+CE
证明:在CB上取点F,使得BF=AB,连结DF,∵BD平分∠ABC,BD=BD
∴△ABD≌△FBD,∴DF=AD=DE,∠ADB=∠FDB,∴BD平分∠ABC
∴∠ABD=20°,则∠ADB=180°-20°-100°=60°=∠CDE
∠CDF=180°-∠ADB-∠FDB=60°,∴∠CDF=∠CDE,在△CDE和△CDF中
∴△CDE≌CDF,∴CE=CF,∴BC=BF+FC=AB+CE
模型3
角平分线+垂线构造等腰三角形
如图,P是∠MON的平分线上一点,AP丄OP于P点,延长AP交ON于点.B,则△AOB是等腰三角形.
模型分析
构造此模型可以利用等腰三角形的"三线合一”,也可以得到两个全等的直角三角形.进而得到对应边.对应角相等.这个模型巧妙地把角平分线和三线合一联系了起来.
模型实例
如图.己知等腰直角三角形ABC中,∠A=90°,
AB=AC,
BD平分∠ABC,
C?丄BD.垂足为E.求证:BD=2C?.
解答:如图,延长CE、BA交于点F,∵CE丄BD于E,
∠BAC=90°,∴∠BAD=∠CED.
∴∠ABD=∠ACF.又∵AB=AC,
∠BAD=∠CAF=90°,
∴△ABD≌△ACF.∴
BD=CF.
∵BD平分∠ABC,
∴∠CBE=∠FBE.
又BE=BE,∴△BCE≌△BFE.
∴CE=EF.
∴BD=2CE.
练习
1.如图.在△ABC中.BE是角平分线.AD丄BE.垂足为D.求证:∠2=∠1+∠C.
证明:延长AD交BC于F,∵AD⊥BE,
∴∠ADB=∠BDF=90°,
∵∠ABD=∠FBD,
∴
∠2=∠BFD.
∵∠BFD=∠1+∠C,∴∠2=∠1+∠C.
2.如图.在△ABC中.
∠ABC=3∠C,AD是∠BAC的平分线,
BE丄AD于点E.
求证:.
(2)证明:延长BE交AC于点F.∵AD为∠BAC的角平分线,∴∠BAD=∠CAD.∵AE=AE,
∴∠BAE=∠FAE,则△AEB≌△AEF,∴AB=AF,
BE=EF,
∠
2=∠3.∴AC-AB=AC-AF=FC.
∵∠ABC=3∠C,∴∠2+∠1=∠3+∠1=∠1+∠C+∠1=3∠C.∴2∠1=2∠C
即∠1=∠C
∴BF=FO=2BE.∴
模型4
角平分线+平行线
模型分析
有角平分线时.常过角平分线上一点作角的一边的平行线.
构造等腰三角形.为证明结论提供更多的条件.体现了用平分线与等腰三角形之间的密切关系.
模型实例
解答下列问题:
(1)如图①.△ABC中,EF∥BC,点D在EF上,BD、CD分别平分∠ABC、∠ACB.写出线段EF与BE、CF有什么数量关系?
(2)如图②,BD平分∠ABC,CD平分外角∠ACG.
DE//BC交AB于点E,交AC于点F,线段EF与BE、CF有什么数量关系?并说明理由.
(3)如图③,BD、CD为外角∠CBM、∠BCN的平分线,DE//BC交AB延长线于点E.交AC延长线于点F,直接写出线段EF与BE、CF有什么数关系?
解答:(1)
∵EF//BC,∴∠EDB=∠DBC.∴BD平分∠EBC,∴∠EBD=∠DBC=EDB.
∴EB=ED.
同理:DF=FC.
∴EF=ED+DF=BE+CF.
(2)图②中有EF=BE=CF,BD平分∠BAC,∴∠ABD=∠DBC.又DE//BC、∴∠EDB=∠DBC.
∴DE=EB.同理可证:CF=DF
∴EF=DE-DF=BE-CF.
(3)
EF=BE+CF.
练习
1.如图.
在△ABC中,∠ABC和∠ACB的平分线交于点E.过点E作MN∥BC交AB于M点.
交AC于N点.若BM+CN=9,则线段MN的长为
.
解答:∵∠ABC、∠ACB的平分线相交于点E,∴MBE=∠EBC,∠ECN=∠ECB.∵MN//BC,
∴∠EBC=∠MEB,
∠NEC=∠ECB.
∴∠MBE-∠MEB,
∠NEO=∠ECN.∴BM=ME,
EN=CN.
∴MN=ME+EN,即MN=BM+CN.∵BM+CN=9,∴MN=9.
2.
如图.
在△ABC中,AD平分∠BAC.点E、F分別在BD,AD上,EF∥AB.且DE=CD,求证:EF=AC.
证明:如图,过点C作CM∥AB交AD的延长线于点M,∵AB∥EF,∴CM∥EF.∴∠3=∠4.
∵DE=CD,
∠5=∠6,
∴△DEF≌△DCM.∴EF=CM.
∵AB//CM,∴∠2=∠4.
∵∠1=∠2,
∴∠1=∠4.∴CM=AC.∴EF=AC
3.如图.梯形ABCD中,AD∥BC,点E在CD上,且AE平分∠BAD.BE平分∠ABC.求证:AD=AB-BC.
证明:延长AD、BE交于点F.∵AD∥BC,∴∠2=∠F.
∵∠1=∠2,∴∠1=∠F.∴AB=AF.
∵AE平分∠BAD∴BE=EF.
∵∠DEF=∠CEB,
∴△DEF≌△CEB.∴DF=BC.∴AD=AF-DF=AB-BC.
截长补短辅助线模型
模型:截长补短
如图①,若证明线段AB、CD、EF之间存在EF=AB+CD,可以考虑截长补短法.
截长法:如图②,在EF上截取EG=AB,再证明GF=CD即可.
补短法:如图③,延长AB至H点,使BH=CD,再证明AH=EF即可.
模型分析
截长补短的方法适用于求证线段的和差倍分关系.
截长,指在长线端中截取一段等于已知的线段;补短,指将一条短线端延长,延长部分等于已知线段.
该类题目中常出现等腰三角形、角平分线等关键词句,可以采用截长补短法构造全等三角形来完成证明过程.
模型实例
例1:如图,已知在△ABC中,∠C=2∠B,∠1=∠2
.
求证:AB=AC+CD
.
证法一,截长法:
如图①,在AB上取一点E,使AE=AC,连接DE.
∵AE=AC,∠1=∠2,AD=AD,
∴△ACD≌△AED
,
∴CD=DE,∠C=∠3
.
∵∠C=2∠B,
∴∠3=2∠B=∠4+∠B
,
∴∠4=∠B
,
∴DE=BE
,
∴CD=BE.
∵AB=AE+BE,
∴AB=AC+CD
.
证法二,补短法:
如图②,延长AC到点E,使CE=CD,连接DE
.
∵CE=CD,∴∠4=∠E
.
∵∠3=∠4+∠E,∴∠3=2∠E
.
∵∠3=2∠B,∴∠E=∠B
.
∵∠1=∠2,AD=AD,
∴△EAD≌△BAD,∴AE=AB.
又∵AE=AC+CE,
∴∴AB=AC+CD
.
例2:如图,已知OD平分∠AOB,DC⊥OA于点C,∠A=∠GBD
.
求证:AO+BO=2CO
.
证明:在线段AO上取一点E,使CE=AC,连接DE
.
∵CD=CD,DC⊥OA,
∴△ACD≌△ECD,
∴∠A=∠CED
.
∵∠A=∠GBD
,
∴∠CED=∠GBD
,
∴1800-∠CED=1800-∠GBD
,
∴∠OED=∠OBD
.
∵OD平分∠AOB,
∴∠AOD=∠BOD
.
∵OD=OD,
∴△OED≌△OBD
,
∴OB=OE,
∴AO+BO=AO+OE=OE+2CE+OE=OE+CE+OE+CE=2(CE+OE)=2CO
.
跟踪练习
1.
如图,在△ABC中,∠BAC=600,AD是∠BAC的平分线,且AC=AB+BD
.
求∠ABC的度数
.
【答案】
证法一:补短
延长AB到点E,使BE=BD
.
在△BDE中,
∵BE=BD,∴∠E=∠BDE,
∴∠ABC=∠BDE+∠E=2∠E
.
又∵AC=AB+BD,
∴AC=AB+BE,∴AC=AE
.
∵AD是∠BAC的平分线,∠BAC=600,
∴∠EAD=∠CAD=600÷2=300
.
∵AD=AD,
∴△AED≌△ACD,∴∠E=∠C
.
∵∠ABC=2∠E,∴∠ABC=2∠C
.
∵∠BAC=600,
∴∠ABC+∠C=1800-600=1200,
∴∠ABC=1200,∴∠ABC=800
.
证法二:在AC上取一点F,使AF=AB,连接DF.
∵AD是∠BAC的平分线,
∴∠BAD=∠FAD
.
∵AD=AD,
∴△BAD≌△FAD,
∴∠B=∠AFD,BD=FD
.
∵AC=AB+BD,AC=AF+FC
∴FD=FC
,∴∠FDC=∠C
.
∵∠AFD=∠FDC+∠C,
∴∠B=∠FDC+∠C=2∠C
.
∵∠BAC+∠B+∠C=1800,
∴∠ABC=1200,∴∠ABC=800
.
2.
如图,在△ABC中,∠ABC=600,AD、CE分别平分∠BAC、∠ACB
.
求证:AC=AE+CD
.
【答案】如图,在AC边上取点F,使AE=AF,连接OF
.
∵∠ABC=600,∴∠BAC+∠ACB=1800-∠ABC=1200
.
∵AD、CE分别平分∠BAC、∠ACB,
∴∠OAC=∠OAB=,∠OCA=∠OCB=,
∴∠AOE=∠COD=∠OAC+∠OCA==600,
∴∠AOC=1800-∠AOE=1200
.
∵AE=AF,∠EAO=∠FAO,AO=AO,
∴△AOE≌△AOF(SAS),
∴∠AOF=∠AOE=600,
∴∠COF=∠AOC-∠AOF=600,
∴∠COF=∠COD
.
∵CO=CO,CE平分∠ACB,
∴△COD≌△COF(ASA),
∴CD=CF
.
∵AC=AF+CF,
∴AC=AE+CD,
3.
如图,∠ABC+∠BCD=1800,BE、CE分别平分∠ABC、∠DCB
.求证:AB+CD=BC
.
【答案】证法一:截长
如图①,在BC上取一点F,使BF=AB,连接EF
.
∵∠1=∠ABE,BE=BE,
∴△ABE≌△FBE,∴∠3=∠4
.
∵∠ABC+∠BCD=1800,
BE、CE分别平分∠ABC、∠DCB,
∴∠1+∠2=∠ABC+∠DCB
=×1800=900
,
∴∠BEC=900
,
∴∠4+∠5=900,∠3+∠6=900
.
∵∠3=∠4
,∴∠5=∠6
.
∵CE=CE,
∠2=∠DCE
,
∴△CEF≌△CED,∴CF=CD
.
∵BC=BF+CF,AB=BF,∴AB+CD=BC
证法二:补短
如图②,延长BA到点F,使BF=BC,连接EF
.
∵∠1=∠ABE,BE=BE,
∴△BEF≌△BEC,
∴EF=EC,∠BEC=∠BEF
.
∵∠ABC+∠BCD=1800,
BE、CE分别平分∠ABC、∠DCB,
∴∠1+∠2=∠ABC+∠DCB
=×1800=900
,
∴∠BEC=900
,
∴∠BEF=∠BEC=900,
∴∠BEF+∠BEC=1800,
∴C、E、F三点共线
.
∵AB∥CD,∴∠F=∠FCD
.
∵EF=EC,∠FEA=∠DEC,
∴△AEF≌△DEC,
∴AF=CD
.
∵BF=AB+AF,
∴BC=AB+CD
.
4.
如图,在△ABC中,∠ABC=900,AD平分∠BAC交BC于D,∠C=300,BE⊥AD于点E
.
求证:AC-AB=2BE
.
【答案】延长BE交AC于点M
.
∵BE⊥AD,∴∠AEB=∠AEM=900
.
∵∠3=900-∠1,∠4=900-∠2,∠1=∠2,
∴∠3=∠4,∴AB=AM
.
∵BE⊥AE,∴BM=2BE
.
∵∠ABC=900,∠C=300,
∴∠BAC=600
.
∵AB=AM,∴∠3=∠4=600,
∴∠5=900-∠3=300,
∴∠5=∠C,∴CM=BM,
∴AC-AB=CM=BM=2BE
.
5.
如图,Rt△ACB中,A=BC,AD平分∠BAC交BC于点D,CE⊥AD交AD于点F,交AB于点E
.
求证:AD=2DF+CE
.
【答案】在AD上取一点G,使AG=CE,连接CG
.
∵CE⊥AD,
∴∠AFC=900,∠1+∠ACF=900
.
∵∠2+∠ACF=900,∴∠1=∠2
.
∵AC=BC,AG=CE,
∴△ACG≌△CBE,∴∠3=∠B=450,
∴∠2+∠4=900-∠3=450
.
∵∠2=∠1=∠BAC=22.50,
∴∠4=450-∠2=22.50,
∴∠4=∠2=22.50
.
又∵CF=CF,DG⊥CF,
∴△CDF≌△CGF,∴DF=GF
.
∵AD=AG+DG,∴AD=CE+2DF
.
6.
如图,五边形ABCDE中,AB=AE,BC+DE=CD,∠B+∠E=1800
.
求证:AD平分∠CDE
.
【答案】如图,延长CB到点F,使BF=DE,连接AF、AC
.
∵∠1+∠2=1800,∠E+∠1=1800,∴∠2=∠E
.
∵AB=AE,∠2=∠E,BF=DE,
∴△ABF≌△AED,∴∠F=∠4,AF=AD
.
∵BC+DE=CD,∴BC+BF=CD,即FC=CD
.
又∵AC=AC,∴△ACF≌△ACD,
∴∠F=∠3
.
∵∠F=∠4,
∴∠3=∠4,
∴AD平分∠CDE
.
手拉手模型
模型 手拉手
如图,△ABC是等腰三角形、△ADE是等腰三角形,AB=AC,AD=AE,∠BAC=∠DAE=.
结论:连接BD、CE,则有△BAD≌△CAE.
模型分析
如图①,
∠BAD=∠BAC-∠DAC,∠CAE=∠DAE-∠DAC.
∵∠BAC=∠DAE=,
∴∠BAD=∠CAE.
在△BAD和△CAE中,
图②、图③同理可证.
(1)这个图形是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.
(2)如果把小等腰三角形的腰长看作小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,所以把这个模型称为手拉手模型.
(3)手拉手模型常和旋转结合,在考试中作为几何综合题目出现.
模型实例
例1 如图,△ADC与△EDG都为等腰直角三角形,连接AG、CE,相交于点H,问:
(1)AG与CE是否相等?
(2)AG与CE之间的夹角为多少度?
解答:
(1)AG=CE.理由如下:
∵∠ADG=∠ADC+∠CDG,∠CDE=∠GDE+∠CDG,∠ADC=∠EDG=90°,
∴∠ADG=∠CDE.
在△ADG和△CDE中,
∴△ADE≌△CDE.
∴AG=CE.
(2)∵△ADG≌△CDE,
∴∠DAG=∠DCE.
∵∠COH=∠AOD,
∴∠CHA=∠ADC=90°.
∴AG与CE之间的夹角是90°.
例2 如图,在直线AB的同一侧作△ABD和△BCE,△ABD和△BCE都是等边三角形,连接AE、CD,二者交点为H.
求证:(1)△ABE≌△DBC;
(2)AE=DQ;
(3)∠DHA=60°;
(4)△AGB≌△DFB;
(5)△EGB≌△CFB;
(6)连接GF,GF∥AC;
(7)连接HB,HB平分∠AHC.
证明:(1)∠ABE=120°,∠CBD=120°,
在△ABE和△DBC中,
∴△ABE≌△DBC.
(2)∵△ABE≌△DBC,
∴AE=DC.
(3)△ABE≌△DBC,
∴∠1=∠2.
∴∠DGH=∠AGB.
∴∠DHA=∠4=60°.
(4)∵∠5=180°-∠4-∠CBE=60°,
∴∠4=∠5.
∵△ABE≌△DBC,
∴∠1=∠2.
又∵AB=DB,
∴△AGB≌△DFB(ASA).
(5)同(4)可证△EGB≌△CFB(ASA).
(6)如图①所示,连接GF.
由(4)得,△AGB≌△DFB.
∴BG=BF.
又∵∠5=60°,
∴△BGF是等边三角形.
∴∠3=60°.
∴∠3=∠4.
∴GF∥AC.
(7)如图②所示,过点B作BM⊥DC于M,过点B作BN⊥AE于点N.
∵△ABE≌△DBC,
∴S△ABE=S△DBC.
∴×AE×BN=×CD×BM.
∵AE=CD,
∴BM=BN.
∵点B在∠AHC的平分线上.
∴HB平分∠AHC.
跟踪练习:
1.
在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:BE=BF;
(2)若∠CAE=30°,求∠ACF度数.
答案:
(1)证明:∠ABC=90°.
在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL).
∴BE=BF.
(2)∵AB=CB,∠ABC=90°,
∴∠BAC=∠BCA=45°.
∴∠CAE=30°.
∴∠BAE=45°-30°=15°.
∵Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°.
∴∠ACF=∠BCF+∠BCA=15°+45°=60°.
2.如图,△ABD与△BCE都为等边三角形,连接AE与CD,延长AE交CD于点H.
求证:(1)AE=DC;
(2)∠AHD=60°;
(3)连接HB,HB平分∠AHC.
答案:
(1)∵∠ABE=∠ABD-∠EBD,∠DBC=∠EBC-∠EBD,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC.
在△ABE和△DBC中,
∴△ABE≌△DBC.
∴AE=DC.
(2)∵△ABE≌△DBC
,
∴∠EAB=∠CDB.
又∵∠OAB+∠OBA=∠ODH+∠OHD,
∴∠AHD=∠ABD=60°.
(3)过B作AH、DC的垂线,垂足分别为点M、N.
∵△ABE≌△DBC,
∴S△ABE=S△DBC.
即AE·BM=CD·BN.
又∵AE=CD,
∴BM=BN.
∴HB平分∠AHC.
3.在线段AE同侧作等边△ABC和等边△CDE(∠ACE<120°),点P与点M分别是线段BE和AD的中点.
求证:△CPM是等边三角形.
答案:
证明:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE.
∴∠ACB=∠ECD=60°.
∴∠BCE=∠ACD.
∴△BCE≌△ACD.
∴∠CBE=∠CAD,BE=AD.
又∵点P与点M分别是线段BE和AD的中点,
∴BP=AM.
在△BCP和△ACM中,
∴△BCP≌△ACM.
∴PC=MC,∠BCP=∠ACM.
∴∠PCM=∠ACB=60°.
∴△CPM是等边三角形.
4.
将等腰Rt△ABC和等腰Rt△ADE按图①方式放置,∠A=90°,AD边与AB边重合,AB=2AD=4.将△ADE绕A点逆时针方向旋转一个角度(0°<<180°),BD的延长线交CE于P.
(1)如图②,求明:BD=CE,BD⊥CE;
(2)如图③,在旋转的过程中,当AD⊥BD时,求CP长.
答案:
(1)∵等腰Rt△ABC和等腰Rt△ADE,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°.
∵∠DAB=90°-∠CAD,∠CAE=90°-∠CAD,
∴∠DAB=∠CAE.
∴△ABD≌△ACE.
∴BD=CE.
∴∠DBA=∠ECA.
∴∠CPB=∠CAB.(8字模型)
∴BD⊥CE.
(2)由(1)得BP⊥CE.
又∵AD⊥BD,∠DAE=90°,AD=AE,
∴四边形ADPE为正方形.
∴AD=PE=2.
∴∠ADB=90°,AD=2,AB=4,
∴BD=CE=.
∴CP=CE-PE=.
三垂直全等模型
模型
三垂直全等模型
如图:∠D=∠BCA=∠E=90°,BC=AC.
结论:Rt△BCD≌Rt△CAE.
模型分析
说到三垂直模型,不得不说一下弦图,弦图的运用在初中直角三角形中占有举足轻重的地位,很多利用垂直求角,勾股定理求边长,相似求边长都会用到从弦图支离出来的一部分几何图形去求解.图①和图②就是我们经常会见到的两种弦图.
三垂直图形变形如下图③、图④,这也是由弦图演变而来的.
例1
如图,AB⊥BC,CD⊥BC,AE⊥DE,AE=DE,求证:AB+CD=BC.
证明:∵AE⊥DE,AB⊥BC,DC⊥BC,
∴∠AED=∠B=∠C=90°.
∴∠A+∠AEB=∠AEB+∠CED=90°.
∴∠BAE=∠CED.
在△ABE和△ECD中,
∴△ABE≌△ECD.
∴AB=EC,BE=CD.
∴AB+CD=EC+BE=BC.
例2
如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,BE=0.8cm,则DE的长为多少?
解答:∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°.
∴∠EBC+∠BCE=90°.
∵∠BCE+∠ACD=90°,
∴∠EBC=∠DCA.
在△CEB和△ADC中,
∴△CEB≌△ADC.
∴BE=DC=0.8cm,CE=AD=2.5cm.
∴DE=CE-CD=2.5-0.8=1.7cm.
例3
如图,在平面直角坐标系中,等腰Rt△ABC有两个顶点在坐标轴上,求第三个顶点的坐标.
解答:(1)如图③,过点B作BD⊥x轴于点D.
∴∠BCD+∠DBC=90°.
由等腰Rt△ABC可知,BC=AC,∠ACB=90°,
∴∠BCD+∠ACO=90°.
∴∠DBC=∠ACO.
在△BCD和△CAO中,
∴△BCD≌△CAO.
∴CD=OA,BD=OC.
∵OA=3,OC=2.
∴CD=3,BD=2.
∴OD=5.
∴B(-5,2).
(2)如图④,过点A作AD⊥y轴于点D.
在△ACD和△CBO中,
∴△ACD≌△CBO.
∴CD=OB,AD=CO.
∵B(-1,0),C(0,3)
∴OB=1,OC=3.
∴AD=3,OD=2.
∴OD=5.
∴A(3,2).
跟踪练习
1.如图,正方形ABCD,BE=CF.求证:(1)AE=BF;(2)AE⊥BF.
证明:
(1)∵四边形ABCD是正方形,
∴AB=BD,∠ABC=∠BCD=90°.
在△ABE和△BCF中,
∴△ABE≌△BCF.
∴AE=BF.
(2)∵△ABE≌△BCF.
∴∠BAE=∠CBF.
∵∠ABE=90°,
∴∠BAE+∠AEB=90°.
∴∠CBF+∠AEB=90°.
∴∠BGE=90°,
∴AE⊥BF.
2.直线l上有三个正方形a、b、c,若a、c的面积分别是5和11,则b的面积是_____.
解答:∵a、b、c都是正方形,
∴AC=CD,∠ACD=90°.
∵∠ACB+∠DCE=∠ACB+∠BAC=90°,
∴∠BAC=∠DCE.
在△ABC和△CBE中,
∴△ACB≌△CDE.
∴AB=CE,BC=DE.
在Rt△ABC中,=+=+
即=+=5+11=16.
3.已知,△ABC中,∠BAC=90°,AB=AC,点P为BC上一动点(BP
(2)若P为BC延长线上一点,其它条件不变,则线段BE、CF、EF是否存在某种确定的数量关系?画图并直接写出你的结论.
解答:∵BE⊥AP,CF⊥AP,
∴∠AEB=∠AFC=90°.
∴∠FAC+∠ACF=90°,
∵∠BAC=90°,
∴∠BAE+∠FAC=90°,
∴∠BAE=∠ACF.
在△ABE和△CAF中,
∴△ABE≌△CAF.
∴AE=CF,BE=AF.
∵EF=AE-AF,
∴EF=CF-BE.
(2)如图,EF=BE+CF.
理由:同(1)易证△ABE≌△CAF.
∴AE=CF,BE=AF.
∵EF=AE+AF,
∴EF=
BE
+
CF.
4.如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,设∠BCD=α,以D为旋转中心,将
腰DC绕点D逆时针旋转90°至DE.
(1)当α=45°时,求△EAD的面积;
(2)当α=45°时,求△EAD的面积;
(3)当0°<α<90°,猜想△EAD的面积与α大小有无关系?若有关,写出△EAD的面积S与α的关系式;若无关,请证明结论.
解答:
(1)1;
(2)1;
(3)过点D作DG⊥BC于点G,过点E作EF⊥AD交AD延长线于点F.
∵AD∥BC,DG⊥BC,
∴∠GDF=90°.
又∵∠EDC=90°,
∴∠1=∠2.
在△CGD和△EFD中,
∴△DCG≌△DEF
∴EF=CG,
∵AD∥BC,AB⊥BC,AD=2,BC=3,
∴BG=AD=2,
∴CG=1.
∴=AD·EF=1.
∴△EAD的面积与α大小无关.
5.向△ABC的外侧作正方形ABDE、正方形ACFG,过A作AH⊥BC于H,AH的反向延长线与EG交于点P.
求证:BC=2AP.
解答:过点G作GM⊥AP于点M,过点E作EN⊥AP交AP延长线于点N.
∵四边形ACFG是正方形,
∴AC=AG,∠CAG=90°.
∴∠CAH+∠GAM=90°.
又∵AH⊥BC,
∴∠CAH+∠ACH=90°.
∴∠ACH=∠GAM.
在△ACH和△GAM中,
∴△ACH≌△GAM
∴CH=AM,AH=GM.
同理可证△ABH≌△EAN
∴BH=AN,AH=EN.
∴EN=GM.
在△EPN和△GPM中,
∴△EPN≌△GPM.
∴NP=MP,
∴BC=BH+CH
=AN+AM
=AP+PN+AP-PM
=2AP.
中考复习专题(将军饮马问题题型归纳)
一、求线段和最值
(一)两定一动型
例1:如图,AM⊥EF,BN⊥EF,垂足为M、N,
MN=12m,AM=5m,BN=4m,P是EF上任意一点,则PA+PB的最小值是________
m
分析:这是最基本的将军饮马问题,A、B是定点,P是动点,属于两定一动将军饮马型,根据常见的“定点定线作对称”,可作点A关于EF的对称点A/,根据两点之间,线段最短,连接A/B,此时A/P+PB即为A/B,最短.而要求A/B,则需要构造直角三角形,利用勾股定理解决
解答:
作点A关于EF的对称点A/,过点A作A/C⊥BN的延长线于C.易知A/M=AM=NC=5m,BC=9m,A/C=MN=12m,在Rt△A/BC中,A/B=15m,即PA+PB的最小值是15m
变式:如图,在边长为2的正三角形ABC中,E,F,G为各边中点,P为线段EF上一动点,则△BPG周长的最小值为_________
分析:考虑到BG为定值是1,则△BPG的周长最小转化为求BP+PG的最小值,又是两定一动的将军饮马型,考虑作点G关于EF的对称点,这里有些同学可能看不出来到底是哪个点,我们不妨连接AG,则AG⊥BC,再连接EG,根据“直角三角形斜边中线等于斜边的一半”,可得AE=EG,则点A就是点G关于EF的对称点.最后计算周长时,别忘了加上BG的长度
解答:
连接AG,易知PG=PA,BP+PG=BP+PA,当B,P,A三点共线时,BP+PG=BA,此时最短,BA=2,BG=1,即△BPG周长最短为3
(二)、一定两动型
例2:如图,在△ABC中,AB=AC=5,D为BC中点,AD=5,P为AD上任意一点,E为AC上任意一点,求PC+PE的最小值.
分析:这里的点C是定点,P、E是动点,属于一定两动的将军饮马模型,由于△ABC是等腰三角形,AD是BC中线,则AD垂直平分BC,点C关于AD的对称点是点B,PC+PE=PB+PE,显然当B、P、E三点共线时,BE更短。但此时还不是最短,根据“垂线段最短”只有当BE⊥AC时,BE最短,求BE时,用面积法即可.
解答:
作BE⊥AC交于点E,交AD于点P,易知AD⊥BC,BD=3,BC=6,
则AD·BC=BE·AC,
4×6=BE·5,
BE=4.8
变式:如图,BD平分∠ABC,E,F分别为线段BC,BD上的动点,AB=8,△ABC的周长为20,求EF+CF的最小值__________
分析:
这里的点C是定点,F,E是动点,属于一定两动的将军饮马模型,我们习惯于“定点定线作对称”,但这题这样做,会出现问题.因为点C的对称点C/必然在AB上,但由于BC长度未知,BC/长度也未知,则C/相对的也是不确定点,因此我们这里可以尝试作动点E关于BD的对称点.
解答:
如图,作点E关于BD的对称点E/,连接E/F,则EF=E/F+CF,当E/
、F、C三点共线时,E'F+CF=E'C,此时较短.过点C作CE"⊥AB于E",当,E'与E"重合时,E"C最短,E"C为AB边上的高,E"C=5.
(三)、两点两动型
例3:如图,∠AOB=30°,0C=5,OD=12,点E,F分别是射线OA,OB上的动点,求CF+EF+DE的最小值.
分析:这里的点C,点D是定点,F,E是动点,属于两定两动的将军饮马模型,依旧可以用“定点定线作对称来考虑.作点C关于OB的对称点,点D关于OA的对称点.
解答:作点C关于OB的对称点C′,点D关于0A的对称点D′,连接C′D′.CF+EF+DE=C′F+EF+D′E,当C′,F,E,D′四点共线时,CF+EF+DE=C′D′最短.易知∠D'OC′=90°,OD′=12,OC′=5,C′D'=13,CF+EF+DE最小值为13.
变式:如图,斯诺克比赛桌面AB宽1.78m,白球E距AD边0.22m,距CD边1.4m,有一颗红球F紧贴BC边,且距离CD边0.1m,若要使白球E经过边AD,DC,两次反弹击中红球F,求白球E运动路线的总长度.
分析:本题中,点E和点F是定点,两次反弹的点虽然未知,但我们可以根据前几题的经验作出,即分别作点E关于AD边的对称点E',作点F关于CD边的对称点F',即可画出白球E的运动路线,化归为两定两动将军饮马型.
解答:作点E关于AD边的对称点E′,作点F关于CD边的对称点F′,连接E′F',交AD于点G,交CD于点H,则运动路线长为EG+GH+HF长度之和,即E′F′长,延长E′E交BC于N,交AD于M,易知E′M=EM=0.22m,E′N=1.78+0.22=2m,NF′=NC+CF'=1.4+0.1=1.5m,
则Rt△E′NF′中,E′F′=2.5m,即白球运动路线的总长度为2.5m.
小结:以上求线段和最值问题,几乎都可以归结为“两定一动”、”一定两动”、“两定两动”类的将军饮马型问题,基本方法还是“定点定线作对称”,利用“两点之间线段最短“垂线段最短"的2条重要性质,将线段和转化为直角三角形的斜边,或者一边上的高,借助勾股定理,或者面积法来求解.
当然,有时候,我们也需学会灵活变通,定点对称行不通时,尝试作动点对称.
(二)求角度
例4:P为∠AOB内一定点,M、N分别为射线OA、OB上一
点,当△PMN周长最小时,∠
MPN=80°.
(1)∠AOB=_________°
(2)求证:OP平分∠
MPN
分析:这又是一定两动型将军饮马问题,我们应该先将M,N的位置找到,再来思考∠AOB的度数,显然作点P关于OA的对称点P′,关于OB的对称点P”,连接P′P",其与OA交点即为M,
与OB交点即为N,如下图,易知∠DPC与∠AOB互补,则求出∠DPC的度数即可解答:(1)法1:如图,∠1+∠2=100°,∠1=∠MP′P+∠3=2∠3,∠2=∠NP"P+∠4=2∠4,
则∠3+∠4=50°,∠DPC=130°,∠AOB=50°
再分析:考虑到第二小问要证明OP平分∠MPN,我们就连接OP,则要证∠5=∠6,显然很困难,这时候,考虑到对称性,我们再连接OP',OP",则∠5=∠7,∠6=∠8,问题迎刃而解.
解答:(1)法2易知OP′=0P",∠7+∠8=∠5+∠6=80°,∠P′OP”=100°,由对称性知,∠9=∠11,∠10=∠12,∠AOB=∠9+∠10=50°
(2)由OP′=OP",∠P′OP"=100°知,∠7=∠8=40°∠5=∠6=40°,OP平分∠MPN
变式:如图,在五边形
ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC、DE上分别找一点M、N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为_______
分析:这又是典型的一定两动型将军饮马问题,必然是作A点关于BC、DE的对称点A/、A",连接A/A",与BC、DE的交点即为△AMN周长最小时M、N的位置.
解答:如图
∵∠BAE=136°,
∴∠MA/A+∠NA"A=44°
由对称性知,
∠MAA/=∠MA/A,
∠NAA"=∠NA"A
∠AMN+∠ANM=2∠MA/A+2∠NA"A=88°
本讲思考题:
1.如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为_____
2.如图,在矩形ABCD中
AB=4,AD=3.P为矩形ABCD内一点,若矩形ABCD
面积为△PAB面积的4倍,则点P到A,B两点距离之和PA+PB的最小值为________
蚂蚁行程
模型
立体图形展开的最短路径
模型分析
上图为无底的圆柱体侧面展开图,如图蚂蚁从点A沿圆柱表面爬行一周。到点B的最短路径就是展开图中AB′的长,。做此类题日的关键就是,正确展开立体图形,利用“两点之间线段最短”或“两边之和大于第三边”准确找出最短路径。
模型实例
例1.有一圆柱体油罐,已知油罐底面周长是12m,高AB是5m,要从点A处开始绕油罐一周建造房子,正好到达A点的正上方B处,问梯子最短有
多长?
例2.如图,一直圆锥的母线长为QA=8,底面圆的半径,
若一只小蚂蚁从A点出发,绕圆锥的侧面爬行一周后又回到A点,则蚂蚁爬行的最短
路线长是
。
例3.已知长方体的长、宽、高分别为30cm、20cm、10cm,一只蚂蚁从A处出发到B处觅食,求它所走的最短路径。(结果保留根号)
跟踪练习
1.有一个圆锥体如图,高4cm,底面半径5cm,A处有一蚂蚁,若蚂蚁欲沿侧面爬行到C处,求蚂蚁爬行的最短距离。
2.如图,圆锥体的高为8cm,底面周长为4cm,小蚂蚁在圆柱表面爬行,从A点到B点,路线如图,则最短路程为
。
3.桌上有一个圆柱形无盖玻璃杯,高为12厘米,底面周长18厘米,在杯口内壁离杯口距离3厘米的A处有一滴蜜糖,一只小虫22
杯子外壁,当它正好在蜜糖相对方向离桌面3厘米的B处时,突然发现了蜜糖,问小虫至少爬多少厘米才能到达蜜糖所在的位置。
4.已知O为圆锥顶点,OA、OB为圆锥的母线,C为OB的中点,一只小蚂蚁从点C开始沿圆锥侧面爬行到点A,另一只小蚂蚁也从C点出发绕着圆锥侧面爬行到点B,它们所爬行的最短路线的痕迹如图所示,若沿OA剪开,则得到的圆锥侧面展开图为
(
)
A
B
C
D
5.如图,一只蚂蚁沿着边长为2的正方体表面从点A出发,经过3个面爬行到点B,如果它运动的路径是最短的,则最短距离为
。
6.如图是一个边长为6的正方体木箱,点Q
在上底面的棱上,AQ=2,一只
蚂蚁从P点出发沿木箱表面爬行到点Q,求蚂蚁爬行的最短路线。
7.如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm、3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点的最短路程是多少?
中点四大模型
模型1
倍长中线或类中线(与中点有关的线段)构造全等三角形
模型分析
如图①,AD是△ABC的中线,延长AD至点E使DE=AD,易证:△ADC≌△EDB(SAS).
如图②,D是BC中点,延长FD至点E使DE=FD,易证:△FDB≌△EDC(SAS)
当遇见中线或者中点的时候,可以尝试倍长中线或类中线,构造全等三角形,目的是对已知条件中的线段进行转移.
模型实例
如图,已知在△ABC中,AD是BC边上的中线,E是AD上一点,连接BE并延长交AC于点F,AF=EF,求证:AC=BE.
1.如图,在△ABC中,AB=12,AC=20,求BC边上中线AD的范围.
解:延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC与△EDB中,
,
∴△ADC≌△EDB(SAS),
∴EB=AC=20,
根据三角形的三边关系定理:20-12<AE<20+12,
∴4<AD<16,
故AD的取值范围为4<AD<16.
2.如图,在△ABC中,D是BC的中点,DM⊥DN,如果BM2+CN2=DM2+DN2.
求证:AD2=(AB2+AC2).
证明:如图,过点B作AC的平行线交ND的延长线于E,连ME.
∵BD=DC,
∴ED=DN.
在△BED与△CND中,
∵
∴△BED≌△CND(SAS).
∴BE=NC.
∵∠MDN=90°,
∴MD为EN的中垂线.
∴EM=MN.
∴BM2+BE2=BM2+NC2=MD2+DN2=MN2=EM2,
∴△BEM为直角三角形,∠MBE=90°.
∴∠ABC+∠ACB=∠ABC+∠EBC=90°.
∴∠BAC=90°.
∴AD2=(BC)2=(AB2+AC2).
模型2
已知等腰三角形底边中点,可以考虑与顶点连接用“三线合一”.
模型分析
等腰三角形中有底边中点时,常作底边的中线,利用等腰三角形“三线合一”的性质得到角相等,为解题创造更多的条件,当看见等腰三角形的时候,就应想到:
“边等、角等、三线合一”.
模型实例
如图,在△ABC中,AB=AC=5,BC=6,M为BC的中点,MN⊥AC于点N,求MN的长度.
解答:
连接AM.
∵AB=AC=5,BC=6,点M为BC中点,
∴AM⊥BC,BM=CM=BC=3.
∵AB=5,
∴AM=.
∵MN⊥AC,
∴S△ANC=MC·AM=AC·MN.
即:×3×4=×5×MN.
∴MN=
跟踪练习
1.如图,在△ABC中,AB=AC,D是BC的中点,AE⊥DE,AF⊥DF,且AE=AF,求证:∠EDB=∠FDC.
证明:连结AD,
∵AB=AC,D是BC的中点,
∴AD⊥BC,∠ADB=∠ADC=90°
在Rt△AED与Rt△AFD中,
,
∴Rt△AED≌Rt△AFD.(HL)
∴∠ADE=∠ADF,
∵∠ADB+∠ADC=90°,
∴∠EDB=∠FDC.
2.已知Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC、CB(或它们的延长线)于E、F.
(1)当∠EDF绕D点旋转到DF⊥AC于E时(如图①),求证:S△DEF+S△CEF=S△ABC;
(2)当∠EDF绕D点旋转到DE和AC不垂直时,在图②和图③这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,
S△DEF、S△CEF、S△ABC又有怎样的数量关系?请写出你的猜想,不需要证明.
解:(1)连接CD;如图2所示:
∵AC=BC,∠ACB=90°,D为AB中点,
∴∠B=45°,∠DCE=∠ACB=45°,CD⊥AB,CD=AB=BD,
∴∠DCE=∠B,∠CDB=90°,
∵∠EDF=90°,
∴∠1=∠2,
在△CDE和△BDF中,
,
∴△CDE≌△BDF(ASA),
∴S△DEF+S△CEF=S△ADE+S△BDF=S△ABC;
(2)不成立;S△DEF?S△CEF=S△ABC;理由如下:连接CD,如图3所示:
同(1)得:△DEC≌△DBF,∠DCE=∠DBF=135°
∴S△DEF=S五边形DBFEC,
=S△CFE+S△DBC,
=S△CFE+S△ABC,
∴S△DEF-S△CFE=S△ABC.
∴S△DEF、S△CEF、S△ABC的关系是:S△DEF-S△CEF=S△ABC.
模型3
已知三角形一边的中点,可考虑中位线定理
模型分析
在三角形中,如果有中点,可构造三角形的中位线,利用三角形中位线的性质定理:
DE∥BC,且DE=BC来解题.中位线定理中既有线段之间的位置关系又有数量关系,该模型可以解决角问题,线段之间的倍半、相等及平行问题.
模型实例
如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M,N.求证:∠BME=∠CNE.
解答
如图,连接BD,取BD的中点H,连接HE、HF.
∵E、F分别是BC、AD的中点,
∴FH=AB,FH∥AB,HE=DC,HE∥NC.
又∵AB=CD,
∴HE=HF.
∴∠HFE=∠HEF.
∵FH∥MB,HE∥NC,
∴∠BME=∠HFE,∠CNE=∠FEH.
∴∠BME=∠CNE.
练习:
1.(1)如图1,BD,CE分别是△ABC的外角平分线,过点A作AD⊥BD,AE⊥CE,垂足分别为D,E,连接DE,求证:DE∥BC,DE=(AB+BC+AC);
(2)如图2,BD,CE分别是△ABC的内角平分线,其他条件不变,上述结论是否成立?
(3)如图3,BD是△ABC的内角平分线,CE是△ABC的外角平分线,其他条件不变,DE与BC还平行吗?它与△ABC三边又有怎样的数量关系?请写出你的猜想,并对其中一种情况进行证明.
1.解答
(1)如图①,分别延长AE,AD交BC于H,K.
在△BAD和△BKD中,
∴△BAD≌
△BKD(ASA)
∴AD=KD,AB=KB.
同理可证,AE=HE,AC=HC.
∴DE=HK.
又∵HK=BK+BC+CH=AB+BC+AC.
∴DE=(AB+AC+BC).
(2)猜想结果:图②结论为DE=(AB+AC-BC)
证明:分别延长AE,AD交BC于H,K.
在△BAD和△BKD中
∴△BAD≌△BKD(ASA)
∴AD=KD,AB=KB
同理可证,AE=HE,AC=HC.
∴DE=HK.
又∵HK=BK+CH-BC
=AB+AC-BC
∴DE=(AB+AC-BC)
(3)图③的结论为DE=(BC+AC-AB)
证明:分别延长AE,AD交BC或延长线于H,K.
在△BAD和△BKD中,
∴△BAD
≌△BKD(ASA)
∴AD=KD,AB=KB.
同理可证,AE=HE,AC=HC.
∴DE=KH.
又∵HK=BH-BK
=BC+CH-BK
=BC+AC-AB
∴DE=(BC+AC-AB).
2.问题一:如图①,在四边形ABCD中,AB与CD相交于点O,AB=CD,E,F分别是BC,AD的中点,连接EF,分别交DC,AB于点M,N,判断△OMN的形状,请直接写出结论.
问题二:如图②,在△ABC中,AC>AB,D点在AC上,AB=CD,E,F分别是BC,AD的中点,连接EF并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD的形状并证明.
2.证明
(1)等腰三角形(提示:取AC中点H,连接FH,EH,如图①)
(2)△AGD是直角三角形
如图②,连接BD,取BD的中点H,连接HF,HE.
∵F是AD的中点,
∴HF∥AB,HF=AB.
∴∠1=∠3.
同理,HE∥CD,HE=CD,
∴∠2=∠EFC,
∴AB=CD,
∴HF=HE.
∴∠1=∠2.
∵∠EFC=60°,
∴∠3=∠EFC=∠AFG=60°.
∴△AGF是等边三角形.
∴AF=FG.
∴GF=FD.
∴∠FGD=∠FDG=30°.
∴∠AGD=90°,即△AGD是直角三角形.
模型4
已知直角三角形斜边中点,可以考虑构造斜边中线
模型分析
在直角三角形中,当遇见斜边中点时,经常会作斜边上的中线,利用直角三角形斜边上的中线等于斜边的一半,即CD=AB,来证明线段间的数量关系,而且可以得到两个等腰三角形:△ACD和△BCD,该模型经常会与中位线定理一起综合应用.
模型实例
如图,在△ABC中,BE,CF分别为AC,AB上的高,D为BC的中点,DM⊥
EF于点M,求证:FM=EM.
证明
连接DE,DF.
BE,CF分别为边AC,AB上的高,D为BC的中点,
DF=BC,DE=BC.
DF=DE,即△DEF是等腰三角形.
DM⊥EF,
点M是EF的中点,即FM=EM.
练习:
1.如图,在△ABC中,∠B=2∠C,AD⊥BC于D,M为BC的中点,AB=10,求DM的长度.
1.解答
取AB中点N,连接DN,MN.
在Rt△ADB中,N是斜边AB上的中点,
∴DN=AB=BN=5.
∴∠NDB=∠B.
在△ABC中,M,N分别是BC,AB的中点,
∴MN∥AC
∴∠NMB=∠C,
又∵∠NDB是△NDM的外角,
∴∠NDB=∠NMD+∠DNM.
即∠B=∠NMD+∠DNM=∠C+∠DNM.
又∵∠B=2∠C,
∴∠DNM=∠C=∠NMD.
∴DM=DN.
∴DM=5.
2.已知,△ABD和△ACE都是直角三角形,且∠ABD=∠ACE=90°,连接DE,M为DE的中点,连接MB,MC,求证:MB=MC.
2.证明
延长BM交CE于G,
∵△ABD和△ACE都是直角三角形,
∴CE∥BD.
∴∠BDM=∠GEM.
又∵M是DE中点,即DM=EM,
且∠BMD=∠GME,
∴△BMD
≌△GME.
∴BM=MG.
∴M是BG的中点,
∴在Rt△CBG中,BM=CM.
3.问题1:如图①,三角形ABC中,点D是AB边的中点,AE⊥
BC,BF
⊥AC,垂足分别为点E,F.AE、BF交于点M,连接DE,DF,若DE=kDF,则k的值为
.
问题2:如图②,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC内部,且∠MAC=∠MBC,过点M分别作ME
⊥BC,MF⊥
AC,垂足分别为点E,F,连接DE,DF,求证:DE=DF.
问题3:如图③,若将上面问题2中的条件“CB=CA”变为“CB
≠CA”,其他
条件不变,试探究DE与DF之间的数量关系,并证明你的结论.
3.解答
∵(1)AE⊥BC,BF⊥AC,
∴△AEB和△AFB都是直角三角形,
∵D是AB的中点,
∴DE=AB,DF=AB.
∴DE=DF.
∵DE=KDF,
∴k=1.
(2)∵CB=CA,
∴∠CBA=∠CAB.
∵∠MAC=∠MBC,
∴∠CBA-∠MBC=∠CAB-∠MAC,即∠ABM=∠BAM.
∴AM=BM.
∵ME⊥BC,MF⊥AC,
∴∠MEB=∠MFA=90°.
又∵∠MBE=∠MAF,
∴△MEB
≌△MFA(AAS)
∴BE=AF.
∵D是AB的中点,即BD=AD,
又∵∠DBE=∠DAF,
∴△DBE
≌△DAF(SAS)
∴DE=DF.
(3)DE=DF.
如图,作AM的中点G,BM的中点H,连DG,FG,DH,EH.
∵点D是边AB的中点,
∴DG∥BM,DG=BM.
同理可得:DH∥AM,DH=AM.
∵ME⊥BC于E,H是BM的中点.
∴在Rt△BEM中,HE=BM=BH.
∴∠HBE=∠HEB.
∴∠MHE=2∠HBE.
又∵DG=BM,HE=BM,
∴DG=HE.
同理可得:DH=FG.
∠MGF=2∠MAC.
∵DG∥BM,DH∥GM,
∴四边形DHMG是平行四边形.
∴∠DGM=∠DHM.
∵∠MGF=2∠MAC,
∠MHE=2∠MBC,
∠MBC=∠MAC,
∴∠MGF=∠MHE.
∴∠DGM+∠MGF=∠DHM+∠MHE.
∴∠DGF=∠DHE.
在△DHE与△FGD中
∴△DHE≌
△FGD(SAS)
∴DE=DF.
半角模型
模型概述:
过多边形的某个顶点引两条射线,使这两条射线的夹角为该顶角的一半
思想方式:
通过旋转变换构造全等三角形,实现线段的转化
基本模型:
一、正方形含半角
如图,在正方形ABCD中,E,F分别是BC,CD边上的点,∠EAF=45°,证明以下结论:
⑴EF=BE+DF;
⑵△CEF的周长是正方形边长的2倍;
⑶FA平分∠DFE,EA平分∠BEF;
⑷
【小结】
变式训练1-1
如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45?.
(1)如图(1),试判断EF,BE,DF间的数量关系,并说明理由;
(2)如图(2),若AH⊥EF于点H,试判断线段AH与AB的数量关系,并说明理由。
变式训练1-2
探究:
(1)如图1,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45?,试判断BE、DF与EF三条线段之间的数量关系,直接写出判断结果:___;
(2)如图2,若把(1)问中的条件变为“在四边形ABCD中,AB=AD,∠B+∠D=180?,E、F分别是边BC、CD上的点,且∠EAF=∠BAD”,则(1)问中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;
(3)在(2)问中,若将△AEF绕点A逆时针旋转,当点分别E.?F运动到BC、CD延长线上时,如图3所示,其它条件不变,则(1)问中的结论是否发生变化?若变化,请给出结论并予以证明。
二、等腰直角三角形含半角
如图,等腰Rt△ABC中,∠ACB=90°,AC=BC,过点C作∠DCE=45°,交AB边于D,E两点。
证明:⑴△ACE∽△BDC;
⑵
【小结】
变式训练2-1
如图,等腰Rt△ABC中,∠ACB=90°,AC=BC,过点C作∠DCE=45°,交AB边于D,E两点。
⑴若AD=6,AE=16,则BE=
⑵若AB=12,DE=5,AD<BE,则BE=
⑶若,BD=5,则AE=
变式训练2-2
在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60?,∠BDC=120?,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系。
(1)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是___;此时QL=___;
(2)如图2,点M、N边AB、AC上,且当DM≠DN时,猜想(1)问的两个结论还成立吗?写出你的猜想并加以证明;
(3)如图3,当M、N分别在边AB、CA的延长线上时,若AN=x,则Q=___(用x、L表示).
变式训练2-3
(1)如图1,点E.?F分别是正方形ABCD的边BC、CD上的点,∠EAF=45?,连接EF,
则EF、BE、FD之间的数量关系是:EF=BE+FD.连结BD,交AE、AF于点M、N,且MN、BM、DN满足,请证明这个等量关系;
(2)在△ABC中,AB=AC,点D.?E分别为BC边上的两点。
①如图2,当∠BAC=60?,∠DAE=30?时,BD、DE、EC应满足的等量关系是___;
②如图3,当∠BAC=α,(0?<α<90?),∠DAE=α时,BD、DE、EC应满足的等量关系是___.[参考:】
中考真题
如图,已知△ABC,∠ACB=90?,AC=BC,点E.?F在AB上,∠ECF=45?.
(1)求证:△ACF∽△BEC;
(2)设△ABC的面积为S,求证:AF?BE=2S;
(3)试判断以线段AE、EF、FB为边的三角形的形状并给出证明。
已知:如图,正方形ABCD,BM、DN分别平分正方形的两个外角,且满足∠MAN=45?,连接MN.
(1)若正方形的边长为a,求BM?DN的值。
(2)若以BM,DN,MN为三边围成三角形,试猜想三角形的形状,并证明你的结论。
已知:正方形ABCD中,∠MAN=45?,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.
(1)当∠MAN绕点A旋转到BM≠DN时(图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明。
(2)当∠MAN绕点A旋转到(图3)的位置时,线段BM,DN和MN之间又有怎样的数量关系?证明你的猜想。
(3)若正方形的边长为4,当点N运动到DC边的中点处时,求BM的长。
问题背景:
(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120?,∠B=∠ADC=90?.E,F分别是BC,CD上的点。且∠EAF=60?.探究图中线段BE,EF,FD之间的数量关系。小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是___.
探索延伸:
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180?.E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由。
如图,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30?的A处,舰艇乙在指挥中心南偏东70?的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/时的速度前进,舰艇乙沿北偏东50?的方向以80海里/时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E.?F处,且两舰艇之间的夹角为70?,试求此时两舰艇之间的距离。
问题:如图(1),点E.?F分别在正方形ABCD的边BC、CD上,∠EAF=45?,试判断BE、EF、FD之间的数量关系。
【发现证明】
小聪把△ABE绕点A逆时针旋转90?至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论。
【类比引申】
如图(2),四边形ABCD中,∠BAD≠90?,AB=AD,∠B+∠D=180?,点E.?F分别在边BC、CD上,则当∠EAF与∠BAD满足___关系时,仍有EF=BE+FD.
【探究应用】
如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60?,∠ADC=120?,∠BAD=150?,道路BC、CD上分别有景点E.?F,且AE⊥AD,DF=40()米,现要在E.?F之间修一条笔直道路,求这条道路EF的长
相似模型
模型1:A、8模型
已知∠1=∠2
结论:△ADE∽△ABC
模型分析
如图,在相似三角形的判定中,我们通过做平行线,从而得出A型或8型相似.在做题使,我们也常常关注题目由平行线所产生的相似三角形.
模型实例
【例1】如图,在ABC中,中线AF、BD、CE相交于点O,求证:.
解答:证法一:如图①,连接DE.∵D、E是中点,∴.,DE//BC
∴△EOD∽△COB(8模型)∴.同理:,.
∴.
证法二:如图②,过F作FG//AC交BD于点G,∵F是中点,∴.
∵AD=CD,∴.∵FG//AD,∴△GOF∽△DOA(8模型)
∴.同理,.∴.
【例2】如图,点E、F分别在菱形ABCD的边AB、AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若=2,求的值.
解答:∵四边形ABCD是菱形,∴AB=BC=CD=AD.
设DF=a,则DF=AE=a,AF=EB=2a.∵HD//AB,∴△HFD∽△BFA
∴,∴HD=1.5a,,∴FH=BH
∵HD//EB,∴△DGH∽△EGB,∴,∴
∴BG=HB,∴
跟踪练习:
1.如图,D、E分别是△ABC的边AB、BC上的点,且DE//AC,AE、CD相交于点O,若S△DOE:S△COA=1:25.则S△BDE与S△CDE的比是____________.
解答:∵DE//AC,∴△DOE∽△COA,又S△DOE:S△COA=1:25,∴
∵DE//AC,∴,∴,∴的比是1:4.
2.如图所示,在ABCD中,G是BC延长线上的一点,AG与BD交于点E,与DC交于点F,此图中的相似三角形共有___________对.
解:∵四边形ABCD是平行四边形,∴AD//BC,AB//CD
∴(1)△ABD∽△CDB;(2)△ABE∽△FDE;(3)△AED∽△GEB;
(4)△ABG∽△FCG∽△FDA,可以组成3对相似三角形.∴图形中一共有6对相似三角形.
3.如图,在△ABC中,中线BD、CE相交于点O,连接AO并延长,交BC于点F,求证:F是BC的中点.
证明:连接DE交AF于点G,则DE//BC,DE=BC,∴G为AF中点
∴,,∴BF=FC,即点F是BC的中点
4.在△ABC中,AD是角平分线,求证:.
方法一:过点C?CE//AB交AD延长线于点E,∴∠1=∠3,∴△ABD∽△ECD,∴
∵∠1=∠2,∴∠2=∠3,AC=CE,∴
方法二:设ABC中BC边上的高为h,则,,
过D分别作DEAB,于E,DFAC于F,则,
,又∵1=2,∴DE=DF,∴
5.如图,△ABC为等腰直角三角形,D是直角边BC的中点,E在AB上,且AE:EB=2:1,求证:CE⊥AD.
证明:过点B做BF//AC,交CE延长线于点F,则∠CBF=90°,△AEC∽△BEF
∵AE:EB=2:1,∴BF=AC=BC=CD,又AC=CB,∠ACD=∠CBF=90°
∴△ACD≌△CBF,∴∠1=∠2,∵∠1+∠3=90°,∴∠2+∠3-90°
∴∠4=90°,∴CE⊥AD
模型2
共边共角型
已知:∠
1=∠2
结论:△ACD
∽△ABC
模型分析
上图中,不仅要熟悉模型,还要熟记模型的结论,有时候题目中会给出三角形边的乘积关系或者比例关系,我们要能快速判断题中的相似三角形,模型中由△ACD
∽△ABC进而可以得到:AC2=ADAB
模型实例
例1
如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B,如果△ABD的面积为15.那么△ACD的面积为
.
解答:
∵∠DAC=∠B,∠C=∠C,∴△ACD
∽△BCA.∵AB=4,AD=2,
∴,∴,∵S△ABD=15,∴S△ACD=5
例2
如图,在Rt△ABC中,∠BAC=90o,AD⊥BC于D.
(1)图中有多少对相似三角形?
(2)求证:AB2=BDBC,AC2=CDCB,AD2=BDCD
(3)求证:ABAC=BCAD
解答
(1)三对.分别是:△ABD
∽△CBA;△ACD
∽△BCA;△ABD
∽△CAD
(2)∵△ABD
∽△CBA,∴.∴AB2=BDBC,∵△ACD
∽△BCA
∴.∴AC2=CDCB,∵△ABD
∽△CAD,∴,∴AD2=BCCD
(3),∴ABAC=BCAD
跟踪练习:
1.如图所示,能判定△ABC∽△DAC的有
.
①∠B=∠DAC
②∠BAC=∠ADC
③AC2=DCBC
④AD2=BDBC
【答案】①②③
2.已知△AMN是等边三角形,∠BAC=120o.求证:
(1)AB2=BMBC;
(2)AC2=CNCB;
(3)MN2=BMNC.
【答案】证明:∵∠BAC=120o,∴∠B+∠C=60o.∵△AMN是等边三角形,
∴∠B+∠1=∠AMN=60o,∠C+∠2=∠ANM=60o.∴∠1=∠C,∠2=∠B.
(1)∵∠1=∠C,∠B=∠B,∴△BAM
∽△BCA.∴.∴AB2=BMBC
(2)∵∠2=∠B,∠C=∠C,∴△CAN
∽△CBA.∴.∴AC2=CNCB
(3)∵∠1=∠C,∠2=∠B,∴△BAM
∽△ACN.∴.
∴BMCN=ANAM∵AN=AM=MN,∴AB2=BMBC
3.如图,AB是半圆O的直径,C是半圆上一点,过C作CD⊥AB于D,AC=,AD:DB=4:1.求CD的长.
【答案】连接BC,设AD=4x,则DB=x.∴AB=5x.∵AB是半圆O的直径,∴∠ACB=90o
又∵CD⊥AB.∴△ACD∽△ABC.∴AC2=ADAB,即,解得:x=(舍负).
∴AD=.∴CD=
4.如图①,Rt△ABC中,∠ACB=90o,CD⊥AB,我们可以利用△ABC∽△ACD证明AC2=ADAB,这个结论我们称之为射影定理,结论运用:如图②,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF.
(1)试利用射影定理证明△BOF∽△BED;
(2)若DE=2CE,求OF的长.
【答案】(1)∵四边形ABCD为正方形,∴OC⊥BO,∠BCD=90o.∴BC2=BOBD.
∵CF⊥BE,∴BC2=BFBE.∴BOBD=BFBE.即,
又∵∠OBF=∠EBD,∴△BOF
∽△BED.
(2)∵BC=CD=6,而DE=2CE,∴DE=4,CE=2.在Rt△BCE中,BE==,
在Rt△OBC中,OB=,∵△BOF∽△BED,
∴,即,∴.
模型3
一线三等角型
已知,如图①②③中:∠B=∠ACE=∠D
结论:△ABC∽△CDE
模型分析
如图①,∵∠ACE+∠DCE=∠B+∠A,又∵∠B=∠ACE,∴∠DCE=∠A.
∴△ABC∽△CDE.图②③同理可证△ABC∽△CDE.
在一线三等角的模型中,难点在于当已知三个相等的角的时候,容易忽略隐含的其他相等的角,此模型中的三垂直相似应用较多,当看见该模型的时候,应立刻能看出相应的相似三角形.
模型实例
例1
如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60o,BP=1,CD=.则△ABC的边长为
.
解答
∵△ABC是等边三角形,∴AB=BC=AC,∠B=∠C=60o.∵∠APC=∠B+∠BAP,
即∠APD+∠DPC=∠B+∠BAP,又∵∠APD=∠B=60o,∴∠DPC=∠BAP.
又∵∠B=∠C,∴△PCD∽△ABP.∴.
设AB=x,则PC=x-1,,解得x=3.
例2
如图,∠A=∠B=90o,AB=7,AD=2,BC=3,在边AB上取一点P,使得△PAD与△PBC相似,则这样的P点共有
个.
解答
设AP=,则有PB=AB-AP=7-,当△PDA∽△CPB时,,即,
解得:或,当△PDA∽△PCB时,,即,
解得:,则这样的的点P共有3个.
练习:
1.如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上一动点(不与B、C点重合),∠ADE=45°.
(1)求证:△ABD∽△DCE;
(2)设,,求关于的函数关系式;
(3)当△ADE是等腰三角形时,求AE的长.
1.解答:
(3)当△ADE是等腰三角形时,第一种可能是AD=DE.
当△ADE是等腰三角形时,第二种可能是ED=EA.
即△ADE为等腰直角三角形.
当AD=EA时,点D与点B重合,不合题意,所以舍去.
2.如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=a,DE交AC于点E,且.下列结论:
①△ADE∽△ACD;
②当BD=6时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD等于8或;
④
其中正确的结论是
.(把你认为正确的序号都填上)
2.解答:
故①正确.
故②正确.
(3)当∠AED=900时,由可知:△ADE∽△ACD.
∴
∠ADC=∠AED.
∵
∠AED=900,
∴
∠ADC=900.
即
AD⊥BC.
∵
AB=AC,
∴
BD=CD.
当∠CDE=900时,易得△CDE∽△BAD.
故③正确.
(4)易证△CDE∽△BAD,由②可知BC=16,
故④正确,故答案为:①②③④.
3.如图,已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折叠与边BC交于O,连接AP、OP、OA.
(1)求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1∶4,求边AB的长.
3.解答
模型4
倒数型
条件:AF∥DE∥BC
结论:
模型分析
∵AF∥DE∥BC,
∴△BDE∽△BAF,△ADE∽ABC
∴,.
∴
即
∴(两边同时除以DE)
仔细观察,会发现模型中含有两个A型相似模型,它的结论是由两个A型相似的结论相加而得到的,该模型的练习有助于提高综合能力水平.
模型实例
如图,AF∥BC,AC、BF相交于E,过E作ED∥AF交AB于D.
求证:.
证明:
分别过点C、E、F作直线AB的垂线,垂足分别是K、H、G
则(模型结论).
跟踪练习
如图,在△ABC中,CD⊥AB于点D,正方形EFGH的四个顶点都在△ABC的边上.求证:
答案:1、证明:
方法一:如图①
∵
四边形EFGH是正方形,
∴
EF⊥AB
∵
CD⊥AB,
∴
EF∥CD,
∴
△AEF∽△ACD.
∴
①
∵
EH∥AB,
∴
△CEH∽△CAB
∴
∵
EH=EF,
∴
②
①+②得,
∴
方法二:如图②,构造模型4
过点C作AB的平行线交AH的延长线于点K,
依题意有,CK∥EH∥AB,
∴
∵
∴
CK=CD.
∴
2.正方形ABCD中,以AB为边作等边三角形ABE,连接DE交AC于F,交AB于G,连接BF.求证:
(1)
AF+BF=EF;
(2)
答案:(1)如图①,在EF上截取FH=AF.
∵
∠EAB=600,∠BAD=900,AE=AD,
∴
∠1=∠2=150.
∠3=∠2+∠4=600.
∴
△AFH为等边三角形.
∴
∠EAH=∠BAF.
∴
△EAH≌△BAF.
∴
EH=BF.
∴
AF+BF=FH+EH=EF.
(2),如图②,过点G作GK∥BF交AC于点K.
由①可得∠BFC=600,
∴
AH∥GK∥BF.
∴
由模型4,得
∵
AH=AF,GK=GF,
∴
模型5
与圆有关的简单相似
模型分析
图①中,由同弧所对的圆周角相等,易得△PAC∽△PDB.
图②中,由圆的内接四边形的一个外角等于它的内对角,易得△ABD∽△AEC.
图③中,已知AB切⊙O于点A,如下图,
过A作直径AE,连接DE,则有∠EAD+∠E=900.
又∠BAD+∠EAD=900,∠BAD=∠E=∠C.
从而△BAD∽△BCA.
模型实例
如图,点P在⊙O外,PB交⊙O于A、B两点,PC交⊙O于D、C两点.
求证:PA﹒PB=PD﹒PC.
答案:证明:作直线OP交⊙O于C、D两点,连接BC、AD.
∵
∠B=∠D,∠C=∠A,
∴
△PBC∽△PDA.
∴
∴
PA﹒PB=PD﹒PC=(r+d)(r-d)=
r2-d2
证明:
连接AD、BC.
∵四边形ADCB内接于⊙O,
∴∠1=∠2.
又∵∠P=∠P,
∴△PAD∽△PCB.
∴.
∴.
练习1.如图,P是⊙O内的一点,AB是过点P的一条弦,设圆的半径为,.
求证:.
答案
证明:作直线OP交⊙O于C、D两点,连接BC、AD.
∵∠A=∠D,∠C=∠A,
∴△PBC∽△PDA.
∴.
∴
2.如图,已知AB为⊙O的直径,C、D是半圆的三等分点,延长AC、BD交于点E.
(1)求∠E的度数;
(2)点M为BE上一点,且满足,连接CM,求证:CM是⊙O的切线.
答案
解:
(1)连接OC、OD.
∵C、D是半圆的三等分点,
∴.
∵AB为⊙O的直径,
∴∠AOC=∠COD=∠DOB=60°.
∴OA=OC=OD=OB,
∴△AOC、△DOB为等边三角形.
∴∠EAB=∠EBA=60°.
∴∠E=60°.
(2)连接BC,
∵,
∴.
∵∠E=∠E,
∴△CEM∽△BEC.
∵AB为⊙O的直径,
∴∠ACB=90°.
∴∠ECB=90°,
∴∠EMC=∠ECB=90°.
∵C、D是半圆三等分点,
∴∠AOC=∠DOB=60°,
∴OC∥BE.
∴∠OCM=∠EMC=90°.
∴OC⊥CM.
∴CM为⊙O的切线.
模型6
相似和旋转
如图①,已知DE∥BC,将△ADE绕点A旋转一定的角度,连接BD、CE,得到如图②.
结论:△ABD∽△ACE.
模型分析
∵DE∥BC,
∴,
如图②,∠DAE=∠BAC,
∴∠BAD=∠CAE
∴△ABD∽△ACE.
该模型难度较大,常出现在压轴题中,以直角三角形为背景出题,对学生的综合能力要求较高,考察知识点有相似、旋转、勾股定理、三角函数等,是优等生必须掌握的—种题型.
模型实例
如图,在Rt△ABC中,∠BAC=60°,点P在△ABC内,且,PB=5,PC=2.
求.
解答:
如图,作△ABQ,使得∠QAB=∠PAC,∠ABQ=∠ACP,
则△ABQ∽△ACP.
∴,即.
又∠QAP=∠BAC=60°,
∴△AQP∽△ACB
∴∠APQ=∠ACB=90°.
∴AQ=2AP=,PQ=AP=3.
∴△APQ与△APC的相似比为.
∴.
∴.
∴∠BQP=90°.
过A点作AM∥PQ,延长BQ交AM于点M.
∴AM=PQ,MQ=AP.
∴
故.
练习
1.如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CA
E+∠
CBE=90°,连接BF.
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
解:
(1)∵△ABC和△CEF均为等腰直角三角形.
∴
∴∠ACB=∠ECF=45°.
∴∠ACE=∠BCF.
∴△CAE∽△CBF.
∴∠ACB=∠ECF=45°.
∴∠ACE=∠BCF.
∴△CAE∽△CBF.
(2)∵△CAE∽△CBF,
∴∠CAE=∠CBF,
又∵,AE=2.
∴,∴BF=
又∵∠CAE+∠CBE=90°.
∴∠CBF+∠CBE=90°.
∴∠EBF=90°.
∴.
∴.
∵,
∴.
2.已知,在△ABC中,∠BAC=60°.
(1)如图①.若AB=AC,点P在△ABC内,且∠APC=150°,PA=3,PC=4,把△APC绕着点A顺时针旋转,使点C旋转到点B处,得到△ADB,连接DP.
①依题意补全图1;
②直接写出PB的长;
(2)如图②,若AB=AC,点P在△ABC外,且PA=3,PB=5,PC=4,求∠APC
的度数;
(3)如图③,若AB=2AC,点P在△ABC内,且PA=,PB=5,∠APC=120°,请直接写出PC的长.
解:
(1)如图,由旋转有,AD=AP,BD=PC,∠DAB=∠PAC,
∴∠DAP=∠BAC=60°.
∴△ADP为等边三角形.∴DP=PA=3,∠ADP=60°.
∴∠ADB=∠APC=150°,
∴∠BDP=90°,在Rt△BDP中,BD=4,DP=3.
根据勾股定理得:PB=5.
(2)把△APC绕点A顺时针旋转,使点C与点B重合,得到△ADB,连接PD,
∴△APC≌△ADB.
∴AD=AP=3,DB=PC=4,∠PAC=∠DAB,∠APC=∠2.
∴∠DAP=∠BAC,
∵∠BAC=60°,
∴∠DAP=60°,
∴△DAP是等边三角形.
∴PD=3,∠1=60°,
∴.
∴∠PDB=90°.
∴∠2=30°.
∴∠APC=30°.
(3)作△ABQ,使得∠QAB=∠PAC,∠ABQ=∠ACP,则△ABQ∽△ACP,
∴∠AQB=∠APC=120°.
∵AB=2AC,
∴△ABQ与△ACP的相似比为2.
∴AQ=2AP=2,BQ=2CP,
∠QAP=∠QAB+∠BAP=∠PAC+∠BAP=∠BAC=60°.
取AQ中点D,连接PD,
∵AQ=2AP,∴AD=AP.
∴△APD是等边三角形.∴DP=DQ.
∴∠DPQ=∠DQP=30°.∴∠APQ=90°.
∴PQ=3.∴∠BQP=∠AQB-∠AQP=120°-30°=90°.
根据勾股定理得,.∴.
圆中的辅助线
模型1
连半径构造等腰三角形
已知AB是⊙O的一条弦,连接OA,OB,则∠A=∠B.
模型分析
在圆的相关题目中,不要忽略隐含的已知条件.我们通常可以连接半径构造等腰三角形,
利用等腰三角形的性质及圆中的相关定理,解决角度的计算问题
模型实例
如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,求∠A.
解答:如图,连接OB,∵AB=OC,OC=OB,∴AB=BO.∴∠BOC=∠A.
∴∠EBO=∠BOC+∠A=2∠A.而OB=OE,得∠E=∠EBO=2∠A.
1.如图,AB经过⊙O的圆心,点B在⊙O上,若AD=OB,且∠B=54°.试求∠A的度数.
解答:如图,连接OC、OD.∵∠B=54°,OC=OB,∴∠AOC=2∠B=108°.
又∵AD=OB=OD,∴∠A=∠AOD.∵OC=OD,
∴∠OCA=∠ODC=∠A+∠AOD=2∠A.
∴∠A+∠OCA+∠AOC=∠A+2∠A+108°=180°.
∴∠A=24°.
2.如图,AB是⊙O的直径,弦PQ交AB于M,且PM=MO,求证:则=.
证明:如图,连接OP、OQ.
∵PM=OM,
∴∠P=∠MOP.
∵OP=OQ,
∴∠P=∠Q.
∵∠QMO=2∠MOP,
∴∠BOQ=3∠MOP.
∴∠AOP=∠BOQ.
∴=.
模型2
构造直角三角形
如图①,已知AB是⊙O的直径,点C是圆上一点,连接AC、BC,则∠ACB=90o.
如图②,已知AB是⊙O的一条弦,过点O作OE⊥AB,则OE2+AE2=OA2.
模型分析
(1)
如图①,当图形中含有直径时,构造直径所对的圆周角是解问题的重要思路,在证明有关问题中注意90o的圆周角的构造.
(2)如图②,在解决求弦长、弦心距、半径问题时,在圆中常作弦心距或连接半径作为辅助线,利用弦心距、半径和半弦组成一个直角三角形,再利用勾股定理进行计算.
模型实例
例1
已知⊙O的直径AB和弦CD相交于点E,AE=2,BE=6,∠DEB=60o.求CD的长.
解答:
如图,过O作OF⊥CD于点F,连接OD.∵AB=AE+EB,AE=2,EB=6,
∴AB=8.∴OA=AB=4.∴OE=OA-AE=4-2=2
在Rt△OEF中,∠DEB=60?,OE=2,∴EF=1,OF=.
在Rt△ODF中,,∴.∴.
∵OF⊥CD,∴CD=2DF=
例2
如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45?.
(1)求∠EBC的度数;
(2)求证:BD=CD.
解答
(1)∵AB=AC,∠BAC=45°,
∴∠ABC=∠ACB=67.5°.
∵AB是直径,
∴∠AEB=90°,
∴∠EBC=90°-67.5°=22.5°.
(2)连接AD,
∵AB是直径,
∴∠ADB=90°.
又∵AB=AC,
∴BD=CD(等腰三角形三线合一性质).
练习
1.如图,⊙O的弦AB、CD互相垂直,垂足为E,且AE=5,BE=13,点O到AB的距离为2.求点O到CD距离,线段OE的长即⊙O的半径.
解答:如图,连接OB,过O分别作OM⊥AB于点M,ON⊥CD于点N.
∵AB=AE+BE=5+13=18,
∴AM=AB=9.
又∵OM=2,
∴在Rt△OBM中,
BO===11,
由图知,四边形ONEM是矩形,
∴ON=EM=AM-AE=9-5=4,
∴OE===2.
2.已知,AB和CD是⊙O的两条弦,且AB⊥CD于点H,连接BC、AD,作OE⊥AD于点E.求证:OE=BC.
证明:如图,连接AO并延长交⊙O于点F,连接DF、BD.
∵OE⊥AD,
∴AE=DE.
∵OA=OF,
∴OE是△ADF的中位线.
∴OE=DF.
∵AB⊥CD,
∴∠ABD+∠CDB=90°.
∵AF是直径,
∴∠ADF=90°.
∴∠DAF+∠F=90°.
∵∠ABD=∠F,
∴∠CDB=∠DAF.
∴DF=BC.
∴OE=BC.
3.如图,直径AB=2,AB、CD交于点E且夹角为45°.则CE2+DE2=__________.
解答:如图,过点O作OF⊥CD于点F,连接OD.
设OF=a,DF=b,
则在Rt△OFD中,a2+b2=1.
∴CF=DF=b.
∵∠BED=45°,
∴OF=EF=a.
∴CE2+DE2=(b-a)2+(a+b)2=2(a2+b2)=2.
模型3
与圆的切线有关的辅助线
模型分析
(1)已知切线:连接过切点的半径;如图,已知直线AB是⊙O的切线,点C是切点,连接OC,则OC⊥AB.
(2)证明切线:①当已知直线经过圆上的一点时,连半径,证垂直;
如图,已知过圆上一点C的直线AB,连接OC,证明OC⊥AB,则直线AB是⊙O的切线.
②如果不知直线与圆是否有交点时,作垂直,证明垂线段长度等于半径;
如图,过点O作OC⊥AB,证明OC等于⊙O的半径,则直线AB是⊙O的切线.
模型实例
例1
如图,OA、OB是⊙O的半径,且OA⊥OB,P是OA上任意一点,BP的延长线交⊙O于Q,过Q点的切线交OA的延长线于R.求证:RP=PQ.
证明
连接OQ.
∵OQ=OB,
∴∠OQB=∠OBQ.
∵RQ为⊙O的切线,OA⊥OB,
∴∠BPO=90°-∠OBQ,∠BQR=90°-∠OQB.
∴∠BPO=∠QPB=∠BQR.
∴RP=RQ.
例2
如图,△ABC内接于⊙O,过A点作直线DE,当∠BAE=∠C时,试确定直线DE与⊙O的位置关系,并证明你的结论.
解答
直线DE与⊙O相切,理由如下:
连接AO并延长,交⊙O于点F,连接BF.
∵∠BAE=∠C,∠C=∠F,
∴∠BAE=∠F
∵AF为直径,
∴∠ABF=90°.
∴∠F+∠BAF=90°.
∴∠BAE+∠BAF
∴FA⊥DE.
又∵AO是⊙O的半径,
∴直线DE与⊙O相切.
小猿热搜
1.如图,在△ABC中,以AB为直径的⊙O分别与BC、AC相交于点D、E,BD=CD,过点D作⊙O的切线交AC于点F.求证:DF⊥AC.
证明:如图,连接OD.
∵DF是⊙O的切线,D为切点,
∴OD⊥DF.
∴∠ODF=90°.
∵BD=CD,OA=OB,
∴OD是△ABC的中位线.
∴OD∥AC.
∴∠CFD=∠ODF=90°.
∴DF⊥AC.
2.如图,AB是⊙O的直径,AC是它的切线,CO平分∠ACD.求证:CD是⊙O的切线.
证明:
如图,过O点作OE⊥CD于点E.
∵AC是⊙O的切线,
∴OA⊥AC.
∵CO平分∠ACD,OE⊥CD,
∴OA=OE.
∴CD是⊙O的切线.
3.如图,直线AC与⊙O相交于B、C两点,E是的中点,D是⊙O上一点,若∠EDA=∠AMD.求证:AD是⊙O的切线.
证明:如图,连接OE交BC于点F,连接OD.
∵E是是的中点,
∴OE⊥BC.
∴∠E+∠EMF=90°.
∵∠EDA=∠AMD,∠AMD=∠EMF,
∴∠ADM+∠E=90°.
∵OE=OD,
∴∠E=∠ODE.
∴∠ODE+∠ADM=90°,即∠ODA=90°.
∴OD⊥AD.
∴AD是⊙O的切线.
第十二章
辅助圆
模型1
共端点,等线段模型
如图①,出现“共端点,等线段”时,可利用圆定义构造辅助圆.
如图②,若OA=OB=OC,则A、B、C三点在以O为圆心,OA为半径的圆上.
如图③,常见结论有:∠ACB=∠AOB,∠BAC=∠BOC.
模型分析
∵OA=OB=OC.
∴A、B、C三点到点O的距离相等.
∴A、B、C三点在以O为圆心,OA为半径的圆上.
∵∠ACB是的圆周角,∠AOB是的圆心角,
∴∠ACB=∠AOB.
同理可证∠BAC=∠BOC.
(1)若有共端点的三条线段,可考虑构造辅助圆.
(2)构造辅助圆是方便利用圆的性质快速解决角度问题.
模型实例
如图,△ABC和△ACD都是等腰三角形,AB=AC,AC=AD,连接BD.
求证:∠1+∠2=90°.
证明
证法一:如图①,
∵AB=AC=AD.∴B、C、D在以A为圆心,AB为半径的⊙A上. ∴∠ABC=∠2.
在△BAC中,∵∠BAC+∠ABC+∠2=180°,∴2∠1+2∠2=180°.∴∠1+∠2=90°.
证法二:如图②,
∵AB=AC=AD.∴∠BAC=2∠1.∵AB=AC,
∴B、C、D在以A为圆心,AB为半径的⊙O上.
延长BA与圆A相交于E,连接CE.
∴∠E=∠1.(同弧所对的圆周角相等.)
∵AE=AC,∴∠E=∠ACE.
∵BE为⊙A的直径,∴∠BCE=90°.
∴∠2+∠ACE=90°.∴∠1+∠2=90°.
小猿热搜
1.如图,△ABC为等腰三角形,AB=AC,在△ABC的外侧作直线AP,点B与点
D关于AP轴对称,连接BD、CD,CD与AP交于点E.求证:∠1=∠2.
证明
∵A、D关于AP轴对称,∴AP是BD的垂直平分线.
∴AD=AB,ED=EB.又∵AB=AC.
∴C、B、D在以A为圆心,AB为半径的圆上.
∵ED=EB,∴∠EDB=∠EBD.
∴∠2=2∠EDB.又∵∠1=2∠CDB.
∴∠1=∠2.
2.己知四边形ABCD,AB∥CD,且AB=AC=AD=a,BC=b,且2a>b,求BD的长.
解答
以A为圆心,以a为半径作圆,延长BA交⊙A于E点,连接ED.
∵AB∥CD,∴∠CAB=∠DCA,∠DAE=∠CDA.
∵AC=AD,
∴∠DCA=∠CDA.
∴∠DAE=∠CAB.在△CAB和△DAE中.
∴△CAB≌△DAE.
∴ED=BC=b
∵BE是直径,∴∠EDB=90°.
在Rt△EDB中,ED=b,BE=2a,
∴BD===.
模型2
直角三角形共斜边模型
模型分析
如图①、②,Rt△ABC和Rt△ABD共斜边,取AB中点O,根据直角三角形斜边中线等于斜边一半,可得:OC=OD=OA=OB,
∴A、B、C、D四点共圆.
共斜边的两个直角三角形,同侧或异侧,都会得到四点共圆;
四点共圆后可以根据圆周角定理得到角度相等,完成角度等量关系的转化,是证明角度相等重要的途径之一.
模型实例
例1 如图,AD、BE、CF为△ABC的三条高,H为垂线,问:
图中有多少组四点共圆?
求证:∠ADF=∠ADE.
解答
6组
①C、D、H、E四点共圆,圆心在CH的中点处;
②D、B、F、H四点共圆,圆心在BH的中点处;
③A、E、H、F四点共圆,圆心在AH的中点处;
④C、B、F、E四点共圆,圆心在BC的中点处;
⑤B、A、E、D四点共圆,圆心在AB的中点处;
⑥C、D、F、A四点共圆,圆心在AC的中点处.
(2)如图,由B、D、H、F四点共圆,得∠ADF=∠1.
同理:由A、B、D、E四点共圆,得∠ADE=∠1.
∴∠ADF=∠ADE.
例2 如图,E是正方形ABCD的边AB上的一点,过点E作DE的垂线交∠ABC的外
角平分线于点F,求证:FE=DE.
解答
如图,连接DB、DF.
∵四边形ABCD是正方形,且BF是∠CBA的外角平分线,
∴∠CBF=45°,∠DBC=45°,
∴∠DBF=90°.
又∵∠DEF=90°,
∴D、E、B、F四点共圆.
∴∠DFE=∠DBE=45°(同弧所对的圆周角相等).
∴△DEF是等腰直角三角形.
∴FE=DE.
1.如图,锐角△ABC中,BC.CE是高线,DG⊥CE于G,EF⊥BD于F,求证:
证明:由于Rt△BCE与Rt△BCD共斜边BC,
∴B、C、D、E四点共圆.
∴∠DBC=∠DEG,
同理,Rt∠EDF与Rt△DGE共斜边DE,
∴D、E、F、G四点共圆.
于是∠DEG=∠DFG,
因此,∠DBC=∠DFG.
于是FG∥BC
2.
如图,
BE.CF为△ABC的高,且交于点H,连接AH并延长交于BC于点D,求证:AD⊥BC.
3.如图,等边△PQR内接于正方形ABCD,其中点P,Q,R分别在边AD,AB,DC上,M是QR的中点.求证:不论等边△PQR怎样运动,点M为不动点.
4.如图,已知△ABC中,AH是高,AT是角平分线,且TD⊥AB,TE⊥AC.求证:∠AHD=∠AHE.
补充:
图①
图②
图③
图①
图②
图①
图②
图③
A
B
O
C
D
A
B
O
Q
M
P
A
B
O
D
F
C
E
C
B
O
A
D
E
A
B
C
D
E
O
A
B
C
D
E
H
O
A
B
C
D
E
O
A
B
C
O
R
B
O
Q
A
P
A
B
C
D
E
O
A
B
C
D
E
F
O
A
B
C
D
O
A
B
C
D
E
M
O
同课章节目录
