天津市耀华中学2012届高三寒假验收考试数学文试题 word版
文档属性
| 名称 | 天津市耀华中学2012届高三寒假验收考试数学文试题 word版 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-06 18:22:08 | ||
图片预览




文档简介
天津市耀华中学
2012届高三年级寒假验收考试
数 学 试 题(文)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。共150分,考试用时120分钟。
第I卷(选择题 共40分)
一、选择题:本大题共8小题,每小题5分,共40分,在每小题的4个选项中,只有一项是符合题目要求的,将答案涂在答题卡上。
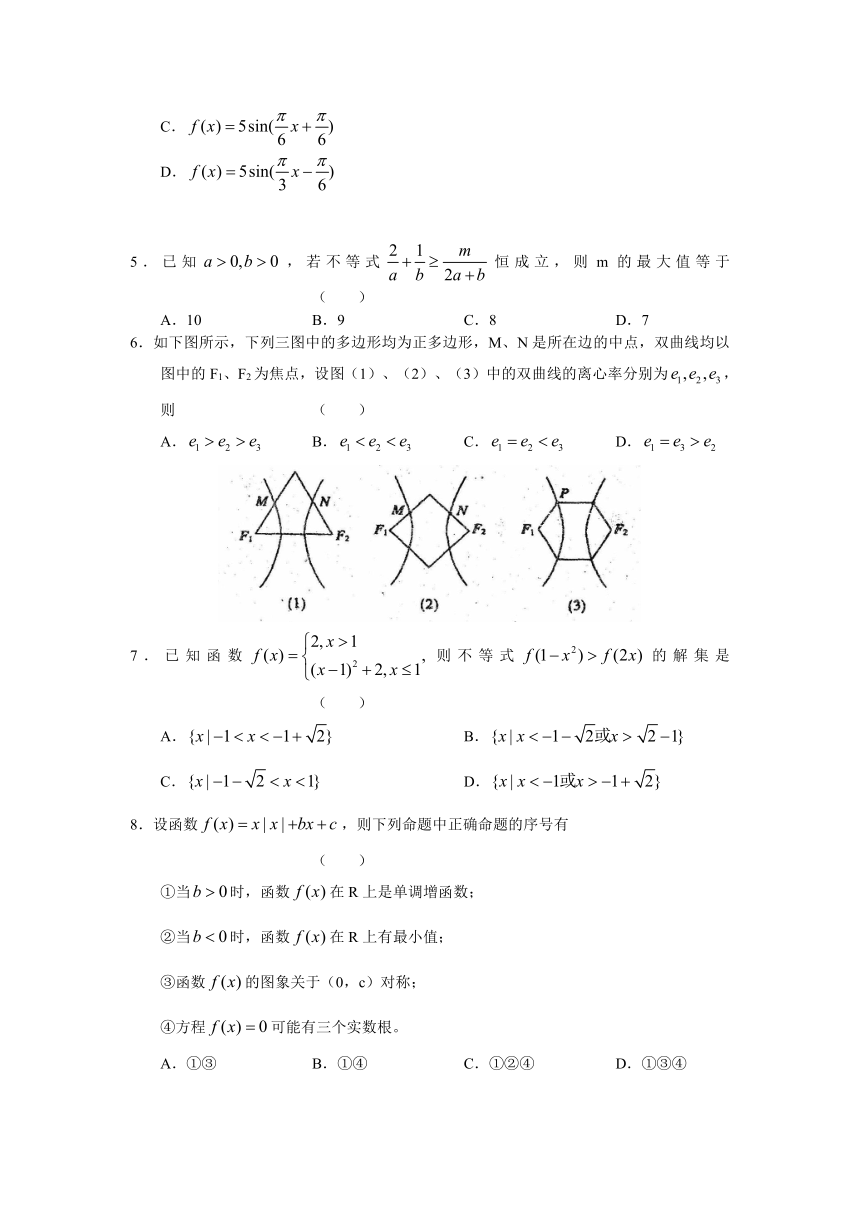
1.已知i是虚数单位,则复数等于 ( )
A.1+i B.1-i C.-1+i D.-1-i
2.阅读程序框图,若输出的S的值等于16,那么在程序
框图中的判断框内应填写的条件是 ( )
A. B.
C. D.
3.已知数成等差数列,-1、b1、b2、-8成等
比数列,则 ( )
A. B.
C. D.
4.已知函数的图象(部分)如图所示,则的解析式是 ( )
A.
B.
C.
D.
5.已知,若不等式恒成立,则m的最大值等于 ( )
A.10 B.9 C.8 D.7
6.如下图所示,下列三图中的多边形均为正多边形,M、N是所在边的中点,双曲线均以图中的F1、F2为焦点,设图(1)、(2)、(3)中的双曲线的离心率分别为,则 ( )
A. B. C. D.
7.已知函数则不等式的解集是 ( )
A. B.
C. D.
8.设函数,则下列命题中正确命题的序号有 ( )
①当时,函数在R上是单调增函数;
②当时,函数在R上有最小值;
③函数的图象关于(0,c)对称;
④方程可能有三个实数根。
A.①③ B.①④ C.①②④ D.①③④
第II卷(非选择题 共110分)
二、填空题:本大题共6小题,每小题5分,共30分,将答案填在答题卡上。
9.若集合,则是 。
10.某工厂生产A、B、C三种不同型号的产品,产品数量之比依次为2:3:5,现用分层抽样方法,抽出一个容量为n的样本,样本中A型号的产品有16件,那么此样本的容量n等于 。
11.已知点是直线上一动点,PA、PB是圆的两条切线,A、B是切点,若四边形PACB的最小面积是2,则k的值为 。
12.已知抛物线的准线为,过点且斜率为的直线与交于点A,与抛物线的一个交点为B,若,则该抛物线的方程为 。
13.如图,四边形OABC是边长为1的正方形,OD=3,点P为
内(含边界)的动点,设其中,
则的最大值等于 。
14.已知等差数列,若,且,则公差d= 。
三、解答题:本题共6小题,共80分,解答应写出必要的文字说明、证明过程或演算步骤。将答案填写在答题卡上。
15.(本小题满分13分)
已知=
(1)求函数的单调增区间;
(2)在中,a、b、c分别为内角A、B、C的对边,且a=1,2,,求的面积。
16.(本小题满分13分)
设有关于x的一元二次方程
(1)若a是从1,2,3,4,5五个数中任取的一个数,b是从0,1,2三个数中任取的一个数, 求上述方程有实根的概率;
(2)若a是从区间[1,5]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率。
17.(本小题满分13分)
如图,四棱锥P—ABCD中,底面ABCD,边四形ABCD是矩形,E、F分别是AB、PD的中点,若
(1)求证:AF//平面PCE;
(2)求点F到平面PCE的距离;
(3)求直线FC与平面PCE所成角的正弦值。
18.(本小题满分13分)
已知椭圆C的焦点坐标分别为,且长轴与焦距的等比中项为。
(1)求椭圆C的标准方程;
(2)已知A(-3,0),B(3,0),P是椭圆C上异于A、B的任意一点,直线AP、BP分别交y轴于M、N,求的值;
(3)在(2)的条件下,若且,分别以OG、OH为边作正方形,求此两正方形的面积和的最小值,并求出取得最小值时的G、H点坐标。
19.(本小题满分14分)
已知函数其中
(1)当a=1时,求曲线在点处切线的倾斜角;
(2)当时,求函数的单调区间;
(3)若,证明对任意,恒成立。
20.(本小题满分14分)
已知,数列,若数列使得2,,成等差数列。
(1)求数列的通项公式;
(2)设,若的前n项和是,且,求证:
数学发展性试题(共15分)
1.已知在半径为2的球面上有A、B、C、D四点,若AB=CD=2,则四面体ABCD的体积的最大值为 。
2.若曲线与曲线有四个不同的交点,则实数m的取值范围是 。
3.设是定义在R上的偶函数,对,均有且,且对,均有,且.数列中,则的通项公式为 。
2012届高三年级寒假验收考试
数 学 试 题(文)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。共150分,考试用时120分钟。
第I卷(选择题 共40分)
一、选择题:本大题共8小题,每小题5分,共40分,在每小题的4个选项中,只有一项是符合题目要求的,将答案涂在答题卡上。
1.已知i是虚数单位,则复数等于 ( )
A.1+i B.1-i C.-1+i D.-1-i
2.阅读程序框图,若输出的S的值等于16,那么在程序
框图中的判断框内应填写的条件是 ( )
A. B.
C. D.
3.已知数成等差数列,-1、b1、b2、-8成等
比数列,则 ( )
A. B.
C. D.
4.已知函数的图象(部分)如图所示,则的解析式是 ( )
A.
B.
C.
D.
5.已知,若不等式恒成立,则m的最大值等于 ( )
A.10 B.9 C.8 D.7
6.如下图所示,下列三图中的多边形均为正多边形,M、N是所在边的中点,双曲线均以图中的F1、F2为焦点,设图(1)、(2)、(3)中的双曲线的离心率分别为,则 ( )
A. B. C. D.
7.已知函数则不等式的解集是 ( )
A. B.
C. D.
8.设函数,则下列命题中正确命题的序号有 ( )
①当时,函数在R上是单调增函数;
②当时,函数在R上有最小值;
③函数的图象关于(0,c)对称;
④方程可能有三个实数根。
A.①③ B.①④ C.①②④ D.①③④
第II卷(非选择题 共110分)
二、填空题:本大题共6小题,每小题5分,共30分,将答案填在答题卡上。
9.若集合,则是 。
10.某工厂生产A、B、C三种不同型号的产品,产品数量之比依次为2:3:5,现用分层抽样方法,抽出一个容量为n的样本,样本中A型号的产品有16件,那么此样本的容量n等于 。
11.已知点是直线上一动点,PA、PB是圆的两条切线,A、B是切点,若四边形PACB的最小面积是2,则k的值为 。
12.已知抛物线的准线为,过点且斜率为的直线与交于点A,与抛物线的一个交点为B,若,则该抛物线的方程为 。
13.如图,四边形OABC是边长为1的正方形,OD=3,点P为
内(含边界)的动点,设其中,
则的最大值等于 。
14.已知等差数列,若,且,则公差d= 。
三、解答题:本题共6小题,共80分,解答应写出必要的文字说明、证明过程或演算步骤。将答案填写在答题卡上。
15.(本小题满分13分)
已知=
(1)求函数的单调增区间;
(2)在中,a、b、c分别为内角A、B、C的对边,且a=1,2,,求的面积。
16.(本小题满分13分)
设有关于x的一元二次方程
(1)若a是从1,2,3,4,5五个数中任取的一个数,b是从0,1,2三个数中任取的一个数, 求上述方程有实根的概率;
(2)若a是从区间[1,5]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率。
17.(本小题满分13分)
如图,四棱锥P—ABCD中,底面ABCD,边四形ABCD是矩形,E、F分别是AB、PD的中点,若
(1)求证:AF//平面PCE;
(2)求点F到平面PCE的距离;
(3)求直线FC与平面PCE所成角的正弦值。
18.(本小题满分13分)
已知椭圆C的焦点坐标分别为,且长轴与焦距的等比中项为。
(1)求椭圆C的标准方程;
(2)已知A(-3,0),B(3,0),P是椭圆C上异于A、B的任意一点,直线AP、BP分别交y轴于M、N,求的值;
(3)在(2)的条件下,若且,分别以OG、OH为边作正方形,求此两正方形的面积和的最小值,并求出取得最小值时的G、H点坐标。
19.(本小题满分14分)
已知函数其中
(1)当a=1时,求曲线在点处切线的倾斜角;
(2)当时,求函数的单调区间;
(3)若,证明对任意,恒成立。
20.(本小题满分14分)
已知,数列,若数列使得2,,成等差数列。
(1)求数列的通项公式;
(2)设,若的前n项和是,且,求证:
数学发展性试题(共15分)
1.已知在半径为2的球面上有A、B、C、D四点,若AB=CD=2,则四面体ABCD的体积的最大值为 。
2.若曲线与曲线有四个不同的交点,则实数m的取值范围是 。
3.设是定义在R上的偶函数,对,均有且,且对,均有,且.数列中,则的通项公式为 。
同课章节目录
