8.4.1平面(22张PPT)
文档属性
| 名称 | 8.4.1平面(22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 00:00:00 | ||
图片预览






文档简介
09人教A版 必修二
7.1复数的概念
8.4 空间点、直线、平面之间的位置关系
8.4.1 平面
前面我们初步认识了简单几何体的组成元素,知道了顶点、棱(直线段)、平面多边形是构成棱柱、棱锥等多面体的基本元素,我们以直观感知的方式认识了这些基本元素之间的相互关系,从而得到了多面体的一些结构特征.为了进一步认识立体图形的结构特征,需要对点、直线、平面之间的位置关系进行研究.本节我们先研究平面及其基本性质,在此基础上,研究空间点、直线、平面之间的位置关系.
在初中,我们已经对点和直线有了一定的认识,知道它们都是由现实事物抽象得到的.生活中也有一些物体给我们以平面的直观感觉,如课桌面、黑板面、平静的水面等.几何里据说的“平面(plane)”就是从这样的一些物体中抽象出来的,类似于直线向两端无限延伸,平面是向四周无限延展的.
平面的基本概念:
平面是一个只描述而不定义的最基本的概念,它是从日常见到的具体的平面抽象出来的理想化的模型.
点评:几何里的平面的特征:
2.无限延展
1.平面是平的
3.不计厚薄
(没有边界)
(没有质量)
A
B
C
D
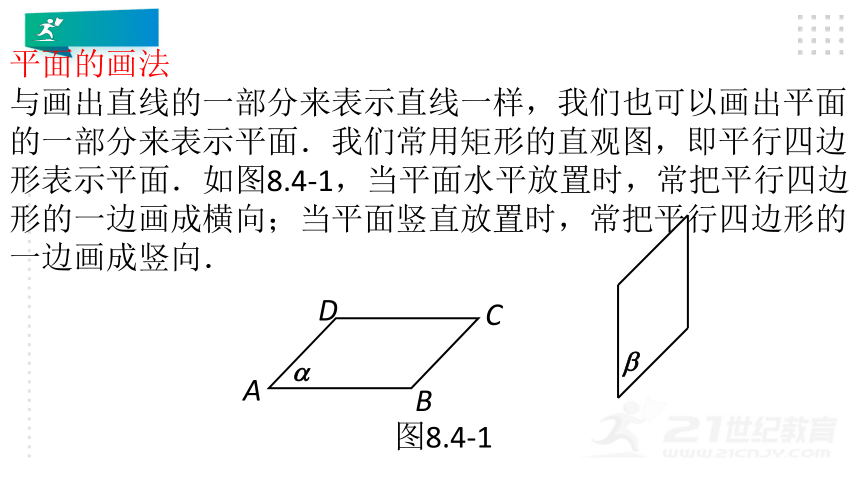
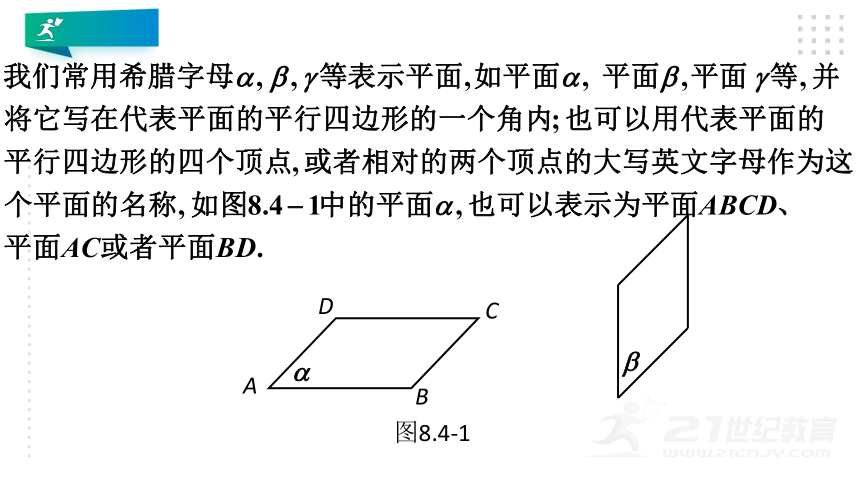
图8.4-1
平面的画法
与画出直线的一部分来表示直线一样,我们也可以画出平面的一部分来表示平面.我们常用矩形的直观图,即平行四边形表示平面.如图8.4-1,当平面水平放置时,常把平行四边形的一边画成横向;当平面竖直放置时,常把平行四边形的一边画成竖向.
A
B
C
D
图8.4-1
下面,我们来研究平面的基本性质.
思考:
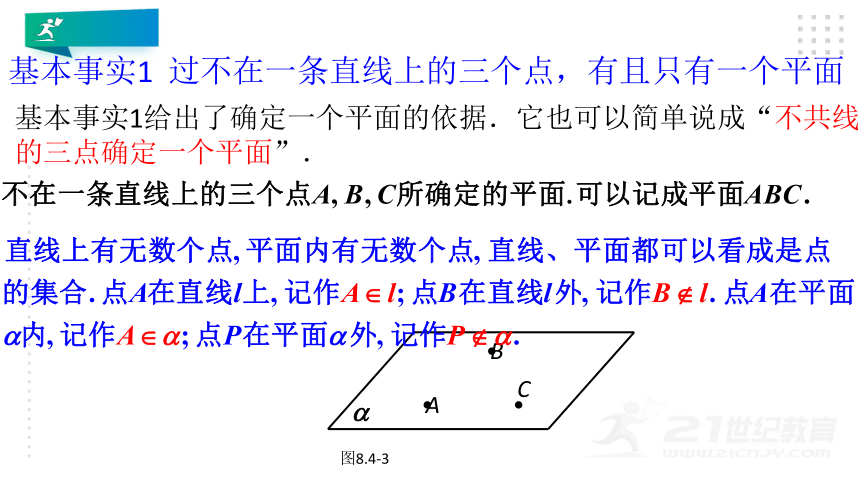
我们知道,两点可以确定一条直线,那么几点可以确定一个平面?
在日常生活中,我们常常可以看到这样的现象:自行车用一个脚架和两个车轮着地就可以“站稳”,三脚架的三脚着地就可以支撑照相机(图8.4-2).由这些事实和类似经验,可以得到下面的基本事实:
A
B
C
图8.4-3
基本事实1 过不在一条直线上的三个点,有且只有一个平面
基本事实1给出了确定一个平面的依据.它也可以简单说成“不共线的三点确定一个平面”.
A
B
l
图8.4-4
在实际生活中,我们有这样的经验:如果一根直尺边缘上的任意两点在桌面上,那么直尺的整个边缘就落在了桌面上.上述经验和类似的事实可以归纳为以下基本事实:
基本事实2 如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
利用基本事实2,可以判断直线是否在平面内.
A
B
l
图8.4-4
基本事实2表明,可以用直线的“直”刻画平面的“平”,用直线的“无限延伸”刻画平面的“无限延展”.如图8.4-5,由基本事实1,给定不共线三点A,B,C,它们可以确定一个平面ABC;连接AB,BC,CA,由基本事实2,这三条直线都在平面ABC内,进而连接这三条直线上任意两点所得直线也都在平面ABC内,所有这些直线可以编织成一个“直线网”,这个“直线网”可以铺满平面ABC.组成这个“直线网”的直线的“直”和向各个方向无限延伸,说明了平面的“平”和“无限延展”.
A
B
C
图8.4-6
如图8.4-6,把三角尺的一个角立在课桌面上,三角尺所在平面与课桌面所在平面是否只相交于一点B?为什么?
想象三角尺所在的无限延展的平面,用它去“穿透”课桌面.可以想象,两个平面相交于一条直线.教室里相邻的墙面在地面的墙角处有一个公共点,这两个墙面相交于这个点的一条直线.由此我们又得到一个基本事实:
B
B
图8.4-7
基本事实3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线
如无特殊说明,本章中的两个平面均指两个不重合的平面.
基本事实3告诉我们,如果两个平面有一个公共点,那么这两个平面一定相交于过这个公共点的一条直线.两个平面相交成一条直线的事实,使我们进一步认识了平面的“平”和“无限延展”.
A
B
A
B
图8.4-8
在画两个相交平面时,如果其中一个平面的一部分被另一个平面挡住,通常把被挡住的部分画成虚线或不画,这样可使画出的图形立体感更强一些(图8.4-8).
上述三个关于平面的基本事实是人们经过长期观察与实践总结出来的,是几何推理的基本依据,也是我们进一步研究立体图形的基础.
(1)
A
B
C
a
(2)
a
b
P
(3)
a
b
图8.4-9
利用基本事实1和基本事实2,再结合“两点确定一条直线”,可以得到下面三个推论(图8.4-9):
推论1 经过一条直线和这条直线外一点,有且只有一个平面.
推论2 经过两条相交直线,有且只有一个平面.
推论3 经过两条平行直线,有且只有一个平面.
(1)
A
B
C
a
推论1~3给我们提供了确定一个平面的另外几种方法.如图8.4-10,用两根细绳沿桌子四条腿的对角拉直,如果这两根细绳相交,说明桌子四条腿的底端在同一个平面内,否则就不在同一个平面内,其依据就是推论2.
不共线的三点,一条直线和这条直线外一点, 两条相交直线,两条平行直线,都能唯一确定一个平面.这些结论在后续研究直线和平面之间平行、 垂直关系时,也会经常用到.
1.判断下列命题是否正确,正确的在括号内画“√”,错误的画“×”.
(1)书桌面是平面. ( )
(2)平面α与平面β相交,它们有有限个公共点. ( )
(3)如果两个平面有三个不共线的公共点,那么这两个平面重合. ( )
(1)× 平面是无限延展的;
(2)× 由基本事实2可知一定有无限个公共点;
(3)√ 由基本事实1可知正确.
×
×
√
2.下列命题正确的是( )
(A)三点确定一个平面
(B)一条直线和一个点确定一个平面
(C)圆心和圆上两点可确定一个平面
(D)梯形可确定一个平面
A错误,因为三点可能共线,也可能不共线;
B错误,因为可能点在直线上,或不在直线上;
C错误,因为圆上两点可能是直径的端点,此时三点共线.
D
P
A
B
C
3.不共面的四点可以确定几个平面?请画出图形说明你的结论.
不共面的四点可以确定4个平面.
A
B
(1)
M
a
a
M
(2)
a
(3)
7.1复数的概念
8.4 空间点、直线、平面之间的位置关系
8.4.1 平面
前面我们初步认识了简单几何体的组成元素,知道了顶点、棱(直线段)、平面多边形是构成棱柱、棱锥等多面体的基本元素,我们以直观感知的方式认识了这些基本元素之间的相互关系,从而得到了多面体的一些结构特征.为了进一步认识立体图形的结构特征,需要对点、直线、平面之间的位置关系进行研究.本节我们先研究平面及其基本性质,在此基础上,研究空间点、直线、平面之间的位置关系.
在初中,我们已经对点和直线有了一定的认识,知道它们都是由现实事物抽象得到的.生活中也有一些物体给我们以平面的直观感觉,如课桌面、黑板面、平静的水面等.几何里据说的“平面(plane)”就是从这样的一些物体中抽象出来的,类似于直线向两端无限延伸,平面是向四周无限延展的.
平面的基本概念:
平面是一个只描述而不定义的最基本的概念,它是从日常见到的具体的平面抽象出来的理想化的模型.
点评:几何里的平面的特征:
2.无限延展
1.平面是平的
3.不计厚薄
(没有边界)
(没有质量)
A
B
C
D
图8.4-1
平面的画法
与画出直线的一部分来表示直线一样,我们也可以画出平面的一部分来表示平面.我们常用矩形的直观图,即平行四边形表示平面.如图8.4-1,当平面水平放置时,常把平行四边形的一边画成横向;当平面竖直放置时,常把平行四边形的一边画成竖向.
A
B
C
D
图8.4-1
下面,我们来研究平面的基本性质.
思考:
我们知道,两点可以确定一条直线,那么几点可以确定一个平面?
在日常生活中,我们常常可以看到这样的现象:自行车用一个脚架和两个车轮着地就可以“站稳”,三脚架的三脚着地就可以支撑照相机(图8.4-2).由这些事实和类似经验,可以得到下面的基本事实:
A
B
C
图8.4-3
基本事实1 过不在一条直线上的三个点,有且只有一个平面
基本事实1给出了确定一个平面的依据.它也可以简单说成“不共线的三点确定一个平面”.
A
B
l
图8.4-4
在实际生活中,我们有这样的经验:如果一根直尺边缘上的任意两点在桌面上,那么直尺的整个边缘就落在了桌面上.上述经验和类似的事实可以归纳为以下基本事实:
基本事实2 如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
利用基本事实2,可以判断直线是否在平面内.
A
B
l
图8.4-4
基本事实2表明,可以用直线的“直”刻画平面的“平”,用直线的“无限延伸”刻画平面的“无限延展”.如图8.4-5,由基本事实1,给定不共线三点A,B,C,它们可以确定一个平面ABC;连接AB,BC,CA,由基本事实2,这三条直线都在平面ABC内,进而连接这三条直线上任意两点所得直线也都在平面ABC内,所有这些直线可以编织成一个“直线网”,这个“直线网”可以铺满平面ABC.组成这个“直线网”的直线的“直”和向各个方向无限延伸,说明了平面的“平”和“无限延展”.
A
B
C
图8.4-6
如图8.4-6,把三角尺的一个角立在课桌面上,三角尺所在平面与课桌面所在平面是否只相交于一点B?为什么?
想象三角尺所在的无限延展的平面,用它去“穿透”课桌面.可以想象,两个平面相交于一条直线.教室里相邻的墙面在地面的墙角处有一个公共点,这两个墙面相交于这个点的一条直线.由此我们又得到一个基本事实:
B
B
图8.4-7
基本事实3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线
如无特殊说明,本章中的两个平面均指两个不重合的平面.
基本事实3告诉我们,如果两个平面有一个公共点,那么这两个平面一定相交于过这个公共点的一条直线.两个平面相交成一条直线的事实,使我们进一步认识了平面的“平”和“无限延展”.
A
B
A
B
图8.4-8
在画两个相交平面时,如果其中一个平面的一部分被另一个平面挡住,通常把被挡住的部分画成虚线或不画,这样可使画出的图形立体感更强一些(图8.4-8).
上述三个关于平面的基本事实是人们经过长期观察与实践总结出来的,是几何推理的基本依据,也是我们进一步研究立体图形的基础.
(1)
A
B
C
a
(2)
a
b
P
(3)
a
b
图8.4-9
利用基本事实1和基本事实2,再结合“两点确定一条直线”,可以得到下面三个推论(图8.4-9):
推论1 经过一条直线和这条直线外一点,有且只有一个平面.
推论2 经过两条相交直线,有且只有一个平面.
推论3 经过两条平行直线,有且只有一个平面.
(1)
A
B
C
a
推论1~3给我们提供了确定一个平面的另外几种方法.如图8.4-10,用两根细绳沿桌子四条腿的对角拉直,如果这两根细绳相交,说明桌子四条腿的底端在同一个平面内,否则就不在同一个平面内,其依据就是推论2.
不共线的三点,一条直线和这条直线外一点, 两条相交直线,两条平行直线,都能唯一确定一个平面.这些结论在后续研究直线和平面之间平行、 垂直关系时,也会经常用到.
1.判断下列命题是否正确,正确的在括号内画“√”,错误的画“×”.
(1)书桌面是平面. ( )
(2)平面α与平面β相交,它们有有限个公共点. ( )
(3)如果两个平面有三个不共线的公共点,那么这两个平面重合. ( )
(1)× 平面是无限延展的;
(2)× 由基本事实2可知一定有无限个公共点;
(3)√ 由基本事实1可知正确.
×
×
√
2.下列命题正确的是( )
(A)三点确定一个平面
(B)一条直线和一个点确定一个平面
(C)圆心和圆上两点可确定一个平面
(D)梯形可确定一个平面
A错误,因为三点可能共线,也可能不共线;
B错误,因为可能点在直线上,或不在直线上;
C错误,因为圆上两点可能是直径的端点,此时三点共线.
D
P
A
B
C
3.不共面的四点可以确定几个平面?请画出图形说明你的结论.
不共面的四点可以确定4个平面.
A
B
(1)
M
a
a
M
(2)
a
(3)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
