8.1.1 变量的相关关系-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册课件(14张PPT)
文档属性
| 名称 | 8.1.1 变量的相关关系-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册课件(14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 20:56:51 | ||
图片预览





文档简介
8.1 成对数据的统计相关性
1.会画出成对样本数据的散点图;
2.会通过散点图判断成对样本数据的相关性;
如果变量y是变量x的函数,那么由x就可以唯一确定y.
情景引入
然而,现实世界中还存在这样的情况:两个变量之间有关系,但密切程度又达不到函数关系的程度.
但身高并不是决定体重的唯一一因素,例如生活中的饮食习惯、体育锻炼、睡眠时间以及遗传因素等也是影响体重的重要因素.
我们知道,一个人的体重与他的身高有关系.一般而言, 个子高的人往往体重值较大,个子矮的人往往体重值较小.
像这样,两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系。
练习1
下列变量之间的关系是相关关系的是( )
A.正方体的表面积与体积
B.光照时间与果树的产量
C.匀速行驶车辆的行驶距离与时间
D.某运动会中某代表团的足球队的比赛成绩与乒乓球队的比赛成绩
答案:B
A、C是函数关系,D无相关关系
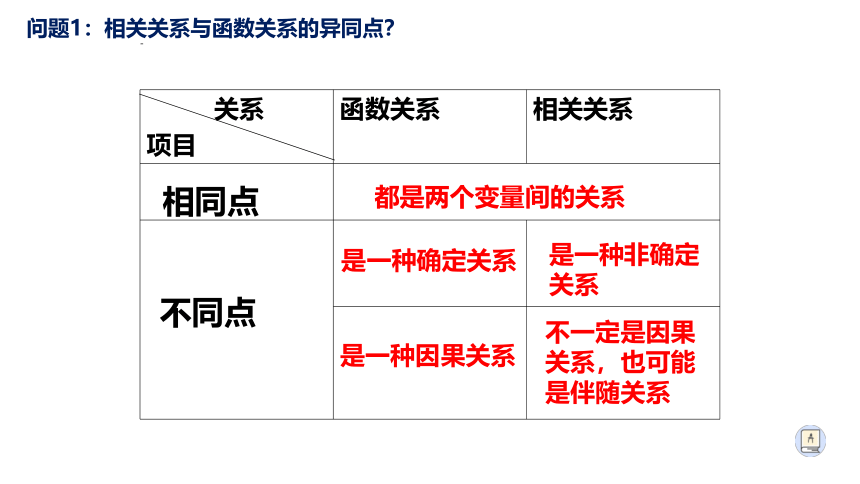
关系
项目
函数关系
相关关系
相同点
都是两个变量间的关系
不同点
是一种确定关系
是一种非确定关系
是一种因果关系
不一定是因果关系,也可能是伴随关系
问题1:相关关系与函数关系的异同点?
1.子女身高y与父亲身高x之间的关系。
2.商品销售收入y与广告支出x之间的关系。
3.空气污染指数y与汽车保有量x之间的关系.
问题2:
两个变量具有关系的事例:
4.粮食亩产量y与施肥量x之间的关系.
对两个变量之间的相关关系,我们往往会根据自己以往积累的经验作出推断。“经验之中有规律”,经验的确可以为我们的决策提供一定的依据,但仅凭经验推断又有不足。例如经验比较主观、经验不具有普适性等。
因此,在研究两个变量之间的相关系时,我们需要借助数据说话,即通过样本数据分析,从数据中提取信息,并构建适当的模型,再利用模型进行估计或推断.
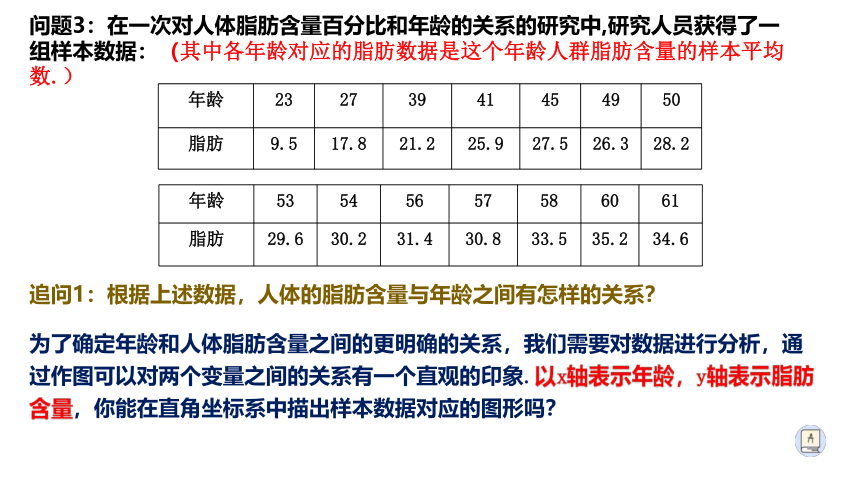
问题3:在一次对人体脂肪含量百分比和年龄的关系的研究中,研究人员获得了一组样本数据:(其中各年龄对应的脂肪数据是这个年龄人群脂肪含量的样本平均数.)
{5940675A-B579-460E-94D1-54222C63F5DA}年龄
23
27
39
41
45
49
50
脂肪
9.5
17.8
21.2
25.9
27.5
26.3
28.2
{5940675A-B579-460E-94D1-54222C63F5DA}年龄
53
54
56
57
58
60
61
脂肪
29.6
30.2
31.4
30.8
33.5
35.2
34.6
追问1:根据上述数据,人体的脂肪含量与年龄之间有怎样的关系?
为了确定年龄和人体脂肪含量之间的更明确的关系,我们需要对数据进行分析,通过作图可以对两个变量之间的关系有一个直观的印象.以x轴表示年龄,y轴表示脂肪含量,你能在直角坐标系中描出样本数据对应的图形吗?
年龄/岁
脂肪含量/%
用图形展示成对样本数据的变化特征,成对样本数据都可用直角坐标系中的点表示出来,由这些点组成了统计图.我们把这样的统计图叫做散点图.
可以发现,这些散点大致落在一条从左下角到右上角的直线附近,表明随年龄值的增加,相应的脂肪含量值呈现增高的趋势.这样,由成对样本数据的分布规律,我们可以推断脂肪含量变量和年龄变量之间存在着相关关系.
变量相关关系的分类(一)
如果从整体上看,
当一个变量的值增加时,另一个变量的相应值呈现减少的趋势,则称这两个变量负相关。
当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,我们就称这两个变量正相关。
散点图中的点散布在从左下角到右上角的区域
追问1:两个变量正相关、负相关时,成对样本数据的散点图有什么特点?
散点图中的点散布在从左上角到右下角的区域
变量相关关系的分类(一)
散点图是描述成对数据之间关系的一种直观方法.一般地, 如果两个变量的取值呈现正相关或负相关,而且散点落在一一条直线附近,我们就称这两个变量线性相关
1.线性相关
一般地,如果两个变量具有相关性,但不是线性相关,那么我们就称这两个变量非线性相关或曲线相关.
2.非线性相关
变量相关关系的分类(二)
例1:某公司的利润y(单位:千万元)与销售总额x(单位:千万元)之间有如下表对应数据:
(1)画出散点图;
(2)判断y与x是否具有线性相关关系。
{5940675A-B579-460E-94D1-54222C63F5DA}x
10
15
17
20
25
28
32
y
1
1.3
1.8
2
2.6
2.7
3.3
解:(1)散点图如右图所示:
(2)由图可知,所有数据点接近直线排列,因此,认为y与x有线性相关关系,且为正相关。
课堂小结
成对样本数据
散点图
变量相关关系
定性推断
1.会画出成对样本数据的散点图;
2.会通过散点图判断成对样本数据的相关性;
如果变量y是变量x的函数,那么由x就可以唯一确定y.
情景引入
然而,现实世界中还存在这样的情况:两个变量之间有关系,但密切程度又达不到函数关系的程度.
但身高并不是决定体重的唯一一因素,例如生活中的饮食习惯、体育锻炼、睡眠时间以及遗传因素等也是影响体重的重要因素.
我们知道,一个人的体重与他的身高有关系.一般而言, 个子高的人往往体重值较大,个子矮的人往往体重值较小.
像这样,两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系。
练习1
下列变量之间的关系是相关关系的是( )
A.正方体的表面积与体积
B.光照时间与果树的产量
C.匀速行驶车辆的行驶距离与时间
D.某运动会中某代表团的足球队的比赛成绩与乒乓球队的比赛成绩
答案:B
A、C是函数关系,D无相关关系
关系
项目
函数关系
相关关系
相同点
都是两个变量间的关系
不同点
是一种确定关系
是一种非确定关系
是一种因果关系
不一定是因果关系,也可能是伴随关系
问题1:相关关系与函数关系的异同点?
1.子女身高y与父亲身高x之间的关系。
2.商品销售收入y与广告支出x之间的关系。
3.空气污染指数y与汽车保有量x之间的关系.
问题2:
两个变量具有关系的事例:
4.粮食亩产量y与施肥量x之间的关系.
对两个变量之间的相关关系,我们往往会根据自己以往积累的经验作出推断。“经验之中有规律”,经验的确可以为我们的决策提供一定的依据,但仅凭经验推断又有不足。例如经验比较主观、经验不具有普适性等。
因此,在研究两个变量之间的相关系时,我们需要借助数据说话,即通过样本数据分析,从数据中提取信息,并构建适当的模型,再利用模型进行估计或推断.
问题3:在一次对人体脂肪含量百分比和年龄的关系的研究中,研究人员获得了一组样本数据:(其中各年龄对应的脂肪数据是这个年龄人群脂肪含量的样本平均数.)
{5940675A-B579-460E-94D1-54222C63F5DA}年龄
23
27
39
41
45
49
50
脂肪
9.5
17.8
21.2
25.9
27.5
26.3
28.2
{5940675A-B579-460E-94D1-54222C63F5DA}年龄
53
54
56
57
58
60
61
脂肪
29.6
30.2
31.4
30.8
33.5
35.2
34.6
追问1:根据上述数据,人体的脂肪含量与年龄之间有怎样的关系?
为了确定年龄和人体脂肪含量之间的更明确的关系,我们需要对数据进行分析,通过作图可以对两个变量之间的关系有一个直观的印象.以x轴表示年龄,y轴表示脂肪含量,你能在直角坐标系中描出样本数据对应的图形吗?
年龄/岁
脂肪含量/%
用图形展示成对样本数据的变化特征,成对样本数据都可用直角坐标系中的点表示出来,由这些点组成了统计图.我们把这样的统计图叫做散点图.
可以发现,这些散点大致落在一条从左下角到右上角的直线附近,表明随年龄值的增加,相应的脂肪含量值呈现增高的趋势.这样,由成对样本数据的分布规律,我们可以推断脂肪含量变量和年龄变量之间存在着相关关系.
变量相关关系的分类(一)
如果从整体上看,
当一个变量的值增加时,另一个变量的相应值呈现减少的趋势,则称这两个变量负相关。
当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,我们就称这两个变量正相关。
散点图中的点散布在从左下角到右上角的区域
追问1:两个变量正相关、负相关时,成对样本数据的散点图有什么特点?
散点图中的点散布在从左上角到右下角的区域
变量相关关系的分类(一)
散点图是描述成对数据之间关系的一种直观方法.一般地, 如果两个变量的取值呈现正相关或负相关,而且散点落在一一条直线附近,我们就称这两个变量线性相关
1.线性相关
一般地,如果两个变量具有相关性,但不是线性相关,那么我们就称这两个变量非线性相关或曲线相关.
2.非线性相关
变量相关关系的分类(二)
例1:某公司的利润y(单位:千万元)与销售总额x(单位:千万元)之间有如下表对应数据:
(1)画出散点图;
(2)判断y与x是否具有线性相关关系。
{5940675A-B579-460E-94D1-54222C63F5DA}x
10
15
17
20
25
28
32
y
1
1.3
1.8
2
2.6
2.7
3.3
解:(1)散点图如右图所示:
(2)由图可知,所有数据点接近直线排列,因此,认为y与x有线性相关关系,且为正相关。
课堂小结
成对样本数据
散点图
变量相关关系
定性推断
