5.2.《平行线》
图片预览



文档简介
(共26张PPT)
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
同位角相等,两直线平行。
1、同位角相等,两直线平行。
即∵∠1=∠2(已知)
∴a∥b(同位角相等,两直线平行)
回顾 & 思考
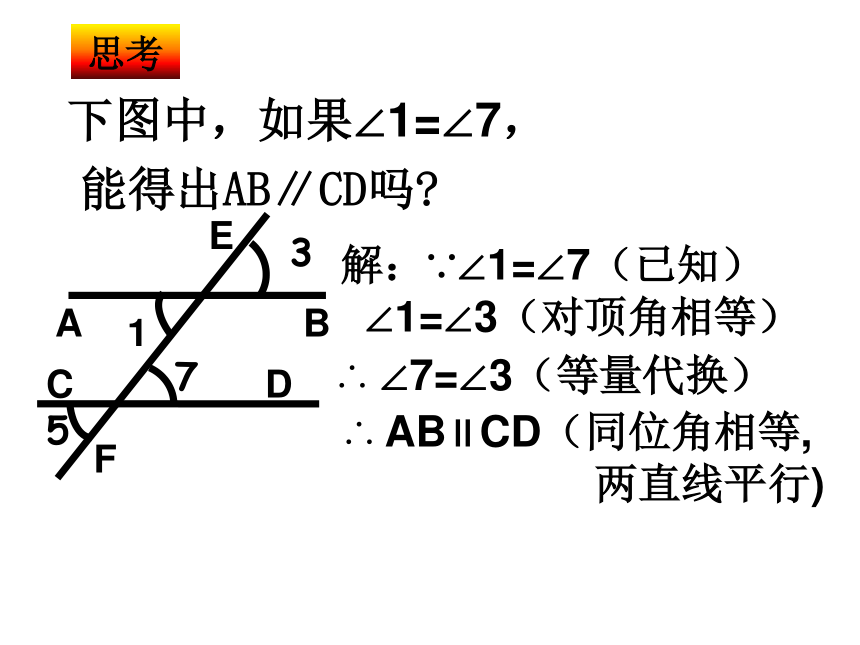
下图中,如果∠1=∠7,
能得出AB∥CD吗
思考
解:∵∠1=∠7(已知)
∠1=∠3(对顶角相等)
∴ ∠7=∠3(等量代换)
∴ AB∥CD(同位角相等,
两直线平行)
B
1
A
C
D
F
3
7
E
5
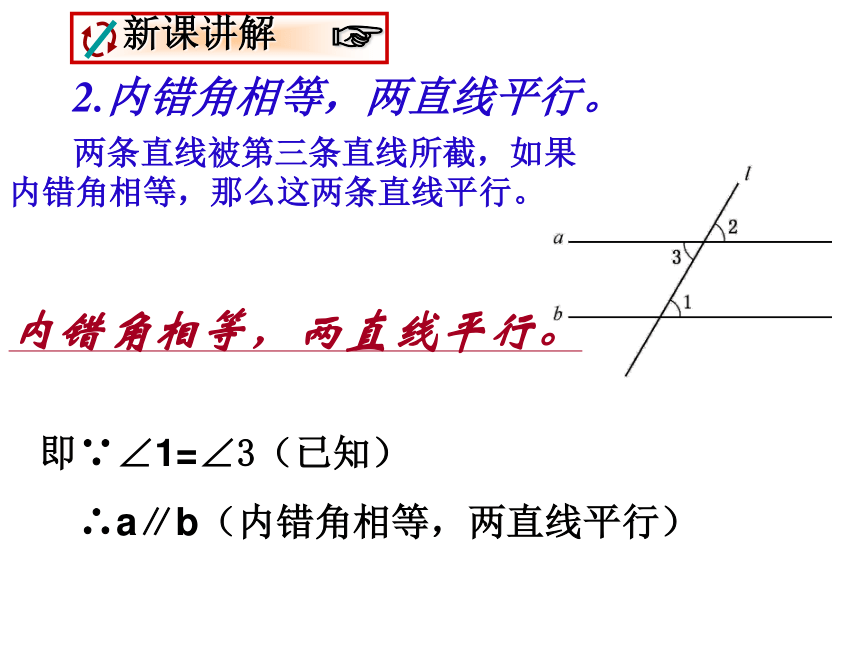
2.内错角相等,两直线平行。
如右图,如果∠1=∠3,因为
∠2=∠3(对顶角相等),所以就有
∠1=∠2,于是可得a∥b。
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
内错角相等,两直线平行。
即∵∠1=∠3(已知)
∴a∥b(内错角相等,两直线平行)
新课讲解
遇到一个新问题时,常常把它转化为
已知的(或已经解决的)问题来解决.
这一节中,我们是怎样利用“同位角相等,两直线平行”得到“内错角相等,两直线平行”的?你能利用“同位角相等,两直线平行”或“内错角相等
,两直线平行”得到“同旁内角互补,两直线平行”吗?
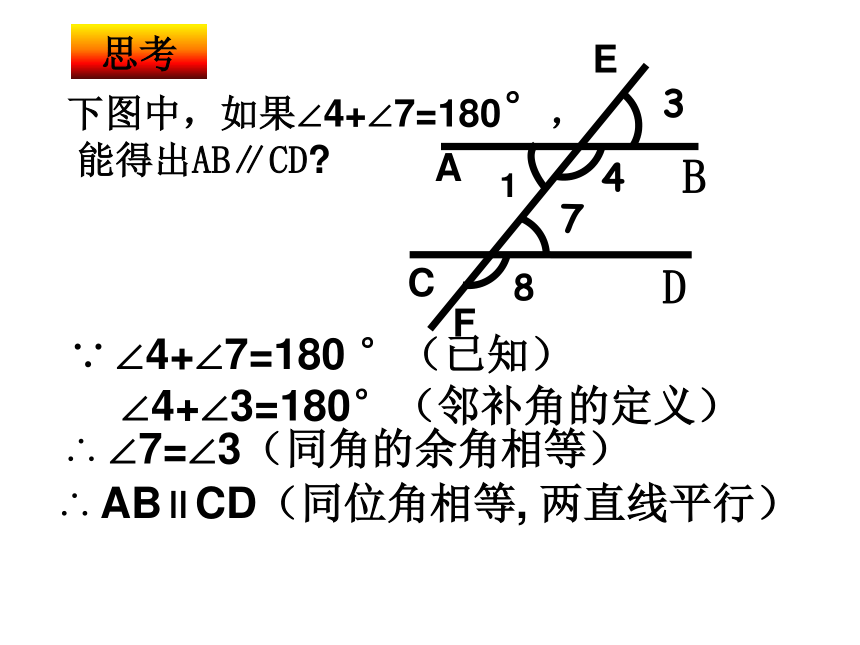
下图中,如果∠4+∠7=180°,
能得出AB∥CD
思考
∵ ∠4+∠7=180 °(已知)
∠4+∠3=180°(邻补角的定义)
∴ ∠7=∠3(同角的余角相等)
∴ AB∥CD(同位角相等, 两直线平行)
1
A
C
3
4
7
8
D
B
E
F
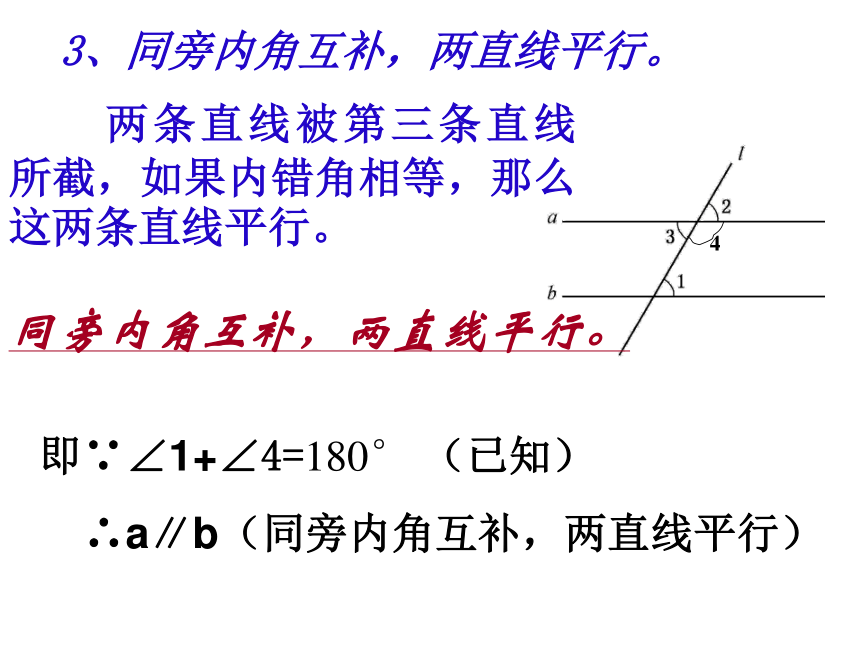
3、同旁内角互补,两直线平行。
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
4
同旁内角互补,两直线平行。
即∵∠1+∠4=180° (已知)
∴a∥b(同旁内角互补,两直线平行)
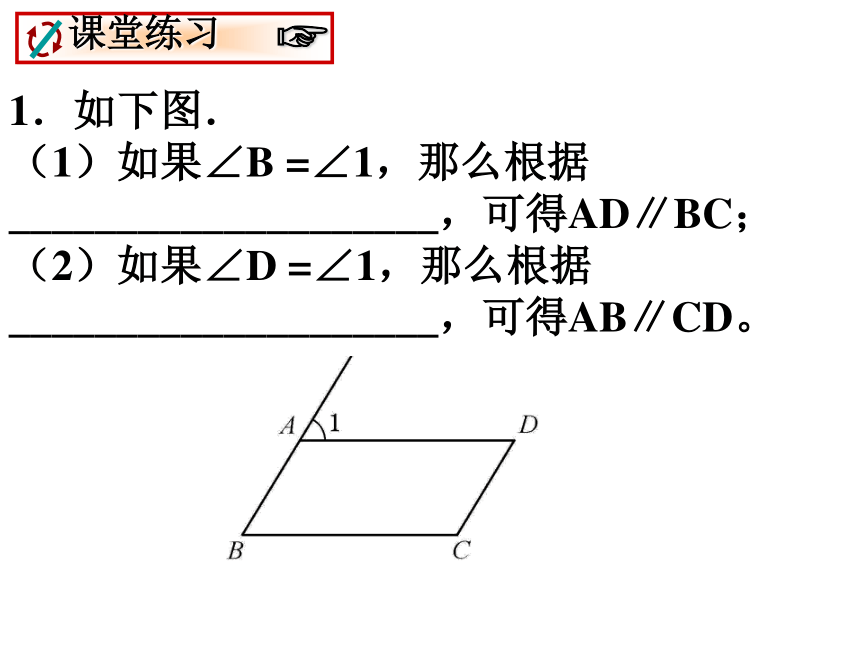
1.如下图.
(1)如果∠B =∠1,那么根据____________________,可得AD∥BC;
(2)如果∠D =∠1,那么根据____________________,可得AB∥CD。
(第1题)
课堂练习
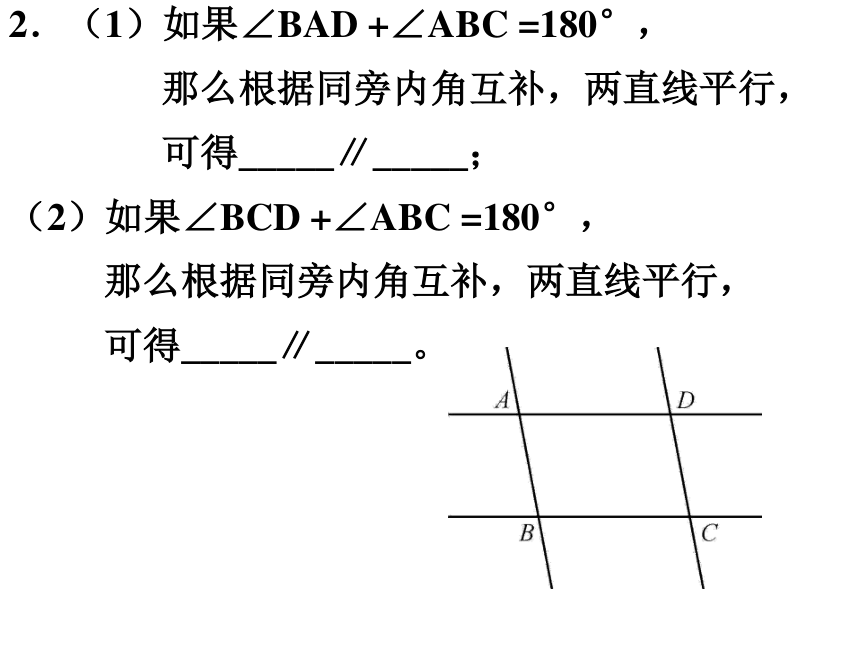
2.(1)如果∠BAD +∠ABC =180°,
那么根据同旁内角互补,两直线平行,
可得_____∥_____;
(2)如果∠BCD +∠ABC =180°,
那么根据同旁内角互补,两直线平行,
可得_____∥_____。
(第2题)
4.如图:在四边形ABCD中,∠1=40°,∠2=40°,AD与BC平行吗?为什么?
解:∵ ∠1=40°,∠2=40°(已知)
∴∠1=∠2
∴AD∥BC(内错角相等,两直线平行)
回顾与思考
例题讲解
例2 如图,已知∠AEC=∠C+∠A,判断AB与∥CD是否平行?并说明理由.
回顾与思考
分析:延长CE,交AB于点F,则直线CD,AB被直线CF所截。这样,我们可以通过判断内错角∠C和∠AFC是否相等,来判定AB与CD是否平行。
例2 如图,已知∠AEC=∠C+∠A,判断AB与∥CD是否平行?并说明理由.
回顾与思考
例2 如图,已知∠AEC=∠C+∠A,判断AB与∥CD是否平行?并说明理由.
1.如图,
(1)从∠1=∠2,可以推出 ∥ ,
理由是
(2)从∠2=∠ ,可以推出c∥d ,
理由是
(3)如果∠4=75°,∠3=75 °,
可以推出 ∥
(4) 从∠4=75°,∠5= °,
可以推出a∥b.
考考你
d
b
a
内错角相等,两直线平行
同位角相等,两直线平行.
3
3
a
b
1
2
5
4
c
d
c
105
2.如图,你有可以添加哪些条件使得
AB∥CD?
考考你
F
E
2
B
1
A
C
D
3
4
5
6
7
8
有一块木板,怎样才能知道它上下边缘是否平行?
考考你
有一块木板,怎样才能知道它上下边缘是否平行?
1
2
考考你
有一块木板,怎样才能知道它上下边缘是否平行?
1
2
考考你
1
2
有一块木板,怎样才能知道它上下边缘是否平行?
考考你
1
2
能力挑战:
(A)∠2=∠3 (B)∠1=∠4
(C)∠1=∠2 (D)∠1=∠3
D
1、如图,不能判定 的是 ( )
能力挑战:
2、如图,∠1=∠2,则下列结论正确的是( )
(A)AD//BC (B)AB//CD
(C)AD//EF (D)EF//BC
C
能力挑战:
3、如图,哪些直线平行,哪些直线不平行?
与 平行, 与 不平行
如图,已知直线 ,被直线AB所截,AC⊥ 于点C。若∠1=50°,∠2=40°,则 与 平行吗?请说明理由。
能力挑战:
通过这节课的学习,
你有哪些收获
议一议
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5. 平行线的定义.
判定两条直线是否平行的方法有:
课后作业
习题
1,2,4,6
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
同位角相等,两直线平行。
1、同位角相等,两直线平行。
即∵∠1=∠2(已知)
∴a∥b(同位角相等,两直线平行)
回顾 & 思考
下图中,如果∠1=∠7,
能得出AB∥CD吗
思考
解:∵∠1=∠7(已知)
∠1=∠3(对顶角相等)
∴ ∠7=∠3(等量代换)
∴ AB∥CD(同位角相等,
两直线平行)
B
1
A
C
D
F
3
7
E
5
2.内错角相等,两直线平行。
如右图,如果∠1=∠3,因为
∠2=∠3(对顶角相等),所以就有
∠1=∠2,于是可得a∥b。
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
内错角相等,两直线平行。
即∵∠1=∠3(已知)
∴a∥b(内错角相等,两直线平行)
新课讲解
遇到一个新问题时,常常把它转化为
已知的(或已经解决的)问题来解决.
这一节中,我们是怎样利用“同位角相等,两直线平行”得到“内错角相等,两直线平行”的?你能利用“同位角相等,两直线平行”或“内错角相等
,两直线平行”得到“同旁内角互补,两直线平行”吗?
下图中,如果∠4+∠7=180°,
能得出AB∥CD
思考
∵ ∠4+∠7=180 °(已知)
∠4+∠3=180°(邻补角的定义)
∴ ∠7=∠3(同角的余角相等)
∴ AB∥CD(同位角相等, 两直线平行)
1
A
C
3
4
7
8
D
B
E
F
3、同旁内角互补,两直线平行。
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
4
同旁内角互补,两直线平行。
即∵∠1+∠4=180° (已知)
∴a∥b(同旁内角互补,两直线平行)
1.如下图.
(1)如果∠B =∠1,那么根据____________________,可得AD∥BC;
(2)如果∠D =∠1,那么根据____________________,可得AB∥CD。
(第1题)
课堂练习
2.(1)如果∠BAD +∠ABC =180°,
那么根据同旁内角互补,两直线平行,
可得_____∥_____;
(2)如果∠BCD +∠ABC =180°,
那么根据同旁内角互补,两直线平行,
可得_____∥_____。
(第2题)
4.如图:在四边形ABCD中,∠1=40°,∠2=40°,AD与BC平行吗?为什么?
解:∵ ∠1=40°,∠2=40°(已知)
∴∠1=∠2
∴AD∥BC(内错角相等,两直线平行)
回顾与思考
例题讲解
例2 如图,已知∠AEC=∠C+∠A,判断AB与∥CD是否平行?并说明理由.
回顾与思考
分析:延长CE,交AB于点F,则直线CD,AB被直线CF所截。这样,我们可以通过判断内错角∠C和∠AFC是否相等,来判定AB与CD是否平行。
例2 如图,已知∠AEC=∠C+∠A,判断AB与∥CD是否平行?并说明理由.
回顾与思考
例2 如图,已知∠AEC=∠C+∠A,判断AB与∥CD是否平行?并说明理由.
1.如图,
(1)从∠1=∠2,可以推出 ∥ ,
理由是
(2)从∠2=∠ ,可以推出c∥d ,
理由是
(3)如果∠4=75°,∠3=75 °,
可以推出 ∥
(4) 从∠4=75°,∠5= °,
可以推出a∥b.
考考你
d
b
a
内错角相等,两直线平行
同位角相等,两直线平行.
3
3
a
b
1
2
5
4
c
d
c
105
2.如图,你有可以添加哪些条件使得
AB∥CD?
考考你
F
E
2
B
1
A
C
D
3
4
5
6
7
8
有一块木板,怎样才能知道它上下边缘是否平行?
考考你
有一块木板,怎样才能知道它上下边缘是否平行?
1
2
考考你
有一块木板,怎样才能知道它上下边缘是否平行?
1
2
考考你
1
2
有一块木板,怎样才能知道它上下边缘是否平行?
考考你
1
2
能力挑战:
(A)∠2=∠3 (B)∠1=∠4
(C)∠1=∠2 (D)∠1=∠3
D
1、如图,不能判定 的是 ( )
能力挑战:
2、如图,∠1=∠2,则下列结论正确的是( )
(A)AD//BC (B)AB//CD
(C)AD//EF (D)EF//BC
C
能力挑战:
3、如图,哪些直线平行,哪些直线不平行?
与 平行, 与 不平行
如图,已知直线 ,被直线AB所截,AC⊥ 于点C。若∠1=50°,∠2=40°,则 与 平行吗?请说明理由。
能力挑战:
通过这节课的学习,
你有哪些收获
议一议
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5. 平行线的定义.
判定两条直线是否平行的方法有:
课后作业
习题
1,2,4,6
