5.2.1《平行线》
图片预览




文档简介
(共17张PPT)
2
《数学》(人教版.七年级 下册)
回顾与思考
回顾 & 思考
在同一平面内
相交
平行
(填空完成下列) 二直线的位置关系:
的两直线叫做平行线.
同一平面内,不相交
同一平面内
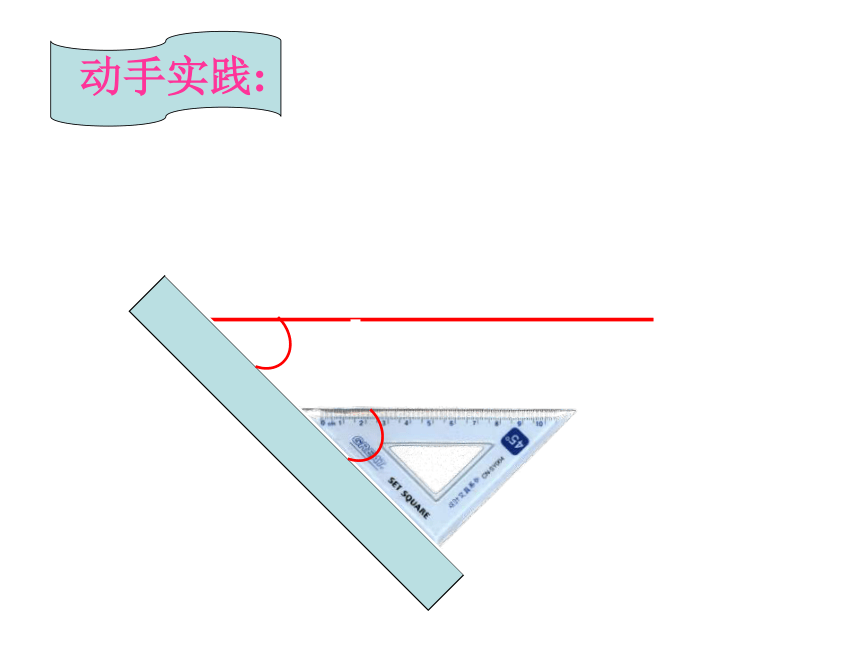
还记得如何用三角板和直尺画平行线吗?
一放、二靠、三推、四画。
1
2
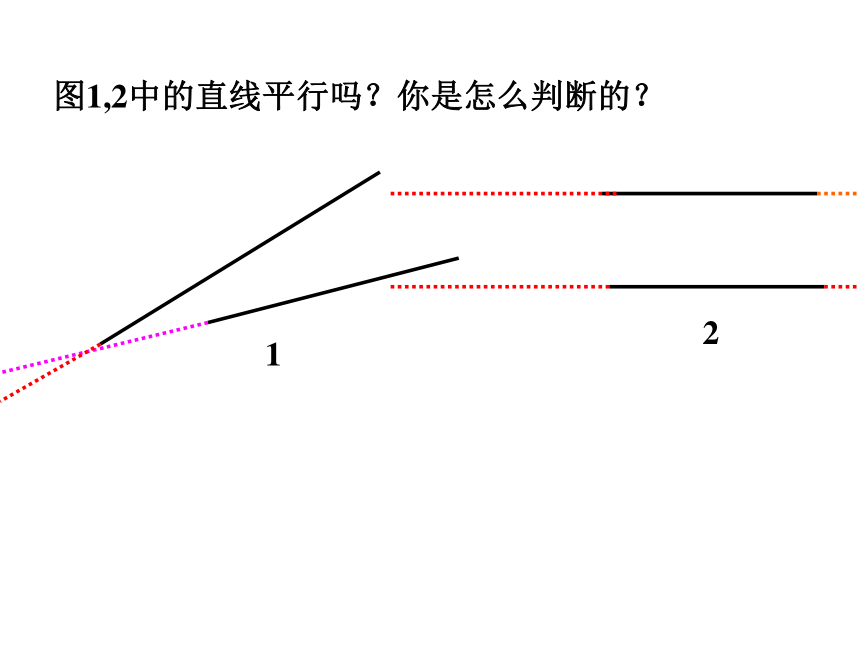
图1,2中的直线平行吗?你是怎么判断的?
如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角多少度时,才能使木条a与木条b平行?
怎样使得两根木条保持平行呢?
答:当木条a与墙壁边缘成90度时。
过直线AB外一点P作直线AB的平行线,看看你能作出吗?能作出几条?
·
A
B
P
动手实践:
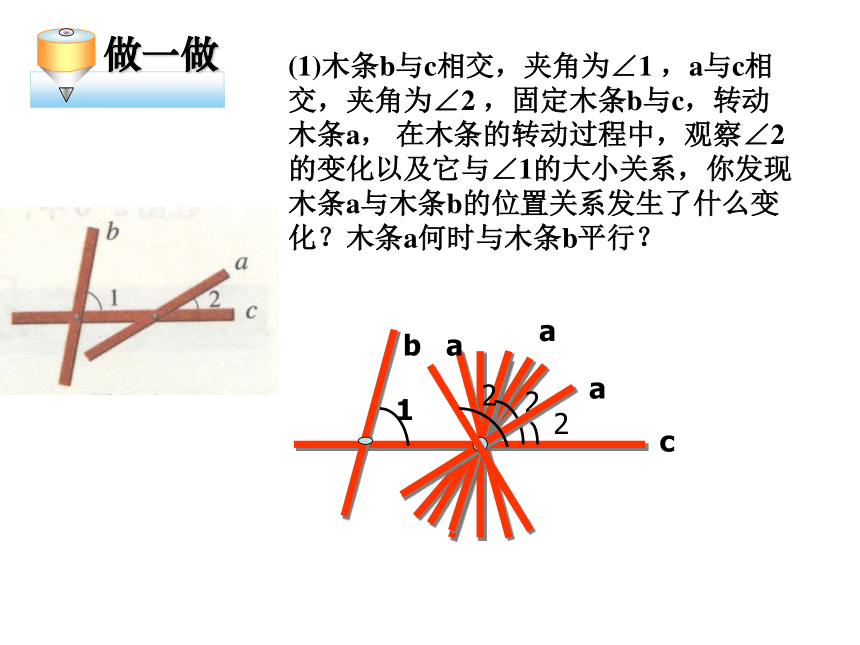
(1)木条b与c相交,夹角为∠1 ,a与c相交,夹角为∠2 ,固定木条b与c,转动木条a, 在木条的转动过程中,观察∠2的变化以及它与∠1的大小关系,你发现木条a与木条b的位置关系发生了什么变化?木条a何时与木条b平行?
1
b
c
a
2
2
a
2
a
做一做
当∠2 < ∠1时
当∠2=∠1时
当∠2> ∠1时
①直线a和b不平行
②直线a∥b
③直线a和b不平行
想一想
判断两条直线平行的一种方法:
由此可得:
平行判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
当∠1>∠2时
①直线a和b ,
当∠1=∠2时
②直线a b;
当∠1<∠2时
③直线a和b 。
回到两直线平行的判断上来
不平行
∥
不平行
1
2
同位角相等,两直线平行。
两直线 平行的判定
∠1、∠2是 角。
同位
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
∵∠1 = ∠2 (已知)
∴ a ∥ b (同位角相等,两直线平行).
符号语言
①找出同位角;
②说明这两个同位角相等;
③得出“平行”的结论。
用判定定理1应该注意:
例题解析
例1:如图,∠ 1= ∠C ,∠ 2= ∠C ,请找出图中互相平行的直线,并说明理由.
A
B
C
D
2
1
解:AB∥CD,AC∥BD,理由如下:
∵∠1 = ∠C (已知)
∴ AB ∥ CD (同位角相等,两直线平行).
同理可得:AC∥BD
例2、如图,∠1 = ∠2 = 55°, ∠3等于
多少度?直线AB、CD平行吗?说明你的
理由。
第2题图
3
1
2
A
B
F
C
D
E
∵ ∠2 = 55°
∴ ∠3 = ∠2 =55°
∴ ∠3 =∠1= 55°
∴ AB∥CD.
随堂练习
( )
对顶角相等
解: AB∥CD. 理由如下:
(已知)
(等量代换)
(同位角相等,两直线平行)
∵ ∠1= 55°
(已知)
例2、如图,∠1 = ∠2 = 55°, ∠3等于
多少度?直线AB、CD平行吗?说明你的
理由。
第2题图
3
1
2
A
B
F
C
D
E
随堂练习
解: ①∵∠3与∠2互为对顶角
∴∠3=∠2=55°
②AB∥CD. 理由如下:
∵∠1=∠2(已知)
∠3=∠2(对顶角相等)
∴∠1=∠3(等量代换)
∴AB∥CD(同位角相等两直线平行)
1、找出下面点阵图中互相平行的线段,并说明理由. (点阵中相邻的四个点构成正方形)
① AB∥CD.
② EF∥GH.
∵ ∠AMP=∠CPF=45°
∴ AB∥CD.
∵ ∠AMP=∠ANQ=45°,
∴ EF∥GH.
E
G
B
D
F
H
请看下面的推理是否正确
∵ ∠AMP=∠CQH
∴ EF∥GH。
A
C
M
N
P
Q
判断二直线平行——
一定要借助第三线;
两角必须是同位角。
随堂练习
牛刀小试
3.如图, ∠1=70°,在给出的下列条件中,能判定AB ∥ CD的条件的是( )
(A)∠2= 70°(B) ∠3= 110°
( C)∠4= 70°(D )∠5= 70°
D
第3题图
4.如图,∠1=65°,∠B=65°,
可以判断__ ∥____,理由是_________________.
3
E
D
C
B
A
1
D
C
B
A
第4题图 第5题图
5.∠3=30°,当∠ABE=______时,就能使 BE∥CD?
AD BC
同位角相等,两直线平行
150°
思维拓展
在如图所示的图中,甲从A处沿东偏南55°方向行走,乙从B处沿东偏南35°方向行走,(1)他们所行道路可能相交吗?
(2)当乙从B处沿什么方向行走,他们所行道路不相交?请说明其中的理由.
乙
甲
35°
55°
1
2
B
A
每得出一个两直线平行的结论,
都要依序完成下列三个过程:
本节课你的收获是什么?
“同位角相等,两直线平行”
①找出同位角;
②说明这两个同位角相等;
③得出“平行”的结论。
2
《数学》(人教版.七年级 下册)
回顾与思考
回顾 & 思考
在同一平面内
相交
平行
(填空完成下列) 二直线的位置关系:
的两直线叫做平行线.
同一平面内,不相交
同一平面内
还记得如何用三角板和直尺画平行线吗?
一放、二靠、三推、四画。
1
2
图1,2中的直线平行吗?你是怎么判断的?
如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角多少度时,才能使木条a与木条b平行?
怎样使得两根木条保持平行呢?
答:当木条a与墙壁边缘成90度时。
过直线AB外一点P作直线AB的平行线,看看你能作出吗?能作出几条?
·
A
B
P
动手实践:
(1)木条b与c相交,夹角为∠1 ,a与c相交,夹角为∠2 ,固定木条b与c,转动木条a, 在木条的转动过程中,观察∠2的变化以及它与∠1的大小关系,你发现木条a与木条b的位置关系发生了什么变化?木条a何时与木条b平行?
1
b
c
a
2
2
a
2
a
做一做
当∠2 < ∠1时
当∠2=∠1时
当∠2> ∠1时
①直线a和b不平行
②直线a∥b
③直线a和b不平行
想一想
判断两条直线平行的一种方法:
由此可得:
平行判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
当∠1>∠2时
①直线a和b ,
当∠1=∠2时
②直线a b;
当∠1<∠2时
③直线a和b 。
回到两直线平行的判断上来
不平行
∥
不平行
1
2
同位角相等,两直线平行。
两直线 平行的判定
∠1、∠2是 角。
同位
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
∵∠1 = ∠2 (已知)
∴ a ∥ b (同位角相等,两直线平行).
符号语言
①找出同位角;
②说明这两个同位角相等;
③得出“平行”的结论。
用判定定理1应该注意:
例题解析
例1:如图,∠ 1= ∠C ,∠ 2= ∠C ,请找出图中互相平行的直线,并说明理由.
A
B
C
D
2
1
解:AB∥CD,AC∥BD,理由如下:
∵∠1 = ∠C (已知)
∴ AB ∥ CD (同位角相等,两直线平行).
同理可得:AC∥BD
例2、如图,∠1 = ∠2 = 55°, ∠3等于
多少度?直线AB、CD平行吗?说明你的
理由。
第2题图
3
1
2
A
B
F
C
D
E
∵ ∠2 = 55°
∴ ∠3 = ∠2 =55°
∴ ∠3 =∠1= 55°
∴ AB∥CD.
随堂练习
( )
对顶角相等
解: AB∥CD. 理由如下:
(已知)
(等量代换)
(同位角相等,两直线平行)
∵ ∠1= 55°
(已知)
例2、如图,∠1 = ∠2 = 55°, ∠3等于
多少度?直线AB、CD平行吗?说明你的
理由。
第2题图
3
1
2
A
B
F
C
D
E
随堂练习
解: ①∵∠3与∠2互为对顶角
∴∠3=∠2=55°
②AB∥CD. 理由如下:
∵∠1=∠2(已知)
∠3=∠2(对顶角相等)
∴∠1=∠3(等量代换)
∴AB∥CD(同位角相等两直线平行)
1、找出下面点阵图中互相平行的线段,并说明理由. (点阵中相邻的四个点构成正方形)
① AB∥CD.
② EF∥GH.
∵ ∠AMP=∠CPF=45°
∴ AB∥CD.
∵ ∠AMP=∠ANQ=45°,
∴ EF∥GH.
E
G
B
D
F
H
请看下面的推理是否正确
∵ ∠AMP=∠CQH
∴ EF∥GH。
A
C
M
N
P
Q
判断二直线平行——
一定要借助第三线;
两角必须是同位角。
随堂练习
牛刀小试
3.如图, ∠1=70°,在给出的下列条件中,能判定AB ∥ CD的条件的是( )
(A)∠2= 70°(B) ∠3= 110°
( C)∠4= 70°(D )∠5= 70°
D
第3题图
4.如图,∠1=65°,∠B=65°,
可以判断__ ∥____,理由是_________________.
3
E
D
C
B
A
1
D
C
B
A
第4题图 第5题图
5.∠3=30°,当∠ABE=______时,就能使 BE∥CD?
AD BC
同位角相等,两直线平行
150°
思维拓展
在如图所示的图中,甲从A处沿东偏南55°方向行走,乙从B处沿东偏南35°方向行走,(1)他们所行道路可能相交吗?
(2)当乙从B处沿什么方向行走,他们所行道路不相交?请说明其中的理由.
乙
甲
35°
55°
1
2
B
A
每得出一个两直线平行的结论,
都要依序完成下列三个过程:
本节课你的收获是什么?
“同位角相等,两直线平行”
①找出同位角;
②说明这两个同位角相等;
③得出“平行”的结论。
