2.2.2对数函数的图像与性质 课件-人教版高中数学必修一(27张PPT)
文档属性
| 名称 | 2.2.2对数函数的图像与性质 课件-人教版高中数学必修一(27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 21:08:57 | ||
图片预览





文档简介
对数函数及其性质
2. 2. 2
生物体死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”。根据此规律,人们获得了生物体内碳14含量P与死亡年数t之间的关系,
新课讲解:
(一)对数函数的定义:
函数
叫做对数函数;
其中x是自变量,函数的定义域是(0,+∞).
注意 1、对数函数对底数的限制:
且
判断是不是对数函数
(1)
(×)
(×)
(×)
(×)
(×)
哈哈 ,我们都不是对数函数
我们是对数型函数
请认清我们哈
学习函数的一般模式(方法):
解析式(定义)
图像
性质
应用
数形结合
①定义域
②值域
③单调性
⑤奇偶性
④最值
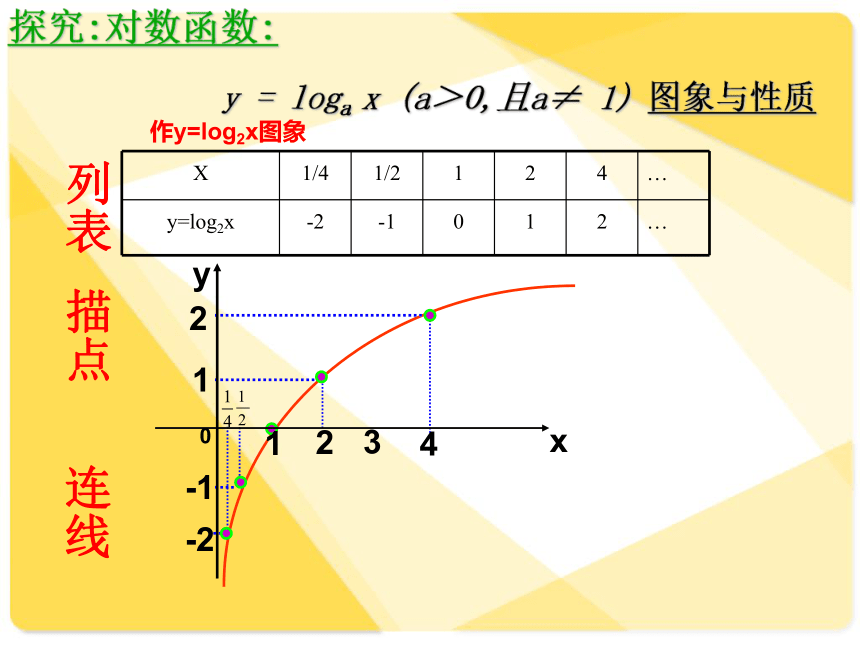
X
1/4
1/2
1
2
4
…
y=log2x
-2
-1
0
1
2
…
列表
描点
作y=log2x图象
连线
2
1
-1
-2
1
2
4
0
y
x
3
探究:对数函数:
y = loga x (a>0,且a≠ 1) 图象与性质
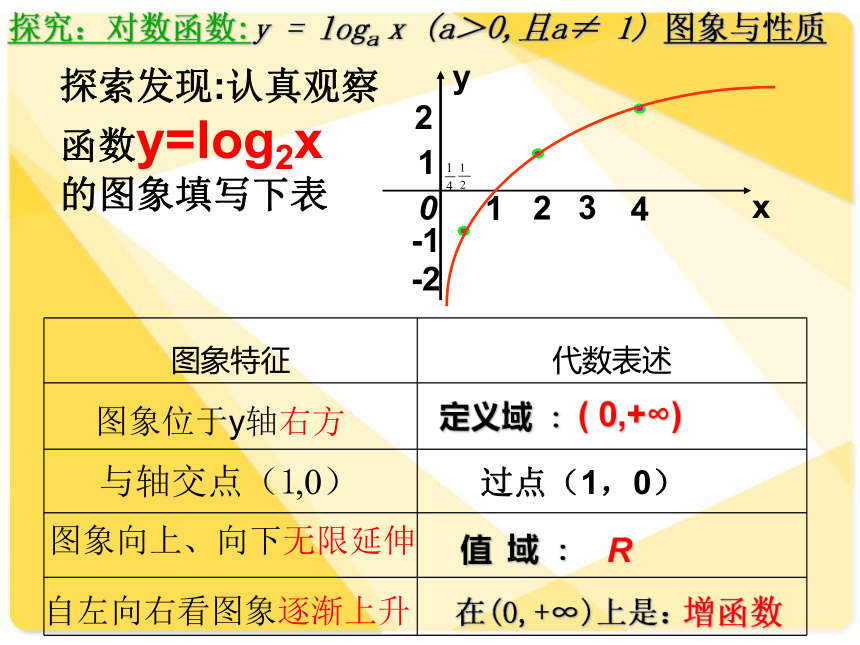
图象特征
代数表述
定义域 :
( 0,+∞)
值 域 :
R
增函数
在(0,+∞)上是:
探索发现:认真观察函数y=log2x
的图象填写下表
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐上升
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
2
1
-1
-2
1
2
4
0
y
x
3
过点(1,0)
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
x
1/4
1/2
1
2
4
2 1 0 -1 -2
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
…
…
…
…
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
发现:认真观察函数
的图象填写下表
2
1
-1
-2
1
2
4
0
y
x
3
图象特征
代数表述
定义域 :
( 0,+∞)
值 域 :
R
减函数
在(0,+∞)上是:
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐下降
过点(1,0)
对数函数 的图象。
猜猜:
2
1
-1
-2
1
2
4
0
y
x
3
对数函数在第一象限越靠近y轴底数越小
1
y
x
o
0< c< d < 1< a < b
C d 1 a b
由下面对数函数的图像判断底数a,b,c,d的大小
对数函数在第一象限越靠近y轴底数越小
2.对数函数的图象和性质
a>1
图
象
性
质
定义域
值域
特殊点
单调性
奇偶性
最值
过点(1,0)
在(0,+?)上是增函数
在(0,+?)上是减函数
当x>1时,y>0;
当0(0,+?)
R
非奇非偶函数
非奇非偶函数
0过点(1,0)
无最值
无最值
y
X
O
x =1
(1,0)
y
X
O
x =1
(1,0)
(0,+?)
R
当x>1时,y<0;
当00.
我很重要
练习1:求下列函数的定义域
① ②
例2 比较下列各组数中两个值的大小:
⑴ log 23.4 , log 28.5
⑵ log 0.31.8 , log 0.32.7
⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )
解:⑴∵对数函数y = log 2x
在(0,+∞)上是增函数
∴ log 23.4<log 28.5
⑵∵对数函数 y = log 0.3 x,
在(0,+∞)上是减函数,
∴log 0.31.8>log 0.32.7
且 3.4<8.5
且1.8<2.7
(3)当a>1时,函数y=log ax在(0,+∞)上是增函数,于是
log a5.1<log a5.9
log a5.1>log a5.9
当0<a<1时,函数y=log ax在(0,+∞)上是减函数,于是
两个同底对数比较大小,构造一个对数函数,然后用单调性比较
你能口答吗?
变一变还能口答吗?
<
,则m___n;
则m___n.
>
<
>
① 因为log35 > log33 =1
log53 < log55 =1
得:log 35 > log 53
例.比较大小
(1) log35 log53
② 因为log 32 > 0
log 20.8 < 0
得:log 32 > log 20.8
当底数不相同,真数也不相同时,
方法
10
>
>
常需引入中间值0或1(各种变形式).
解:
(2) log32 log20.8
例 比较大小:
1) log64 log74
解:
方法
当底数不相同,真数相同时,写成倒数形式比较大小
11
<
例 比较大小:
1) log53 log43
解:
利用对数函数图象
得到 log53 < log43
方法
当底数不相同,真数相同时,利用图象判断大小.
11
<
y1=log4x
y2=log5x
x
o
y
1
3
小结:
1.正确理解对数函数的定义;
2.掌握对数函数的图象和性质;
3.能利用对数函数的性质解决有关问题.
作业: 优化设计相应习题
2. 2. 2
生物体死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”。根据此规律,人们获得了生物体内碳14含量P与死亡年数t之间的关系,
新课讲解:
(一)对数函数的定义:
函数
叫做对数函数;
其中x是自变量,函数的定义域是(0,+∞).
注意 1、对数函数对底数的限制:
且
判断是不是对数函数
(1)
(×)
(×)
(×)
(×)
(×)
哈哈 ,我们都不是对数函数
我们是对数型函数
请认清我们哈
学习函数的一般模式(方法):
解析式(定义)
图像
性质
应用
数形结合
①定义域
②值域
③单调性
⑤奇偶性
④最值
X
1/4
1/2
1
2
4
…
y=log2x
-2
-1
0
1
2
…
列表
描点
作y=log2x图象
连线
2
1
-1
-2
1
2
4
0
y
x
3
探究:对数函数:
y = loga x (a>0,且a≠ 1) 图象与性质
图象特征
代数表述
定义域 :
( 0,+∞)
值 域 :
R
增函数
在(0,+∞)上是:
探索发现:认真观察函数y=log2x
的图象填写下表
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐上升
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
2
1
-1
-2
1
2
4
0
y
x
3
过点(1,0)
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
x
1/4
1/2
1
2
4
2 1 0 -1 -2
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
…
…
…
…
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
发现:认真观察函数
的图象填写下表
2
1
-1
-2
1
2
4
0
y
x
3
图象特征
代数表述
定义域 :
( 0,+∞)
值 域 :
R
减函数
在(0,+∞)上是:
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐下降
过点(1,0)
对数函数 的图象。
猜猜:
2
1
-1
-2
1
2
4
0
y
x
3
对数函数在第一象限越靠近y轴底数越小
1
y
x
o
0< c< d < 1< a < b
C d 1 a b
由下面对数函数的图像判断底数a,b,c,d的大小
对数函数在第一象限越靠近y轴底数越小
2.对数函数的图象和性质
a>1
图
象
性
质
定义域
值域
特殊点
单调性
奇偶性
最值
过点(1,0)
在(0,+?)上是增函数
在(0,+?)上是减函数
当x>1时,y>0;
当0
R
非奇非偶函数
非奇非偶函数
0
无最值
无最值
y
X
O
x =1
(1,0)
y
X
O
x =1
(1,0)
(0,+?)
R
当x>1时,y<0;
当0
我很重要
练习1:求下列函数的定义域
① ②
例2 比较下列各组数中两个值的大小:
⑴ log 23.4 , log 28.5
⑵ log 0.31.8 , log 0.32.7
⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )
解:⑴∵对数函数y = log 2x
在(0,+∞)上是增函数
∴ log 23.4<log 28.5
⑵∵对数函数 y = log 0.3 x,
在(0,+∞)上是减函数,
∴log 0.31.8>log 0.32.7
且 3.4<8.5
且1.8<2.7
(3)当a>1时,函数y=log ax在(0,+∞)上是增函数,于是
log a5.1<log a5.9
log a5.1>log a5.9
当0<a<1时,函数y=log ax在(0,+∞)上是减函数,于是
两个同底对数比较大小,构造一个对数函数,然后用单调性比较
你能口答吗?
变一变还能口答吗?
<
,则m___n;
则m___n.
>
<
>
① 因为log35 > log33 =1
log53 < log55 =1
得:log 35 > log 53
例.比较大小
(1) log35 log53
② 因为log 32 > 0
log 20.8 < 0
得:log 32 > log 20.8
当底数不相同,真数也不相同时,
方法
10
>
>
常需引入中间值0或1(各种变形式).
解:
(2) log32 log20.8
例 比较大小:
1) log64 log74
解:
方法
当底数不相同,真数相同时,写成倒数形式比较大小
11
<
例 比较大小:
1) log53 log43
解:
利用对数函数图象
得到 log53 < log43
方法
当底数不相同,真数相同时,利用图象判断大小.
11
<
y1=log4x
y2=log5x
x
o
y
1
3
小结:
1.正确理解对数函数的定义;
2.掌握对数函数的图象和性质;
3.能利用对数函数的性质解决有关问题.
作业: 优化设计相应习题
