人教A版必修2第二章2.3.1 直线与平面垂直的判定 课件(共29张PPT)
文档属性
| 名称 | 人教A版必修2第二章2.3.1 直线与平面垂直的判定 课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 21:27:00 | ||
图片预览





文档简介
2.3.1直线与平面垂直的判定
生活中有很多直线与平面垂直的实例,你能举出几个吗?
实例引入
旗杆与底面垂直
(一)平面垂直定义的建构
桥柱与水面的位置关系,给人以直线与平面垂直的形象.
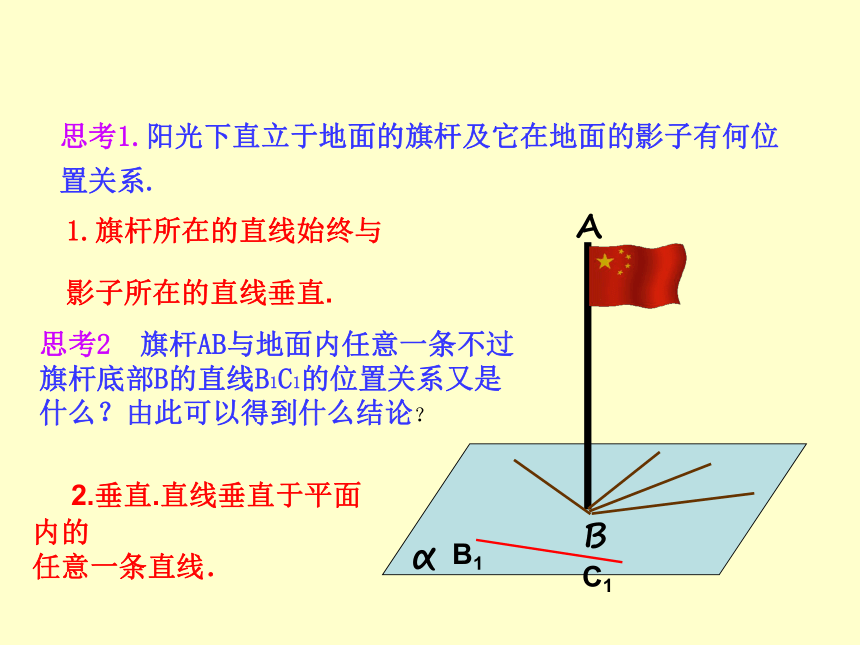
思考1.阳光下直立于地面的旗杆及它在地面的影子有何位置关系.
A
B
α
1.旗杆所在的直线始终与
影子所在的直线垂直.
C1
B1
思考2 旗杆AB与地面内任意一条不过旗杆底部B的直线B1C1的位置关系又是什么?由此可以得到什么结论?
2.垂直.直线垂直于平面内的
任意一条直线.
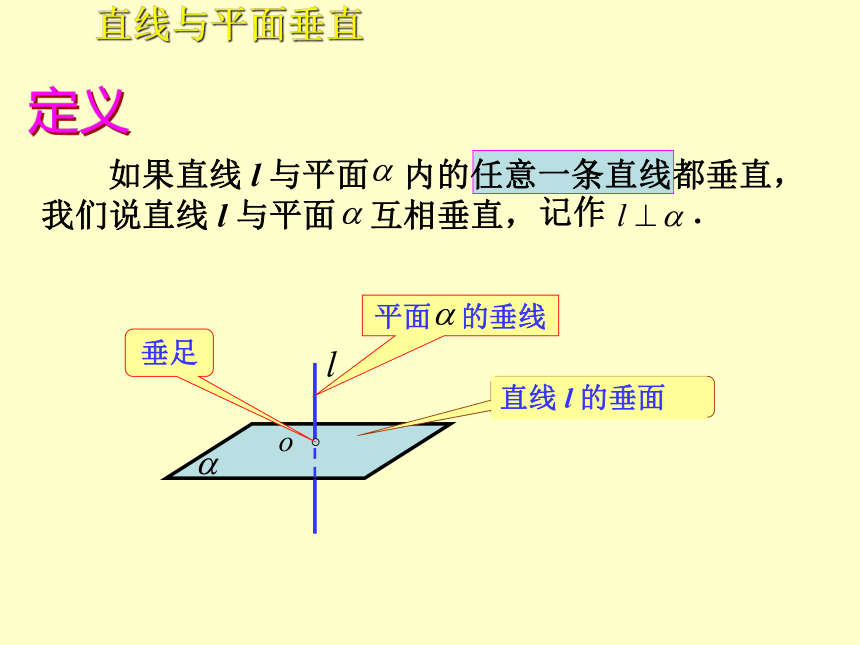
如果直线 l 与平面 内的任意一条直线都垂直,我们说直线 l 与平面 互相垂直,
记作 .
平面 的垂线
直线 l 的垂面
垂足
直线与平面垂直
?
L
P
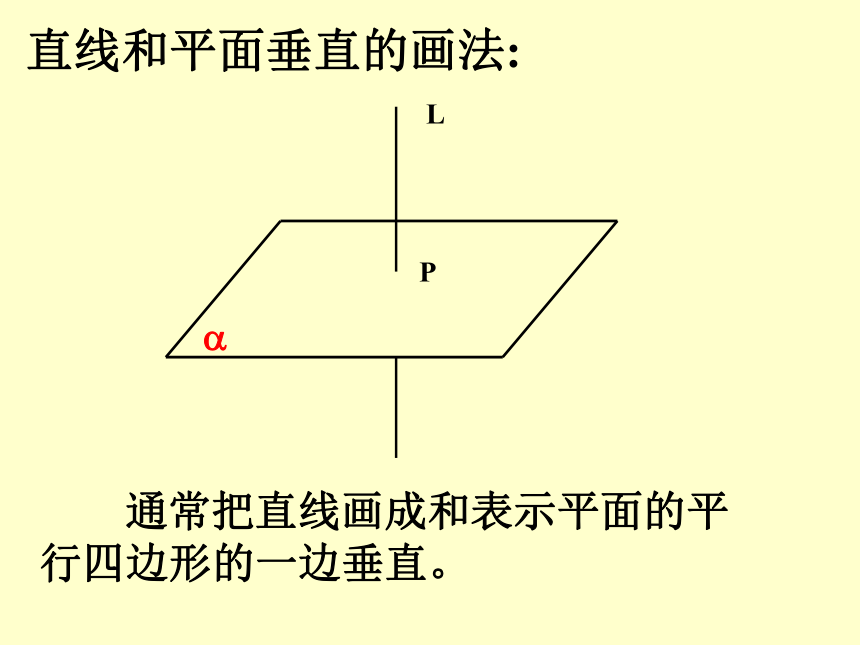
直线和平面垂直的画法:
通常把直线画成和表示平面的平行四边形的一边垂直。
深入理解“线面垂直定义”
辨析1判断下列语句是否正确:(若不正确请举反例)
2.如果一条直线与平面内无数条直线都垂直,那么它与平面垂直. ( )
1.如果一条直线与一个平面垂直,那么它与平面内所有的直线都垂直. ( )
b
α
a
利用定义,我们得到了判定线面垂直的最基本方法,同时也得到了线面垂直的最基本的性质.
探索新知:
但是,直接考察直线与平面内所有直线都垂直是不可能的,这就有必要去寻找比定义法更简捷、更可行的直线与平面垂直的方法!
分析实例—猜想定理
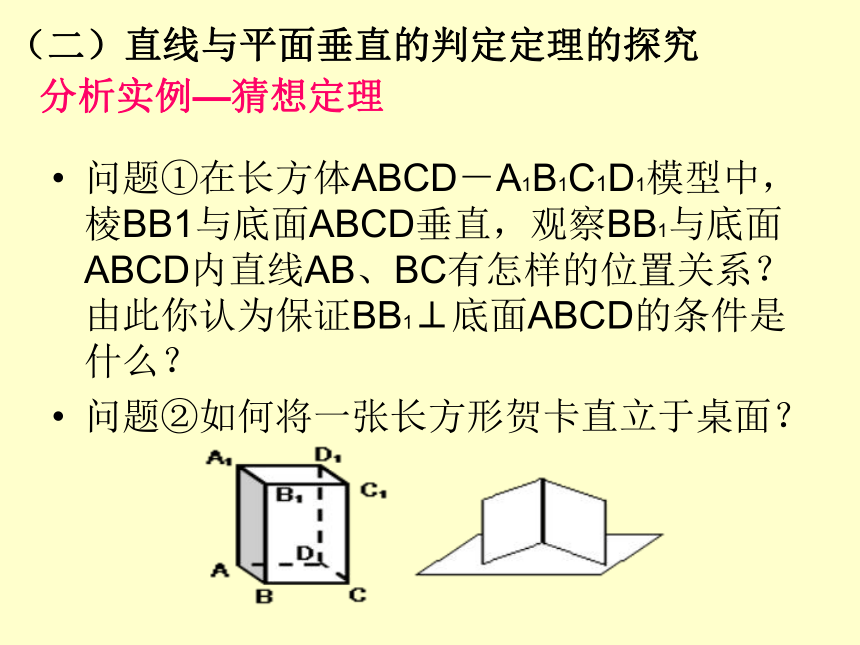
问题①在长方体ABCD-A1B1C1D1模型中,棱BB1与底面ABCD垂直,观察BB1与底面ABCD内直线AB、BC有怎样的位置关系?由此你认为保证BB1⊥底面ABCD的条件是什么?
问题②如何将一张长方形贺卡直立于桌面?
(二)直线与平面垂直的判定定理的探究
做一做
想一想
A
B
C
D
1.折痕AD与桌面垂直吗?
2.如何翻折才能使折痕AD与桌面所在的平面垂直?
请同学们拿出一块三角形纸片,我们一起做一个试验:过三角形的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触)
分析实例—猜想定理
当且仅当折痕 AD 是 BC 边上的高时,AD所在直线与桌面所在平面 垂直.
2.如何翻折才能使折痕AD与桌面所在的平面垂直?
分析实例—猜想定理
由刚才分析可以知道,直线与平面垂直的判定需要哪几个条件?
你能根据刚才的分析归纳出直线与平面垂
直判定定理吗
(1) 平面有两条直线
(2) 这两条直线要相交
(3) 平面外的直线要与这两条直线都垂直
分析实例—猜想定理
二、 直线与平面垂直的判定定理:
线线垂直 线面垂直
m
n
P
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
一相交两垂直
质疑反思—深化定理
辨析2:下列命题是否正确,为什么?
如果一条直线与平面内的两条平行直线都垂直,那么该直线垂直于这个平面。
例1 如图有一根旗杆AB高8m,它的顶端A挂有两条长10m的绳子,拉紧绳子并把它的下端放在地面上的两点(和旗杆脚不在同一条直线上)C、D。如果这两点都和旗杆脚B的距离是6m,那么旗杆就和地面垂直,为什么?
(三) 直线与平面垂直判定定理的初步应用
B
C
O
例2 求证:与三角形的两条边同时垂直的直线必与
第三条边垂直.
l
例3.如图,已知a∥b、a⊥α.
求证:b⊥α.
分析:在平面内作两条相交直线,由直线与平面垂直的定义可知,直线a与这两条相交直线是垂直的,又由b平行a,可证b与这两条相交直线也垂直,从而可证直线与平面垂直。
a
b
例3.如图,已知a∥b、a⊥α.
求证:b⊥α.
(线面垂直 线线垂直)
(线线垂直 线面垂直)
(四)总结反思—提高认识
(1)通过本节课的学习,你学会了哪些判断
直线与平面垂直的方法?
(2)在证明直线与平面垂直时应注意哪些问题?
(3)本节课涉及到哪些数学思想和方法?
(4)本节课你还有哪些问题?
直线与平面
垂直的判定
定义法
间接法
直接法
如果两条
平行直线中的
一条垂直于一
个平面,那么
另一条也垂直
于同一个平面。
如果一条直线垂于一个平面内的任何一条直线
此直线垂直于这个平面
判定定理
如果一条直线垂直于一个平面内的两条相交直线,那么此直线垂直于这个平面。
(1)
(2)数学思想方法:转化的思想
空间问题
平面问题
(五)布置作业—自主探究
必做题:如图(1),在三棱锥V-ABC中,VA=VC,
AB=BC,求证:VB⊥AC.
选做题:如图(2):SA平面ABC,ABBC,过A作SB的
垂线,垂足为E,过E作SC的垂线,垂足为F.求证:AFSC.
(1) (2)
(1) (2)
V
不去奋斗,不去创造,再美的青春也结不出硕果。
V
A
B
C
.
D
练习:
提示:找AC中点D,连接VD,BD
1.如图,在三棱锥V-ABC,VA=VC,AB=BC求证: VB⊥AC.
中
外
垂
3. 已知:如图 ,空间四边形 ABCD 中,
DB=DC,取 BC 中点 E,连接 AE、DE,
求证:BC⊥平面 AED.
证明:∵AB=AC,DB=DC,E 为BC 中点,
∴AE⊥BC,DE⊥BC.
又∵AE 与DE 交于E,∴BC⊥平面AED.
由判定定理可知要证明直
线垂直平面,只需证明直线与平面内的任意两
条相交直线垂直即可.
4:如图,点P 是平行四边形ABCD 所在平面外一点,O 是对角线AC与BD的交点,且PA =PC ,PB =PD .
求证:PO⊥平面ABCD
C
A
B
D
O
P
=
ABCD
PO
O
BD
AC
平面
又
^
\
I
Q
BD
PO
BD
O
PD
PB
的中点
是
点
又
^
\
=
Q
,
AC
PO
AC
O
PC
PA
的中点
是
点
证明
^
\
=
Q
,
P
A
B
C
O
5.如图,圆O所在一平面为 ,AB是圆O 的直径,C 在圆周上, 且PA AC, PA AB,
求证:(1)PA BC
(2)BC 平面PAC
证明:∵PA ⊥⊙O 所在平面,
BC?⊙O 所在平面,∴PA ⊥BC,
∵AB 为⊙O 直径, ∴AC⊥BC,
又 PA ∩AC=A, ∴BC⊥平面 PAC,
又 AE?平面 PAC,∴BC⊥AE,
∵AE⊥PC, PC∩BC=C,
∴AE⊥平面 PBC.
6.如图 6,已知 PA ⊥⊙O 所在平面,
AB 为⊙O 直径,C 是圆周上任一点,
过 A 作 AE⊥PC 于 E,求证:AE⊥平面 PBC.
7. 已知:正方体中,AC是面对角线,BD′是与AC 异面的体对角线.求证:AC⊥BD′
A
B
D
C
A′
B′
C
D
′
′
生活中有很多直线与平面垂直的实例,你能举出几个吗?
实例引入
旗杆与底面垂直
(一)平面垂直定义的建构
桥柱与水面的位置关系,给人以直线与平面垂直的形象.
思考1.阳光下直立于地面的旗杆及它在地面的影子有何位置关系.
A
B
α
1.旗杆所在的直线始终与
影子所在的直线垂直.
C1
B1
思考2 旗杆AB与地面内任意一条不过旗杆底部B的直线B1C1的位置关系又是什么?由此可以得到什么结论?
2.垂直.直线垂直于平面内的
任意一条直线.
如果直线 l 与平面 内的任意一条直线都垂直,我们说直线 l 与平面 互相垂直,
记作 .
平面 的垂线
直线 l 的垂面
垂足
直线与平面垂直
?
L
P
直线和平面垂直的画法:
通常把直线画成和表示平面的平行四边形的一边垂直。
深入理解“线面垂直定义”
辨析1判断下列语句是否正确:(若不正确请举反例)
2.如果一条直线与平面内无数条直线都垂直,那么它与平面垂直. ( )
1.如果一条直线与一个平面垂直,那么它与平面内所有的直线都垂直. ( )
b
α
a
利用定义,我们得到了判定线面垂直的最基本方法,同时也得到了线面垂直的最基本的性质.
探索新知:
但是,直接考察直线与平面内所有直线都垂直是不可能的,这就有必要去寻找比定义法更简捷、更可行的直线与平面垂直的方法!
分析实例—猜想定理
问题①在长方体ABCD-A1B1C1D1模型中,棱BB1与底面ABCD垂直,观察BB1与底面ABCD内直线AB、BC有怎样的位置关系?由此你认为保证BB1⊥底面ABCD的条件是什么?
问题②如何将一张长方形贺卡直立于桌面?
(二)直线与平面垂直的判定定理的探究
做一做
想一想
A
B
C
D
1.折痕AD与桌面垂直吗?
2.如何翻折才能使折痕AD与桌面所在的平面垂直?
请同学们拿出一块三角形纸片,我们一起做一个试验:过三角形的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触)
分析实例—猜想定理
当且仅当折痕 AD 是 BC 边上的高时,AD所在直线与桌面所在平面 垂直.
2.如何翻折才能使折痕AD与桌面所在的平面垂直?
分析实例—猜想定理
由刚才分析可以知道,直线与平面垂直的判定需要哪几个条件?
你能根据刚才的分析归纳出直线与平面垂
直判定定理吗
(1) 平面有两条直线
(2) 这两条直线要相交
(3) 平面外的直线要与这两条直线都垂直
分析实例—猜想定理
二、 直线与平面垂直的判定定理:
线线垂直 线面垂直
m
n
P
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
一相交两垂直
质疑反思—深化定理
辨析2:下列命题是否正确,为什么?
如果一条直线与平面内的两条平行直线都垂直,那么该直线垂直于这个平面。
例1 如图有一根旗杆AB高8m,它的顶端A挂有两条长10m的绳子,拉紧绳子并把它的下端放在地面上的两点(和旗杆脚不在同一条直线上)C、D。如果这两点都和旗杆脚B的距离是6m,那么旗杆就和地面垂直,为什么?
(三) 直线与平面垂直判定定理的初步应用
B
C
O
例2 求证:与三角形的两条边同时垂直的直线必与
第三条边垂直.
l
例3.如图,已知a∥b、a⊥α.
求证:b⊥α.
分析:在平面内作两条相交直线,由直线与平面垂直的定义可知,直线a与这两条相交直线是垂直的,又由b平行a,可证b与这两条相交直线也垂直,从而可证直线与平面垂直。
a
b
例3.如图,已知a∥b、a⊥α.
求证:b⊥α.
(线面垂直 线线垂直)
(线线垂直 线面垂直)
(四)总结反思—提高认识
(1)通过本节课的学习,你学会了哪些判断
直线与平面垂直的方法?
(2)在证明直线与平面垂直时应注意哪些问题?
(3)本节课涉及到哪些数学思想和方法?
(4)本节课你还有哪些问题?
直线与平面
垂直的判定
定义法
间接法
直接法
如果两条
平行直线中的
一条垂直于一
个平面,那么
另一条也垂直
于同一个平面。
如果一条直线垂于一个平面内的任何一条直线
此直线垂直于这个平面
判定定理
如果一条直线垂直于一个平面内的两条相交直线,那么此直线垂直于这个平面。
(1)
(2)数学思想方法:转化的思想
空间问题
平面问题
(五)布置作业—自主探究
必做题:如图(1),在三棱锥V-ABC中,VA=VC,
AB=BC,求证:VB⊥AC.
选做题:如图(2):SA平面ABC,ABBC,过A作SB的
垂线,垂足为E,过E作SC的垂线,垂足为F.求证:AFSC.
(1) (2)
(1) (2)
V
不去奋斗,不去创造,再美的青春也结不出硕果。
V
A
B
C
.
D
练习:
提示:找AC中点D,连接VD,BD
1.如图,在三棱锥V-ABC,VA=VC,AB=BC求证: VB⊥AC.
中
外
垂
3. 已知:如图 ,空间四边形 ABCD 中,
DB=DC,取 BC 中点 E,连接 AE、DE,
求证:BC⊥平面 AED.
证明:∵AB=AC,DB=DC,E 为BC 中点,
∴AE⊥BC,DE⊥BC.
又∵AE 与DE 交于E,∴BC⊥平面AED.
由判定定理可知要证明直
线垂直平面,只需证明直线与平面内的任意两
条相交直线垂直即可.
4:如图,点P 是平行四边形ABCD 所在平面外一点,O 是对角线AC与BD的交点,且PA =PC ,PB =PD .
求证:PO⊥平面ABCD
C
A
B
D
O
P
=
ABCD
PO
O
BD
AC
平面
又
^
\
I
Q
BD
PO
BD
O
PD
PB
的中点
是
点
又
^
\
=
Q
,
AC
PO
AC
O
PC
PA
的中点
是
点
证明
^
\
=
Q
,
P
A
B
C
O
5.如图,圆O所在一平面为 ,AB是圆O 的直径,C 在圆周上, 且PA AC, PA AB,
求证:(1)PA BC
(2)BC 平面PAC
证明:∵PA ⊥⊙O 所在平面,
BC?⊙O 所在平面,∴PA ⊥BC,
∵AB 为⊙O 直径, ∴AC⊥BC,
又 PA ∩AC=A, ∴BC⊥平面 PAC,
又 AE?平面 PAC,∴BC⊥AE,
∵AE⊥PC, PC∩BC=C,
∴AE⊥平面 PBC.
6.如图 6,已知 PA ⊥⊙O 所在平面,
AB 为⊙O 直径,C 是圆周上任一点,
过 A 作 AE⊥PC 于 E,求证:AE⊥平面 PBC.
7. 已知:正方体中,AC是面对角线,BD′是与AC 异面的体对角线.求证:AC⊥BD′
A
B
D
C
A′
B′
C
D
′
′
