2.3 幂函数 课件-人教版高中数学必修一(17张PPT)
文档属性
| 名称 | 2.3 幂函数 课件-人教版高中数学必修一(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 21:40:33 | ||
图片预览






文档简介
2.3 幂函数
以下函数有什么共同特征?
(1)均是以自变量为底的幂;
(2)指数为常数;
(3)自变量前面的系数为1;
(4)等号右边只有一项
都是形如y=xa的函数
y=x
y=x2
y=x3
y=x1/2
y=x-1
1
思考
幂函数的概念
一、幂函数的定义
一般地,函数 叫作(α次的)幂函数,其中x为自变量,α是常数.
典例展示
思考:幂函数 与指数函数 有何区别?
例1 判断下列函数哪些是幂函数?
(1) (2) (3)
(4) (5) (6)
(7) (8)
例2.已知函数 是幂函数,求m 的值
解:根据幂函数的定义得
得m=3或m=-2
思考:幂函数 与指数函数 有何区别?
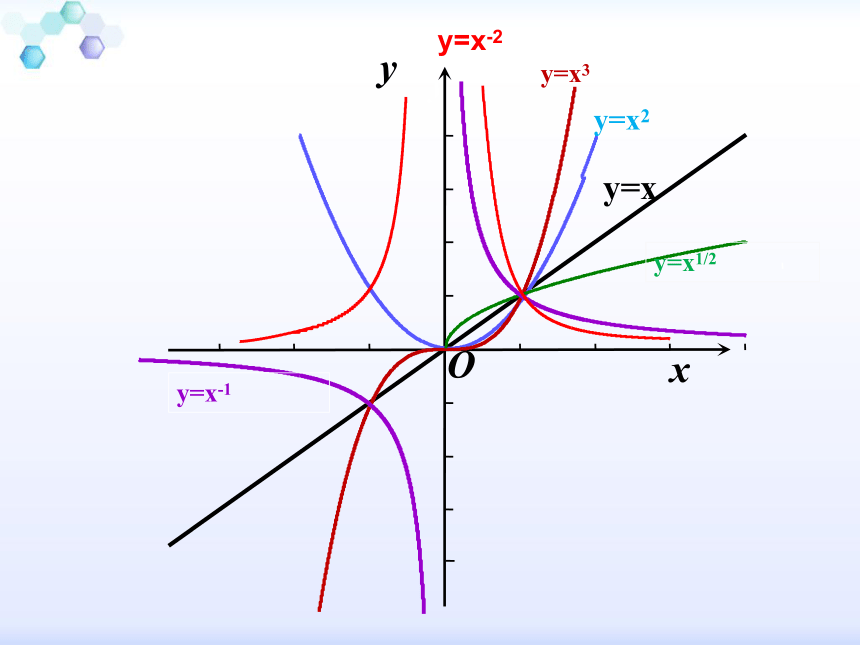
重点研究常见的六个幂函数y=x,y=x2,y=x3,y=x1/2,y=x-1,y=x-2的图象
幂函数的图象
y
x
y
O
y=x
y=x2
y=x3
y=x1/2
y=x-1
y=x-2
函数
性质
y=x
y=x2
y=x-1
y=x3
y=x-2
图像
定义域
值域
奇偶性
单调性
公共点
幂函数的性质
函数
性质
y=x
y=x2
y=x-1
y=x3
y=x-2
图像
定义域
值 域
奇偶性
单调性
公共点
幂函数的性质
R
R
奇
增
R
[0,+∞)
偶
[0,+∞)增
(-∞,0]增
R
R
奇
增
[0,+∞)
非奇非偶
[0,+∞)
增
{x|x≠0}
{y|y≠0}
奇
(0,+∞)和
(-∞,0)减
{x|x≠0}
(0,+∞)
(0,+∞)减
偶
(-∞,0)增
1
1
1
1
1
1
-
1
1
1
1
(1,1)
(1) 当α为奇数时,幂函数为奇函数;当α为偶数时,幂函数为偶函数.
幂函数的性质总结:
y
x
y
O
y=x
y=x2
y=x3
y=x1/2
y=x-1
y=x-2
(2) 所有的幂函数在(0,+∞)都有定义,并且图象都通过点(1,1),图像不过第四象限.
(4)当α>1时,若0 若x>1,则图像在y=x的下方;
当0<α<1时,若0 若x>1,则图像在y=x的下方;
幂函数的性质总结:
y
x
y
O
y=x
y=x2
y=x3
y=x1/2
α>1
0<α<1
1
1
(3) 如果α>0,则幂函数图象过(0,0)和(1,1),并且在区间[0,+∞)上是增函数;
课本P112
(5) 如果α<0,函数都过点(1,1),幂函数图象在区间(0,+∞)上是减函数;
图像向上与y轴无限的接近,向右与x轴无限的接近。
幂函数的性质总结:
y
x
y
O
y=x
y=x-1
y=x-2
α<0
1
1
课本P113
学以致用
例3 比较各组数的大小
1.比较大小
(1)
(2)
比较两个数大小的规律:
(1)若底数相同,利用指数函数的单调性比较大小;
(2)若指数相同,利用幂函数的单调性比较大小;
(3)若底数指数不同,通过中间量比较大小;
?
2.求参数
幂函数概念
幂函数图像
结构特征
作图识图
无图想图
不同指数对幂
函数性质的影响
应
用
幂函数性质
幂函数
作业布置
幂函数概念图象及性质的基础作业
以下函数有什么共同特征?
(1)均是以自变量为底的幂;
(2)指数为常数;
(3)自变量前面的系数为1;
(4)等号右边只有一项
都是形如y=xa的函数
y=x
y=x2
y=x3
y=x1/2
y=x-1
1
思考
幂函数的概念
一、幂函数的定义
一般地,函数 叫作(α次的)幂函数,其中x为自变量,α是常数.
典例展示
思考:幂函数 与指数函数 有何区别?
例1 判断下列函数哪些是幂函数?
(1) (2) (3)
(4) (5) (6)
(7) (8)
例2.已知函数 是幂函数,求m 的值
解:根据幂函数的定义得
得m=3或m=-2
思考:幂函数 与指数函数 有何区别?
重点研究常见的六个幂函数y=x,y=x2,y=x3,y=x1/2,y=x-1,y=x-2的图象
幂函数的图象
y
x
y
O
y=x
y=x2
y=x3
y=x1/2
y=x-1
y=x-2
函数
性质
y=x
y=x2
y=x-1
y=x3
y=x-2
图像
定义域
值域
奇偶性
单调性
公共点
幂函数的性质
函数
性质
y=x
y=x2
y=x-1
y=x3
y=x-2
图像
定义域
值 域
奇偶性
单调性
公共点
幂函数的性质
R
R
奇
增
R
[0,+∞)
偶
[0,+∞)增
(-∞,0]增
R
R
奇
增
[0,+∞)
非奇非偶
[0,+∞)
增
{x|x≠0}
{y|y≠0}
奇
(0,+∞)和
(-∞,0)减
{x|x≠0}
(0,+∞)
(0,+∞)减
偶
(-∞,0)增
1
1
1
1
1
1
-
1
1
1
1
(1,1)
(1) 当α为奇数时,幂函数为奇函数;当α为偶数时,幂函数为偶函数.
幂函数的性质总结:
y
x
y
O
y=x
y=x2
y=x3
y=x1/2
y=x-1
y=x-2
(2) 所有的幂函数在(0,+∞)都有定义,并且图象都通过点(1,1),图像不过第四象限.
(4)当α>1时,若0
当0<α<1时,若0
幂函数的性质总结:
y
x
y
O
y=x
y=x2
y=x3
y=x1/2
α>1
0<α<1
1
1
(3) 如果α>0,则幂函数图象过(0,0)和(1,1),并且在区间[0,+∞)上是增函数;
课本P112
(5) 如果α<0,函数都过点(1,1),幂函数图象在区间(0,+∞)上是减函数;
图像向上与y轴无限的接近,向右与x轴无限的接近。
幂函数的性质总结:
y
x
y
O
y=x
y=x-1
y=x-2
α<0
1
1
课本P113
学以致用
例3 比较各组数的大小
1.比较大小
(1)
(2)
比较两个数大小的规律:
(1)若底数相同,利用指数函数的单调性比较大小;
(2)若指数相同,利用幂函数的单调性比较大小;
(3)若底数指数不同,通过中间量比较大小;
?
2.求参数
幂函数概念
幂函数图像
结构特征
作图识图
无图想图
不同指数对幂
函数性质的影响
应
用
幂函数性质
幂函数
作业布置
幂函数概念图象及性质的基础作业
