数学人教A版(2019)必修第二册第八章 球的体积和表面积课件(共29张PPT)
文档属性
| 名称 | 数学人教A版(2019)必修第二册第八章 球的体积和表面积课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 24.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-30 08:54:05 | ||
图片预览








文档简介
球的体积和表面积
球体无处不在!
已知标准篮球的直径为24.6厘米,则制作和使用篮球往往需要考虑:
(1)制成一个篮球需要多少皮革?
(2)充满一个篮球需要多少气体?
如何计算球的表面积?
如何计算球的体积?
课前探究任务
请你观察一下生活中常见的球形物体,尝试测出其体积,你发现了什么规律?
回顾:球体的定义
回顾:球体的定义
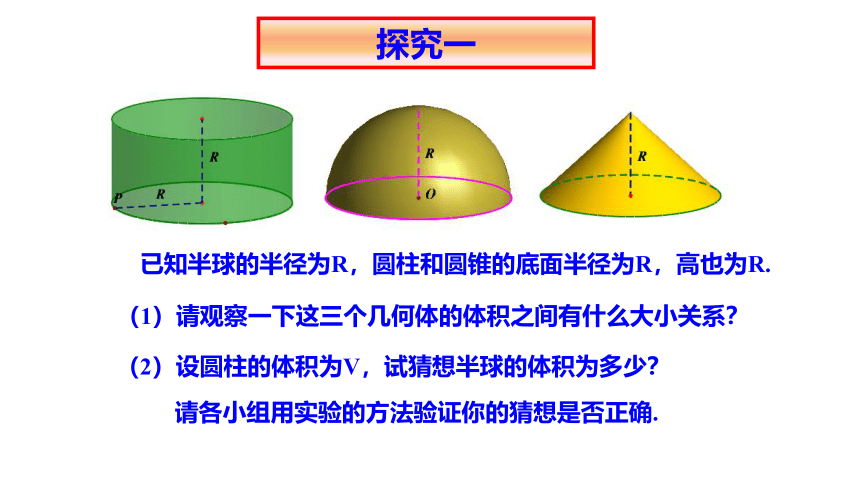
探究一
已知半球的半径为R,圆柱和圆锥的底面半径为R,高也为R.
(1)请观察一下这三个几何体的体积之间有什么大小关系?
(2)设圆柱的体积为V,试猜想半球的体积为多少?
请各小组用实验的方法验证你的猜想是否正确.
祖暅原理
祖冲之
祖暅(geng)
幂势即同
积不容异
祖暅,字景烁,是著名数学家祖冲之的儿子,也是南北朝时代的伟大科学家。他于5世纪末提出祖暅原理。在欧洲直到17世纪,才有意大利数学家卡瓦列里提出相关结论,比西方国家的数学家早一千多年。
祖暅原理
祖暅原理:夹在两个平行平面之间的两个几何体(它们的形状可以不同),被平行于这两个平面的任意平面所截,如果截面(阴影部分)的面积都相等,那么这两个几何体的体积一定相等。
祖冲之父子是我们中华民族的骄傲和自豪!
R
探究二
用平行于半球底面且与半球底面的距离为h的平面去截两个几何体,所截得的面积分别为S1,S2,试用R和h表示S1,S2,并说明它们有什么关系。
半径为R的球的体积
O R
割之弥细,失之弥少
割之又割,以至于不可割
则与圆合体,而无所失矣
刘徽割圆术
学生活动:切橙子
把半球分割成n个薄片
把半球分割成n个薄片
把半球分割成n个薄片
分割→取近似→求和→取极限
探究三
O
o
球的体积V可以如何表示?试着推导出球的表面积公式.
分割越细密,即n越大,每一片的顶点和球心的连线构成的几何体接近什么几何体?其体积Vi可以如何近似求解?请列式表示出来.
经线圈和纬线圈将球面分割成n片,这n片的面积分别记为S1, S2,…, Sn,球的表面积S与S1, S2,…, Sn有什么关系?
都是以R为自变量的函数
已知标准篮球的直径为24.6厘米,请大家计算篮球的表面积和体积。
例题:如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?(假设冰淇淋融化前后体积不变)
12 cm
4 cm
课堂小结
通过本节课的学习,你有什么体会和收获呢?
作业布置
必做题:课本 P29 习题1.3 B组 第1题;
思考题:
1. 请查阅资料,试着用微积分的方法推导球的体积公式。你还能想到别的推导球的体积和表面积的方法吗?
2. (1)把钢球放入一个正方体的有盖
纸盒中,已知正方体的棱长为a,求钢球
的最大半径为多少? (2)正方体的各个顶点都在一个球
的球面上,已知正方体的棱长为a,求
该球的半径为多少?
谢谢大家
球体无处不在!
已知标准篮球的直径为24.6厘米,则制作和使用篮球往往需要考虑:
(1)制成一个篮球需要多少皮革?
(2)充满一个篮球需要多少气体?
如何计算球的表面积?
如何计算球的体积?
课前探究任务
请你观察一下生活中常见的球形物体,尝试测出其体积,你发现了什么规律?
回顾:球体的定义
回顾:球体的定义
探究一
已知半球的半径为R,圆柱和圆锥的底面半径为R,高也为R.
(1)请观察一下这三个几何体的体积之间有什么大小关系?
(2)设圆柱的体积为V,试猜想半球的体积为多少?
请各小组用实验的方法验证你的猜想是否正确.
祖暅原理
祖冲之
祖暅(geng)
幂势即同
积不容异
祖暅,字景烁,是著名数学家祖冲之的儿子,也是南北朝时代的伟大科学家。他于5世纪末提出祖暅原理。在欧洲直到17世纪,才有意大利数学家卡瓦列里提出相关结论,比西方国家的数学家早一千多年。
祖暅原理
祖暅原理:夹在两个平行平面之间的两个几何体(它们的形状可以不同),被平行于这两个平面的任意平面所截,如果截面(阴影部分)的面积都相等,那么这两个几何体的体积一定相等。
祖冲之父子是我们中华民族的骄傲和自豪!
R
探究二
用平行于半球底面且与半球底面的距离为h的平面去截两个几何体,所截得的面积分别为S1,S2,试用R和h表示S1,S2,并说明它们有什么关系。
半径为R的球的体积
O R
割之弥细,失之弥少
割之又割,以至于不可割
则与圆合体,而无所失矣
刘徽割圆术
学生活动:切橙子
把半球分割成n个薄片
把半球分割成n个薄片
把半球分割成n个薄片
分割→取近似→求和→取极限
探究三
O
o
球的体积V可以如何表示?试着推导出球的表面积公式.
分割越细密,即n越大,每一片的顶点和球心的连线构成的几何体接近什么几何体?其体积Vi可以如何近似求解?请列式表示出来.
经线圈和纬线圈将球面分割成n片,这n片的面积分别记为S1, S2,…, Sn,球的表面积S与S1, S2,…, Sn有什么关系?
都是以R为自变量的函数
已知标准篮球的直径为24.6厘米,请大家计算篮球的表面积和体积。
例题:如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?(假设冰淇淋融化前后体积不变)
12 cm
4 cm
课堂小结
通过本节课的学习,你有什么体会和收获呢?
作业布置
必做题:课本 P29 习题1.3 B组 第1题;
思考题:
1. 请查阅资料,试着用微积分的方法推导球的体积公式。你还能想到别的推导球的体积和表面积的方法吗?
2. (1)把钢球放入一个正方体的有盖
纸盒中,已知正方体的棱长为a,求钢球
的最大半径为多少? (2)正方体的各个顶点都在一个球
的球面上,已知正方体的棱长为a,求
该球的半径为多少?
谢谢大家
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
