数学人教A版必修5章末解三角形中的范围问题(函数思想)比赛课件(共22张PPT)
文档属性
| 名称 | 数学人教A版必修5章末解三角形中的范围问题(函数思想)比赛课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-30 09:19:21 | ||
图片预览






文档简介
巧用函数思想——
解三角形中的范围问题
人教版高中必修5
高一年级微专题
=b2+c2-2bccos A
01
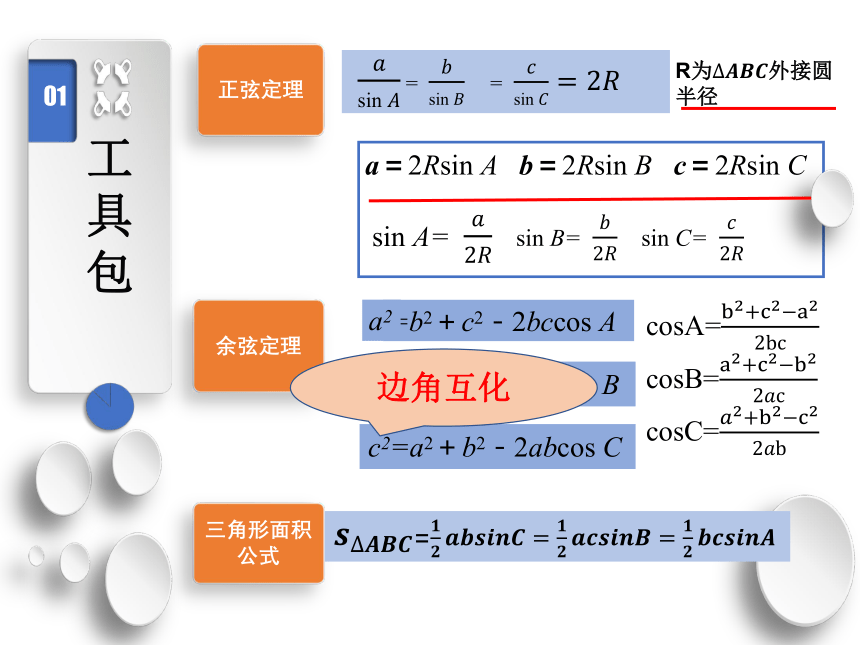
工具包
正弦定理
R为?????????????外接圆半径
?
a=2Rsin A b=2Rsin B c=2Rsin C
sin A= ????2???? sin B= ????2???????sin C= ????2????
?
余弦定理
b2=c2+a2-2cacos B
c2=a2+b2-2abcos C
三角形面积公式
a2
????sin????? = ????sin????????= ????sin?????=2????
?
cosA=b2+c2?a22bc
cosB=a2+c2?b22????c cosC=????2+b2?c22????b
?
?????????????????=????????????????????????????????=????????????????????????????????=????????????????????????????????
?
边角互化
巧用函数思想——
三角形中的范围问题
人教版高中必修5
高一年级微专题
新知学习
由????// ?????得?????????????????????????????+????????????????????=????
?
02
由正弦定理得sinBcosA-2sinCcosA+sinAcosB=0
即2sinCcosA=sin(A+B)
在⊿ABC中,由sinC>0
得cosA=??????????
?
由????∈(????,????)
?
分析:
=sinC
A=?????????
?
新知学习
B
02
A
C
B
????3
?
y=sinB+sinC
B+C=????????????
?
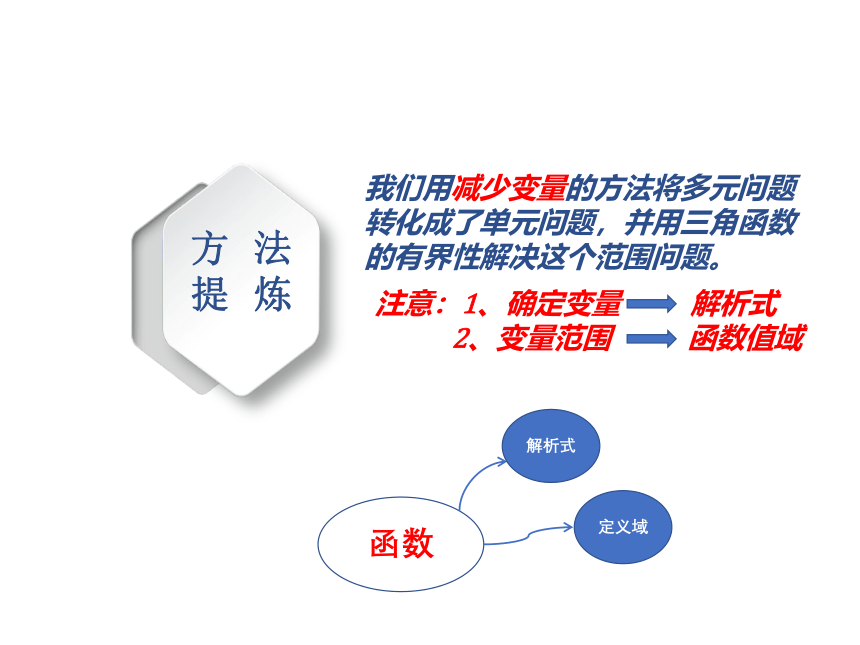
方法提炼
我们用减少变量的方法将多元问题转化成了单元问题,并用三角函数的有界性解决这个范围问题。
函数
解析式
定义域
注意:1、确定变量 解析式
2、变量范围 函数值域
若a=2,求⊿ABC周长的范围。
思维拔高
变式1
⊿ABC周长=a+b+c=2+b+c
32,3
?
=2+????????????????????????+????????????????
?
b=2Rsin B
c=2Rsin C
????????=????????????????????=????????????
?
=????+????????????(????????????????+????????????????)
?
∈4,????
?
03
=????+????????????????(????+????????)
?
边化角
三角函数
分析:
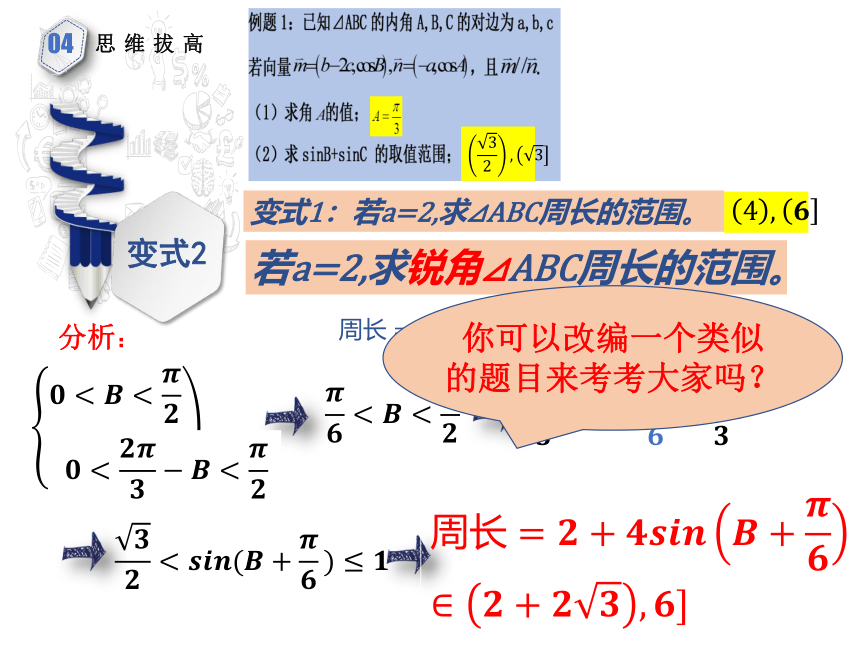
若a=2,求锐角⊿ABC周长的范围。
思维拔高
变式2
32,3
?
4,????
?
04
?
变式1:若a=2,求⊿ABC周长的范围。
?????
?????????
?????????
?????????
周长=????+????????????????????+????????∈????+????????,????]
?
周长=????+????????????????????+????????
?
分析:
你可以改编一个类似的题目来考考大家吗?
?????
方法提炼
我们用化归思想 ,并利用减少变量的方法将多元范围问题转化成了单元三角函数值域问题。
函数
解析式
定义域
注意:1、确定变量 解析式
2、变量范围 函数值域
追求卓越
自主探究:
05
C
B
A
追求卓越
自主探究:
05
由C=?????????+????=?????????????+????????=????????-2A
?
由C>????可得?????
将????=?????????????????代入可得sinA+sinC=sinA+sin(?????????????????)
?
=????????????????+????????????????????
?
=????????????????+?????????????????????????????
?
用换元法整理成二次函数
令????????????????=????,
?
????????=?????????????+????+????=?????(?????????????)????+????????
?
由????∈(????,????????) 可知????∈(????,????????)
?
∈(????????, ????????]
?
分析:
注意A的范围
走近高考
06
S?????????????=????????????????????????????????=????????????
?
由????????????????????=????????????????????有????=????????????????????????????????
?
=????????????????????????+????????????????????????????????????????
?
=????????????????????????????+????????
?
=????????????(?????????????????)????????????????
?
分析:
有????????????C> ????????
?
由?????????
∴0?
∴?????????
∴S?????????????∈(????????,????????)
?
三角函数
变量的范围
总结提炼
同学们,你们在这节课中学会了什么呢?
解决了什么问题:
用了什么思想方法:
追求卓越
自主探究:
05
A
C2
B
????3
?
1
C1
∟
∟
????????1?
12?
S?????????????=????????????
?
38?
课堂小结
我们本节课主要围绕了解三角形中的范围问题展开讨论。用化归思想化未知为已知并利用减少变量的方法将多元问题转化成了单元的函数问题。
函数
解析式
定义域
注意:1、确定变量 解析式
2、变量范围 定义域
航天工程离不开数学
人工智能离不开数学
大数据离不开数学
计算机编程离不开数学
课后巩固练习
谢谢聆听
成都石室白马中学
追求卓越
自主探究:
05
A
C2
B
????3
?
1
C1
∟
∟
????????1
解三角形中的范围问题
人教版高中必修5
高一年级微专题
=b2+c2-2bccos A
01
工具包
正弦定理
R为?????????????外接圆半径
?
a=2Rsin A b=2Rsin B c=2Rsin C
sin A= ????2???? sin B= ????2???????sin C= ????2????
?
余弦定理
b2=c2+a2-2cacos B
c2=a2+b2-2abcos C
三角形面积公式
a2
????sin????? = ????sin????????= ????sin?????=2????
?
cosA=b2+c2?a22bc
cosB=a2+c2?b22????c cosC=????2+b2?c22????b
?
?????????????????=????????????????????????????????=????????????????????????????????=????????????????????????????????
?
边角互化
巧用函数思想——
三角形中的范围问题
人教版高中必修5
高一年级微专题
新知学习
由????// ?????得?????????????????????????????+????????????????????=????
?
02
由正弦定理得sinBcosA-2sinCcosA+sinAcosB=0
即2sinCcosA=sin(A+B)
在⊿ABC中,由sinC>0
得cosA=??????????
?
由????∈(????,????)
?
分析:
=sinC
A=?????????
?
新知学习
B
02
A
C
B
????3
?
y=sinB+sinC
B+C=????????????
?
方法提炼
我们用减少变量的方法将多元问题转化成了单元问题,并用三角函数的有界性解决这个范围问题。
函数
解析式
定义域
注意:1、确定变量 解析式
2、变量范围 函数值域
若a=2,求⊿ABC周长的范围。
思维拔高
变式1
⊿ABC周长=a+b+c=2+b+c
32,3
?
=2+????????????????????????+????????????????
?
b=2Rsin B
c=2Rsin C
????????=????????????????????=????????????
?
=????+????????????(????????????????+????????????????)
?
∈4,????
?
03
=????+????????????????(????+????????)
?
边化角
三角函数
分析:
若a=2,求锐角⊿ABC周长的范围。
思维拔高
变式2
32,3
?
4,????
?
04
?
变式1:若a=2,求⊿ABC周长的范围。
?????
?????????
?????????
?????????
周长=????+????????????????????+????????∈????+????????,????]
?
周长=????+????????????????????+????????
?
分析:
你可以改编一个类似的题目来考考大家吗?
?????
方法提炼
我们用化归思想 ,并利用减少变量的方法将多元范围问题转化成了单元三角函数值域问题。
函数
解析式
定义域
注意:1、确定变量 解析式
2、变量范围 函数值域
追求卓越
自主探究:
05
C
B
A
追求卓越
自主探究:
05
由C=?????????+????=?????????????+????????=????????-2A
?
由C>????可得?????
将????=?????????????????代入可得sinA+sinC=sinA+sin(?????????????????)
?
=????????????????+????????????????????
?
=????????????????+?????????????????????????????
?
用换元法整理成二次函数
令????????????????=????,
?
????????=?????????????+????+????=?????(?????????????)????+????????
?
由????∈(????,????????) 可知????∈(????,????????)
?
∈(????????, ????????]
?
分析:
注意A的范围
走近高考
06
S?????????????=????????????????????????????????=????????????
?
由????????????????????=????????????????????有????=????????????????????????????????
?
=????????????????????????+????????????????????????????????????????
?
=????????????????????????????+????????
?
=????????????(?????????????????)????????????????
?
分析:
有????????????C> ????????
?
由?????????
∴0?
∴?????????
∴S?????????????∈(????????,????????)
?
三角函数
变量的范围
总结提炼
同学们,你们在这节课中学会了什么呢?
解决了什么问题:
用了什么思想方法:
追求卓越
自主探究:
05
A
C2
B
????3
?
1
C1
∟
∟
????????1?
12?
S?????????????=????????????
?
38?
课堂小结
我们本节课主要围绕了解三角形中的范围问题展开讨论。用化归思想化未知为已知并利用减少变量的方法将多元问题转化成了单元的函数问题。
函数
解析式
定义域
注意:1、确定变量 解析式
2、变量范围 定义域
航天工程离不开数学
人工智能离不开数学
大数据离不开数学
计算机编程离不开数学
课后巩固练习
谢谢聆听
成都石室白马中学
追求卓越
自主探究:
05
A
C2
B
????3
?
1
C1
∟
∟
????????1
