2020-2021学年八年级数学沪科版下册-18.1 勾股定理-教案
文档属性
| 名称 | 2020-2021学年八年级数学沪科版下册-18.1 勾股定理-教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-30 09:46:31 | ||
图片预览

文档简介
勾股定理
教学目标
知识与技能:掌握一个定理——勾股定理,并会用定理解决简单问题。
数学与思考:经历一次由特殊到一般的探索过程,通过观察,思考尝试猜想结论,发展合情推理能力。
解决问题:体验一种利用几何图形的面积证明代数恒等式的数、形结合的思想,感受数学思维的严谨性。
情感态度:对勾股定理历史的了解,感受数学文化,增添一份民族自豪感,在探究活动中培养学生的合作交流意识和探索精神。
重点难点
重点
勾股定理的证明与运用;
难点
用拼图法证明勾股定理。
教学方法
探究式教学。
教学过程:
情境引入
相传2500年前,古希腊有位著名的数学家——毕达哥拉斯.有一次在朋友家做客,当朋友们都在高谈阔论的时候,他却对着朋友家的地砖发呆.他发现其中以一个直角三角形的边长做出三个正方形,它们的面积之间似乎有着不平常的关系.
二、合作交流
第一关——观察猜想
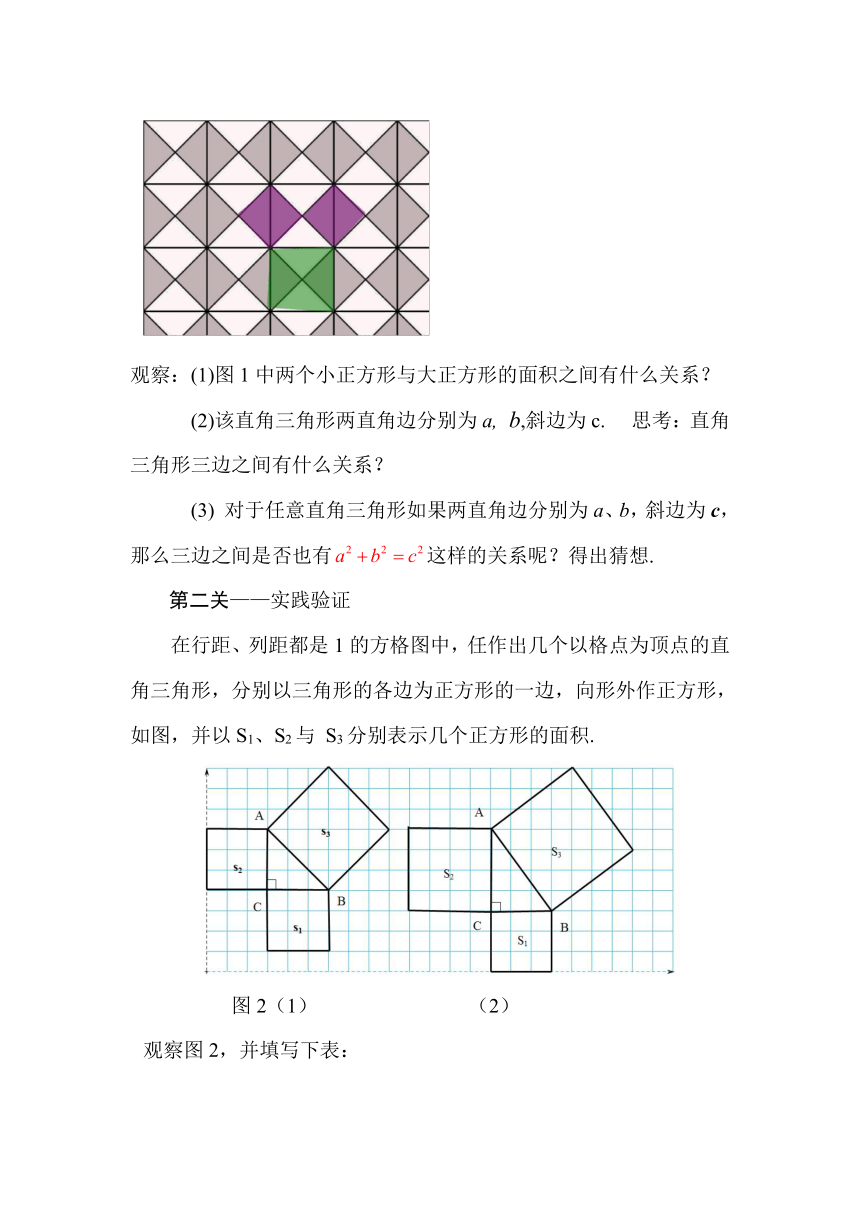
观察:(1)图1中两个小正方形与大正方形的面积之间有什么关系?
(2)该直角三角形两直角边分别为a,
b,斜边为c.
思考:直角三角形三边之间有什么关系?
(3)
对于任意直角三角形如果两直角边分别为a、b,斜边为c,那么三边之间是否也有这样的关系呢?得出猜想.
第二关——实践验证
在行距、列距都是1的方格图中,任作出几个以格点为顶点的直角三角形,分别以三角形的各边为正方形的一边,向形外作正方形,如图,并以S1、S2与
S3分别表示几个正方形的面积.
图2(1)
(2)
观察图2,并填写下表:
S1
S2
S1+S2
S3
图2(1)
图2(2)
图2(1)、(2)中三个正方形面积之间有怎样的关系呢?请用它们的边长表示.
师:用几何画板验证一下.
第三关——推论论证
用4个全等的直角三角形;拼成一个正方形,利用所拼的正方形的面积证明.
(
a
b
c
a
b
c
a
b
c
a
b
c
)
(分组讨论)
方法一:方法二:
勾股定理:直角三角形的直角边的平方和等于斜边的平方
如果直角三角形两直角边长分别为a、b,斜边长为c,那么
学以致用
四、视频欣赏
五、课堂小结
请谈谈你该节课有哪些收获?
六、小试牛刀
七、作业布置
课本P57
1,2
教学目标
知识与技能:掌握一个定理——勾股定理,并会用定理解决简单问题。
数学与思考:经历一次由特殊到一般的探索过程,通过观察,思考尝试猜想结论,发展合情推理能力。
解决问题:体验一种利用几何图形的面积证明代数恒等式的数、形结合的思想,感受数学思维的严谨性。
情感态度:对勾股定理历史的了解,感受数学文化,增添一份民族自豪感,在探究活动中培养学生的合作交流意识和探索精神。
重点难点
重点
勾股定理的证明与运用;
难点
用拼图法证明勾股定理。
教学方法
探究式教学。
教学过程:
情境引入
相传2500年前,古希腊有位著名的数学家——毕达哥拉斯.有一次在朋友家做客,当朋友们都在高谈阔论的时候,他却对着朋友家的地砖发呆.他发现其中以一个直角三角形的边长做出三个正方形,它们的面积之间似乎有着不平常的关系.
二、合作交流
第一关——观察猜想
观察:(1)图1中两个小正方形与大正方形的面积之间有什么关系?
(2)该直角三角形两直角边分别为a,
b,斜边为c.
思考:直角三角形三边之间有什么关系?
(3)
对于任意直角三角形如果两直角边分别为a、b,斜边为c,那么三边之间是否也有这样的关系呢?得出猜想.
第二关——实践验证
在行距、列距都是1的方格图中,任作出几个以格点为顶点的直角三角形,分别以三角形的各边为正方形的一边,向形外作正方形,如图,并以S1、S2与
S3分别表示几个正方形的面积.
图2(1)
(2)
观察图2,并填写下表:
S1
S2
S1+S2
S3
图2(1)
图2(2)
图2(1)、(2)中三个正方形面积之间有怎样的关系呢?请用它们的边长表示.
师:用几何画板验证一下.
第三关——推论论证
用4个全等的直角三角形;拼成一个正方形,利用所拼的正方形的面积证明.
(
a
b
c
a
b
c
a
b
c
a
b
c
)
(分组讨论)
方法一:方法二:
勾股定理:直角三角形的直角边的平方和等于斜边的平方
如果直角三角形两直角边长分别为a、b,斜边长为c,那么
学以致用
四、视频欣赏
五、课堂小结
请谈谈你该节课有哪些收获?
六、小试牛刀
七、作业布置
课本P57
1,2
