五年级下册数学教案 分数的意义 西师大版
文档属性
| 名称 | 五年级下册数学教案 分数的意义 西师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 20:38:32 | ||
图片预览




文档简介
分数的意义
教学目标:
结合具体情境,经历理解分数和单位“1”的意义过程,了解单位“1”在分数中的重要作用,渗透数形结合思想。
理解分数单位的意义,知道一个分数含有多少个分数单位。
结合具体情境,经历探究分数与除法的关系的过程,理解分数与除法的关系,会用分数表示除法的商。
理解并掌握求一个数是另一个数的几分之几的问题的解题方法,培养提出问题和解决问题的能力。
认识真分数和假分数的过程,理解真分数和假分数的意义,掌握它们各自的特征。
掌握将分子是分母的整数倍的分数转化成整数的方法。
重难点:
理解分数和分数单位的意义。
理解单位“1”的意义。
会用分数表示除法的商。
理解分数与除法的关系和区别。
理解真分数和假分数的意义,掌握将分子是分母的整数倍的分数转化成整数的方法,明确真分数和假分数的特征。
教学过程:
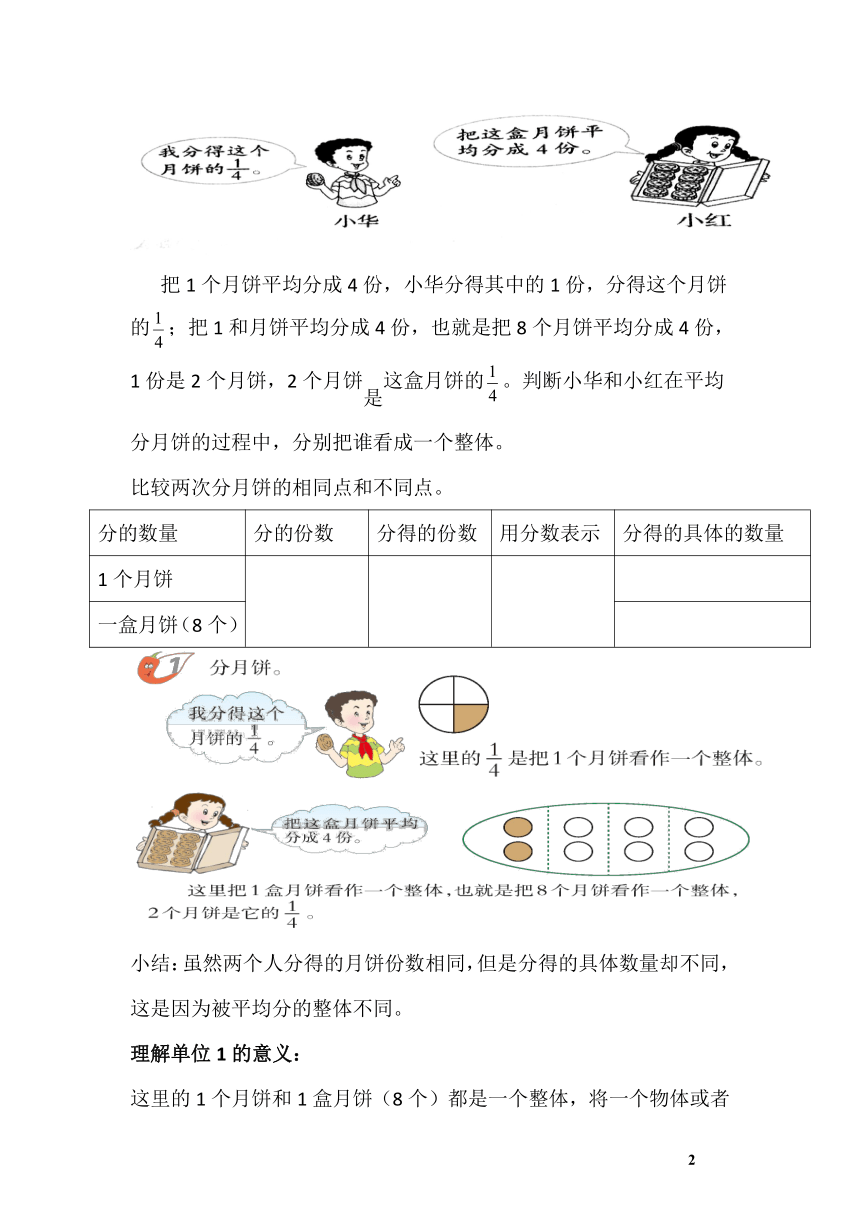
把1个月饼平均分成4份,小华分得其中的1份,分得这个月饼的;把1和月饼平均分成4份,也就是把8个月饼平均分成4份,1份是2个月饼,2个月饼是这盒月饼的。判断小华和小红在平均分月饼的过程中,分别把谁看成一个整体。
比较两次分月饼的相同点和不同点。
分的数量
分的份数
分得的份数
用分数表示
分得的具体的数量
1个月饼
一盒月饼(8个)
小结:虽然两个人分得的月饼份数相同,但是分得的具体数量却不同,这是因为被平均分的整体不同。
理解单位1的意义:
这里的1个月饼和1盒月饼(8个)都是一个整体,将一个物体或者许多物体看成一个整体,他可以用自然数1来表示,通常把它叫做单位“1”。
把20根小棒平均分成5份,每份都是20根小棒的,求其中的3份是20根小棒的几分之?
分数的意义:
把单位“1”平均分成若干份,表示其中的1份或者几份的数,叫做分数。
写分数的方法:
用平均分成的份数做分母,取的份数做分子。如:把20根小棒平均分成5份,分母就是5,取其中的3份,分子就是3,写成的分数就是。
理解分数单位的意义:
把单位“1”平均分成若干份数,表示其中的1份的数,叫做分数单位。如:............都是分数单位
拿出20根小棒,把它看做单位“1”,平均分成5份,其中的3份是20根小棒的。
的分数单位是(
)
里有(
)个这样的分数单位。
涂色表示下面的分数
(1)
是把单位“1”平均分成( )份,表示这样的(
)份的数。
(2)把全班同学平均分成6组,一个组的人数是全班人数(
),两个组的人数是全班人数( )。
探究分数单位的特点:
(1)、一个分数的分母是几,它的分数单位单位就是几分之几。最大的分数单位是,没有最小的分数单位。
、一个分数,分子是多少,就表示有多少个这样的分数单位。
、不同分母的分数,它们的分数单位不同,相同分母的分数,它们的分数单位相同。
分数单位不像整数、小数那样固定,它总是随着单位“1”被平均分成的份数的变化而变化。
一个分数的分母越大,分数单位越小;分母越小,分数单位反而越大。
练习:
一、填空。
、把一根4m长的绳子平均分成5段,每段占绳子全长的(
),这里把(
)看作单位“1”。
把一个西瓜平均切成8块,每块是这个西瓜的(
),这里的单位“1”是指(
)。
的分数单位是(
),里有(
)个这样的分数单位。
选择。
、在分数中,决定分数单位大小的是(
)。
分子
B、分母
C、单位“1”
分数单位是的分数有(
)。
A、8个
B、7个
C、无数个
、奇思和妙想一起写假期作业,奇思写了语文作业,妙想写了数学作业的,他们谁写的作业多?(
)。
奇思
B、妙想
C、一样多
D、无法比较
在下图中圈出表示相应的分数。
分数与除法的关系:
一条花边长4m;把它平均分成7份布置在学习园地,每份的长度是多少?
先填表,再说一说你发现了什么?
用除法表示
有分数表示
把1kg大米平均分成3份,每份有多少千克?
1÷3
把3个饼平均分成4份,每份有多少个?
发现:被除数相当于分数的分子,除数相当于分数的分母,除号相当于分数的分数线。
明确分数与除数的关系:
(1)分数与除法的关系。
用字母表示分数与除法的关系。
如果用a表示被除数,b表示除数,那么分数与除法的关系可以表示为:a÷b=(b≠0)。
分数与除法的区别。
分数不等同于除法。分数是一个数,除法是一种运算。
求一个数是另一个数的几分之几的问题解决方法:
一个数÷另一个数=,即比较量÷标准量=。
练习:
填空。
根据分数与除法的关系填一填。
(
)÷(
)=
(
)÷36=
9÷(
)=
13÷25=
kg表示把3kg平均分成(
)份,取其中的(
);也表示把(
)kg平均分成(
)份,取其中的(
)份。
一副扑克牌,红桃的张数占扑克牌总数的(
),大、小王是梅花张数的(
)。
月球的质量大约是地球质量的几分之几?
用分数表示下面各算式的商。
把分数改写成除法算式。
三、
生活应用题
(1)、五(1)班有女生23人,男生25人,女生占全班人数的几分之几?男生占全班人数的几分之几?
(2)17分钟是几分之几小时?
以1个圆为单位“1”,在下面的图中涂上颜色表示相应的分数。
想一想:每个分数里各有几个它的分数单位?
观察上面的图形,你发现了什么?
分数
概括特征
与“1”比较大小
比1小的分数
和1相等的分数
比1大的分数
真分数和假分数的意义及特征:
像这样,分子比分母小的分数叫做真分数。像这样,分子与分母相等或者分子比分母大的分数叫做假分数。假分数等于1或大于1。
发现:分子是分母的整数倍的假分数可以化成数。
填空:
分子是9的假分数有(
)个;分母是8的真分数有(
)个。
分数单位是的最大真分数是(
)。
在中,x是大于0的自然数,当x小于(
)时,是真分数;当x大于或等于(
)时,是假分数;当x是(
)的整数倍时,能化成整数。
假分数与整数的互化:
12
1
教学目标:
结合具体情境,经历理解分数和单位“1”的意义过程,了解单位“1”在分数中的重要作用,渗透数形结合思想。
理解分数单位的意义,知道一个分数含有多少个分数单位。
结合具体情境,经历探究分数与除法的关系的过程,理解分数与除法的关系,会用分数表示除法的商。
理解并掌握求一个数是另一个数的几分之几的问题的解题方法,培养提出问题和解决问题的能力。
认识真分数和假分数的过程,理解真分数和假分数的意义,掌握它们各自的特征。
掌握将分子是分母的整数倍的分数转化成整数的方法。
重难点:
理解分数和分数单位的意义。
理解单位“1”的意义。
会用分数表示除法的商。
理解分数与除法的关系和区别。
理解真分数和假分数的意义,掌握将分子是分母的整数倍的分数转化成整数的方法,明确真分数和假分数的特征。
教学过程:
把1个月饼平均分成4份,小华分得其中的1份,分得这个月饼的;把1和月饼平均分成4份,也就是把8个月饼平均分成4份,1份是2个月饼,2个月饼是这盒月饼的。判断小华和小红在平均分月饼的过程中,分别把谁看成一个整体。
比较两次分月饼的相同点和不同点。
分的数量
分的份数
分得的份数
用分数表示
分得的具体的数量
1个月饼
一盒月饼(8个)
小结:虽然两个人分得的月饼份数相同,但是分得的具体数量却不同,这是因为被平均分的整体不同。
理解单位1的意义:
这里的1个月饼和1盒月饼(8个)都是一个整体,将一个物体或者许多物体看成一个整体,他可以用自然数1来表示,通常把它叫做单位“1”。
把20根小棒平均分成5份,每份都是20根小棒的,求其中的3份是20根小棒的几分之?
分数的意义:
把单位“1”平均分成若干份,表示其中的1份或者几份的数,叫做分数。
写分数的方法:
用平均分成的份数做分母,取的份数做分子。如:把20根小棒平均分成5份,分母就是5,取其中的3份,分子就是3,写成的分数就是。
理解分数单位的意义:
把单位“1”平均分成若干份数,表示其中的1份的数,叫做分数单位。如:............都是分数单位
拿出20根小棒,把它看做单位“1”,平均分成5份,其中的3份是20根小棒的。
的分数单位是(
)
里有(
)个这样的分数单位。
涂色表示下面的分数
(1)
是把单位“1”平均分成( )份,表示这样的(
)份的数。
(2)把全班同学平均分成6组,一个组的人数是全班人数(
),两个组的人数是全班人数( )。
探究分数单位的特点:
(1)、一个分数的分母是几,它的分数单位单位就是几分之几。最大的分数单位是,没有最小的分数单位。
、一个分数,分子是多少,就表示有多少个这样的分数单位。
、不同分母的分数,它们的分数单位不同,相同分母的分数,它们的分数单位相同。
分数单位不像整数、小数那样固定,它总是随着单位“1”被平均分成的份数的变化而变化。
一个分数的分母越大,分数单位越小;分母越小,分数单位反而越大。
练习:
一、填空。
、把一根4m长的绳子平均分成5段,每段占绳子全长的(
),这里把(
)看作单位“1”。
把一个西瓜平均切成8块,每块是这个西瓜的(
),这里的单位“1”是指(
)。
的分数单位是(
),里有(
)个这样的分数单位。
选择。
、在分数中,决定分数单位大小的是(
)。
分子
B、分母
C、单位“1”
分数单位是的分数有(
)。
A、8个
B、7个
C、无数个
、奇思和妙想一起写假期作业,奇思写了语文作业,妙想写了数学作业的,他们谁写的作业多?(
)。
奇思
B、妙想
C、一样多
D、无法比较
在下图中圈出表示相应的分数。
分数与除法的关系:
一条花边长4m;把它平均分成7份布置在学习园地,每份的长度是多少?
先填表,再说一说你发现了什么?
用除法表示
有分数表示
把1kg大米平均分成3份,每份有多少千克?
1÷3
把3个饼平均分成4份,每份有多少个?
发现:被除数相当于分数的分子,除数相当于分数的分母,除号相当于分数的分数线。
明确分数与除数的关系:
(1)分数与除法的关系。
用字母表示分数与除法的关系。
如果用a表示被除数,b表示除数,那么分数与除法的关系可以表示为:a÷b=(b≠0)。
分数与除法的区别。
分数不等同于除法。分数是一个数,除法是一种运算。
求一个数是另一个数的几分之几的问题解决方法:
一个数÷另一个数=,即比较量÷标准量=。
练习:
填空。
根据分数与除法的关系填一填。
(
)÷(
)=
(
)÷36=
9÷(
)=
13÷25=
kg表示把3kg平均分成(
)份,取其中的(
);也表示把(
)kg平均分成(
)份,取其中的(
)份。
一副扑克牌,红桃的张数占扑克牌总数的(
),大、小王是梅花张数的(
)。
月球的质量大约是地球质量的几分之几?
用分数表示下面各算式的商。
把分数改写成除法算式。
三、
生活应用题
(1)、五(1)班有女生23人,男生25人,女生占全班人数的几分之几?男生占全班人数的几分之几?
(2)17分钟是几分之几小时?
以1个圆为单位“1”,在下面的图中涂上颜色表示相应的分数。
想一想:每个分数里各有几个它的分数单位?
观察上面的图形,你发现了什么?
分数
概括特征
与“1”比较大小
比1小的分数
和1相等的分数
比1大的分数
真分数和假分数的意义及特征:
像这样,分子比分母小的分数叫做真分数。像这样,分子与分母相等或者分子比分母大的分数叫做假分数。假分数等于1或大于1。
发现:分子是分母的整数倍的假分数可以化成数。
填空:
分子是9的假分数有(
)个;分母是8的真分数有(
)个。
分数单位是的最大真分数是(
)。
在中,x是大于0的自然数,当x小于(
)时,是真分数;当x大于或等于(
)时,是假分数;当x是(
)的整数倍时,能化成整数。
假分数与整数的互化:
12
1
