2020-2021学年人教五四新版六年级(下)期中数学复习试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年人教五四新版六年级(下)期中数学复习试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 254.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 00:00:00 | ||
图片预览




文档简介
2020-2021学年人教五四新版六年级(下)期中数学复习试卷
一.选择题(共5小题,满分10分,每小题2分)
1.有两个正数a,b,且a<b,把大于等于a且小于等于b的所有数记作[a,b].例如,大于等于1且小于等于4的所有数记作[1,4].若整数m在[5,15]内,整数n在[﹣30,﹣20]内,那么的一切值中属于整数的个数为( )
A.5个
B.4个
C.3个
D.2个
2.如图,正方形ABCD的边长为3cm,以直线AB为轴,将正方形旋转一周,所得几何体的主视图的面积是( )
A.9cm2
B.9πcm2
C.18πcm2
D.18cm2
3.货车每次运货吨数、运货次数和运货总吨数这三种量中,成反比例的是( )
A.货车每次运货吨数一定,运货次数和运货总吨数
B.货车运货次数一定,每次运货吨数和运货总吨数
C.货车运货总吨数一定,每次运货吨数和运货次数
4.下列说法错误的是( )
A.若棱柱的底面边长相等,则它的各个侧面的面积相等
B.正九棱柱有9条侧棱,9个侧面,侧面为长方形
C.长方体、正方体都是棱柱
D.三棱柱的侧面为三角形
5.2021减去它的,再减去余下的,再减去余下的,…,以此类推,一直减到余下的,则最后剩下的数是( )
A.0
B.1
C.
D.
二.填空题(共7小题,满分14分,每小题2分)
6.在树上有一只蜗牛,白天向上挪动7cm,记为+7cm,晚间向下掉了3cm,可记作
cm.
7.如图,从一块边长为2的等边三角形卡纸上剪下一个面积最大的扇形,并将其围成一个圆锥,则圆锥的底面圆的半径是
.
8.某快餐店外卖促销,佳佳和点点想点外卖,每单需支付送餐费5元,每种餐食外卖价格如表:
餐食种类
价格(单位:元)
汉堡套餐
40
鸡翅
16
鸡块
15
冰激凌
14
蔬菜沙拉
9
促销活动:
(1)汉堡套餐5折优惠,每单仅限一套;
(2)全部商品(包括打折套餐)满20元减4元.满40元减10元,满60元减15元,满80元减20元.
佳佳想要汉堡套餐、鸡翅、冰激凌、蔬菜沙拉各一份;点点想要汉堡套餐、鸡块、冰激凌各一份,若他们把想要的都买全,最少要花
元(含送餐费).
9.把:0.75化成最简整数比为
.
10.一个比例中,两个内项都是6,而且两个比的比值都是5,其中一个外项为x,则x的值为
.
11.一个比例中,两个外项互为倒数,那么两个内项的积是
.
12.2019年6月,华为第二颗自研7纳米麒麟系列芯片810出炉,7纳米换算为米等于
米(用科学记数法表示)单位换算方法:1毫米=1000微米,1微米=1000纳米.
三.填空题(共9小题,满分20分)
13.如果节约20元钱,记作“+20”元,那么浪费15元钱,记作
元.
14.计算:9÷÷
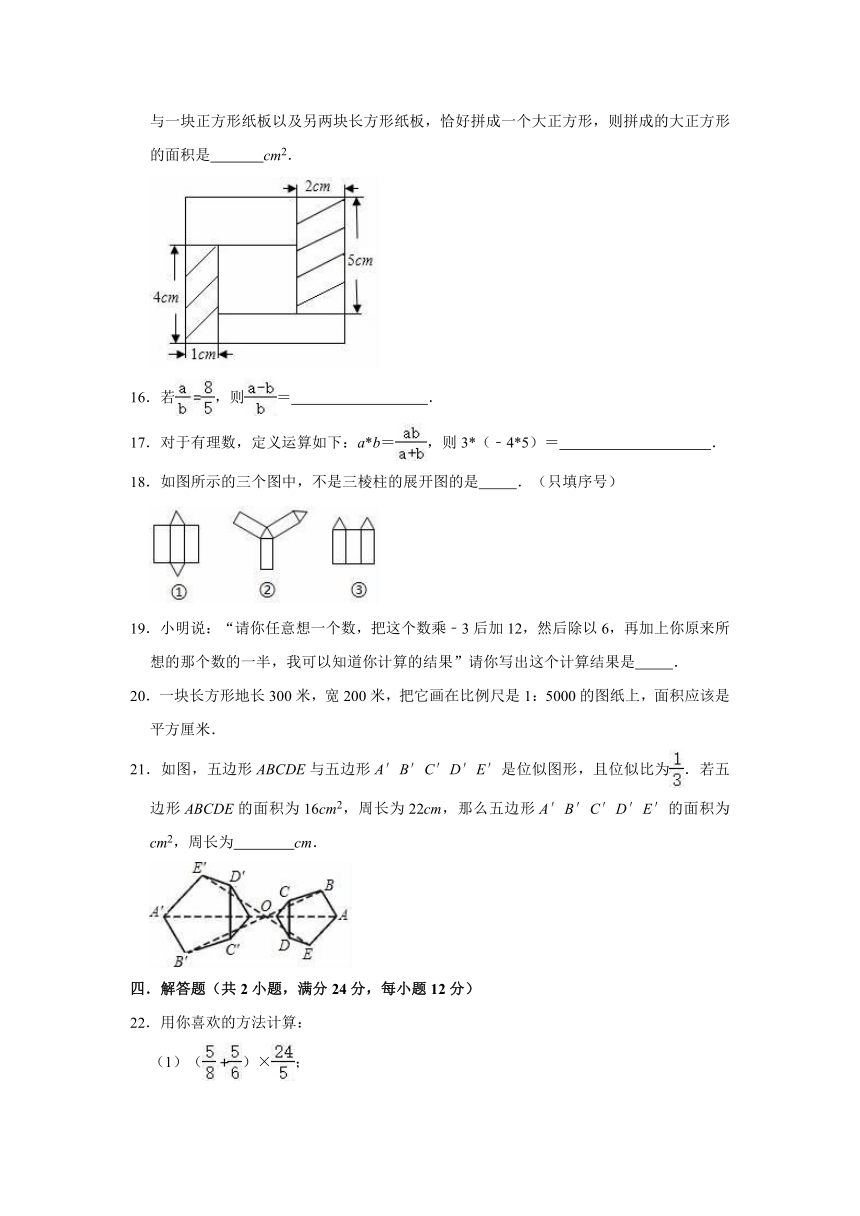
15.如图,用一块长5cm、宽2cm的长方形纸板,和一块长4cm、宽1cm的长方形纸板,与一块正方形纸板以及另两块长方形纸板,恰好拼成一个大正方形,则拼成的大正方形的面积是
cm2.
16.若,则=
.
17.对于有理数,定义运算如下:a
b=,则3
(﹣4
5)=
.
18.如图所示的三个图中,不是三棱柱的展开图的是
.(只填序号)
19.小明说:“请你任意想一个数,把这个数乘﹣3后加12,然后除以6,再加上你原来所想的那个数的一半,我可以知道你计算的结果”请你写出这个计算结果是
.
20.一块长方形地长300米,宽200米,把它画在比例尺是1:5000的图纸上,面积应该是
平方厘米.
21.如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,且位似比为.若五边形ABCDE的面积为16cm2,周长为22cm,那么五边形A′B′C′D′E′的面积为
cm2,周长为
cm.
四.解答题(共2小题,满分24分,每小题12分)
22.用你喜欢的方法计算:
(1)()×;
(2)×.
23.若某数除以4再减去2,等于这个数的加上8,求这个数.
五.解答题(共6小题,满分32分)
24.“赶陀螺”是一项深受人们喜爱的民族性运动,如图所示是一个陀螺的立体结构图.已知底面圆的直径AB=8cm,圆柱体部分的高BC=6cm,圆锥体部分的高CD=3cm,求出这个陀螺的表面积(结果保留π).
25.列方程解应用题:如图,现有两条乡村公路AB、BC,AB长为1200米,BC长为1600米,一个人骑摩托车从A处以20m/s的速度匀速沿公路AB、BC向C处行驶;另一人骑自行车从B处以5m/s的速度从B向C行驶,并且两人同时出发.
(1)求经过多少秒摩托车追上自行车?
(2)求两人均在行驶途中时,经过多少秒两人在行进路线上相距150米?
26.计算:
(1)2×(﹣3)3﹣4×(﹣3);
(2)﹣22÷(﹣)×(﹣).
27.某水果销售店用1000元购进甲、乙两种水果共140千克,这两种水果的进价、售价如下表所示:
进价(元/千克)
售价(元/千克)
甲种水果
5
8
乙种水果
9
13
(1)这两种水果各购进多少千克?
(2)若该水果店把这两种水果全部售完,则可获利多少元.
28.计算:(﹣1)2﹣|﹣3|+(﹣5)÷(﹣).
29.在一张地图上量得上海与南京两地的距离为3.2厘米,又已知上海与南京、北京两地的实际距离分别约为300千米和1080千米,那么在这张地图上,上海与北京两地的距离为多少厘米?
参考答案与试题解析
一.选择题(共5小题,满分10分,每小题2分)
1.解:∵m在[5,15]内,n在[﹣30,﹣20]内,
∴5≤m≤15,﹣30≤n≤﹣20,
∴≤≤,即﹣6≤≤﹣,
∴的一切值中属于整数的有﹣2,﹣3,﹣4,﹣5,﹣6,共5个;
故选:A.
2.解:所得几何体的主视图的面积是2×3×3=18cm2.
故选:D.
3.解:A、因为:运货总吨数÷运货次数=每次运货吨数(一定),所以运货次数和运货总吨数成正比例,不合题意;
B、因为:运货总吨数÷每次运货吨数=运货次数(一定),所以每次运货的吨数和运货总吨数成正比例,不合题意;
C、因为:每次运货的吨数×运货的次数=运货总吨数(一定),所以每次运货的吨数和运货的次数成反比例,符合题意;
故选:C.
4.解:(1)若棱柱的底面边长相等,则它的各个侧面的面积相等,这种说法正确,
(2)正九棱柱有9条侧棱,9个侧面,侧面为长方形,这种说法正确,
(3)长方体、正方体都是棱柱,这种说法正确,
(4)三棱柱的侧面为三角形,这种说法不正确,侧面为矩形,
故选:D.
5.解:由题意可得,
第一次剩下:2021﹣2021×=,
第二次剩下:×(1﹣)=×=,
第三次剩下:×(1﹣)==,
…,
∴一直减到余下的,最后剩下的数是=1,
故选:B.
二.填空题(共7小题,满分14分,每小题2分)
6.解:∵向上挪动7cm,记为+7cm,
∴向下掉了3cm,可记作﹣3cm.
故答案为:﹣3.
7.解:连接AD,
∵△ABC是边长为2的等边三角形,
∴AD=2×=,
∴扇形的弧长为=π,
∴圆锥的底面圆的半径是π÷π÷2=.
故答案为:.
8.解:由题意可得,
佳佳和点点合买一单的花费为:(40+40×0.5)+16+15+14×2+9=128(元),
佳佳和点点合买一单的实际消费为:128﹣20+5=113(元);
佳佳买全需要的物品需要花费:40×0.5+16+14+9=59(元),
佳佳实际花费为:59﹣10+5=54(元),
点点买全需要的物品需要花费:40×0.5+15+14=49(元),
点点实际花费为:49﹣10+5=44(元),
若他们把想要的都买全,最少要花55+44=98(元);
当佳佳和点点各买一单,佳佳买一单点汉堡套餐、鸡翅、冰激凌、鸡块,共需20+16+15+14=65(元),实际消费为:65﹣15+5=55(元),点点买一单点汉堡套餐、冰淇淋、蔬菜沙拉,共需20+14+9=43(元),实际消费为43﹣10+5=38(元),若他们把想要的都买全,最少要花55+38=93(元);
∵113>98>93,
∴他们最少要花93元,
故答案为:93.
9.解::0.75
=×
=8:9.
故答案为:8:9.
10.解:第一个比的前项为:5×6=30或6÷5=1.2;
∴这个比例为:30:6=6:x或1.2:6=6:x,
30x=36或1.2x=36,
解得x=1.2或x=30.
故答案为:1.2或30.
11.解:两个外项互为倒数则乘积是1,
因为比例中内项之积等于外项之积,
所以两个内项的积也是1.
故答案为:1.
12.解:7纳米=0.000000007米=7×10﹣9米,
故答案为7×10﹣9.
三.填空题(共9小题,满分20分)
13.解:∵节约20元钱,记作“+20”元,
∴浪费15元钱,记作﹣15元.
故答案为:﹣15.
14.解:原式=9××
=12×
=16.
15.解:设小正方形的边长为xcm,则大正方形的边长为4+(5﹣x)厘米或(x+1+2)厘米,
根据题意得:4+(5﹣x)=(x+1+2),
解得:x=3,
∴4+(5﹣x)=6,
∴大正方形的面积为36平方厘米.
答:大正方形的面积为36平方厘米.
故答案为:36.
16.解:∵,
∴a=b,
则==.
故答案为:.
17.解:∵a
b=,
∴3
(﹣4
5)
=3
=3
=3
(﹣20)
=
=
=,
故答案为:.
18.解:三棱柱的两底展开是在矩形两端各有一个三角形,侧面展开是三个矩形,
所以不是三棱柱的展开图的是③.
故答案为:③.
19.解:设所想的数为x,
根据题意,得
(﹣3x+12)+x
=﹣x+2+x
=2.
故答案为2.
20.解:∵比例尺是1:5000,长方形地长300米,宽200米,
∴图上长为300×=0.06(米),
0.06米=6厘米,
图上宽为200×=0.04(米),
0.04米=4厘米,
∴图上面积为6×4=24(平方厘米).
故答案为:24.
21.解:∵五边形ABCDE与五边形A′B′C′D′E′是位似图形,
∴五边形ABCDE∽五边形A′B′C′D′E′.
∴五边形ABCDE与五边形A′B′C′D′E′的周长比等于相似比,面积比等于相似比的平方.
∵位似比为.若五边形ABCDE的面积为16cm2,周长为22cm,
∴五边形A′B′C′D′E′的面积为144cm2,周长为66cm.
故五边形A′B′C′D′E′的面积为144cm2,周长为66cm.
故答案为:144,66.
四.解答题(共2小题,满分24分,每小题12分)
22.解:(1)()×
=××
=3+4
=7;
(2)×
=×+×
=(+)×
=1×
=.
23.解:设这个数为x,根据题意可得:
x÷4﹣2=x+8,
解得:x=﹣120,
答:这个数是﹣120.
五.解答题(共6小题,满分32分)
24.解:根据题意,圆柱的底面积=π×42=16π,
圆柱的侧面积=2π×4×6=48π,
圆锥的母线长为=5,
所以圆锥的侧面积=×2π×4×5=20π,
所以这个陀螺的表面积=16π+48π+20π=84π(cm2).
25.解:(1)设经过x秒摩托车追上自行车,
20x=5x+1200,
解得x=80.
答:经过80秒摩托车追上自行车.
(2)(1200+1600)÷20=140(秒).
设经过y秒两人相距150米,
第一种情况:摩托车还差150米追上自行车时,
20y﹣1200=5y﹣150
解得y=70,符合题意.
第二种情况:摩托车超过自行车150米时,
20y=150+5y+1200
解得y=90,符合题意.
答:经过70秒或90秒两人在行进路线上相距150米.
26.解:(1)原式=2×(﹣27)+12
=﹣54+12
=﹣42;
(2)原式=﹣4÷×(﹣)
=﹣24×(﹣)
=15.
27.解:(1)设购进甲种水果x千克,则购进乙种水果(140﹣x)千克,根据题意得:5x+9(140﹣x)=1000,
解得:x=65,
∴140﹣x=75.
答:购进甲种水果65千克,乙种水果75千克;
(2)(8﹣5)×65+(13﹣9)×75=495(元)
答:利润为495元.
28.解:原式=1﹣3+3=1.
29.解:设在这张地图上,上海与北京两地的距离为x厘米.根据题意得到:.
解得x=11.52,
答:在这张地图上,上海与北京两地的距离为11.52厘米.
一.选择题(共5小题,满分10分,每小题2分)
1.有两个正数a,b,且a<b,把大于等于a且小于等于b的所有数记作[a,b].例如,大于等于1且小于等于4的所有数记作[1,4].若整数m在[5,15]内,整数n在[﹣30,﹣20]内,那么的一切值中属于整数的个数为( )
A.5个
B.4个
C.3个
D.2个
2.如图,正方形ABCD的边长为3cm,以直线AB为轴,将正方形旋转一周,所得几何体的主视图的面积是( )
A.9cm2
B.9πcm2
C.18πcm2
D.18cm2
3.货车每次运货吨数、运货次数和运货总吨数这三种量中,成反比例的是( )
A.货车每次运货吨数一定,运货次数和运货总吨数
B.货车运货次数一定,每次运货吨数和运货总吨数
C.货车运货总吨数一定,每次运货吨数和运货次数
4.下列说法错误的是( )
A.若棱柱的底面边长相等,则它的各个侧面的面积相等
B.正九棱柱有9条侧棱,9个侧面,侧面为长方形
C.长方体、正方体都是棱柱
D.三棱柱的侧面为三角形
5.2021减去它的,再减去余下的,再减去余下的,…,以此类推,一直减到余下的,则最后剩下的数是( )
A.0
B.1
C.
D.
二.填空题(共7小题,满分14分,每小题2分)
6.在树上有一只蜗牛,白天向上挪动7cm,记为+7cm,晚间向下掉了3cm,可记作
cm.
7.如图,从一块边长为2的等边三角形卡纸上剪下一个面积最大的扇形,并将其围成一个圆锥,则圆锥的底面圆的半径是
.
8.某快餐店外卖促销,佳佳和点点想点外卖,每单需支付送餐费5元,每种餐食外卖价格如表:
餐食种类
价格(单位:元)
汉堡套餐
40
鸡翅
16
鸡块
15
冰激凌
14
蔬菜沙拉
9
促销活动:
(1)汉堡套餐5折优惠,每单仅限一套;
(2)全部商品(包括打折套餐)满20元减4元.满40元减10元,满60元减15元,满80元减20元.
佳佳想要汉堡套餐、鸡翅、冰激凌、蔬菜沙拉各一份;点点想要汉堡套餐、鸡块、冰激凌各一份,若他们把想要的都买全,最少要花
元(含送餐费).
9.把:0.75化成最简整数比为
.
10.一个比例中,两个内项都是6,而且两个比的比值都是5,其中一个外项为x,则x的值为
.
11.一个比例中,两个外项互为倒数,那么两个内项的积是
.
12.2019年6月,华为第二颗自研7纳米麒麟系列芯片810出炉,7纳米换算为米等于
米(用科学记数法表示)单位换算方法:1毫米=1000微米,1微米=1000纳米.
三.填空题(共9小题,满分20分)
13.如果节约20元钱,记作“+20”元,那么浪费15元钱,记作
元.
14.计算:9÷÷
15.如图,用一块长5cm、宽2cm的长方形纸板,和一块长4cm、宽1cm的长方形纸板,与一块正方形纸板以及另两块长方形纸板,恰好拼成一个大正方形,则拼成的大正方形的面积是
cm2.
16.若,则=
.
17.对于有理数,定义运算如下:a
b=,则3
(﹣4
5)=
.
18.如图所示的三个图中,不是三棱柱的展开图的是
.(只填序号)
19.小明说:“请你任意想一个数,把这个数乘﹣3后加12,然后除以6,再加上你原来所想的那个数的一半,我可以知道你计算的结果”请你写出这个计算结果是
.
20.一块长方形地长300米,宽200米,把它画在比例尺是1:5000的图纸上,面积应该是
平方厘米.
21.如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,且位似比为.若五边形ABCDE的面积为16cm2,周长为22cm,那么五边形A′B′C′D′E′的面积为
cm2,周长为
cm.
四.解答题(共2小题,满分24分,每小题12分)
22.用你喜欢的方法计算:
(1)()×;
(2)×.
23.若某数除以4再减去2,等于这个数的加上8,求这个数.
五.解答题(共6小题,满分32分)
24.“赶陀螺”是一项深受人们喜爱的民族性运动,如图所示是一个陀螺的立体结构图.已知底面圆的直径AB=8cm,圆柱体部分的高BC=6cm,圆锥体部分的高CD=3cm,求出这个陀螺的表面积(结果保留π).
25.列方程解应用题:如图,现有两条乡村公路AB、BC,AB长为1200米,BC长为1600米,一个人骑摩托车从A处以20m/s的速度匀速沿公路AB、BC向C处行驶;另一人骑自行车从B处以5m/s的速度从B向C行驶,并且两人同时出发.
(1)求经过多少秒摩托车追上自行车?
(2)求两人均在行驶途中时,经过多少秒两人在行进路线上相距150米?
26.计算:
(1)2×(﹣3)3﹣4×(﹣3);
(2)﹣22÷(﹣)×(﹣).
27.某水果销售店用1000元购进甲、乙两种水果共140千克,这两种水果的进价、售价如下表所示:
进价(元/千克)
售价(元/千克)
甲种水果
5
8
乙种水果
9
13
(1)这两种水果各购进多少千克?
(2)若该水果店把这两种水果全部售完,则可获利多少元.
28.计算:(﹣1)2﹣|﹣3|+(﹣5)÷(﹣).
29.在一张地图上量得上海与南京两地的距离为3.2厘米,又已知上海与南京、北京两地的实际距离分别约为300千米和1080千米,那么在这张地图上,上海与北京两地的距离为多少厘米?
参考答案与试题解析
一.选择题(共5小题,满分10分,每小题2分)
1.解:∵m在[5,15]内,n在[﹣30,﹣20]内,
∴5≤m≤15,﹣30≤n≤﹣20,
∴≤≤,即﹣6≤≤﹣,
∴的一切值中属于整数的有﹣2,﹣3,﹣4,﹣5,﹣6,共5个;
故选:A.
2.解:所得几何体的主视图的面积是2×3×3=18cm2.
故选:D.
3.解:A、因为:运货总吨数÷运货次数=每次运货吨数(一定),所以运货次数和运货总吨数成正比例,不合题意;
B、因为:运货总吨数÷每次运货吨数=运货次数(一定),所以每次运货的吨数和运货总吨数成正比例,不合题意;
C、因为:每次运货的吨数×运货的次数=运货总吨数(一定),所以每次运货的吨数和运货的次数成反比例,符合题意;
故选:C.
4.解:(1)若棱柱的底面边长相等,则它的各个侧面的面积相等,这种说法正确,
(2)正九棱柱有9条侧棱,9个侧面,侧面为长方形,这种说法正确,
(3)长方体、正方体都是棱柱,这种说法正确,
(4)三棱柱的侧面为三角形,这种说法不正确,侧面为矩形,
故选:D.
5.解:由题意可得,
第一次剩下:2021﹣2021×=,
第二次剩下:×(1﹣)=×=,
第三次剩下:×(1﹣)==,
…,
∴一直减到余下的,最后剩下的数是=1,
故选:B.
二.填空题(共7小题,满分14分,每小题2分)
6.解:∵向上挪动7cm,记为+7cm,
∴向下掉了3cm,可记作﹣3cm.
故答案为:﹣3.
7.解:连接AD,
∵△ABC是边长为2的等边三角形,
∴AD=2×=,
∴扇形的弧长为=π,
∴圆锥的底面圆的半径是π÷π÷2=.
故答案为:.
8.解:由题意可得,
佳佳和点点合买一单的花费为:(40+40×0.5)+16+15+14×2+9=128(元),
佳佳和点点合买一单的实际消费为:128﹣20+5=113(元);
佳佳买全需要的物品需要花费:40×0.5+16+14+9=59(元),
佳佳实际花费为:59﹣10+5=54(元),
点点买全需要的物品需要花费:40×0.5+15+14=49(元),
点点实际花费为:49﹣10+5=44(元),
若他们把想要的都买全,最少要花55+44=98(元);
当佳佳和点点各买一单,佳佳买一单点汉堡套餐、鸡翅、冰激凌、鸡块,共需20+16+15+14=65(元),实际消费为:65﹣15+5=55(元),点点买一单点汉堡套餐、冰淇淋、蔬菜沙拉,共需20+14+9=43(元),实际消费为43﹣10+5=38(元),若他们把想要的都买全,最少要花55+38=93(元);
∵113>98>93,
∴他们最少要花93元,
故答案为:93.
9.解::0.75
=×
=8:9.
故答案为:8:9.
10.解:第一个比的前项为:5×6=30或6÷5=1.2;
∴这个比例为:30:6=6:x或1.2:6=6:x,
30x=36或1.2x=36,
解得x=1.2或x=30.
故答案为:1.2或30.
11.解:两个外项互为倒数则乘积是1,
因为比例中内项之积等于外项之积,
所以两个内项的积也是1.
故答案为:1.
12.解:7纳米=0.000000007米=7×10﹣9米,
故答案为7×10﹣9.
三.填空题(共9小题,满分20分)
13.解:∵节约20元钱,记作“+20”元,
∴浪费15元钱,记作﹣15元.
故答案为:﹣15.
14.解:原式=9××
=12×
=16.
15.解:设小正方形的边长为xcm,则大正方形的边长为4+(5﹣x)厘米或(x+1+2)厘米,
根据题意得:4+(5﹣x)=(x+1+2),
解得:x=3,
∴4+(5﹣x)=6,
∴大正方形的面积为36平方厘米.
答:大正方形的面积为36平方厘米.
故答案为:36.
16.解:∵,
∴a=b,
则==.
故答案为:.
17.解:∵a
b=,
∴3
(﹣4
5)
=3
=3
=3
(﹣20)
=
=
=,
故答案为:.
18.解:三棱柱的两底展开是在矩形两端各有一个三角形,侧面展开是三个矩形,
所以不是三棱柱的展开图的是③.
故答案为:③.
19.解:设所想的数为x,
根据题意,得
(﹣3x+12)+x
=﹣x+2+x
=2.
故答案为2.
20.解:∵比例尺是1:5000,长方形地长300米,宽200米,
∴图上长为300×=0.06(米),
0.06米=6厘米,
图上宽为200×=0.04(米),
0.04米=4厘米,
∴图上面积为6×4=24(平方厘米).
故答案为:24.
21.解:∵五边形ABCDE与五边形A′B′C′D′E′是位似图形,
∴五边形ABCDE∽五边形A′B′C′D′E′.
∴五边形ABCDE与五边形A′B′C′D′E′的周长比等于相似比,面积比等于相似比的平方.
∵位似比为.若五边形ABCDE的面积为16cm2,周长为22cm,
∴五边形A′B′C′D′E′的面积为144cm2,周长为66cm.
故五边形A′B′C′D′E′的面积为144cm2,周长为66cm.
故答案为:144,66.
四.解答题(共2小题,满分24分,每小题12分)
22.解:(1)()×
=××
=3+4
=7;
(2)×
=×+×
=(+)×
=1×
=.
23.解:设这个数为x,根据题意可得:
x÷4﹣2=x+8,
解得:x=﹣120,
答:这个数是﹣120.
五.解答题(共6小题,满分32分)
24.解:根据题意,圆柱的底面积=π×42=16π,
圆柱的侧面积=2π×4×6=48π,
圆锥的母线长为=5,
所以圆锥的侧面积=×2π×4×5=20π,
所以这个陀螺的表面积=16π+48π+20π=84π(cm2).
25.解:(1)设经过x秒摩托车追上自行车,
20x=5x+1200,
解得x=80.
答:经过80秒摩托车追上自行车.
(2)(1200+1600)÷20=140(秒).
设经过y秒两人相距150米,
第一种情况:摩托车还差150米追上自行车时,
20y﹣1200=5y﹣150
解得y=70,符合题意.
第二种情况:摩托车超过自行车150米时,
20y=150+5y+1200
解得y=90,符合题意.
答:经过70秒或90秒两人在行进路线上相距150米.
26.解:(1)原式=2×(﹣27)+12
=﹣54+12
=﹣42;
(2)原式=﹣4÷×(﹣)
=﹣24×(﹣)
=15.
27.解:(1)设购进甲种水果x千克,则购进乙种水果(140﹣x)千克,根据题意得:5x+9(140﹣x)=1000,
解得:x=65,
∴140﹣x=75.
答:购进甲种水果65千克,乙种水果75千克;
(2)(8﹣5)×65+(13﹣9)×75=495(元)
答:利润为495元.
28.解:原式=1﹣3+3=1.
29.解:设在这张地图上,上海与北京两地的距离为x厘米.根据题意得到:.
解得x=11.52,
答:在这张地图上,上海与北京两地的距离为11.52厘米.
同课章节目录
