2020-2021学年人教五四新版七年级(下)期中数学复习试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年人教五四新版七年级(下)期中数学复习试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 311.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 00:00:00 | ||
图片预览



文档简介
2020-2021学年人教五四新版七年级(下)期中数学复习试卷
一.选择题(共10小题,满分50分,每小题5分)
1.下列方程组中,是二元一次方程组的是( )
A.
B.
C.
D.
2.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.3cm,4cm,8cm
B.8cm,7cm,15cm
C.13cm,12cm,20cm
D.5cm,5cm,11cm
3.若m>n,则下列不等式一定成立的是( )
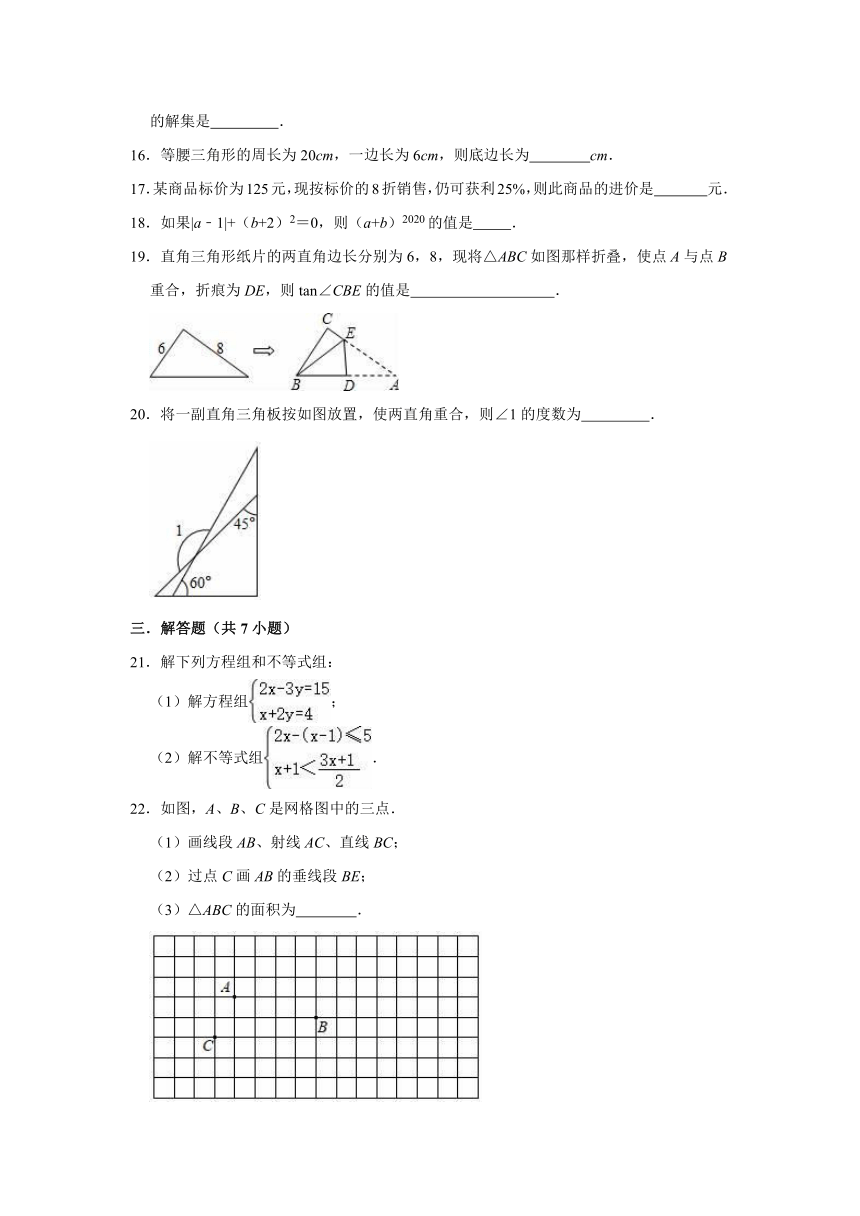
A.2m<3n
B.2+m>2+n
C.2﹣m>2﹣n
D.<
4.不等式2(3+x)≥8的解集在数轴上表示正确的是( )
A.
B.
C.
D.
5.下列说法中,正确的是( )
A.两点确定一条直线
B.顶点在圆上的角叫做圆心角
C.两条射线组成的图形叫做角
D.三角形不是多边形
6.为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是( )
A.两点之间,线段最短
B.垂线段最短
C.三角形具有稳定性
D.两直线平行,内错角相等
7.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
8.关于x,y的方程组(其中a,b是常数)的解为,则方程组的解为( )
A.
B.
C.
D.
9.某剧场为希望工程义演的文艺表演有60元和100元两种票价,某团体需购买140张,其中票价为100元的票数不少于票价为60元的票数的两倍,则购买这两种票最少共需要( )
A.12120元
B.12140元
C.12160元
D.12200元
10.工人师傅常用角尺平分一个任意角.作法如下:如图所示,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC即是∠AOB的平分线.这种作法的道理是( )
A.HL
B.SSS
C.SAS
D.ASA
二.填空题(共10小题,满分50分,每小题5分)
11.已知方程5x+3y=1,改写成用含x的式子表示y的形式
.
12.“x与3的和是非负数”用不等式表示为
.
13.已知一个正多边形的每个内角都是150°,则这个正多边形是正
边形.
14.点P(x﹣2,3+x)在第二象限,则x的取值范围是
.
15.若关于x的不等式ax<﹣bx+b(a,b≠0)的解集为x>,则关于x的不等式ax>2bx+b的解集是
.
16.等腰三角形的周长为20cm,一边长为6cm,则底边长为
cm.
17.某商品标价为125元,现按标价的8折销售,仍可获利25%,则此商品的进价是
元.
18.如果|a﹣1|+(b+2)2=0,则(a+b)2020的值是
.
19.直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是
.
20.将一副直角三角板按如图放置,使两直角重合,则∠1的度数为
.
三.解答题(共7小题)
21.解下列方程组和不等式组:
(1)解方程组;
(2)解不等式组.
22.如图,A、B、C是网格图中的三点.
(1)画线段AB、射线AC、直线BC;
(2)过点C画AB的垂线段BE;
(3)△ABC的面积为
.
23.已知不等式3(x﹣2)﹣5>6(x+1)﹣7的最大整数解是方程2x﹣mx=﹣10的解,求m的值.
24.如图,四边形ABCD的对角线AC、BD相交于点O,OA=OB,OC=OD.求证:
(1)AB∥CD;
(2)△ABC≌△BAD.
25.目前节能灯已基本普及,节能还环保,销量非常好,某商场计划购进甲、乙两种型号节能灯共1200只,这两种节能灯的进价、售价如表所示:
进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
(1)商场应如何进货,使进货款恰好为46000元?
(2)若商场销售完节能灯后获利不超过进货价的30%,至少购进甲种型号节能灯多少只?
26.在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图,当点D在BC延长线上移动时,若∠BAC=40°,则∠ACE=
,∠DCE=
,BC、DC、CE之间的数量关系为
;
(2)设∠BAC=α,∠DCE=β.
①当点D在BC延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B,C两点重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.
(3)当CE∥AB时,若△ABD中最小角为15°,试探究∠ACB的度数(直接写出结果,无需写出求解过程).
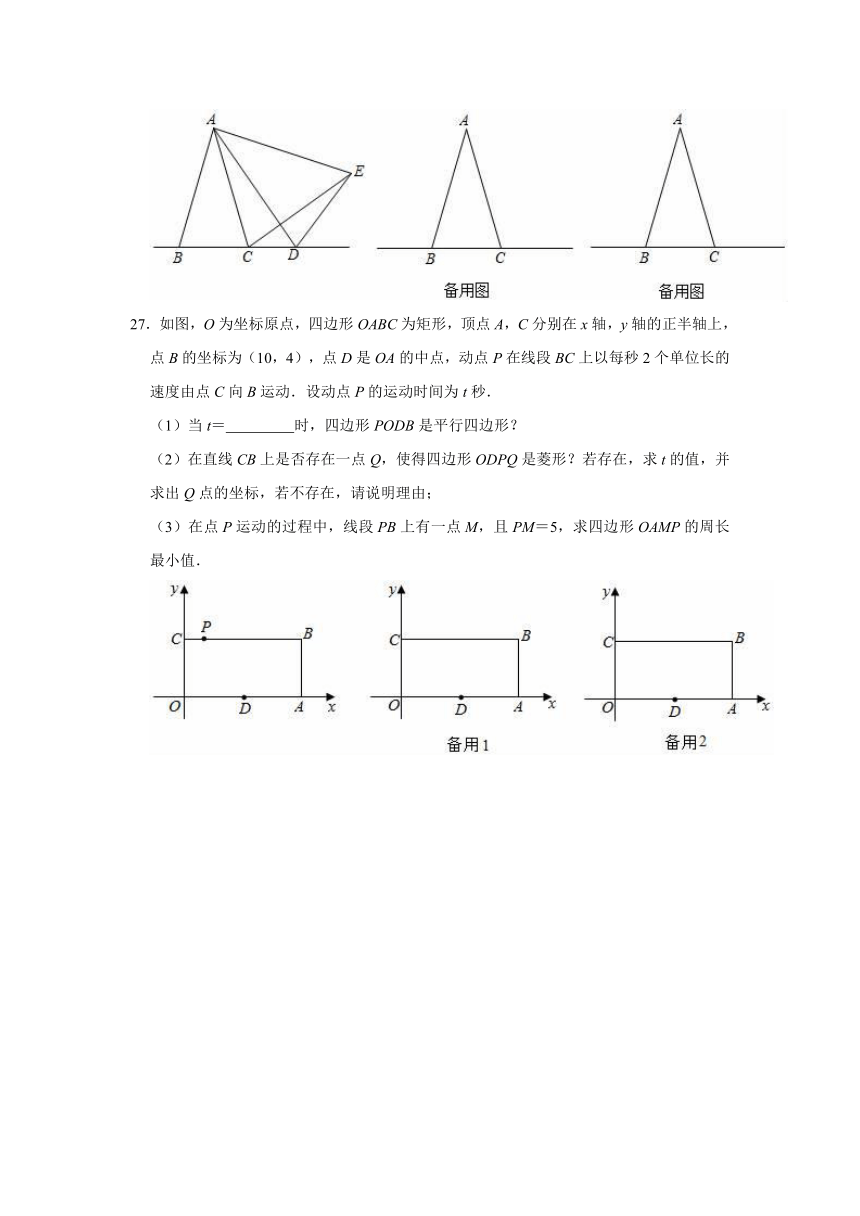
27.如图,O为坐标原点,四边形OABC为矩形,顶点A,C分别在x轴,y轴的正半轴上,点B的坐标为(10,4),点D是OA的中点,动点P在线段BC上以每秒2个单位长的速度由点C向B运动.设动点P的运动时间为t秒.
(1)当t=
时,四边形PODB是平行四边形?
(2)在直线CB上是否存在一点Q,使得四边形ODPQ是菱形?若存在,求t的值,并求出Q点的坐标,若不存在,请说明理由;
(3)在点P运动的过程中,线段PB上有一点M,且PM=5,求四边形OAMP的周长最小值.
参考答案与试题解析
一.选择题(共10小题,满分50分,每小题5分)
1.解:A、该方程组中含有3个未知数,属于三元一次方程组,故此选项错误;
B、该方程组中未知数的最高次数是2,属于二元二次方程组,故此选项错误;
C、该方程组中未知数的最高次数是2,属于二元二次方程组,故此选项错误;
D、该方程组符合二元一次方程组的定义,故此选项正确;
故选:D.
2.解:A、3+4<8,不能组成三角形;
B、8+7=15,不能组成三角形;
C、13+12>20,能够组成三角形;
D、5+5<11,不能组成三角形.
故选:C.
3.解:A、若m=3,n=﹣2,则2m>3n,故不符合题意.
B、若m>n,则2+m>2+n,故符合题意.
C、若m>n,则2﹣m<2﹣n,故不符合题意.
D、若m>n,则>,故不符合题意.
故选:B.
4.解:去括号,得6+2x≥8,
移项,得2x≥8﹣6,
合并同类项,得2x≥2,
两边都除以2,得x≥1,
故选:D.
5.解:A、根据直线的性质可知:两点确定一条直线,故本选项正确;
B、顶点在圆上的角叫圆心角,顶点在圆上的角角圆周角,故本选项错误;
C、两条射线若能组成角,则必须有公共端点,而如图所示图形则不是角.
,故本选项错误;
D、三角形有3条边组成,所以三角形是多边形,故本选项错误;
故选:A.
6.解:这样做的道理是三角形具有稳定性.
故选:C.
7.解:图甲不符合三角形全等的判定定理,即图甲和△ABC不全等;
图乙符合SAS定理,即图乙和△ABC全等;
图丙符合AAS定理,即图丙和△ABC全等;
故选:B.
8.解:由题意知,,
①+②,得:2x=7,x=3.5,
①﹣②,得:2y=﹣1,y=﹣0.5,
所以方程组的解为,
故选:C.
9.解:设票价为60元的票数为x张,票价为100元的票数为y张,故
可得:x≤
由题意可知:x,y为正整数,故x=46,y=94,
∴购买这两种票最少需要60×46+100×94=12160.
故选:C.
10.解:由图可知,CM=CN,又OM=ON,OC为公共边,
∴△COM≌△CON,
∴∠AOC=∠BOC,
即OC即是∠AOB的平分线.
故选:B.
二.填空题(共10小题,满分50分,每小题5分)
11.解:5x+3y=1,
3y=1﹣5x,
y=.
故答案为:y=.
12.解:由题意可得:x+3≥0.
故答案为:x+3≥0.
13.解:外角是:180°﹣150°=30°,
360°÷30°=12.
则这个正多边形是正十二边形.
故答案为:十二.
14.解:因为点P(x﹣2,3+x)在第二象限,
所以x﹣2<0,3+x>0,
解得﹣3<x<2.
故答案为﹣3<x<2.
15.解:ax<﹣bx+b,
(a+b)x<b,
∵关于x的不等式ax<﹣bx+b(a,b≠0)的解集为x>,
∴=,且a+b<0,
∴a=b<0,
∴ax>2bx+b变为﹣bx>b,
∴x>﹣1,
故答案为x>﹣1.
16.解:①6cm是底边时,腰长=(20﹣6)=7cm,
此时三角形的三边分别为7cm、7cm、6cm,
能组成三角形,
②6cm是腰长时,底边=20﹣6×2=8cm,
此时三角形的三边分别为6cm、6cm、8cm,
能组成三角形,
综上所述,底边长为6或8cm.
故答案为:6或8.
17.解:设此商品的进价为x元,
根据题意得:125×0.8﹣x=25%x,
解得:x=80.
故答案为:80.
18.解:∵|a﹣1|+(b+2)2=0,
∴a﹣1=0,b+2=0,
解得a=1,b=﹣2,
∴(a+b)2020=(1﹣2)2020=1.
故答案为:1.
19.解:根据题意,BE=AE.设BE=x,则CE=8﹣x.
在Rt△BCE中,x2=(8﹣x)2+62,
解得x=,故CE=8﹣=,
∴tan∠CBE==.
故答案为:.
20.解:如图,由题意知,∠CAD=60°,∠B=90°﹣45°=45°,
∴∠CAB=120°,
∴∠1=∠B+∠CAB=45°+120°=165°.
故答案为:165°.
三.解答题(共7小题)
21.解:(1),
①﹣②×2,得:﹣7y=7,
解得y=﹣1,
将y=﹣1代入②,得:x﹣2=4,
解得x=6,
所以方程组的解为;
(2)解不等式2x﹣(x﹣1)≤5,得:x≤4,
解不等式x+1<,得:x>1,
则不等式组的解集为1<x≤4.
22.解:(1)如图所示:线段AB、射线AC、直线BC,即为所求;
(2)如图所示:BE即为所求;
(3)△ABC的面积为:2×5﹣×1×2﹣×1×4﹣×1×5=4.5.
故答案为:4.5.
23.解:3(x﹣2)﹣5>6(x+1)﹣7,
3x﹣6﹣5>6x+6﹣7,
﹣3x>10,
∴x<﹣,
∴最大整数解为﹣4,
把x=﹣4代入2x﹣mx=﹣10,得:﹣8+4m=﹣10,
解得m=﹣.
24.(1)证明:∵OA=OB,OC=OD,
∴∠OAB=∠OBA,∠OCD=∠ODC,
∵∠COD=∠AOB,∠OAB+∠OBA+∠AOB=180°,∠OCD+∠ODC+∠COD=180°,
∴∠OAB=∠OBA=∠OCD=∠ODC,
即∠OAB=∠OCD,
∴AB∥CD;
(2)∵OA=OB,OC=OD,
∴AC=BD,
在△ABC和△BAD中,
,
∴△ABC≌△BAD(SAS).
25.解:(1)设购进甲型节能灯x只,乙型节能灯y只,
根据题意,得:,
解得:,
答:购进甲型节能灯400只,乙型节能灯800只,进货款恰好为46000元;
(2)设商场购进甲型节能灯a只,则购进乙型节能灯(1200﹣a)只,
由题意,得:(30﹣25)a+(60﹣45)(1200﹣a)≤[25a+45(1200﹣a)]×30%,
解得:a≥450.
答:至少购进甲种型号节能灯450只.
26.解:(1)如图1所示:∵∠DAE=∠BAC,
∴∠DAE+∠CAD=∠BAC+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠B=(180°﹣40°)=70°,BD=CE,
∴BC+DC=CE,
∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,
∴∠BAC=∠DCE,
∵∠BAC=40°,
∴∠DCE=40°,
故答案为:70°;40°;BC+DC=CE;
(2)①当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β,理由如下:
∵∠DAE=∠BAC,
∴∠DAE+∠CAD=∠BAC+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,,
∴△BAD≌△CAE(SAS),
∴∠B=∠ACE,
∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,
∴∠BAC=∠DCE,
∵∠BAC=α,∠DCE=β,
∴α=β;
②分三种情况:
(Ⅰ)当D在线段BC上时,α+β=180°,如图2所示,理由如下:
同理可证明:△ABD≌△ACE(SAS),
∴∠ADB=∠AEC,∠ABC=∠ACE,
∵∠ADC+∠ADB=180°,
∴∠ADC+∠AEC=180°,
∴∠DAE+∠DCE=180°,
∵∠BAC=∠DAE=α,∠DCE=β,
∴α+β=180°;
(Ⅱ)当点D在线段BC反向延长线上时,α=β,如图3所示,理由如下:
同理可证明:△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵∠ACE=∠ACD+∠DCE,∠ABD=∠ACD+∠BAC,
∴∠ACD+∠DCE=∠ACD+∠BAC,
∴∠BAC=∠DCE,
∵∠BAC=α,∠DCE=β,
∴α=β;
(Ⅲ)当点D在线段BC的延长线上时,如图1所示,α=β;
综上所述,当点D在BC上移动时,α=β或α+β=180°;
(3)∠ACB=60°,理由如下:
∵当点D在线段BC的延长线上或在线段BC反向延长线上移动时,α=β,
即∠BAC=∠DCE,
∵CE∥AB,
∴∠ABC=∠DCE,
∴∠ABC=∠BAC,
∵AB=AC,
∴∠ABC=∠ACB=∠BAC,
∴△ABC是等边三角形,
∴∠ACB=60°;
∵当D在线段BC上时,α+β=180°,
即∠BAC+∠DCE=180°,
∵CE∥AB,
∴∠ABC+∠DCE=180°,
∴∠ABC=∠BAC,
∵AB=AC,
∴∠ABC=∠ACB=∠BAC,
∴△ABC是等边三角形,
∴∠ACB=60°;
综上所述,当CE∥AB时,若△ABD中最小角为15°,∠ACB的度数为60°.
27.解:(1)∵四边形OABC为矩形,点B的坐标为(10,4),
∴BC=OA=10,AB=OC=4,
∵点D是OA的中点,
∴OD=OA=5,
由题意知,PC=2t,
∴BP=BC﹣PC=10﹣2t,
∵四边形PODB是平行四边形,
∴PB=OD=5,
∴10﹣2t=5,
∴t=2.5,
即当t=2.5s时,四边形PODB是平行四边形;
故答案为:2.5s;
(2)①当点Q在线段BC上时,如图1,
∵四边形ODPQ是菱形,
∴OQ=OD=5,
在Rt△OCQ中,,CP=3+5=8,
∴t=4,点Q的坐标为(3,4);
②当点Q在射线BC上时,如图2,
∵四边形ODPQ是菱形,
∴OQ=OD=5,
在Rt△OCQ中,,CP=5﹣3=2,
∴t=1,点Q的坐标为(﹣3,4);
(3)如图3,连接DM,
∵PM=OD=5,PM∥OD
∴四边形ODMP是平行四边形,
∴OP=DM
∴四边形OAMP的周长=OA+AM+MP+PO=15+AM+PO=15+AM+DM
作点A关于直线BC的对称点A′,连接A′M,A′D,
∵AM=A′M
∴四边形OAMP的周长=15+A′M+DM,
所以,当点A′,M,D三点在同一直线上时,四边形OAMP的周长最小,
在Rt△A′DA中,,
所以四边形OAMP的周长最小值为.
一.选择题(共10小题,满分50分,每小题5分)
1.下列方程组中,是二元一次方程组的是( )
A.
B.
C.
D.
2.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.3cm,4cm,8cm
B.8cm,7cm,15cm
C.13cm,12cm,20cm
D.5cm,5cm,11cm
3.若m>n,则下列不等式一定成立的是( )
A.2m<3n
B.2+m>2+n
C.2﹣m>2﹣n
D.<
4.不等式2(3+x)≥8的解集在数轴上表示正确的是( )
A.
B.
C.
D.
5.下列说法中,正确的是( )
A.两点确定一条直线
B.顶点在圆上的角叫做圆心角
C.两条射线组成的图形叫做角
D.三角形不是多边形
6.为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是( )
A.两点之间,线段最短
B.垂线段最短
C.三角形具有稳定性
D.两直线平行,内错角相等
7.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
8.关于x,y的方程组(其中a,b是常数)的解为,则方程组的解为( )
A.
B.
C.
D.
9.某剧场为希望工程义演的文艺表演有60元和100元两种票价,某团体需购买140张,其中票价为100元的票数不少于票价为60元的票数的两倍,则购买这两种票最少共需要( )
A.12120元
B.12140元
C.12160元
D.12200元
10.工人师傅常用角尺平分一个任意角.作法如下:如图所示,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC即是∠AOB的平分线.这种作法的道理是( )
A.HL
B.SSS
C.SAS
D.ASA
二.填空题(共10小题,满分50分,每小题5分)
11.已知方程5x+3y=1,改写成用含x的式子表示y的形式
.
12.“x与3的和是非负数”用不等式表示为
.
13.已知一个正多边形的每个内角都是150°,则这个正多边形是正
边形.
14.点P(x﹣2,3+x)在第二象限,则x的取值范围是
.
15.若关于x的不等式ax<﹣bx+b(a,b≠0)的解集为x>,则关于x的不等式ax>2bx+b的解集是
.
16.等腰三角形的周长为20cm,一边长为6cm,则底边长为
cm.
17.某商品标价为125元,现按标价的8折销售,仍可获利25%,则此商品的进价是
元.
18.如果|a﹣1|+(b+2)2=0,则(a+b)2020的值是
.
19.直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是
.
20.将一副直角三角板按如图放置,使两直角重合,则∠1的度数为
.
三.解答题(共7小题)
21.解下列方程组和不等式组:
(1)解方程组;
(2)解不等式组.
22.如图,A、B、C是网格图中的三点.
(1)画线段AB、射线AC、直线BC;
(2)过点C画AB的垂线段BE;
(3)△ABC的面积为
.
23.已知不等式3(x﹣2)﹣5>6(x+1)﹣7的最大整数解是方程2x﹣mx=﹣10的解,求m的值.
24.如图,四边形ABCD的对角线AC、BD相交于点O,OA=OB,OC=OD.求证:
(1)AB∥CD;
(2)△ABC≌△BAD.
25.目前节能灯已基本普及,节能还环保,销量非常好,某商场计划购进甲、乙两种型号节能灯共1200只,这两种节能灯的进价、售价如表所示:
进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
(1)商场应如何进货,使进货款恰好为46000元?
(2)若商场销售完节能灯后获利不超过进货价的30%,至少购进甲种型号节能灯多少只?
26.在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图,当点D在BC延长线上移动时,若∠BAC=40°,则∠ACE=
,∠DCE=
,BC、DC、CE之间的数量关系为
;
(2)设∠BAC=α,∠DCE=β.
①当点D在BC延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B,C两点重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.
(3)当CE∥AB时,若△ABD中最小角为15°,试探究∠ACB的度数(直接写出结果,无需写出求解过程).
27.如图,O为坐标原点,四边形OABC为矩形,顶点A,C分别在x轴,y轴的正半轴上,点B的坐标为(10,4),点D是OA的中点,动点P在线段BC上以每秒2个单位长的速度由点C向B运动.设动点P的运动时间为t秒.
(1)当t=
时,四边形PODB是平行四边形?
(2)在直线CB上是否存在一点Q,使得四边形ODPQ是菱形?若存在,求t的值,并求出Q点的坐标,若不存在,请说明理由;
(3)在点P运动的过程中,线段PB上有一点M,且PM=5,求四边形OAMP的周长最小值.
参考答案与试题解析
一.选择题(共10小题,满分50分,每小题5分)
1.解:A、该方程组中含有3个未知数,属于三元一次方程组,故此选项错误;
B、该方程组中未知数的最高次数是2,属于二元二次方程组,故此选项错误;
C、该方程组中未知数的最高次数是2,属于二元二次方程组,故此选项错误;
D、该方程组符合二元一次方程组的定义,故此选项正确;
故选:D.
2.解:A、3+4<8,不能组成三角形;
B、8+7=15,不能组成三角形;
C、13+12>20,能够组成三角形;
D、5+5<11,不能组成三角形.
故选:C.
3.解:A、若m=3,n=﹣2,则2m>3n,故不符合题意.
B、若m>n,则2+m>2+n,故符合题意.
C、若m>n,则2﹣m<2﹣n,故不符合题意.
D、若m>n,则>,故不符合题意.
故选:B.
4.解:去括号,得6+2x≥8,
移项,得2x≥8﹣6,
合并同类项,得2x≥2,
两边都除以2,得x≥1,
故选:D.
5.解:A、根据直线的性质可知:两点确定一条直线,故本选项正确;
B、顶点在圆上的角叫圆心角,顶点在圆上的角角圆周角,故本选项错误;
C、两条射线若能组成角,则必须有公共端点,而如图所示图形则不是角.
,故本选项错误;
D、三角形有3条边组成,所以三角形是多边形,故本选项错误;
故选:A.
6.解:这样做的道理是三角形具有稳定性.
故选:C.
7.解:图甲不符合三角形全等的判定定理,即图甲和△ABC不全等;
图乙符合SAS定理,即图乙和△ABC全等;
图丙符合AAS定理,即图丙和△ABC全等;
故选:B.
8.解:由题意知,,
①+②,得:2x=7,x=3.5,
①﹣②,得:2y=﹣1,y=﹣0.5,
所以方程组的解为,
故选:C.
9.解:设票价为60元的票数为x张,票价为100元的票数为y张,故
可得:x≤
由题意可知:x,y为正整数,故x=46,y=94,
∴购买这两种票最少需要60×46+100×94=12160.
故选:C.
10.解:由图可知,CM=CN,又OM=ON,OC为公共边,
∴△COM≌△CON,
∴∠AOC=∠BOC,
即OC即是∠AOB的平分线.
故选:B.
二.填空题(共10小题,满分50分,每小题5分)
11.解:5x+3y=1,
3y=1﹣5x,
y=.
故答案为:y=.
12.解:由题意可得:x+3≥0.
故答案为:x+3≥0.
13.解:外角是:180°﹣150°=30°,
360°÷30°=12.
则这个正多边形是正十二边形.
故答案为:十二.
14.解:因为点P(x﹣2,3+x)在第二象限,
所以x﹣2<0,3+x>0,
解得﹣3<x<2.
故答案为﹣3<x<2.
15.解:ax<﹣bx+b,
(a+b)x<b,
∵关于x的不等式ax<﹣bx+b(a,b≠0)的解集为x>,
∴=,且a+b<0,
∴a=b<0,
∴ax>2bx+b变为﹣bx>b,
∴x>﹣1,
故答案为x>﹣1.
16.解:①6cm是底边时,腰长=(20﹣6)=7cm,
此时三角形的三边分别为7cm、7cm、6cm,
能组成三角形,
②6cm是腰长时,底边=20﹣6×2=8cm,
此时三角形的三边分别为6cm、6cm、8cm,
能组成三角形,
综上所述,底边长为6或8cm.
故答案为:6或8.
17.解:设此商品的进价为x元,
根据题意得:125×0.8﹣x=25%x,
解得:x=80.
故答案为:80.
18.解:∵|a﹣1|+(b+2)2=0,
∴a﹣1=0,b+2=0,
解得a=1,b=﹣2,
∴(a+b)2020=(1﹣2)2020=1.
故答案为:1.
19.解:根据题意,BE=AE.设BE=x,则CE=8﹣x.
在Rt△BCE中,x2=(8﹣x)2+62,
解得x=,故CE=8﹣=,
∴tan∠CBE==.
故答案为:.
20.解:如图,由题意知,∠CAD=60°,∠B=90°﹣45°=45°,
∴∠CAB=120°,
∴∠1=∠B+∠CAB=45°+120°=165°.
故答案为:165°.
三.解答题(共7小题)
21.解:(1),
①﹣②×2,得:﹣7y=7,
解得y=﹣1,
将y=﹣1代入②,得:x﹣2=4,
解得x=6,
所以方程组的解为;
(2)解不等式2x﹣(x﹣1)≤5,得:x≤4,
解不等式x+1<,得:x>1,
则不等式组的解集为1<x≤4.
22.解:(1)如图所示:线段AB、射线AC、直线BC,即为所求;
(2)如图所示:BE即为所求;
(3)△ABC的面积为:2×5﹣×1×2﹣×1×4﹣×1×5=4.5.
故答案为:4.5.
23.解:3(x﹣2)﹣5>6(x+1)﹣7,
3x﹣6﹣5>6x+6﹣7,
﹣3x>10,
∴x<﹣,
∴最大整数解为﹣4,
把x=﹣4代入2x﹣mx=﹣10,得:﹣8+4m=﹣10,
解得m=﹣.
24.(1)证明:∵OA=OB,OC=OD,
∴∠OAB=∠OBA,∠OCD=∠ODC,
∵∠COD=∠AOB,∠OAB+∠OBA+∠AOB=180°,∠OCD+∠ODC+∠COD=180°,
∴∠OAB=∠OBA=∠OCD=∠ODC,
即∠OAB=∠OCD,
∴AB∥CD;
(2)∵OA=OB,OC=OD,
∴AC=BD,
在△ABC和△BAD中,
,
∴△ABC≌△BAD(SAS).
25.解:(1)设购进甲型节能灯x只,乙型节能灯y只,
根据题意,得:,
解得:,
答:购进甲型节能灯400只,乙型节能灯800只,进货款恰好为46000元;
(2)设商场购进甲型节能灯a只,则购进乙型节能灯(1200﹣a)只,
由题意,得:(30﹣25)a+(60﹣45)(1200﹣a)≤[25a+45(1200﹣a)]×30%,
解得:a≥450.
答:至少购进甲种型号节能灯450只.
26.解:(1)如图1所示:∵∠DAE=∠BAC,
∴∠DAE+∠CAD=∠BAC+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠B=(180°﹣40°)=70°,BD=CE,
∴BC+DC=CE,
∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,
∴∠BAC=∠DCE,
∵∠BAC=40°,
∴∠DCE=40°,
故答案为:70°;40°;BC+DC=CE;
(2)①当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β,理由如下:
∵∠DAE=∠BAC,
∴∠DAE+∠CAD=∠BAC+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,,
∴△BAD≌△CAE(SAS),
∴∠B=∠ACE,
∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,
∴∠BAC=∠DCE,
∵∠BAC=α,∠DCE=β,
∴α=β;
②分三种情况:
(Ⅰ)当D在线段BC上时,α+β=180°,如图2所示,理由如下:
同理可证明:△ABD≌△ACE(SAS),
∴∠ADB=∠AEC,∠ABC=∠ACE,
∵∠ADC+∠ADB=180°,
∴∠ADC+∠AEC=180°,
∴∠DAE+∠DCE=180°,
∵∠BAC=∠DAE=α,∠DCE=β,
∴α+β=180°;
(Ⅱ)当点D在线段BC反向延长线上时,α=β,如图3所示,理由如下:
同理可证明:△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵∠ACE=∠ACD+∠DCE,∠ABD=∠ACD+∠BAC,
∴∠ACD+∠DCE=∠ACD+∠BAC,
∴∠BAC=∠DCE,
∵∠BAC=α,∠DCE=β,
∴α=β;
(Ⅲ)当点D在线段BC的延长线上时,如图1所示,α=β;
综上所述,当点D在BC上移动时,α=β或α+β=180°;
(3)∠ACB=60°,理由如下:
∵当点D在线段BC的延长线上或在线段BC反向延长线上移动时,α=β,
即∠BAC=∠DCE,
∵CE∥AB,
∴∠ABC=∠DCE,
∴∠ABC=∠BAC,
∵AB=AC,
∴∠ABC=∠ACB=∠BAC,
∴△ABC是等边三角形,
∴∠ACB=60°;
∵当D在线段BC上时,α+β=180°,
即∠BAC+∠DCE=180°,
∵CE∥AB,
∴∠ABC+∠DCE=180°,
∴∠ABC=∠BAC,
∵AB=AC,
∴∠ABC=∠ACB=∠BAC,
∴△ABC是等边三角形,
∴∠ACB=60°;
综上所述,当CE∥AB时,若△ABD中最小角为15°,∠ACB的度数为60°.
27.解:(1)∵四边形OABC为矩形,点B的坐标为(10,4),
∴BC=OA=10,AB=OC=4,
∵点D是OA的中点,
∴OD=OA=5,
由题意知,PC=2t,
∴BP=BC﹣PC=10﹣2t,
∵四边形PODB是平行四边形,
∴PB=OD=5,
∴10﹣2t=5,
∴t=2.5,
即当t=2.5s时,四边形PODB是平行四边形;
故答案为:2.5s;
(2)①当点Q在线段BC上时,如图1,
∵四边形ODPQ是菱形,
∴OQ=OD=5,
在Rt△OCQ中,,CP=3+5=8,
∴t=4,点Q的坐标为(3,4);
②当点Q在射线BC上时,如图2,
∵四边形ODPQ是菱形,
∴OQ=OD=5,
在Rt△OCQ中,,CP=5﹣3=2,
∴t=1,点Q的坐标为(﹣3,4);
(3)如图3,连接DM,
∵PM=OD=5,PM∥OD
∴四边形ODMP是平行四边形,
∴OP=DM
∴四边形OAMP的周长=OA+AM+MP+PO=15+AM+PO=15+AM+DM
作点A关于直线BC的对称点A′,连接A′M,A′D,
∵AM=A′M
∴四边形OAMP的周长=15+A′M+DM,
所以,当点A′,M,D三点在同一直线上时,四边形OAMP的周长最小,
在Rt△A′DA中,,
所以四边形OAMP的周长最小值为.
同课章节目录
