2020-2021学年高中数学人教A版必修2第二章2.3.2 平面与平面垂直的判定教学课件(共26张PPT)
文档属性
| 名称 | 2020-2021学年高中数学人教A版必修2第二章2.3.2 平面与平面垂直的判定教学课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-30 22:31:16 | ||
图片预览



文档简介
(共26张PPT)
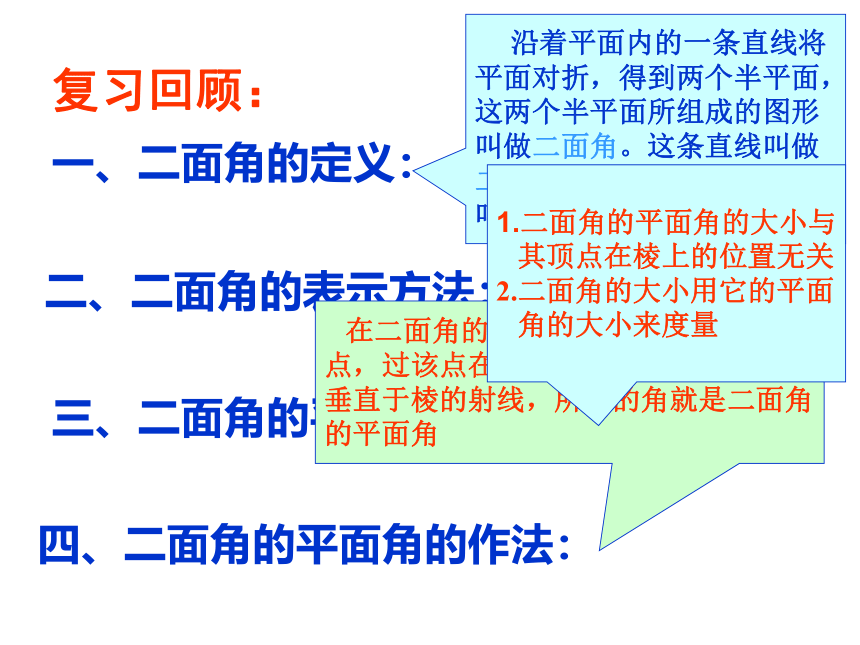
一、二面角的定义:
二、二面角的表示方法:
三、二面角的平面角的特点:
四、二面角的平面角的作法:
二
面
角
?-AB-
?
二
面
角
?-
l-
?
在二面角的棱上任取一点作为角的顶
点,过该点在二面角的两个面内分别作
垂直于棱的射线,所成的角就是二面角
的平面角
沿着平面内的一条直线将
平面对折,得到两个半平面,
这两个半平面所组成的图形
叫做二面角。这条直线叫做
二面角的棱。这两个半平面
叫做二面角的面。
1.二面角的平面角的大小与
其顶点在棱上的位置无关
2.二面角的大小用它的平面
角的大小来度量
复习回顾:
建筑工人砌墙时,常用一端系有铅锤的线来检查所砌的墙面是否和地面垂直,如果系有铅锤的线和墙面紧贴,那么所砌的墙与地面垂直.这是为什么呢?
情景引入
学习新知
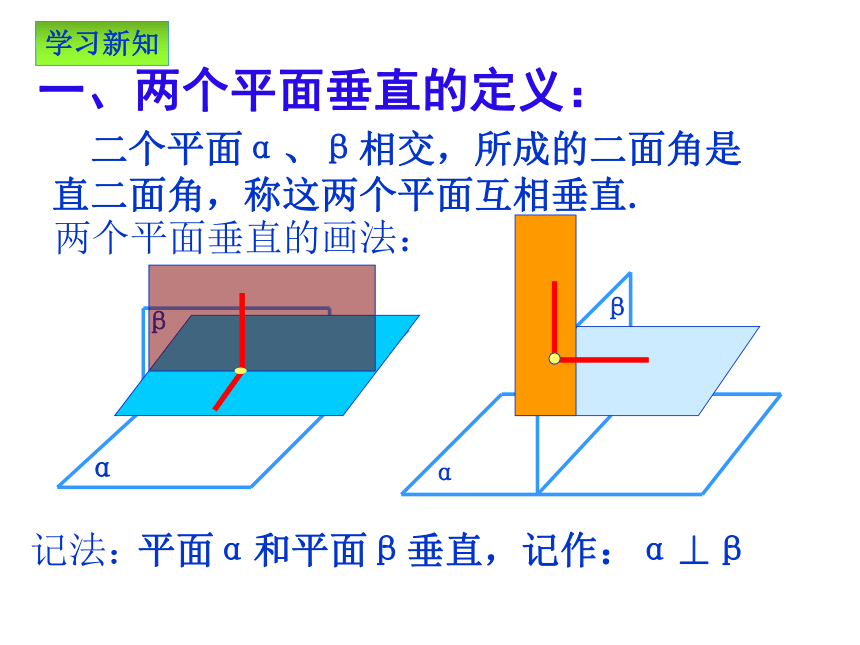
一、两个平面垂直的定义:
二个平面α、β相交,所成的二面角是
直二面角,称这两个平面互相垂直.
两个平面垂直的画法:
记法:
平面α和平面β垂直,记作:α⊥β
α
β
α
β
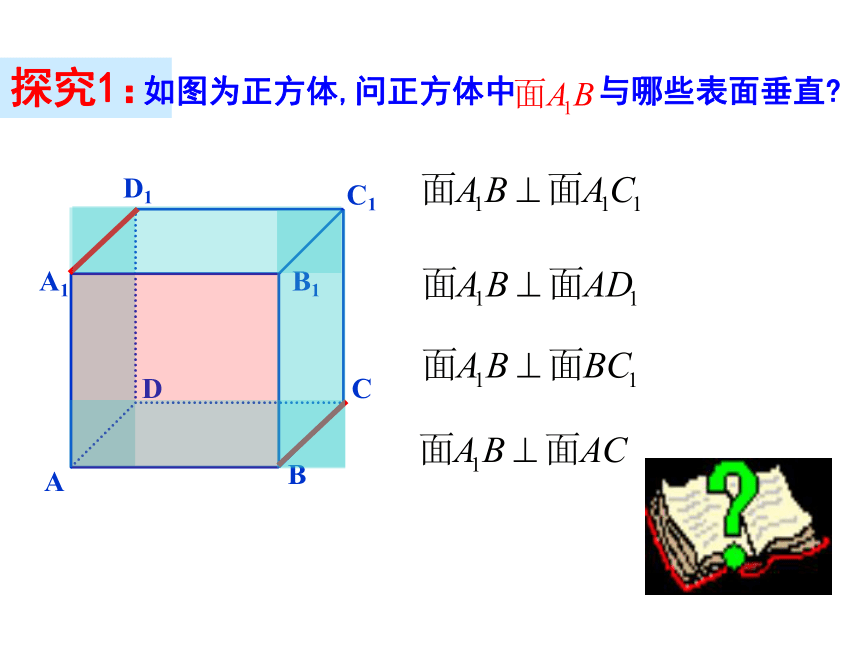
探究1:
A
C
B
D
A1
C1
B1
D1
如图为正方体,问正方体中
与哪些表面垂直?
(1)你能举出一些平面与平面垂直的实例吗?
(2)除了定义之外,如何判定两个平面互相垂直呢?
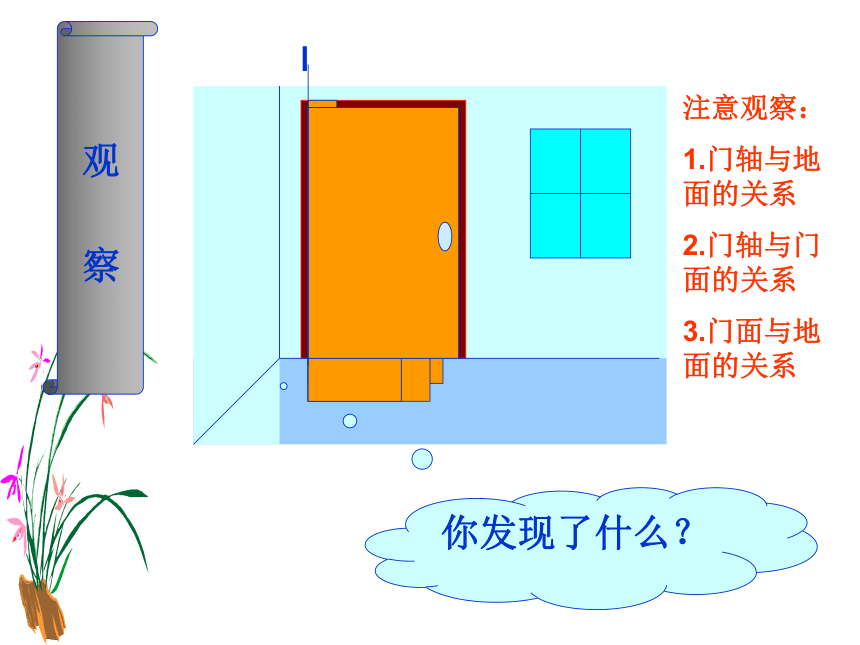
你发现了什么?
观
察
注意观察:
1.门轴与地面的关系
2.门轴与门面的关系
3.门面与地面的关系
ι
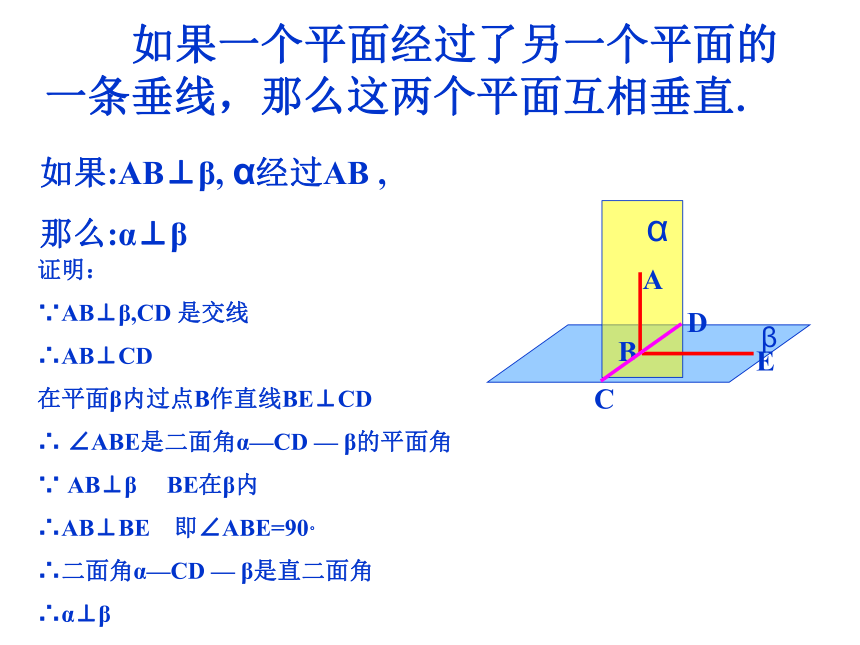
如果:AB⊥β,
α经过AB
,
那么:α⊥β
证明:
∵AB⊥β,CD
是交线
∴AB⊥CD
在平面β内过点B作直线BE⊥CD
∴
∠ABE是二面角α—CD
—
β的平面角
∵
AB⊥β
BE在β内
∴AB⊥BE
即∠ABE=90。
∴二面角α—CD
—
β是直二面角
∴α⊥β
如果一个平面经过了另一个平面的一条垂线,那么这两个平面互相垂直.
A
B
E
D
C
β
α
线线垂直
线面垂直
面面垂直
如果一个平面经过了另一个平面的一条垂线,那么这两个平面互相垂直.
α
β
A
B
简记:线面垂直,则面面垂直
符号:AB⊥α,
β经过AB,
则α⊥β
证明两个平面垂直有那些方法?
1.定义法
2.两平面垂直的判定定理
二、两个平面垂直的判定定理:
建筑工人砌墙时,
如何使所砌的墙和水平面垂直?
应
用
探究新知
教室的黑板所在平面与地面或桌面是什么关系?你能在黑板上画一条直线与地面或桌面垂直吗?
[探索研究
]:
如果两个平面互相垂直,那么在第一个平面内垂直于交线的直线,是否垂直于第二个平面呢?用实例来说明。
E
三、定理(面面垂直性质定理)
如果两个平面互相垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面。
设β⊥α,
AB为平面β内的一条直线,且AB
⊥CD,则AB⊥α。
简记:
面面垂直,则线面垂直
例
如图所示,直二面角α―l―β的棱l上有
A、B两个点,在α内过
A
作AC⊥
l,在β内过
B
作BD⊥
l。已知AC=6
cm,BD=24
cm,AB=8
cm,求CD的长。
6cm
24cm
8cm
课堂练习:
1.如果平面α内有一条直线垂直于平面β内的一条
直线,则α⊥β.(
)
3.
如果平面α内的一条直线垂直于平面β内的两条
相交直线,
则α⊥β.(
)
一、判断:
×
×
4.若a⊥α,a在β内,则α⊥β.(
)
√
2.如果平面α内有一条直线垂直于平面β内的两条
直线,则α⊥β.(
)
√
1.过平面α的一条垂线可作_____个平面
与平面α垂直.
2.过一点可作_____个平面与已知平面垂
直.
二、填空题:
3.过平面α的一条斜线,可作____个平
面与平面α垂直.
4.过平面α的一条平行线可作____个平
面与α垂直.
一
无数
无数
一
1.面面垂直的定义:
直二面角
面面垂直.
四、小结
2.面面垂直的判定定理:
线面垂直,则面面垂直.
3.面面垂直的性质定理:
面面垂直,则线面垂直.
概念巩固
判断下列命题的真假
1.若α⊥β,那么α内的所有直线都垂直于β。
2.两平面互相垂直,分别在这两平面内的两直线互相垂直。
3.两平面互相垂直,分别在两平面内且互相垂直的两直线一定分别与另一个平面垂直。
4.两平面互相垂直,过一平面内的任一点在该平面内作交线的垂线,则此直线必垂直与另一个平面。
×
×
×
√
请问哪些平面是互相垂直的,为什么?
探究2:
A
B
C
D
由面面垂直性质定理,可得两个推论:
推论1
如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线,在第一个平面内。
α⊥β,A在β内,AB⊥α,则AB在β内
推论2
如果两个相交平面都和第三个平面垂直,那么它们的交线也和第三个平面垂直。
α⊥γ,β
⊥γ
,
α和
β的交线为l,则l⊥γ
1.检查工件的相邻两个面是否
垂直时,只要将角尺的一边紧靠在
工件的一个面上,另一边在工件的
另一个面上转动一下,观察尺边是
否和该面密合就可以了为什么?
如果不转动呢?
2.二面角α-l-β为30°,α内有一点A到β的距离AB为10cm,求点A到棱l的距离。
[总结提炼]
☆
已知面面垂直易找面的垂线,且在某一个平面内
☆
解题过程中应注意充分领悟、应用
☆
证明面面垂直要从寻找面的垂线入手
☆
理解面面垂直的判定与性质都要依赖面面垂直的定义
☆
定义面面垂直是在建立在二面角的定义的基础上的
探究二:(以小组为单位完成)
1.教室的门转到任何位置时,门所在平面与地面有怎样的位置关系?为什么?
2.打开的书立在桌面上,各页所在的平面与桌面有怎样的位置关系?为什么?
一、二面角的定义:
二、二面角的表示方法:
三、二面角的平面角的特点:
四、二面角的平面角的作法:
二
面
角
?-AB-
?
二
面
角
?-
l-
?
在二面角的棱上任取一点作为角的顶
点,过该点在二面角的两个面内分别作
垂直于棱的射线,所成的角就是二面角
的平面角
沿着平面内的一条直线将
平面对折,得到两个半平面,
这两个半平面所组成的图形
叫做二面角。这条直线叫做
二面角的棱。这两个半平面
叫做二面角的面。
1.二面角的平面角的大小与
其顶点在棱上的位置无关
2.二面角的大小用它的平面
角的大小来度量
复习回顾:
建筑工人砌墙时,常用一端系有铅锤的线来检查所砌的墙面是否和地面垂直,如果系有铅锤的线和墙面紧贴,那么所砌的墙与地面垂直.这是为什么呢?
情景引入
学习新知
一、两个平面垂直的定义:
二个平面α、β相交,所成的二面角是
直二面角,称这两个平面互相垂直.
两个平面垂直的画法:
记法:
平面α和平面β垂直,记作:α⊥β
α
β
α
β
探究1:
A
C
B
D
A1
C1
B1
D1
如图为正方体,问正方体中
与哪些表面垂直?
(1)你能举出一些平面与平面垂直的实例吗?
(2)除了定义之外,如何判定两个平面互相垂直呢?
你发现了什么?
观
察
注意观察:
1.门轴与地面的关系
2.门轴与门面的关系
3.门面与地面的关系
ι
如果:AB⊥β,
α经过AB
,
那么:α⊥β
证明:
∵AB⊥β,CD
是交线
∴AB⊥CD
在平面β内过点B作直线BE⊥CD
∴
∠ABE是二面角α—CD
—
β的平面角
∵
AB⊥β
BE在β内
∴AB⊥BE
即∠ABE=90。
∴二面角α—CD
—
β是直二面角
∴α⊥β
如果一个平面经过了另一个平面的一条垂线,那么这两个平面互相垂直.
A
B
E
D
C
β
α
线线垂直
线面垂直
面面垂直
如果一个平面经过了另一个平面的一条垂线,那么这两个平面互相垂直.
α
β
A
B
简记:线面垂直,则面面垂直
符号:AB⊥α,
β经过AB,
则α⊥β
证明两个平面垂直有那些方法?
1.定义法
2.两平面垂直的判定定理
二、两个平面垂直的判定定理:
建筑工人砌墙时,
如何使所砌的墙和水平面垂直?
应
用
探究新知
教室的黑板所在平面与地面或桌面是什么关系?你能在黑板上画一条直线与地面或桌面垂直吗?
[探索研究
]:
如果两个平面互相垂直,那么在第一个平面内垂直于交线的直线,是否垂直于第二个平面呢?用实例来说明。
E
三、定理(面面垂直性质定理)
如果两个平面互相垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面。
设β⊥α,
AB为平面β内的一条直线,且AB
⊥CD,则AB⊥α。
简记:
面面垂直,则线面垂直
例
如图所示,直二面角α―l―β的棱l上有
A、B两个点,在α内过
A
作AC⊥
l,在β内过
B
作BD⊥
l。已知AC=6
cm,BD=24
cm,AB=8
cm,求CD的长。
6cm
24cm
8cm
课堂练习:
1.如果平面α内有一条直线垂直于平面β内的一条
直线,则α⊥β.(
)
3.
如果平面α内的一条直线垂直于平面β内的两条
相交直线,
则α⊥β.(
)
一、判断:
×
×
4.若a⊥α,a在β内,则α⊥β.(
)
√
2.如果平面α内有一条直线垂直于平面β内的两条
直线,则α⊥β.(
)
√
1.过平面α的一条垂线可作_____个平面
与平面α垂直.
2.过一点可作_____个平面与已知平面垂
直.
二、填空题:
3.过平面α的一条斜线,可作____个平
面与平面α垂直.
4.过平面α的一条平行线可作____个平
面与α垂直.
一
无数
无数
一
1.面面垂直的定义:
直二面角
面面垂直.
四、小结
2.面面垂直的判定定理:
线面垂直,则面面垂直.
3.面面垂直的性质定理:
面面垂直,则线面垂直.
概念巩固
判断下列命题的真假
1.若α⊥β,那么α内的所有直线都垂直于β。
2.两平面互相垂直,分别在这两平面内的两直线互相垂直。
3.两平面互相垂直,分别在两平面内且互相垂直的两直线一定分别与另一个平面垂直。
4.两平面互相垂直,过一平面内的任一点在该平面内作交线的垂线,则此直线必垂直与另一个平面。
×
×
×
√
请问哪些平面是互相垂直的,为什么?
探究2:
A
B
C
D
由面面垂直性质定理,可得两个推论:
推论1
如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线,在第一个平面内。
α⊥β,A在β内,AB⊥α,则AB在β内
推论2
如果两个相交平面都和第三个平面垂直,那么它们的交线也和第三个平面垂直。
α⊥γ,β
⊥γ
,
α和
β的交线为l,则l⊥γ
1.检查工件的相邻两个面是否
垂直时,只要将角尺的一边紧靠在
工件的一个面上,另一边在工件的
另一个面上转动一下,观察尺边是
否和该面密合就可以了为什么?
如果不转动呢?
2.二面角α-l-β为30°,α内有一点A到β的距离AB为10cm,求点A到棱l的距离。
[总结提炼]
☆
已知面面垂直易找面的垂线,且在某一个平面内
☆
解题过程中应注意充分领悟、应用
☆
证明面面垂直要从寻找面的垂线入手
☆
理解面面垂直的判定与性质都要依赖面面垂直的定义
☆
定义面面垂直是在建立在二面角的定义的基础上的
探究二:(以小组为单位完成)
1.教室的门转到任何位置时,门所在平面与地面有怎样的位置关系?为什么?
2.打开的书立在桌面上,各页所在的平面与桌面有怎样的位置关系?为什么?
