4.2 一元一次方程的解法课件

(共79张PPT)
一元一次方程的解法
本节内容
4.2
1. 如果 七年级(1)班的学生人数=八年级(2)班的学生人数，
现在每班增加2名学生，那么七年级(1)班与八班级(2)班的
学生人数还相等吗？
相 等
说一说
如果每班减少3名学生，那么这两个班的学生人数还相等吗？
相 等
2. 如果 甲筐米的重量=乙筐米的重量，
现在把甲、乙两筐的米分别倒出一半，那么甲、乙两
筐剩下的米的重量相等吗？
相 等
等式性质1 等式两边都加上（减去）同一个数（或同一个式），所得结果仍是等式.
结论
即，如果a = b，那么
a
± c
=
b
± c
结论
等式性质2 等式两边都乘（或除以）同一个数（或同一个式）（除数或除式不能为0），所得结果仍是等式.
即，如果a = b，那么
a
c
=
b
c
a
（d ≠ 0）
d
=
b
d
动脑筋
（我国古代数学问题）用绳子量井深，把绳子3折来量，井外余绳子4尺；把绳子4折来量，井外余绳子1尺.于是量井人说：“我知道这口井有多深了.”
你能算出这口井的深度吗？
分析：将绳子3折量井，绳长怎样表示呢？
3×(井深+4)尺.
那么将绳子4折量井，绳长又怎样表示呢？
4×(井深+1)尺.
因为绳子的长度没有变化，所以有等量关系：
4(井深+1)=3(井深+4).
设井深为x尺，根据题意，
得 4(x+1)=3(x+4)，
即 4x+4=3x+12. ①
如何求出方程①的解呢？
根据等式性质1，方程4x+4=3x+12可以用下面的方法来解.
在方程两边同时减去3x，得
4x+4-3x=3x+12-3x.
化简，得 x+4=12.
再在方程两边同时减去4，得
x+4-4=12-4.
化简，得x=8.
检验：把x=8代入方程①的左边和右边，得
左边=4×8+4=36，右边=3×8+12=36，
左边=右边.
所以x=8是原方程4x+4=3x+12的解.
答：这口井深8尺.
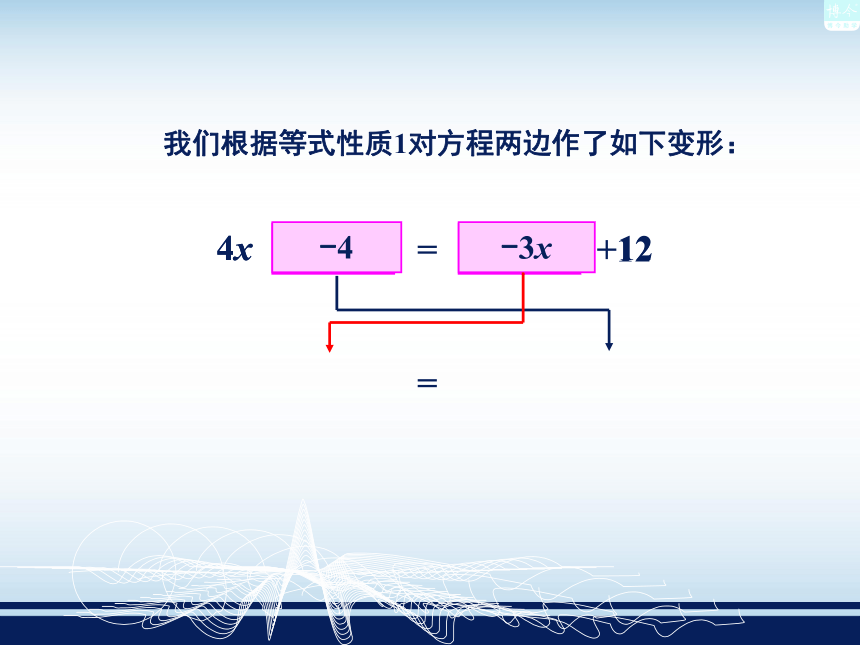
我们根据等式性质1对方程两边作了如下变形：
4x
+ 4
=
3 x
+12
4x
-3x
=
-4
12
把方程中的某一项改变符号后，从方程的一边移到另一边.我们把这种变形叫作移项.
结论
必须牢记：移项要变号.
4x
3x
=
+12
4x
+4
-3x
12
-4
=
例1 解下列方程：
（1）2x = x+3 ；
（2）3x -1 = 40 + 2x .
举
例
解
（1） 原方程为2x = x+3
将同类项放在一起
化简，得 x = 3
移项，得 2x -x = 3
所以 x=3 是原方程的解.
检验：把x=3代入原方程的左边和右边，
左边= 2×3=6，右边= 3+3=6，
左边=右边
计算结果
进行检验
解
（2） 原方程为3x -1 = 40 + 2x
将同类项放在一起
化简，得 x = 41
移项，得 3x -2x = 40+1
所以 x=41 是原方程的解.
检验：把x=41代入原方程的左边和右边，
左边= 3×41-1=122，右边= 40+2×41=122，
左边=右边
计算结果
进行检验
练习
1. 下面的移项对吗？如不对，请你改正.
（1）从x -4 = 8，得x = 8-4；
（2）从3x = 2x+5，得3x-2x = 5；
（3）从5x-2 = 4x+1，得5x-4x = 1+2.
不对，移项没有变号，应为x = 8+4
对
对
2. 通过移项解下列方程，并写出检验.
（1）x +4 = 5； （2）-5 + x = -4；
（3）13x+8=12x； （4）7x-3=6x-4 .
解
（1） 原方程为x +4 = 5
移项，得 x = 5-4
化简，得 x = 1
检验：把x=1代入原方程的左边和右边，
左边= 1+4=5，右边= 5，
左边=右边
所以 x=1 是原方程的解.
（2） 原方程为-5 + x = -4
移项，得 x = 5-4
化简，得 x = 1
检验：把x=1代入原方程的左边和右边，
左边= -5+1=-4，右边= -4，
左边=右边
所以 x=1 是原方程的解.
（3） 原方程为13x+8=12x
移项，得 13x-12x = -8
化简，得 x = -8
检验：把x=-8代入原方程的左边和右边，
左边=13×(-8)+8=-96，右边= 12 ×(-8)=-96，
左边=右边
所以 x=-8 是原方程的解.
（4） 原方程为7x-3=6x-4
移项，得 7x-6x = 3-4
化简，得 x = -1
检验：把x=-1代入原方程的左边和右边，
左边= 7×(-1)-3=-10，右边=6×(-1)-4=-10，
左边=右边
所以 x=-1 是原方程的解.
动脑筋
某实验中学举行田径运动会.七年级甲班和丙班参加的人数的和是乙班参加的人数的3倍，甲班有40人参加，乙班参加的人数比丙班参加的人数少10人.
你能算出乙班参加校运会的人数吗？
分析：设乙班参加校运动会的人数为x，那么，丙班参加的人数就是（x+10）人.根据题意你能说出甲、乙、丙三个班参加校运动会人数之间的等量关系吗？
甲班参加的人数+丙班参加的人数=乙班参加的人数的3倍.
按这个等量关系，得
3x=40+x+10
移项，得 3x -x = 50
化简，得 2x = 50
这样的方程如何来解呢？
根据等式性质2，方程 2x = 50可以这样来解.
把两边都除以2，得
化简，得 x = 25
检验：把 x = 25代入原方程的左边和右边，得
左边=3×25=75，右边=40+25+10=75，
左边=右边
所以x=25是原方程的解.
答：乙班有25人参加校运会.
例2 解下列方程：
（1）11x-2 = 8x-8 ；
（2）2x -3 = 7 - x .
举
例
解
（1） 原方程为11x-2 = 8x-8
将同类项放在一起
化简，得 3x = -6
移项，得 11x -8x = -8+2
所以 x=-2是原方程的解.
方程两边同除以3，得
左边=11×(-2)-2=-24，右边=8×(-2)-8=-24 ，
左边=右边
计算结果
进行检验
=
化简，得 x = -2
检验：把x=-2代入原方程的左边和右边，得
将同类项放在一起
左边=右边
计算结果
进行检验
解
（2） 原方程为2x -3 = 7 - x
移项，得 2x + x = 3+7
化简，得 x = 10
方程两边同除以 ，得
÷ = 10÷
化简，得 x =
检验：把x= 代入原方程的左边和右边，得
左边=2× -3= ，右边=7- × = ，
所以 x= 是原方程的解.
练习
1. 下列解法对吗？如不对，应当怎样改正.
（3）从7x-3 = 5x-1，得7x-5x =-1+3，得2x=2，得x=1.
对
（1）从 x = ，得x = 1；
（2）从5x+2=0，得5x = -2，得x= - ；
不对，x =
不对，x = -
2. 解下列方程：
（1） 2.4x+2.4 = 6.8-2x ；
（2） x + 4 = 12 -2(x-2) .
解
（1） 原方程为2.4x+2.4 = 6.8-2x
移项，得 2.4x+2x = -2.4+6.8
化简，得 x = 1
检验：把x=1代入原方程的左边和右边，
左边= 2.4×1+2.4=4.8，
右边= 6.8-2×1=4.8 ，
左边=右边
所以 x=1 是原方程的解.
（2） 原方程为 x + 4 = 12-2(x-2)
移项，得 x+2x = -4+12+4
化简，得 x = 5
检验：把x=5代入原方程的左边和右边，
左边= ×5 + 4= 6，
右边= 12-2(5-2)= 6，
左边=右边
所以 x=5 是原方程的解.
动脑筋
现有树苗若干棵，计划栽在一段公路的一侧，要求路的两端各栽1棵，并且每2棵树的间隔相等.如果每隔5m栽1棵，则树苗缺21棵；如果每隔5.5m栽1棵，则树苗正好用完.
你能算出原有树苗的棵数和这段路的长度吗？
分析：观察下面植树示意图4-3，想一想：
（1）相邻两树的间隔长与应植树的棵数有什么关系？
（2）相邻两树的间隔长、应植树棵数与路长有怎样的数
量关系？
图4-3
图4-3
方案 间隔长 应植树数 路长
方案一 5 x+21 5(x+21-1)
方案二 5.5 x 5.5(x-1)
设原有树苗x棵，根据题意，得
由于是同一段路上植树，路长相等，所以有
5(x+21-1)=5.5(x-1)，
即
5(x+20)=5.5(x-1)，
这个方程与本章前面的方程比较，方程中多了括号，妨碍了移项，那么这样的方程如何解呢？
用分配律，得
5x+100 = 5.5x-5.5
移项，得
5x-5.5 x= -5.5-100
化简，得
-0.5 x= -105.5
方程两边都除以-0.5，得 x=211
5(x+20)=5×(211+20)=1155.
答：原有树苗211棵，这段路的长度为1155m.
例3 解方程：
举
例
解
去括号将同类项放在一起
注：
检验的过程不用再书写出来，但还是要求同学们自己进行检验，以后解一元一次方程也这样.
去括号，得 x-5- x+2=x
移项，得 x - x -x= 5-2
化简，得 - x = 3
方程两边同除以 - ，得
x = -
化简
计算结果
练习
1. 下面方程解法对不对？如不对，请改正.
解方程 (2x+3)=2+x
解 去括号，得 x+3=2+x
移项，得 x +x = 2-3
化简，得 x = -1
方程两边同除以 ，得
x = -
应改为 x + =2+x
应改为 x – x = 2-
应改为 - x =
应改为 x = -4
2. 解下列方程，并用口算检验.
（1） (4y+8)+(3y-7)= 0 ；
（2） 2(2x -1)-2(4x+3)= 7；
（3） (x -4)= 3x.
解
（1） 原方程为(4y+8)+(3y-7)= 0
去括号，得 4y+8+3y-7= 0
移项，得 4y+3y = 7-8
化简，得 7y = -1
方程两边同除以 7， y = -
（2） 原方程为2(2x -1)-2(4x+3)= 7
去括号，得 4x-2-8x-6= 7
移项，得 4x-8x = 2+6+7
化简，得 -4x = 15
方程两边同除以 -4， x = -
（3） 原方程为 (x -4)= 3x
去括号，得 x -3 = 3x
移项，得 x -3x = 3
化简，得 - x = 3
方程两边同除以 - ，
x = -
动脑筋
一件工作，甲单独做需要15天完成，乙单独做需要12天完成.现在甲先单独做1天，接着乙又单独做4天，剩下的工作由甲、乙两个合做.问合做多少天可以完成全部工作任务？
你能说出问题中的等量关系吗？
分析：
设工作总量为1，甲每天完成工作总量的 ，乙每天完成工作总量的 .
=工作总量.
如果剩下的工作两人合做需要x天完成，那么甲做了(x+1)天，完成的工作量为 .乙做了(x+4)天，完成的工作量为 .
根据题意，得
如果先去括号，则会多次遇到分数的运算，较繁.那么这类方程是否有较简便的解法呢？
根据等式性质2，把方程两边都乘各分母的最小公倍数60，就可以把分母去掉.
于是，得
化简，得 4(x+1)+5(x+4)=60 .
去括号，得 4x+4+5x+20=60 .
移项，得 9x=36 .
方程两边都除以9，得 x=4.
答：两人再合做4天，可完成全部任务.
例4 解方程：
举
例
解
先去分母，再计算
去括号，得 4x -40 = 3x-18
移项，得 4x -3x = -18 + 40
化简，得 x = 22
去分母，得 ×12 = ×12
4(x-10)= 3(x-6)
去括号，再计算
移项，将同类项放在一起
解一元一次方程的一般步骤是：
一元一次方程
先去分母，后去括号，
再移项和化简得
a x = b（a ≠ 0）
x =
两边同时除以a
练习
1. 下面各题中的去分母对吗？如不对，请改正.
（1） - = 2，去分母得5x-2x+3 = 2；
（2） - = 1，去分母得2x-(2x+1)= 6；
（3） + = 4，去分母得4(3x+1)+25x= 80.
不对，应为 25x-3(2x-3)=30
不对，应为 4x-(2x+1)=6
对
2. 解下列方程：
（1） = ；
（2） - = 1.
解:
去分母，得 × 6 = × 6
(5-3x)×3 = (3+5x)×2
去括号，得 15-9x = 6+10x
移项，得 -9x -10x = 6-15
化简，得 -19x = -9
方程两边同除以 -19， x =
（1） =
解:
去分母，得 × 24 - × 24 =1
(2x-1)×4 - (5x+1)×3=1×24
去括号，得 8x -4 -15x – 3 =24
移项，得 8x -15x = 4+3+24
化简，得 -7x = 31
方程两边同除以 -7， x = -
（2） - = 1.
解
中考 试题
例1
分析
C
因为 的倒数是 ，根据“互为相反数之和等于0”可得 ，解方程即可求出a的值.
由已知条件可得 ，去分母，得a+2a-9=0，合并同类项，得3a=9，系数化为1，得a=3.
故，应选择C.
的倒数与 互为相反数，那么a的值为（ ）.
A. B. C.3 D.-3
解
中考 试题
例2
解方程 .
分析
本题如果按解一元一次方程的一般步骤去解，则比较复杂，观察方程的特点，可以看出本题若采用由外及里的方法去括号，可使运算较简单.
去中括号，得 ，即
移项，得 .
∴ x =
解
中考 试题
例3
方程 的解是（ ）.
A. B. C. D.
方程两边同乘以6，得
去中括号，得
移项，合并同类项，得
去小括号，得
合并同类项，得
去分母，得
移项，得
合并同类项，得
两边同除以一次项系数，得
故，应选择A.
A
结 束