2020-2021学年北师大版八年级数学下册第1章三角形的证明单元练习(word解析版)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册第1章三角形的证明单元练习(word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 191.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-30 00:00:00 | ||
图片预览



文档简介
北师大版八年级数学下册第一章三角形的证明 同步练习
一.选择题
1.如图,OM.ON.OP分别是∠AOB,∠BOC,∠AOC的角平分线,则下列选项成立的( )
A.∠AOP>∠MON B.∠AOP=∠MON
C.∠AOP<∠MON D.以上情况都有可能
2.如果一个等腰三角形的两条边长分别为3和7,那么这个等腰三角形的周长为( )
A.13 B.17 C.13或17 D.以上都不是
3.在中,,的垂直平分线交于点,交于点,且,则为( ?).
?A. ???B. ?C. D. 无法确定
4.在平面直角坐标系中,等腰△ABC的顶点A.B的坐标分别为(0,0).(2,2),若顶点C落在坐标轴上,则符合条件的点C有( )个.
A.5 B.6 C.7 D.8
5.如图所示,∠C=∠D=90°,添加下列条件①AC=AD;②∠ABC=∠ABD; ③∠BAC=∠BAD; ④BC=BD,能判定Rt△ABC与Rt△ABD全等的条件的个数是( )
A.1 B.2 C.3 D.4
6.如图,在中,,是边上中线.若,,则的周长是( ?)?
A. ??B. ??C. ?D.
7.下列条件中,能判定两个直角三角形全等的是( )
????A. 一锐角对应相等 B. 两锐角对应相等
????C. 一条边对应相等 ???D. 两条直角边对应相等
8.如图,A,B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC为等腰三角形,满足条件的点C有( )
A.6个 B.7个 C.8个 D.9个
9.如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=3,则两平行线AD与BC间的距离为( )
A.3 B.4 C.5 D.6
10.如图,在中,,平分,于.如果,,那么等于( )
????A. ????B. ??C. ?D.
11.下列命题正确的是( )
A.绝对值等于本身的数是正数
B.绝对值等于相反数的数是负数
C.互为相反数的两个数的绝对值相等
D.绝对值相等的两个数互为相反数
12.用反证法证明命题“四边形中至少有一个角是钝角或直角”,应首先假设这个四边形中( )
A.没有一个角是锐角
B.每一个角都是钝角或直角
C.至少有一个角是钝角或直角
D.所有角都是锐角
E.所有角都是直角
二.填空题
13.结合图,用符号语言表达定理“斜边和一条直角边分别相等的两个直角三角形全等”的推理形式:
在Rt△ABC和Rt△DEF中,∠C=∠F=90°,
AC=DF
∴Rt△ABC≌Rt△DEF.
14.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于D点.若BD平分∠ABC,则∠A= °.
15.如图所示,在△ABC中,DE,MN是边AB.AC的垂直平分线,其垂足分别为D.M,分别交BC于E.N,若AB=8,AC=9,设△AEN周长为m,则m的取值范围为 .
16.已知的平分线上一点,到的距离为,则到的距离为????????????.
17.举出一个m的值,说明命题“代数式2m2﹣1的值一定大于代数式m2﹣1的值”是错误的,那么这个m的值可以是 .
18.如图是4×4的正方形网格,每个小正方形的顶点称为格点,且边长为1,点A,B均在格点上,在网格中建立平面直角坐标系.如果点C也在此4×4的正方形网格的格点上,且△ABC是等腰三角形,请写出一个满足条件的点C的坐标 ;满足条件的点C一共有 个.
三.解答题
19.如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.
20.求证:一条直角边相等且另一条直角边上中线相等的两个直角三角形全等.
已知:如图,△ABC和△DEF中,∠B=∠E=90°,BC=EF,BM为△ABC的中线,FN为△DEF的中线,且CM=FN,
求证:△ABC≌△DEF.
21.已知一个等腰三角形的周长为,有一边长为,则这个三角形的边长是多少?
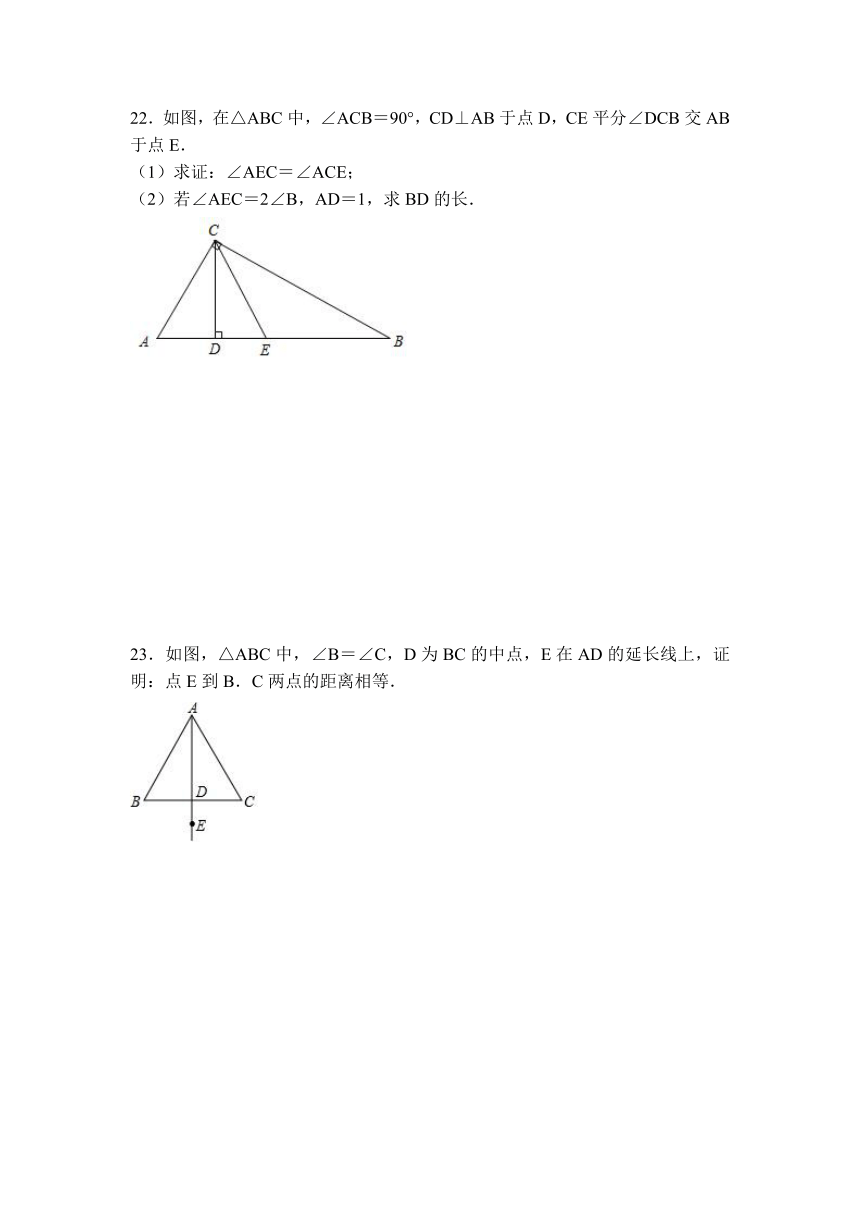
22.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)求证:∠AEC=∠ACE;
(2)若∠AEC=2∠B,AD=1,求BD的长.
23.如图,△ABC中,∠B=∠C,D为BC的中点,E在AD的延长线上,证明:点E到B.C两点的距离相等.
24.在数学实践课上,老师在黑板上画出如下的图形(其中点B.F.C.E在同一条直线上),并写出四个条件:①AB=DE,②∠1=∠2.③BF=EC,④∠B=∠E,交流中老师让同学们从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.
(1)写出所有的真命题.(用序号表示题设.结论)
(2)请选择一个给予证明.
25.如图,在△ABC中,AB=AC=8,AB的垂直平分线交AB于点D,交AC于点E.
(1)若BE﹣EC=2,求CE的长;
(2)若∠A=36o,求证:△BEC是等腰三角形.
北师大版八年级数学下册第一章三角形的证明 同步测试答案
一.选择题
1.如图,OM.ON.OP分别是∠AOB,∠BOC,∠AOC的角平分线,则下列选项成立的( )
A.∠AOP>∠MON B.∠AOP=∠MON
C.∠AOP<∠MON D.以上情况都有可能
解:∵OM.ON分别是∠AOB,∠BOC的角平分线,
∴∠BOM=∠AOB,∠BON=∠BOC,
∴∠MON=∠BOM+∠BON=(∠AOB+∠BOC)=∠AOC,
∵OP是∠AOC的角平分线,
∴∠AOP=∠AOC,
∴∠AOP=∠MON,
故选:B.
2.如果一个等腰三角形的两条边长分别为3和7,那么这个等腰三角形的周长为( )
A.13 B.17 C.13或17 D.以上都不是
解:当3是腰时,则3+3<7,不能组成三角形,应舍去;
当7是腰时,则三角形的周长是3+7×2=17.
故选:B.
3.在中,,的垂直平分线交于点,交于点,且,则为( ?).
????A. ???B. ?C. D. 无法确定
解:如图所示.
,且平分,
,
是等腰三角形,
,
,
,
,
而,且,
,
解得.
故正确答案是:.
4.在平面直角坐标系中,等腰△ABC的顶点A.B的坐标分别为(0,0).(2,2),若顶点C落在坐标轴上,则符合条件的点C有( )个.
A.5 B.6 C.7 D.8
解:①若AC=AB,则以点A为圆心,AB为半径画圆,与坐标轴有4个交点;
②若BC=BA,则以点B为圆心,BA为半径画圆,与坐标轴有2个交点(A点除外);
③若CA=CB,则点C在AB的垂直平分线上,
∵A(0,0),B(2,2),
∴AB的垂直平分线与坐标轴有2个交点.
综上所述:符合条件的点C的个数有8个.
故选:D.
5.如图所示,∠C=∠D=90°,添加下列条件①AC=AD;②∠ABC=∠ABD; ③∠BAC=∠BAD; ④BC=BD,能判定Rt△ABC与Rt△ABD全等的条件的个数是( )
A.1 B.2 C.3 D.4
解:①当AC=AD时,由∠C=∠D=90°,AC=AD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);
②当∠ABC=∠ABD时,由∠C=∠D=90°,∠ABC=∠ABD且AB=AB,可得Rt△ABC≌Rt△ABD(AAS);
③当∠BAC=∠BAD时,由∠C=∠D=90°,∠BAC=∠BAD且AB=AB,可得Rt△ABC≌Rt△ABD(AAS);
④当BC=BD时,由∠C=∠D=90°,BC=BD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);
故选:D.
6.如图,在中,,是边上中线.若,,则的周长是( ?)?
????A. ??B. ??C. ?D.
解:,是边上中线,
,,
,
,
的周长.
7.下列条件中,能判定两个直角三角形全等的是( )
????A. 一锐角对应相等 B. 两锐角对应相等
????C. 一条边对应相等 ???D. 两条直角边对应相等
解:两直角三角形隐含一个条件是两直角相等,要判定两直角三角形全等,起码还要两个条件,故可排除“一锐角对应相等”.“一条边对应相等”;
而“两锐角对应相等”构成了,不能判定全等;
“两条直角边对应相等”构成了,可以判定两个直角三角形全等.
8.如图,A,B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC为等腰三角形,满足条件的点C有( )
A.6个 B.7个 C.8个 D.9个
解:①点C以点A为标准,AB为底边,符合点C的有5个;
②点C以点B为标准,AB为等腰三角形的一条边,符合点C的有4个.
所以符合条件的点C共有9个.
故选:D.
9.如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=3,则两平行线AD与BC间的距离为( )
A.3 B.4 C.5 D.6
解:如图,过点P作PF⊥AD于F,作PG⊥BC于G,
∵AP是∠BAD的平分线,PE⊥AB,
∴PF=PE,
同理可得PG=PE,
∵AD∥BC,
∴点F.P.G三点共线,
∴FG的长即为AD.BC间的距离,
∴平行线AD与BC间的距离为3+3=6,
故选:D.
10.如图,在中,,平分,于.如果,,那么等于( )
????A. ????B. ??C. ?D.
解:,,
,
,
,
,平分,
,
.
11.下列命题正确的是( )
A.绝对值等于本身的数是正数
B.绝对值等于相反数的数是负数
C.互为相反数的两个数的绝对值相等
D.绝对值相等的两个数互为相反数
解:A.绝对值等于本身的数是非负数,原命题是假命题;
B.绝对值等于相反数的数是非正数,原命题是假命题;
C.互为相反数的两个数的绝对值相等,是真命题;
D.绝对值相等的两个数相等或互为相反数,原命题是假命题;
故选:C.
12.用反证法证明命题“四边形中至少有一个角是钝角或直角”,应首先假设这个四边形中( )
A.没有一个角是锐角
B.每一个角都是钝角或直角
C.至少有一个角是钝角或直角
D.所有角都是锐角
E.所有角都是直角
解:用反证法证明“四边形中至少有一个角是钝角或直角”时第一步应假设:四边形中所有角都是锐角.
故选:D.
二.填空题
13.结合图,用符号语言表达定理“斜边和一条直角边分别相等的两个直角三角形全等”的推理形式:
在Rt△ABC和Rt△DEF中,∠C=∠F=90°,
AC=DF
AB=DE
∴Rt△ABC≌Rt△DEF.
解:∵∠C=∠F=90°,
∴在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
故答案为:AB=DE.
14.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于D点.若BD平分∠ABC,则∠A= 36 °.
解:∵AB=AC,
∴∠C=∠ABC,
∵AB的垂直平分线MN交AC于D点.
∴∠A=∠ABD,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠C=2∠A=∠ABC,
设∠A为x,
可得:x+x+x+2x=180°,
解得:x=36°,
故答案为:36
15.如图所示,在△ABC中,DE,MN是边AB.AC的垂直平分线,其垂足分别为D.M,分别交BC于E.N,若AB=8,AC=9,设△AEN周长为m,则m的取值范围为 <m<17 .
解:∵DE,MN是边AB.AC的垂直平分线,
∴EA=EB,NC=NA,
∴△AEN周长为m=EA+EN+NA=EB+EN+NC=BC,
在△ABC中,9﹣8<BC<9+8,
∴m<17,
当∠BAC=90°时,BC==,
∴<m<17
故答案为:<m<17.
16.已知的平分线上一点,到的距离为,则到的距离为????????????.
解:是的平分线上一点,
根据定理:角平分线上的点到角的两边距离相等.
点到的距离等于到的距离,
到的距离为,
到的距离为.
故答案为:.
17.举出一个m的值,说明命题“代数式2m2﹣1的值一定大于代数式m2﹣1的值”是错误的,那么这个m的值可以是 m=0 .
解:当m=0时,2m2﹣1=﹣1,m2﹣1=﹣1,
此时2m2﹣1=m2﹣1,
故答案为:m=0.
18.如图是4×4的正方形网格,每个小正方形的顶点称为格点,且边长为1,点A,B均在格点上,在网格中建立平面直角坐标系.如果点C也在此4×4的正方形网格的格点上,且△ABC是等腰三角形,请写出一个满足条件的点C的坐标 (﹣2,0),(﹣2,1),(﹣2,2),(2,2),(2,0),(1,0),(1,﹣1),(1,﹣2), ;满足条件的点C一共有 8 个.
解:满足条件的点C的坐标为(﹣2,0),(﹣2,1),(﹣2,2),(2,2),(2,0),(1,0),(1,﹣1),(1,﹣2),满足条件的点C一共有8个,
故答案为:(﹣2,0),(﹣2,1),(﹣2,2),(2,2),(2,0),(1,0),(1,﹣1),(1,﹣2),8.
三.解答题
19.如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.
证明:(1)在△ABC和△DCB中,∠A=∠D=90°
AC=BD,BC为公共边,
∴Rt△ABC≌Rt△DCB(HL);
(2)△OBC是等腰三角形
∵Rt△ABC≌Rt△DCB
∴∠ACB=∠DCB
∴OB=OC
∴△OBC是等腰三角形
20.求证:一条直角边相等且另一条直角边上中线相等的两个直角三角形全等.
已知:如图,△ABC和△DEF中,∠B=∠E=90°,BC=EF,BM为△ABC的中线,FN为△DEF的中线,且CM=FN,
求证:△ABC≌△DEF.
证明:在Rt△BCM和Rt△EFN中
,
∴Rt△BCM≌Rt△EFN(HL),
∴BM=EN,
∵BM为△ABC的中线,FN为△DEF的中线,
∴AB=DE,
在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS).
即一条直角边相等且另一条直角边上中线相等的两个直角三角形全等.
21.已知一个等腰三角形的周长为,有一边长为,则这个三角形的边长是多少?
解:当是腰长时,则底边为,这时,三边长为..
当是底边时,则腰长为:,这时,三边长为..
故三角形三边是..或...
22.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)求证:∠AEC=∠ACE;
(2)若∠AEC=2∠B,AD=1,求BD的长.
解:(1)∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠A=∠B+∠A=90°,
∴∠ACD=∠B,
∵CE平分∠BCD,
∴∠BCE=∠DCE,
∴∠B+∠BCE=∠ACD+∠DCE,
即∠AEC=∠ACE;
(2)∵∠AEC=∠B+∠BCE,∠AEC=2∠B,
∴∠B=∠BCE,
又∵∠ACD=∠B,∠BCE=∠DCE,
∴∠ACD=∠BCE=∠DCE,
又∵∠ACB=90°,
∴∠ACD=30°,∠B=30°,
∴Rt△ACD中,AC=2AD=2,
∴Rt△ABC中,AB=2AC=4,
∴BD=AB﹣AD=4﹣1=3.
23.如图,△ABC中,∠B=∠C,D为BC的中点,E在AD的延长线上,证明:点E到B.C两点的距离相等.
解:∵∠B=∠C,
∴AB=AC,
∵D为BC的中点,
∴AD⊥BC,
∴AD垂直平分BC,
∵E在AD上,
∴点E到B.C两点的距离相等.
24.在数学实践课上,老师在黑板上画出如下的图形(其中点B.F.C.E在同一条直线上),并写出四个条件:①AB=DE,②∠1=∠2.③BF=EC,④∠B=∠E,交流中老师让同学们从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.
(1)写出所有的真命题.(用序号表示题设.结论)
(2)请选择一个给予证明.
解:(1)情况一:题设:①②④;结论:③;
情况二:题设①③④;结论:②;
情况三:题设②③④;结论:①.
(2)选择的题设:①③④;结论:②;
理由:∵BF=EC,
∴BF+CF=EC+CF,即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠1=∠2;
25.如图,在△ABC中,AB=AC=8,AB的垂直平分线交AB于点D,交AC于点E.
(1)若BE﹣EC=2,求CE的长;
(2)若∠A=36o,求证:△BEC是等腰三角形.
(1)解:∵AB的垂直平分线交AB于点D,
∴EA=EB,
∴AE=AC﹣EC=8﹣x,
∵BE﹣EC=2,
∴BE=EC+2,
∴8﹣EC=EC+2,
∴CE=3;
(2)证明:∵EA=EB,
∴∠EBA=∠A=36°,
∴∠BEC=∠A+∠EBA=72°,
∵AB=AC,
∴∠ABC=∠C=(180°﹣∠A)=(180°﹣36°)=72°,
∴∠C=∠BEC,
∴△BEC是等腰三角形.
一.选择题
1.如图,OM.ON.OP分别是∠AOB,∠BOC,∠AOC的角平分线,则下列选项成立的( )
A.∠AOP>∠MON B.∠AOP=∠MON
C.∠AOP<∠MON D.以上情况都有可能
2.如果一个等腰三角形的两条边长分别为3和7,那么这个等腰三角形的周长为( )
A.13 B.17 C.13或17 D.以上都不是
3.在中,,的垂直平分线交于点,交于点,且,则为( ?).
?A. ???B. ?C. D. 无法确定
4.在平面直角坐标系中,等腰△ABC的顶点A.B的坐标分别为(0,0).(2,2),若顶点C落在坐标轴上,则符合条件的点C有( )个.
A.5 B.6 C.7 D.8
5.如图所示,∠C=∠D=90°,添加下列条件①AC=AD;②∠ABC=∠ABD; ③∠BAC=∠BAD; ④BC=BD,能判定Rt△ABC与Rt△ABD全等的条件的个数是( )
A.1 B.2 C.3 D.4
6.如图,在中,,是边上中线.若,,则的周长是( ?)?
A. ??B. ??C. ?D.
7.下列条件中,能判定两个直角三角形全等的是( )
????A. 一锐角对应相等 B. 两锐角对应相等
????C. 一条边对应相等 ???D. 两条直角边对应相等
8.如图,A,B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC为等腰三角形,满足条件的点C有( )
A.6个 B.7个 C.8个 D.9个
9.如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=3,则两平行线AD与BC间的距离为( )
A.3 B.4 C.5 D.6
10.如图,在中,,平分,于.如果,,那么等于( )
????A. ????B. ??C. ?D.
11.下列命题正确的是( )
A.绝对值等于本身的数是正数
B.绝对值等于相反数的数是负数
C.互为相反数的两个数的绝对值相等
D.绝对值相等的两个数互为相反数
12.用反证法证明命题“四边形中至少有一个角是钝角或直角”,应首先假设这个四边形中( )
A.没有一个角是锐角
B.每一个角都是钝角或直角
C.至少有一个角是钝角或直角
D.所有角都是锐角
E.所有角都是直角
二.填空题
13.结合图,用符号语言表达定理“斜边和一条直角边分别相等的两个直角三角形全等”的推理形式:
在Rt△ABC和Rt△DEF中,∠C=∠F=90°,
AC=DF
∴Rt△ABC≌Rt△DEF.
14.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于D点.若BD平分∠ABC,则∠A= °.
15.如图所示,在△ABC中,DE,MN是边AB.AC的垂直平分线,其垂足分别为D.M,分别交BC于E.N,若AB=8,AC=9,设△AEN周长为m,则m的取值范围为 .
16.已知的平分线上一点,到的距离为,则到的距离为????????????.
17.举出一个m的值,说明命题“代数式2m2﹣1的值一定大于代数式m2﹣1的值”是错误的,那么这个m的值可以是 .
18.如图是4×4的正方形网格,每个小正方形的顶点称为格点,且边长为1,点A,B均在格点上,在网格中建立平面直角坐标系.如果点C也在此4×4的正方形网格的格点上,且△ABC是等腰三角形,请写出一个满足条件的点C的坐标 ;满足条件的点C一共有 个.
三.解答题
19.如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.
20.求证:一条直角边相等且另一条直角边上中线相等的两个直角三角形全等.
已知:如图,△ABC和△DEF中,∠B=∠E=90°,BC=EF,BM为△ABC的中线,FN为△DEF的中线,且CM=FN,
求证:△ABC≌△DEF.
21.已知一个等腰三角形的周长为,有一边长为,则这个三角形的边长是多少?
22.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)求证:∠AEC=∠ACE;
(2)若∠AEC=2∠B,AD=1,求BD的长.
23.如图,△ABC中,∠B=∠C,D为BC的中点,E在AD的延长线上,证明:点E到B.C两点的距离相等.
24.在数学实践课上,老师在黑板上画出如下的图形(其中点B.F.C.E在同一条直线上),并写出四个条件:①AB=DE,②∠1=∠2.③BF=EC,④∠B=∠E,交流中老师让同学们从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.
(1)写出所有的真命题.(用序号表示题设.结论)
(2)请选择一个给予证明.
25.如图,在△ABC中,AB=AC=8,AB的垂直平分线交AB于点D,交AC于点E.
(1)若BE﹣EC=2,求CE的长;
(2)若∠A=36o,求证:△BEC是等腰三角形.
北师大版八年级数学下册第一章三角形的证明 同步测试答案
一.选择题
1.如图,OM.ON.OP分别是∠AOB,∠BOC,∠AOC的角平分线,则下列选项成立的( )
A.∠AOP>∠MON B.∠AOP=∠MON
C.∠AOP<∠MON D.以上情况都有可能
解:∵OM.ON分别是∠AOB,∠BOC的角平分线,
∴∠BOM=∠AOB,∠BON=∠BOC,
∴∠MON=∠BOM+∠BON=(∠AOB+∠BOC)=∠AOC,
∵OP是∠AOC的角平分线,
∴∠AOP=∠AOC,
∴∠AOP=∠MON,
故选:B.
2.如果一个等腰三角形的两条边长分别为3和7,那么这个等腰三角形的周长为( )
A.13 B.17 C.13或17 D.以上都不是
解:当3是腰时,则3+3<7,不能组成三角形,应舍去;
当7是腰时,则三角形的周长是3+7×2=17.
故选:B.
3.在中,,的垂直平分线交于点,交于点,且,则为( ?).
????A. ???B. ?C. D. 无法确定
解:如图所示.
,且平分,
,
是等腰三角形,
,
,
,
,
而,且,
,
解得.
故正确答案是:.
4.在平面直角坐标系中,等腰△ABC的顶点A.B的坐标分别为(0,0).(2,2),若顶点C落在坐标轴上,则符合条件的点C有( )个.
A.5 B.6 C.7 D.8
解:①若AC=AB,则以点A为圆心,AB为半径画圆,与坐标轴有4个交点;
②若BC=BA,则以点B为圆心,BA为半径画圆,与坐标轴有2个交点(A点除外);
③若CA=CB,则点C在AB的垂直平分线上,
∵A(0,0),B(2,2),
∴AB的垂直平分线与坐标轴有2个交点.
综上所述:符合条件的点C的个数有8个.
故选:D.
5.如图所示,∠C=∠D=90°,添加下列条件①AC=AD;②∠ABC=∠ABD; ③∠BAC=∠BAD; ④BC=BD,能判定Rt△ABC与Rt△ABD全等的条件的个数是( )
A.1 B.2 C.3 D.4
解:①当AC=AD时,由∠C=∠D=90°,AC=AD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);
②当∠ABC=∠ABD时,由∠C=∠D=90°,∠ABC=∠ABD且AB=AB,可得Rt△ABC≌Rt△ABD(AAS);
③当∠BAC=∠BAD时,由∠C=∠D=90°,∠BAC=∠BAD且AB=AB,可得Rt△ABC≌Rt△ABD(AAS);
④当BC=BD时,由∠C=∠D=90°,BC=BD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);
故选:D.
6.如图,在中,,是边上中线.若,,则的周长是( ?)?
????A. ??B. ??C. ?D.
解:,是边上中线,
,,
,
,
的周长.
7.下列条件中,能判定两个直角三角形全等的是( )
????A. 一锐角对应相等 B. 两锐角对应相等
????C. 一条边对应相等 ???D. 两条直角边对应相等
解:两直角三角形隐含一个条件是两直角相等,要判定两直角三角形全等,起码还要两个条件,故可排除“一锐角对应相等”.“一条边对应相等”;
而“两锐角对应相等”构成了,不能判定全等;
“两条直角边对应相等”构成了,可以判定两个直角三角形全等.
8.如图,A,B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC为等腰三角形,满足条件的点C有( )
A.6个 B.7个 C.8个 D.9个
解:①点C以点A为标准,AB为底边,符合点C的有5个;
②点C以点B为标准,AB为等腰三角形的一条边,符合点C的有4个.
所以符合条件的点C共有9个.
故选:D.
9.如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=3,则两平行线AD与BC间的距离为( )
A.3 B.4 C.5 D.6
解:如图,过点P作PF⊥AD于F,作PG⊥BC于G,
∵AP是∠BAD的平分线,PE⊥AB,
∴PF=PE,
同理可得PG=PE,
∵AD∥BC,
∴点F.P.G三点共线,
∴FG的长即为AD.BC间的距离,
∴平行线AD与BC间的距离为3+3=6,
故选:D.
10.如图,在中,,平分,于.如果,,那么等于( )
????A. ????B. ??C. ?D.
解:,,
,
,
,
,平分,
,
.
11.下列命题正确的是( )
A.绝对值等于本身的数是正数
B.绝对值等于相反数的数是负数
C.互为相反数的两个数的绝对值相等
D.绝对值相等的两个数互为相反数
解:A.绝对值等于本身的数是非负数,原命题是假命题;
B.绝对值等于相反数的数是非正数,原命题是假命题;
C.互为相反数的两个数的绝对值相等,是真命题;
D.绝对值相等的两个数相等或互为相反数,原命题是假命题;
故选:C.
12.用反证法证明命题“四边形中至少有一个角是钝角或直角”,应首先假设这个四边形中( )
A.没有一个角是锐角
B.每一个角都是钝角或直角
C.至少有一个角是钝角或直角
D.所有角都是锐角
E.所有角都是直角
解:用反证法证明“四边形中至少有一个角是钝角或直角”时第一步应假设:四边形中所有角都是锐角.
故选:D.
二.填空题
13.结合图,用符号语言表达定理“斜边和一条直角边分别相等的两个直角三角形全等”的推理形式:
在Rt△ABC和Rt△DEF中,∠C=∠F=90°,
AC=DF
AB=DE
∴Rt△ABC≌Rt△DEF.
解:∵∠C=∠F=90°,
∴在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
故答案为:AB=DE.
14.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于D点.若BD平分∠ABC,则∠A= 36 °.
解:∵AB=AC,
∴∠C=∠ABC,
∵AB的垂直平分线MN交AC于D点.
∴∠A=∠ABD,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠C=2∠A=∠ABC,
设∠A为x,
可得:x+x+x+2x=180°,
解得:x=36°,
故答案为:36
15.如图所示,在△ABC中,DE,MN是边AB.AC的垂直平分线,其垂足分别为D.M,分别交BC于E.N,若AB=8,AC=9,设△AEN周长为m,则m的取值范围为 <m<17 .
解:∵DE,MN是边AB.AC的垂直平分线,
∴EA=EB,NC=NA,
∴△AEN周长为m=EA+EN+NA=EB+EN+NC=BC,
在△ABC中,9﹣8<BC<9+8,
∴m<17,
当∠BAC=90°时,BC==,
∴<m<17
故答案为:<m<17.
16.已知的平分线上一点,到的距离为,则到的距离为????????????.
解:是的平分线上一点,
根据定理:角平分线上的点到角的两边距离相等.
点到的距离等于到的距离,
到的距离为,
到的距离为.
故答案为:.
17.举出一个m的值,说明命题“代数式2m2﹣1的值一定大于代数式m2﹣1的值”是错误的,那么这个m的值可以是 m=0 .
解:当m=0时,2m2﹣1=﹣1,m2﹣1=﹣1,
此时2m2﹣1=m2﹣1,
故答案为:m=0.
18.如图是4×4的正方形网格,每个小正方形的顶点称为格点,且边长为1,点A,B均在格点上,在网格中建立平面直角坐标系.如果点C也在此4×4的正方形网格的格点上,且△ABC是等腰三角形,请写出一个满足条件的点C的坐标 (﹣2,0),(﹣2,1),(﹣2,2),(2,2),(2,0),(1,0),(1,﹣1),(1,﹣2), ;满足条件的点C一共有 8 个.
解:满足条件的点C的坐标为(﹣2,0),(﹣2,1),(﹣2,2),(2,2),(2,0),(1,0),(1,﹣1),(1,﹣2),满足条件的点C一共有8个,
故答案为:(﹣2,0),(﹣2,1),(﹣2,2),(2,2),(2,0),(1,0),(1,﹣1),(1,﹣2),8.
三.解答题
19.如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.
证明:(1)在△ABC和△DCB中,∠A=∠D=90°
AC=BD,BC为公共边,
∴Rt△ABC≌Rt△DCB(HL);
(2)△OBC是等腰三角形
∵Rt△ABC≌Rt△DCB
∴∠ACB=∠DCB
∴OB=OC
∴△OBC是等腰三角形
20.求证:一条直角边相等且另一条直角边上中线相等的两个直角三角形全等.
已知:如图,△ABC和△DEF中,∠B=∠E=90°,BC=EF,BM为△ABC的中线,FN为△DEF的中线,且CM=FN,
求证:△ABC≌△DEF.
证明:在Rt△BCM和Rt△EFN中
,
∴Rt△BCM≌Rt△EFN(HL),
∴BM=EN,
∵BM为△ABC的中线,FN为△DEF的中线,
∴AB=DE,
在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS).
即一条直角边相等且另一条直角边上中线相等的两个直角三角形全等.
21.已知一个等腰三角形的周长为,有一边长为,则这个三角形的边长是多少?
解:当是腰长时,则底边为,这时,三边长为..
当是底边时,则腰长为:,这时,三边长为..
故三角形三边是..或...
22.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)求证:∠AEC=∠ACE;
(2)若∠AEC=2∠B,AD=1,求BD的长.
解:(1)∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠A=∠B+∠A=90°,
∴∠ACD=∠B,
∵CE平分∠BCD,
∴∠BCE=∠DCE,
∴∠B+∠BCE=∠ACD+∠DCE,
即∠AEC=∠ACE;
(2)∵∠AEC=∠B+∠BCE,∠AEC=2∠B,
∴∠B=∠BCE,
又∵∠ACD=∠B,∠BCE=∠DCE,
∴∠ACD=∠BCE=∠DCE,
又∵∠ACB=90°,
∴∠ACD=30°,∠B=30°,
∴Rt△ACD中,AC=2AD=2,
∴Rt△ABC中,AB=2AC=4,
∴BD=AB﹣AD=4﹣1=3.
23.如图,△ABC中,∠B=∠C,D为BC的中点,E在AD的延长线上,证明:点E到B.C两点的距离相等.
解:∵∠B=∠C,
∴AB=AC,
∵D为BC的中点,
∴AD⊥BC,
∴AD垂直平分BC,
∵E在AD上,
∴点E到B.C两点的距离相等.
24.在数学实践课上,老师在黑板上画出如下的图形(其中点B.F.C.E在同一条直线上),并写出四个条件:①AB=DE,②∠1=∠2.③BF=EC,④∠B=∠E,交流中老师让同学们从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.
(1)写出所有的真命题.(用序号表示题设.结论)
(2)请选择一个给予证明.
解:(1)情况一:题设:①②④;结论:③;
情况二:题设①③④;结论:②;
情况三:题设②③④;结论:①.
(2)选择的题设:①③④;结论:②;
理由:∵BF=EC,
∴BF+CF=EC+CF,即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠1=∠2;
25.如图,在△ABC中,AB=AC=8,AB的垂直平分线交AB于点D,交AC于点E.
(1)若BE﹣EC=2,求CE的长;
(2)若∠A=36o,求证:△BEC是等腰三角形.
(1)解:∵AB的垂直平分线交AB于点D,
∴EA=EB,
∴AE=AC﹣EC=8﹣x,
∵BE﹣EC=2,
∴BE=EC+2,
∴8﹣EC=EC+2,
∴CE=3;
(2)证明:∵EA=EB,
∴∠EBA=∠A=36°,
∴∠BEC=∠A+∠EBA=72°,
∵AB=AC,
∴∠ABC=∠C=(180°﹣∠A)=(180°﹣36°)=72°,
∴∠C=∠BEC,
∴△BEC是等腰三角形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
