2020-2021学年北师大版八年级数学下册第3章图形的平移与旋转 单元练习(word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册第3章图形的平移与旋转 单元练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-30 14:10:55 | ||
图片预览

文档简介
北师大版八年级数学下册第三章图形的平移与旋转 同步练习
一.选择题
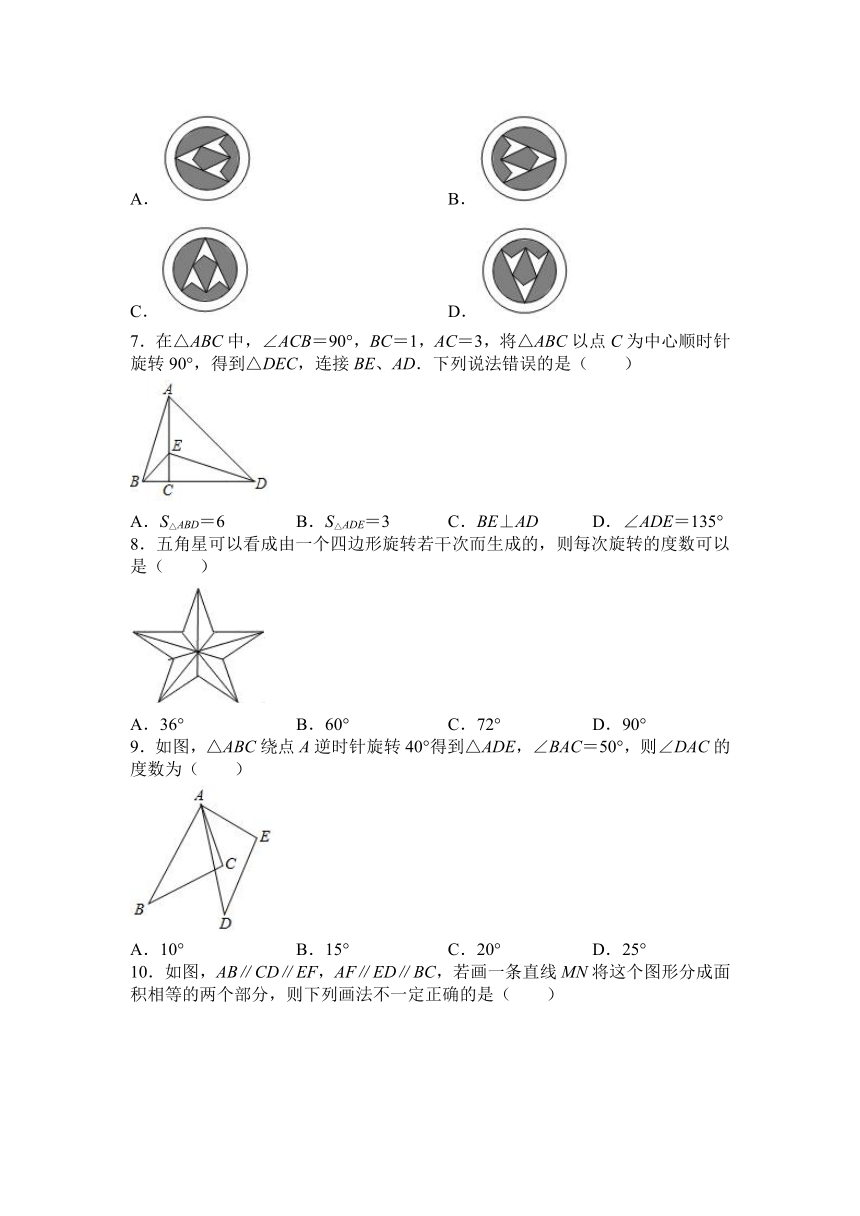
1.一木匠用了最少测量次数就测出了如图(图中所有的角为直角)工件的周长.则他测量的次数为( )
A.6次 B.5次 C.4次 D.3次
2.已知点P关于x轴对称的点的坐标为(2,﹣1),那么点P关于原点对称的点的坐标是( )
A.(1,﹣2) B.(2,1) C.(﹣2,﹣1) D.(﹣2,1)
3.在平面直角坐标系中,将点A(x,﹣y)向上平移2个单位长度,再向左平移3个单位长度,得到点A′,则点A′的坐标是( )
A.(x+3,2﹣y) B.(x+3,﹣y﹣2) C.(x﹣3,2﹣y) D.(x﹣3,﹣y﹣2)
4.如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
A.20cm B.22cm C.24cm D.26cm
5.如图,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在A1(﹣2,2)处,则点B的对应点B1的坐标为( )
A.(﹣1,﹣1) B.(﹣1,0) C.(1,0) D.(3,0)
6.下列图案中,能用原图平移得到的图案是( )
A. B.
C. D.
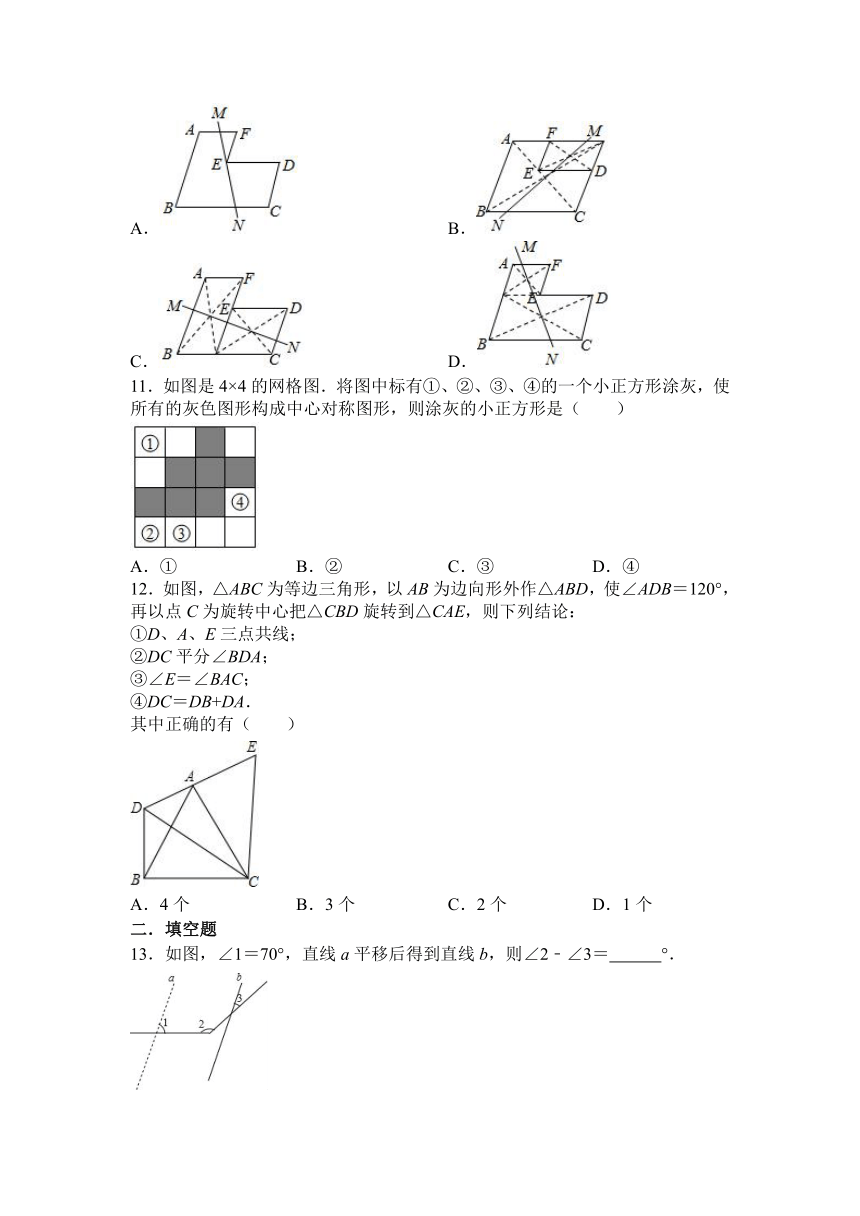
7.在△ABC中,∠ACB=90°,BC=1,AC=3,将△ABC以点C为中心顺时针旋转90°,得到△DEC,连接BE、AD.下列说法错误的是( )
A.S△ABD=6 B.S△ADE=3 C.BE⊥AD D.∠ADE=135°
8.五角星可以看成由一个四边形旋转若干次而生成的,则每次旋转的度数可以是( )
A.36° B.60° C.72° D.90°
9.如图,△ABC绕点A逆时针旋转40°得到△ADE,∠BAC=50°,则∠DAC的度数为( )
A.10° B.15° C.20° D.25°
10.如图,AB∥CD∥EF,AF∥ED∥BC,若画一条直线MN将这个图形分成面积相等的两个部分,则下列画法不一定正确的是( )
A. B.
C. D.
11.如图是4×4的网格图.将图中标有①、②、③、④的一个小正方形涂灰,使所有的灰色图形构成中心对称图形,则涂灰的小正方形是( )
A.① B.② C.③ D.④
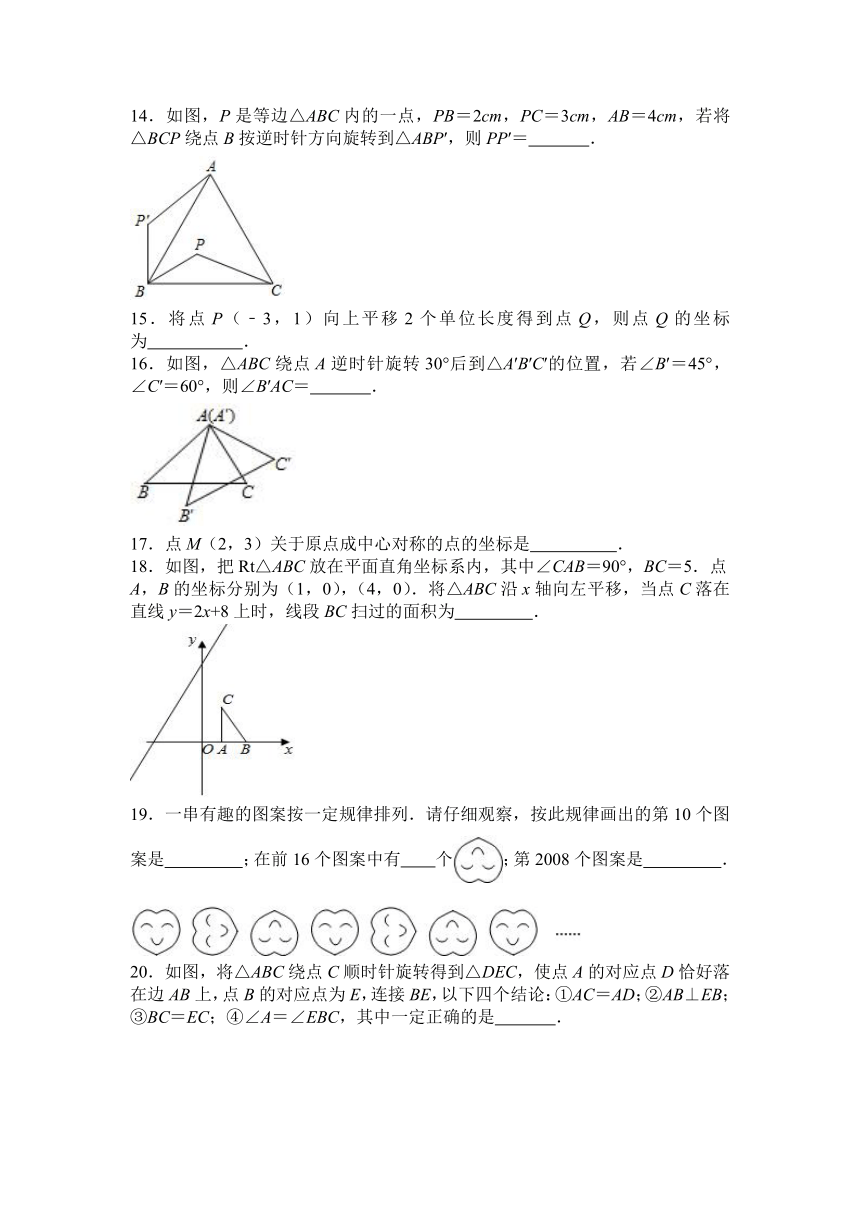
12.如图,△ABC为等边三角形,以AB为边向形外作△ABD,使∠ADB=120°,再以点C为旋转中心把△CBD旋转到△CAE,则下列结论:
①D、A、E三点共线;
②DC平分∠BDA;
③∠E=∠BAC;
④DC=DB+DA.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
二.填空题
13.如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3= °.
14.如图,P是等边△ABC内的一点,PB=2cm,PC=3cm,AB=4cm,若将△BCP绕点B按逆时针方向旋转到△ABP′,则PP′= .
15.将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为 .
16.如图,△ABC绕点A逆时针旋转30°后到△A′B′C′的位置,若∠B′=45°,∠C′=60°,则∠B′AC= .
17.点M(2,3)关于原点成中心对称的点的坐标是 .
18.如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=5.点A,B的坐标分别为(1,0),(4,0).将△ABC沿x轴向左平移,当点C落在直线y=2x+8上时,线段BC扫过的面积为 .
19.一串有趣的图案按一定规律排列.请仔细观察,按此规律画出的第10个图案是 ;在前16个图案中有 个;第2008个图案是 .
20.如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,以下四个结论:①AC=AD;②AB⊥EB;③BC=EC;④∠A=∠EBC,其中一定正确的是 .
三.解答题
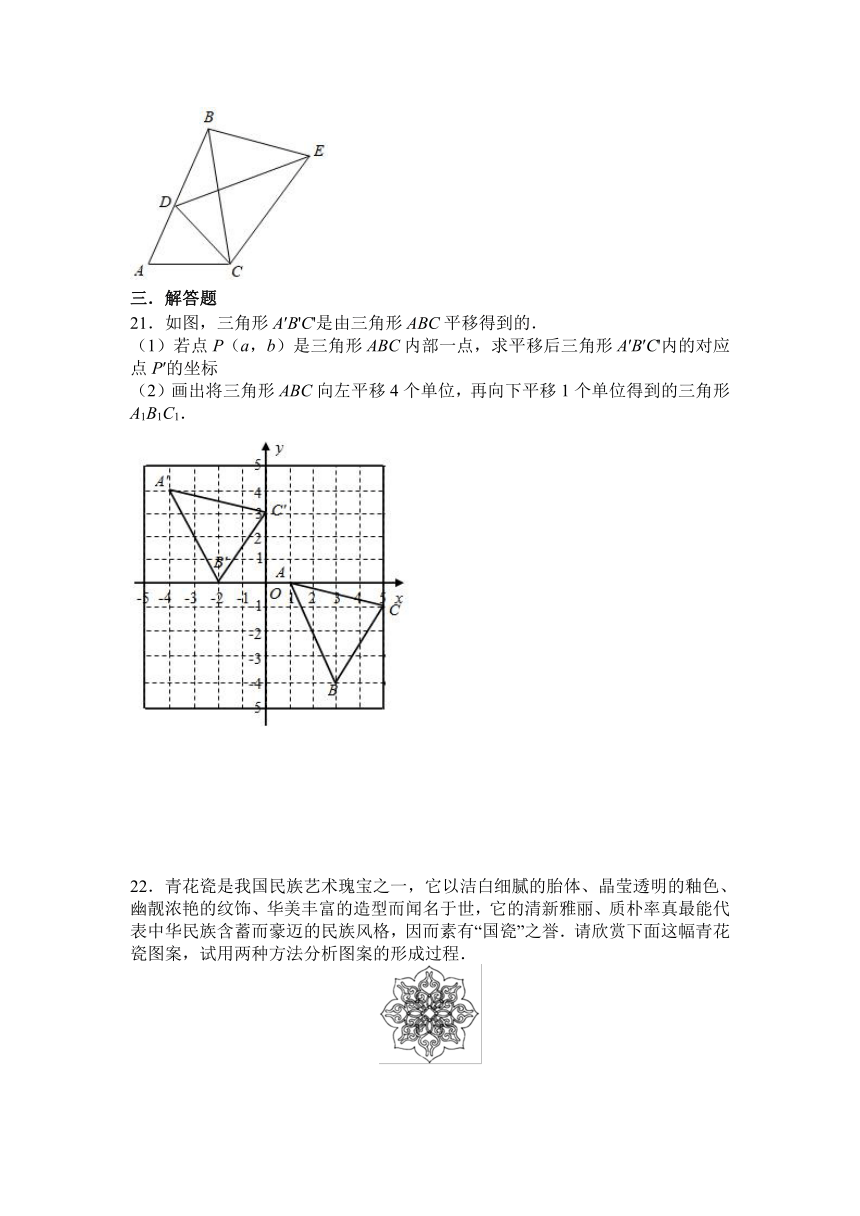
21.如图,三角形A′B'C'是由三角形ABC平移得到的.
(1)若点P(a,b)是三角形ABC内部一点,求平移后三角形A′B′C'内的对应点P′的坐标
(2)画出将三角形ABC向左平移4个单位,再向下平移1个单位得到的三角形A1B1C1.
22.青花瓷是我国民族艺术瑰宝之一,它以洁白细腻的胎体、晶莹透明的釉色、幽靓浓艳的纹饰、华美丰富的造型而闻名于世,它的清新雅丽、质朴率真最能代表中华民族含蓄而豪迈的民族风格,因而素有“国瓷”之誉.请欣赏下面这幅青花瓷图案,试用两种方法分析图案的形成过程.
23.如图所示,有一条等宽的小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,则这条小路的面积是多少?
24.如图,已知△ABC三个顶点的坐标分别是A(﹣3,1),B(﹣1,﹣1),C(2,2).
(1)画出△ABC关于y轴对称的△A1B1C1,并写出点A1,B1,C1的坐标;
(2)画出△ABC绕点B逆时针旋转90°所得到的△A2B2C2,并求出S.
25.如图,△ABO与△CDO关于O点中心对称,点E,F在线段AC上,且AF=CE,求证:FD=BE.
26.在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.
27.如图所示的三种拼块A,B,C,每个拼块都是由一些大小相同、面积为1个单位的小正方形组成,如编号为A的拼块的面积为3个单位.
现用若干个这三种拼块拼正方形,拼图时每种拼块都要用到,且这三种拼块拼图时可平移、旋转,或翻转.
(1)若用1个A种拼块,2个B种拼块,4个C种拼块,则拼出的正方形的面积为 个单位.
(2)在图1和图2中,各画出了一个正方形拼图中1个A种拼块和1个B种拼块,请分别用不同的拼法将图1和图2中的正方形拼图补充完整.要求:所用的A,B,C三种拼块的个数与(1)不同,用实线画出边界线,拼块之间无缝隙,且不重叠.
28.如图,已知△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠EAB=25°,∠F=57°;
(1)请说明∠EAB=∠FAC的理由;
(2)△ABC可以经过图形的变换得到△AEF,请你描述这个变换;
(3)求∠AMB的度数.
北师大版八年级数学下册第三章图形的平移与旋转 同步测试答案
一.选择题
1.一木匠用了最少测量次数就测出了如图(图中所有的角为直角)工件的周长.则他测量的次数为( )
A.6次 B.5次 C.4次 D.3次
解:根据平移不改变线段的长度,
∴可将线段1、线段2、线段3的长度平移到线段6进行测量,线段c、线段b的长度可平移到线段5进行测量,
∴周长可表示为2(线段6的长+线段5的长+线段a的长),
即要得出工件的周长可测量6、5、a的长度,共需测量三次.
故选:D.
2.已知点P关于x轴对称的点的坐标为(2,﹣1),那么点P关于原点对称的点的坐标是( )
A.(1,﹣2) B.(2,1) C.(﹣2,﹣1) D.(﹣2,1)
解:根据轴对称的性质,得P点的坐标是(2,1).
再根据中心对称的性质,得点P关于原点对称的点的坐标是(﹣2,﹣1).
故选:C.
3.在平面直角坐标系中,将点A(x,﹣y)向上平移2个单位长度,再向左平移3个单位长度,得到点A′,则点A′的坐标是( )
A.(x+3,2﹣y) B.(x+3,﹣y﹣2) C.(x﹣3,2﹣y) D.(x﹣3,﹣y﹣2)
3.解:将点A(x,﹣y)向上平移2个单位长度,再向左平移3个单位长度,得到点A'的坐标为(x﹣3,﹣y+2),即(x﹣3,2﹣y),
故选:C.
4.如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
A.20cm B.22cm C.24cm D.26cm
解:∵△ABC沿BC方向平移3cm得到△DEF,
∴DF=AC,AD=CF=3cm,
∵△ABC的周长为20cm,即AB+BC+AC=20cm,
∴AB+BC+CF+DF+AD=AB+BC+AC+AD+CF=20+3+3=26(cm),
即四边形ABFD的周长为26cm.
故选:D.
5.如图,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在A1(﹣2,2)处,则点B的对应点B1的坐标为( )
A.(﹣1,﹣1) B.(﹣1,0) C.(1,0) D.(3,0)
解:观察图像可知,B1(﹣1,0).
故选:B.
6.下列图案中,能用原图平移得到的图案是( )
A. B.
C. D.
解:根据平移得出的图形是;
故选:C.
7.在△ABC中,∠ACB=90°,BC=1,AC=3,将△ABC以点C为中心顺时针旋转90°,得到△DEC,连接BE、AD.下列说法错误的是( )
A.S△ABD=6 B.S△ADE=3 C.BE⊥AD D.∠ADE=135°
7.解:∵将△ABC以点C为中心顺时针旋转90°,得到△DEC,
∴AC=CD=3,BC=CE=1,∠ACD=90°,
∴AE=2,BD=4,∠ADC=∠CAD=∠CBE=∠CEB=45°
∴S△ABD=×BD×AC=6,S△ADE=×AE×CD=3,∠CBE+∠ADC=90°,∠ADE<45°,
∴BE⊥AD.
故选:D.
8.五角星可以看成由一个四边形旋转若干次而生成的,则每次旋转的度数可以是( )
A.36° B.60° C.72° D.90°
解:根据旋转的性质可知,每次旋转的度数可以是360°÷5=72°或72°的倍数.故选C.
9.如图,△ABC绕点A逆时针旋转40°得到△ADE,∠BAC=50°,则∠DAC的度数为( )
A.10° B.15° C.20° D.25°
解:由旋转的性质可知,∠BAD=40°,
∵∠BAC=50°,
∴∠DAC=∠BAC﹣∠BAD=50°﹣40°=10°,
故选:A.
10.如图,AB∥CD∥EF,AF∥ED∥BC,若画一条直线MN将这个图形分成面积相等的两个部分,则下列画法不一定正确的是( )
A. B.
C. D.
解:因为平行四边形是中心对称图形,
所以直线经过两个平行四边形的对角线的交点即可,
观察图象可知,选项B,C,D符合题意,
故选:A.
11.如图是4×4的网格图.将图中标有①、②、③、④的一个小正方形涂灰,使所有的灰色图形构成中心对称图形,则涂灰的小正方形是( )
A.① B.② C.③ D.④
解:如图,观察图象可知,把③涂灰,所有的灰色图形构成中心对称图形.
故选:C.
12.如图,△ABC为等边三角形,以AB为边向形外作△ABD,使∠ADB=120°,再以点C为旋转中心把△CBD旋转到△CAE,则下列结论:
①D、A、E三点共线;
②DC平分∠BDA;
③∠E=∠BAC;
④DC=DB+DA.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
12.解:如图,
①设∠1=x度,则∠2=(60﹣x)度,∠DBC=(x+60)度,故∠4=(x+60)度,
∴∠2+∠3+∠4=60﹣x+60+x+60=180度,
∴D、A、E三点共线;
故①正确;
②∵△BCD绕着点C按顺时针方向旋转60°得到△ACE,
∴CD=CE,∠DCE=60°,
∴△CDE为等边三角形,
∴∠E=60°,
∴∠BDC=∠E=60°,
∴∠CDA=120°﹣60°=60°,
∴DC平分∠BDA;
故②正确;
③∵∠BAC=60°,
∠E=60°,
∴∠E=∠BAC.
故③正确;
④由旋转可知AE=BD,
又∵∠DAE=180°,
∴DE=AE+AD.
∵△CDE为等边三角形,
∴DC=DB+BA.故④正确;
故选:A.
二.填空题
13.如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3= 110 °.
解:延长直线,如图:,
∵直线a平移后得到直线b,
∴a∥b,
∴∠5=180°﹣∠1=180°﹣70°=110°,
∵∠2=∠4+∠5,
∵∠3=∠4,
∴∠2﹣∠3=∠5=110°,
故答案为:110.
14.如图,P是等边△ABC内的一点,PB=2cm,PC=3cm,AB=4cm,若将△BCP绕点B按逆时针方向旋转到△ABP′,则PP′= .
14.解:连接PP',
∵△ABC为等边三角形,
∴∠ABC=60°.
根据旋转的性质,有∠PBP′=∠ABC=60°,BP′=BP,
∴△BPP′是等边三角形,
∴PP′=BP=2cm,
故答案为:2cm.
15.将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为 (﹣3,3) .
解:将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为(﹣3,1+2),即(﹣3,3),
故答案为:(﹣3,3).
16.如图,△ABC绕点A逆时针旋转30°后到△A′B′C′的位置,若∠B′=45°,∠C′=60°,则∠B′AC= 45° .
解:∵∠B′=45°,∠C′=60°,
∴∠BAC=∠B′A′C′=180°﹣45°﹣60°=75°,
∵∠BAB′=30°,
∴∠B′AC=75°﹣30°=45°,
故答案为:45°.
17.点M(2,3)关于原点成中心对称的点的坐标是 (﹣2,﹣3) .
解:点M(2,3)关于原点成中心对称的点的坐标是(﹣2,﹣3).
故答案为:(﹣2,﹣3).
18.如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=5.点A,B的坐标分别为(1,0),(4,0).将△ABC沿x轴向左平移,当点C落在直线y=2x+8上时,线段BC扫过的面积为 12 .
解:在Rt△ABC中,∵∠CAB=90°,BC=5,AB=3,
∴AC==4,
∴C(1,4),
当y=4时,4=2x+8,
x=﹣2,
∴点C向左平移3个单位落在直线y=2x+8上,
∴点B平移的距离为3个单位,
∴线段BC扫过的面积为3×4=12,
故答案为12.
19.一串有趣的图案按一定规律排列.请仔细观察,按此规律画出的第10个图案是 ;在前16个图案中有 5 个;第2008个图案是 .
解:根据分析,知应分别为,5,.
20.如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,以下四个结论:①AC=AD;②AB⊥EB;③BC=EC;④∠A=∠EBC,其中一定正确的是 .
20.解:∵将△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD,BC=CE,AB=DE,故①错误,③正确;
∴∠ACD=∠BCE,
∴∠A=∠ADC=(180°﹣∠ACD),∠CBE=(180°﹣∠BCE),
∴∠A=∠EBC,故④正确;
∵∠A+∠ABC不一定等于90°,
∴∠ABC+∠CBE不一定等于90°,故②错误;
故答案为:③④.
三.解答题
21.如图,三角形A′B'C'是由三角形ABC平移得到的.
(1)若点P(a,b)是三角形ABC内部一点,求平移后三角形A′B′C'内的对应点P′的坐标
(2)画出将三角形ABC向左平移4个单位,再向下平移1个单位得到的三角形A1B1C1.
解:(1)由题意三角形A′B'C'是由三角形ABC向左平移5个单位,向上平移4个单位得到的,
∴点P′的坐标为(a﹣5,b+4);
(2)如图所示,△A1B1C1即为所求.
22.青花瓷是我国民族艺术瑰宝之一,它以洁白细腻的胎体、晶莹透明的釉色、幽靓浓艳的纹饰、华美丰富的造型而闻名于世,它的清新雅丽、质朴率真最能代表中华民族含蓄而豪迈的民族风格,因而素有“国瓷”之誉.请欣赏下面这幅青花瓷图案,试用两种方法分析图案的形成过程.
22.解:(答案不唯一)方案一:以一个花瓣为基本图案,依次旋转45°,90°,135°,180°,225°,270°,315°可得到整个图案;
方案二:以相邻两个花瓣为基本图案,依次旋转90°,180°,270°可得到整个图案.
23.如图所示,有一条等宽的小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,则这条小路的面积是多少?
解;路等宽,得BE=DF,
△ABE≌△CDF,
由勾股定理,得BE==80(m)
S△ABE=60×80÷2=2400(m2)
路的面积=矩形的面积﹣两个三角形的面积
=84×60﹣2400×2
=240(m2).
答:这条小路的面积是240m2.
24.如图,已知△ABC三个顶点的坐标分别是A(﹣3,1),B(﹣1,﹣1),C(2,2).
(1)画出△ABC关于y轴对称的△A1B1C1,并写出点A1,B1,C1的坐标;
(2)画出△ABC绕点B逆时针旋转90°所得到的△A2B2C2,并求出S.
24.解:(1)如图,△A1B1C1为所作;点A1,B1,C1的坐标分别为;(3,1),(1,﹣1),(2,2)
(2)如图,△A2B2C2为所作,S△A2B2C2=2×3﹣×1×3﹣×2×2﹣×1×1=2.
25.如图,△ABO与△CDO关于O点中心对称,点E,F在线段AC上,且AF=CE,求证:FD=BE.
证明:∵△ABO与△CDO关于O点中心对称,
∴BO=DO,AO=CO,
∵AF=CE,
∴AO﹣AF=CO﹣CE,
∴FO=EO,
在△FOD和△EOB中
,
∴△FOD≌△EOB(SAS),
∴DF=BE.
26.在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.
解:(1)在△ABC中,∵∠B+∠ACB=30°,
∴∠BAC=150°,
当△ABC逆时针旋转一定角度后与△ADE重合,
∴旋转中心为点A,∠BAD等于旋转角,即旋转角为150°;
(2)∵△ABC绕点A逆时针旋转150°后与△ADE重合,
∴∠DAE=∠BAC=150°,AB=AD=4,AC=AE,
∴∠BAE=360°﹣150°﹣150°=60°,
∵点C为AD中点,
∴AC=AD=2,
∴AE=2.
27.如图所示的三种拼块A,B,C,每个拼块都是由一些大小相同、面积为1个单位的小正方形组成,如编号为A的拼块的面积为3个单位.
现用若干个这三种拼块拼正方形,拼图时每种拼块都要用到,且这三种拼块拼图时可平移、旋转,或翻转.
(1)若用1个A种拼块,2个B种拼块,4个C种拼块,则拼出的正方形的面积为 25 个单位.
(2)在图1和图2中,各画出了一个正方形拼图中1个A种拼块和1个B种拼块,请分别用不同的拼法将图1和图2中的正方形拼图补充完整.要求:所用的A,B,C三种拼块的个数与(1)不同,用实线画出边界线,拼块之间无缝隙,且不重叠.
解:(1)1个A种拼块,2个B种拼块,4个C种拼块,面积=3+6+16=25,
故答案为:25.
(2)图形如图所示:
28.如图,已知△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠EAB=25°,∠F=57°;
(1)请说明∠EAB=∠FAC的理由;
(2)△ABC可以经过图形的变换得到△AEF,请你描述这个变换;
(3)求∠AMB的度数.
28.解:(1)∵∠B=∠E,AB=AE,BC=EF,
∴△ABC≌△AEF,
∴∠C=∠F,∠BAC=∠EAF,
∴∠BAC﹣∠PAF=∠EAF﹣∠PAF,
∴∠BAE=∠CAF=25°;
(2)通过观察可知△ABC绕点A顺时针旋转25°,可以得到△AEF;
(3)由(1)知∠C=∠F=57°,∠BAE=∠CAF=25°,
∴∠AMB=∠C+∠CAF=57°+25°=82°.
一.选择题
1.一木匠用了最少测量次数就测出了如图(图中所有的角为直角)工件的周长.则他测量的次数为( )
A.6次 B.5次 C.4次 D.3次
2.已知点P关于x轴对称的点的坐标为(2,﹣1),那么点P关于原点对称的点的坐标是( )
A.(1,﹣2) B.(2,1) C.(﹣2,﹣1) D.(﹣2,1)
3.在平面直角坐标系中,将点A(x,﹣y)向上平移2个单位长度,再向左平移3个单位长度,得到点A′,则点A′的坐标是( )
A.(x+3,2﹣y) B.(x+3,﹣y﹣2) C.(x﹣3,2﹣y) D.(x﹣3,﹣y﹣2)
4.如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
A.20cm B.22cm C.24cm D.26cm
5.如图,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在A1(﹣2,2)处,则点B的对应点B1的坐标为( )
A.(﹣1,﹣1) B.(﹣1,0) C.(1,0) D.(3,0)
6.下列图案中,能用原图平移得到的图案是( )
A. B.
C. D.
7.在△ABC中,∠ACB=90°,BC=1,AC=3,将△ABC以点C为中心顺时针旋转90°,得到△DEC,连接BE、AD.下列说法错误的是( )
A.S△ABD=6 B.S△ADE=3 C.BE⊥AD D.∠ADE=135°
8.五角星可以看成由一个四边形旋转若干次而生成的,则每次旋转的度数可以是( )
A.36° B.60° C.72° D.90°
9.如图,△ABC绕点A逆时针旋转40°得到△ADE,∠BAC=50°,则∠DAC的度数为( )
A.10° B.15° C.20° D.25°
10.如图,AB∥CD∥EF,AF∥ED∥BC,若画一条直线MN将这个图形分成面积相等的两个部分,则下列画法不一定正确的是( )
A. B.
C. D.
11.如图是4×4的网格图.将图中标有①、②、③、④的一个小正方形涂灰,使所有的灰色图形构成中心对称图形,则涂灰的小正方形是( )
A.① B.② C.③ D.④
12.如图,△ABC为等边三角形,以AB为边向形外作△ABD,使∠ADB=120°,再以点C为旋转中心把△CBD旋转到△CAE,则下列结论:
①D、A、E三点共线;
②DC平分∠BDA;
③∠E=∠BAC;
④DC=DB+DA.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
二.填空题
13.如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3= °.
14.如图,P是等边△ABC内的一点,PB=2cm,PC=3cm,AB=4cm,若将△BCP绕点B按逆时针方向旋转到△ABP′,则PP′= .
15.将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为 .
16.如图,△ABC绕点A逆时针旋转30°后到△A′B′C′的位置,若∠B′=45°,∠C′=60°,则∠B′AC= .
17.点M(2,3)关于原点成中心对称的点的坐标是 .
18.如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=5.点A,B的坐标分别为(1,0),(4,0).将△ABC沿x轴向左平移,当点C落在直线y=2x+8上时,线段BC扫过的面积为 .
19.一串有趣的图案按一定规律排列.请仔细观察,按此规律画出的第10个图案是 ;在前16个图案中有 个;第2008个图案是 .
20.如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,以下四个结论:①AC=AD;②AB⊥EB;③BC=EC;④∠A=∠EBC,其中一定正确的是 .
三.解答题
21.如图,三角形A′B'C'是由三角形ABC平移得到的.
(1)若点P(a,b)是三角形ABC内部一点,求平移后三角形A′B′C'内的对应点P′的坐标
(2)画出将三角形ABC向左平移4个单位,再向下平移1个单位得到的三角形A1B1C1.
22.青花瓷是我国民族艺术瑰宝之一,它以洁白细腻的胎体、晶莹透明的釉色、幽靓浓艳的纹饰、华美丰富的造型而闻名于世,它的清新雅丽、质朴率真最能代表中华民族含蓄而豪迈的民族风格,因而素有“国瓷”之誉.请欣赏下面这幅青花瓷图案,试用两种方法分析图案的形成过程.
23.如图所示,有一条等宽的小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,则这条小路的面积是多少?
24.如图,已知△ABC三个顶点的坐标分别是A(﹣3,1),B(﹣1,﹣1),C(2,2).
(1)画出△ABC关于y轴对称的△A1B1C1,并写出点A1,B1,C1的坐标;
(2)画出△ABC绕点B逆时针旋转90°所得到的△A2B2C2,并求出S.
25.如图,△ABO与△CDO关于O点中心对称,点E,F在线段AC上,且AF=CE,求证:FD=BE.
26.在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.
27.如图所示的三种拼块A,B,C,每个拼块都是由一些大小相同、面积为1个单位的小正方形组成,如编号为A的拼块的面积为3个单位.
现用若干个这三种拼块拼正方形,拼图时每种拼块都要用到,且这三种拼块拼图时可平移、旋转,或翻转.
(1)若用1个A种拼块,2个B种拼块,4个C种拼块,则拼出的正方形的面积为 个单位.
(2)在图1和图2中,各画出了一个正方形拼图中1个A种拼块和1个B种拼块,请分别用不同的拼法将图1和图2中的正方形拼图补充完整.要求:所用的A,B,C三种拼块的个数与(1)不同,用实线画出边界线,拼块之间无缝隙,且不重叠.
28.如图,已知△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠EAB=25°,∠F=57°;
(1)请说明∠EAB=∠FAC的理由;
(2)△ABC可以经过图形的变换得到△AEF,请你描述这个变换;
(3)求∠AMB的度数.
北师大版八年级数学下册第三章图形的平移与旋转 同步测试答案
一.选择题
1.一木匠用了最少测量次数就测出了如图(图中所有的角为直角)工件的周长.则他测量的次数为( )
A.6次 B.5次 C.4次 D.3次
解:根据平移不改变线段的长度,
∴可将线段1、线段2、线段3的长度平移到线段6进行测量,线段c、线段b的长度可平移到线段5进行测量,
∴周长可表示为2(线段6的长+线段5的长+线段a的长),
即要得出工件的周长可测量6、5、a的长度,共需测量三次.
故选:D.
2.已知点P关于x轴对称的点的坐标为(2,﹣1),那么点P关于原点对称的点的坐标是( )
A.(1,﹣2) B.(2,1) C.(﹣2,﹣1) D.(﹣2,1)
解:根据轴对称的性质,得P点的坐标是(2,1).
再根据中心对称的性质,得点P关于原点对称的点的坐标是(﹣2,﹣1).
故选:C.
3.在平面直角坐标系中,将点A(x,﹣y)向上平移2个单位长度,再向左平移3个单位长度,得到点A′,则点A′的坐标是( )
A.(x+3,2﹣y) B.(x+3,﹣y﹣2) C.(x﹣3,2﹣y) D.(x﹣3,﹣y﹣2)
3.解:将点A(x,﹣y)向上平移2个单位长度,再向左平移3个单位长度,得到点A'的坐标为(x﹣3,﹣y+2),即(x﹣3,2﹣y),
故选:C.
4.如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
A.20cm B.22cm C.24cm D.26cm
解:∵△ABC沿BC方向平移3cm得到△DEF,
∴DF=AC,AD=CF=3cm,
∵△ABC的周长为20cm,即AB+BC+AC=20cm,
∴AB+BC+CF+DF+AD=AB+BC+AC+AD+CF=20+3+3=26(cm),
即四边形ABFD的周长为26cm.
故选:D.
5.如图,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在A1(﹣2,2)处,则点B的对应点B1的坐标为( )
A.(﹣1,﹣1) B.(﹣1,0) C.(1,0) D.(3,0)
解:观察图像可知,B1(﹣1,0).
故选:B.
6.下列图案中,能用原图平移得到的图案是( )
A. B.
C. D.
解:根据平移得出的图形是;
故选:C.
7.在△ABC中,∠ACB=90°,BC=1,AC=3,将△ABC以点C为中心顺时针旋转90°,得到△DEC,连接BE、AD.下列说法错误的是( )
A.S△ABD=6 B.S△ADE=3 C.BE⊥AD D.∠ADE=135°
7.解:∵将△ABC以点C为中心顺时针旋转90°,得到△DEC,
∴AC=CD=3,BC=CE=1,∠ACD=90°,
∴AE=2,BD=4,∠ADC=∠CAD=∠CBE=∠CEB=45°
∴S△ABD=×BD×AC=6,S△ADE=×AE×CD=3,∠CBE+∠ADC=90°,∠ADE<45°,
∴BE⊥AD.
故选:D.
8.五角星可以看成由一个四边形旋转若干次而生成的,则每次旋转的度数可以是( )
A.36° B.60° C.72° D.90°
解:根据旋转的性质可知,每次旋转的度数可以是360°÷5=72°或72°的倍数.故选C.
9.如图,△ABC绕点A逆时针旋转40°得到△ADE,∠BAC=50°,则∠DAC的度数为( )
A.10° B.15° C.20° D.25°
解:由旋转的性质可知,∠BAD=40°,
∵∠BAC=50°,
∴∠DAC=∠BAC﹣∠BAD=50°﹣40°=10°,
故选:A.
10.如图,AB∥CD∥EF,AF∥ED∥BC,若画一条直线MN将这个图形分成面积相等的两个部分,则下列画法不一定正确的是( )
A. B.
C. D.
解:因为平行四边形是中心对称图形,
所以直线经过两个平行四边形的对角线的交点即可,
观察图象可知,选项B,C,D符合题意,
故选:A.
11.如图是4×4的网格图.将图中标有①、②、③、④的一个小正方形涂灰,使所有的灰色图形构成中心对称图形,则涂灰的小正方形是( )
A.① B.② C.③ D.④
解:如图,观察图象可知,把③涂灰,所有的灰色图形构成中心对称图形.
故选:C.
12.如图,△ABC为等边三角形,以AB为边向形外作△ABD,使∠ADB=120°,再以点C为旋转中心把△CBD旋转到△CAE,则下列结论:
①D、A、E三点共线;
②DC平分∠BDA;
③∠E=∠BAC;
④DC=DB+DA.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
12.解:如图,
①设∠1=x度,则∠2=(60﹣x)度,∠DBC=(x+60)度,故∠4=(x+60)度,
∴∠2+∠3+∠4=60﹣x+60+x+60=180度,
∴D、A、E三点共线;
故①正确;
②∵△BCD绕着点C按顺时针方向旋转60°得到△ACE,
∴CD=CE,∠DCE=60°,
∴△CDE为等边三角形,
∴∠E=60°,
∴∠BDC=∠E=60°,
∴∠CDA=120°﹣60°=60°,
∴DC平分∠BDA;
故②正确;
③∵∠BAC=60°,
∠E=60°,
∴∠E=∠BAC.
故③正确;
④由旋转可知AE=BD,
又∵∠DAE=180°,
∴DE=AE+AD.
∵△CDE为等边三角形,
∴DC=DB+BA.故④正确;
故选:A.
二.填空题
13.如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3= 110 °.
解:延长直线,如图:,
∵直线a平移后得到直线b,
∴a∥b,
∴∠5=180°﹣∠1=180°﹣70°=110°,
∵∠2=∠4+∠5,
∵∠3=∠4,
∴∠2﹣∠3=∠5=110°,
故答案为:110.
14.如图,P是等边△ABC内的一点,PB=2cm,PC=3cm,AB=4cm,若将△BCP绕点B按逆时针方向旋转到△ABP′,则PP′= .
14.解:连接PP',
∵△ABC为等边三角形,
∴∠ABC=60°.
根据旋转的性质,有∠PBP′=∠ABC=60°,BP′=BP,
∴△BPP′是等边三角形,
∴PP′=BP=2cm,
故答案为:2cm.
15.将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为 (﹣3,3) .
解:将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为(﹣3,1+2),即(﹣3,3),
故答案为:(﹣3,3).
16.如图,△ABC绕点A逆时针旋转30°后到△A′B′C′的位置,若∠B′=45°,∠C′=60°,则∠B′AC= 45° .
解:∵∠B′=45°,∠C′=60°,
∴∠BAC=∠B′A′C′=180°﹣45°﹣60°=75°,
∵∠BAB′=30°,
∴∠B′AC=75°﹣30°=45°,
故答案为:45°.
17.点M(2,3)关于原点成中心对称的点的坐标是 (﹣2,﹣3) .
解:点M(2,3)关于原点成中心对称的点的坐标是(﹣2,﹣3).
故答案为:(﹣2,﹣3).
18.如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=5.点A,B的坐标分别为(1,0),(4,0).将△ABC沿x轴向左平移,当点C落在直线y=2x+8上时,线段BC扫过的面积为 12 .
解:在Rt△ABC中,∵∠CAB=90°,BC=5,AB=3,
∴AC==4,
∴C(1,4),
当y=4时,4=2x+8,
x=﹣2,
∴点C向左平移3个单位落在直线y=2x+8上,
∴点B平移的距离为3个单位,
∴线段BC扫过的面积为3×4=12,
故答案为12.
19.一串有趣的图案按一定规律排列.请仔细观察,按此规律画出的第10个图案是 ;在前16个图案中有 5 个;第2008个图案是 .
解:根据分析,知应分别为,5,.
20.如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,以下四个结论:①AC=AD;②AB⊥EB;③BC=EC;④∠A=∠EBC,其中一定正确的是 .
20.解:∵将△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD,BC=CE,AB=DE,故①错误,③正确;
∴∠ACD=∠BCE,
∴∠A=∠ADC=(180°﹣∠ACD),∠CBE=(180°﹣∠BCE),
∴∠A=∠EBC,故④正确;
∵∠A+∠ABC不一定等于90°,
∴∠ABC+∠CBE不一定等于90°,故②错误;
故答案为:③④.
三.解答题
21.如图,三角形A′B'C'是由三角形ABC平移得到的.
(1)若点P(a,b)是三角形ABC内部一点,求平移后三角形A′B′C'内的对应点P′的坐标
(2)画出将三角形ABC向左平移4个单位,再向下平移1个单位得到的三角形A1B1C1.
解:(1)由题意三角形A′B'C'是由三角形ABC向左平移5个单位,向上平移4个单位得到的,
∴点P′的坐标为(a﹣5,b+4);
(2)如图所示,△A1B1C1即为所求.
22.青花瓷是我国民族艺术瑰宝之一,它以洁白细腻的胎体、晶莹透明的釉色、幽靓浓艳的纹饰、华美丰富的造型而闻名于世,它的清新雅丽、质朴率真最能代表中华民族含蓄而豪迈的民族风格,因而素有“国瓷”之誉.请欣赏下面这幅青花瓷图案,试用两种方法分析图案的形成过程.
22.解:(答案不唯一)方案一:以一个花瓣为基本图案,依次旋转45°,90°,135°,180°,225°,270°,315°可得到整个图案;
方案二:以相邻两个花瓣为基本图案,依次旋转90°,180°,270°可得到整个图案.
23.如图所示,有一条等宽的小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,则这条小路的面积是多少?
解;路等宽,得BE=DF,
△ABE≌△CDF,
由勾股定理,得BE==80(m)
S△ABE=60×80÷2=2400(m2)
路的面积=矩形的面积﹣两个三角形的面积
=84×60﹣2400×2
=240(m2).
答:这条小路的面积是240m2.
24.如图,已知△ABC三个顶点的坐标分别是A(﹣3,1),B(﹣1,﹣1),C(2,2).
(1)画出△ABC关于y轴对称的△A1B1C1,并写出点A1,B1,C1的坐标;
(2)画出△ABC绕点B逆时针旋转90°所得到的△A2B2C2,并求出S.
24.解:(1)如图,△A1B1C1为所作;点A1,B1,C1的坐标分别为;(3,1),(1,﹣1),(2,2)
(2)如图,△A2B2C2为所作,S△A2B2C2=2×3﹣×1×3﹣×2×2﹣×1×1=2.
25.如图,△ABO与△CDO关于O点中心对称,点E,F在线段AC上,且AF=CE,求证:FD=BE.
证明:∵△ABO与△CDO关于O点中心对称,
∴BO=DO,AO=CO,
∵AF=CE,
∴AO﹣AF=CO﹣CE,
∴FO=EO,
在△FOD和△EOB中
,
∴△FOD≌△EOB(SAS),
∴DF=BE.
26.在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.
解:(1)在△ABC中,∵∠B+∠ACB=30°,
∴∠BAC=150°,
当△ABC逆时针旋转一定角度后与△ADE重合,
∴旋转中心为点A,∠BAD等于旋转角,即旋转角为150°;
(2)∵△ABC绕点A逆时针旋转150°后与△ADE重合,
∴∠DAE=∠BAC=150°,AB=AD=4,AC=AE,
∴∠BAE=360°﹣150°﹣150°=60°,
∵点C为AD中点,
∴AC=AD=2,
∴AE=2.
27.如图所示的三种拼块A,B,C,每个拼块都是由一些大小相同、面积为1个单位的小正方形组成,如编号为A的拼块的面积为3个单位.
现用若干个这三种拼块拼正方形,拼图时每种拼块都要用到,且这三种拼块拼图时可平移、旋转,或翻转.
(1)若用1个A种拼块,2个B种拼块,4个C种拼块,则拼出的正方形的面积为 25 个单位.
(2)在图1和图2中,各画出了一个正方形拼图中1个A种拼块和1个B种拼块,请分别用不同的拼法将图1和图2中的正方形拼图补充完整.要求:所用的A,B,C三种拼块的个数与(1)不同,用实线画出边界线,拼块之间无缝隙,且不重叠.
解:(1)1个A种拼块,2个B种拼块,4个C种拼块,面积=3+6+16=25,
故答案为:25.
(2)图形如图所示:
28.如图,已知△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠EAB=25°,∠F=57°;
(1)请说明∠EAB=∠FAC的理由;
(2)△ABC可以经过图形的变换得到△AEF,请你描述这个变换;
(3)求∠AMB的度数.
28.解:(1)∵∠B=∠E,AB=AE,BC=EF,
∴△ABC≌△AEF,
∴∠C=∠F,∠BAC=∠EAF,
∴∠BAC﹣∠PAF=∠EAF﹣∠PAF,
∴∠BAE=∠CAF=25°;
(2)通过观察可知△ABC绕点A顺时针旋转25°,可以得到△AEF;
(3)由(1)知∠C=∠F=57°,∠BAE=∠CAF=25°,
∴∠AMB=∠C+∠CAF=57°+25°=82°.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
