五一假期专题复习提升训练卷1(第9章中心对称图形-平行四边形)-2020-2021学年苏科版八年级数学下册(Word版含解析)
文档属性
| 名称 | 五一假期专题复习提升训练卷1(第9章中心对称图形-平行四边形)-2020-2021学年苏科版八年级数学下册(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 981.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-30 11:57:20 | ||
图片预览

文档简介
五一假期专题复习提升训练卷1(9章中心对称图形-平行四边形)
-苏科版八年级数学下册
一、选择题
1、下列图案中,是中心对称图形的是( )
A. B. C. D.
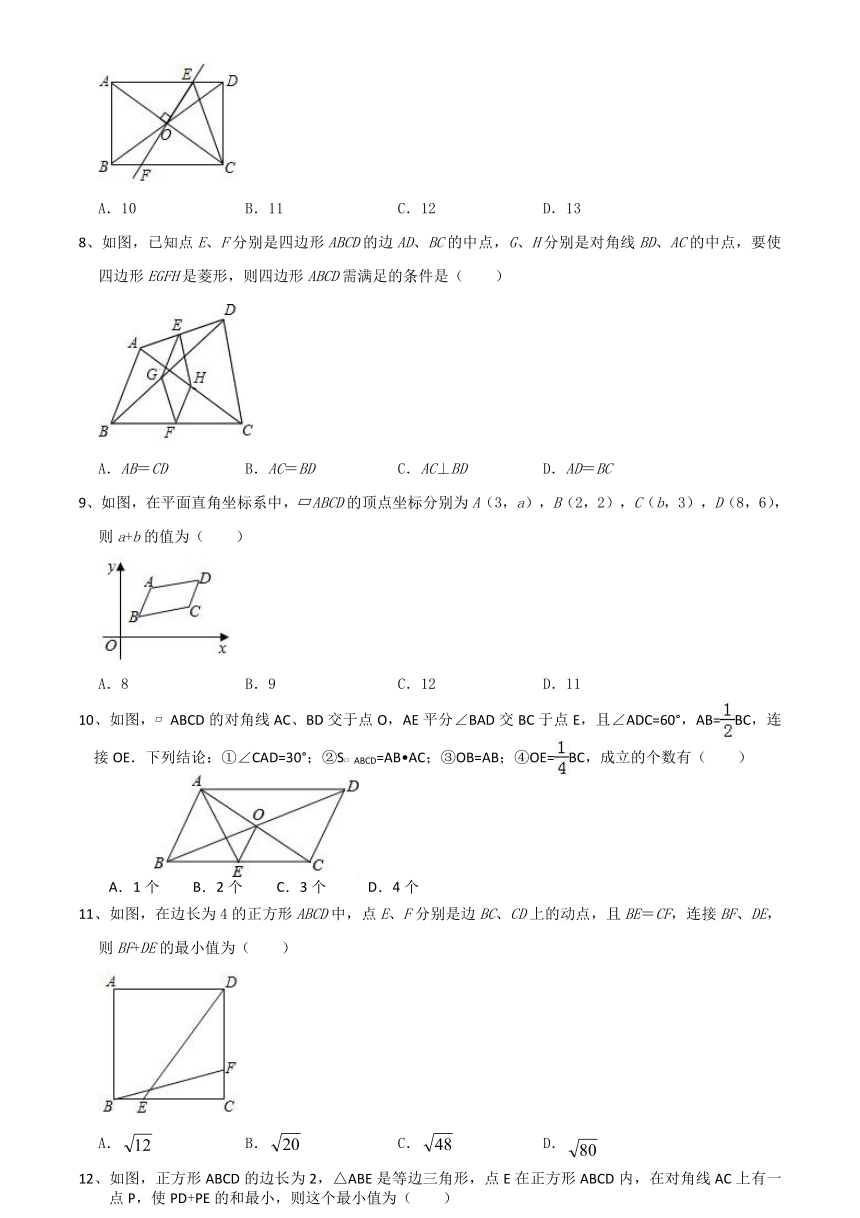
2、如图,在Rt△ABC中,∠C=90°,把△ABC绕AC边的中点M旋转后得△DEF,若直角顶点F恰好落在AB边上,且DE边交AB边于点G,若AC=4,BC=3,则AG的长为( )
A. B. C. D.1
3、在下列性质中,平行四边形不一定具有的性质是( )
A.邻角互补 B.对角相等
C.内角和为360° D.对角互补
4、下列四个选项中,能判断四边形ABCD是平行四边形的是( )
A.AB=CD,AC=BD B.∠A=∠B,∠B=∠C
C.AB=CD,AD∥BC D.AB∥CD,∠A=∠C
5、菱形的对角线不具备的性质是( )
A.对角线互相平分 B.对角线一定相等
C.对角线一定垂直 D.对角线平分一组对角
6、如图所示,在矩形ABCD中,E为AD上一点,EF⊥CE交AB于点F,若DE=2,矩形ABCD的周长为16,且CE=EF,求AE的长( )
A.2 B.3 C.4 D.6
7、如图,在矩形ABCD中,AB=4,BC=6,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,连接CE,△DEC的周长为( )
A.10 B.11 C.12 D.13
8、如图,已知点E、F分别是四边形ABCD的边AD、BC的中点,G、H分别是对角线BD、AC的中点,要使四边形EGFH是菱形,则四边形ABCD需满足的条件是( )
A.AB=CD B.AC=BD C.AC⊥BD D.AD=BC
9、如图,在平面直角坐标系中,?ABCD的顶点坐标分别为A(3,a),B(2,2),C(b,3),D(8,6),则a+b的值为( )
A.8 B.9 C.12 D.11
10、如图,?ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB?AC;③OB=AB;④OE=BC,成立的个数有( )
A.1个 B.2个 C.3个 D.4个
11、如图,在边长为4的正方形ABCD中,点E、F分别是边BC、CD上的动点,且BE=CF,连接BF、DE,则BF+DE的最小值为( )
A. B. C. D.
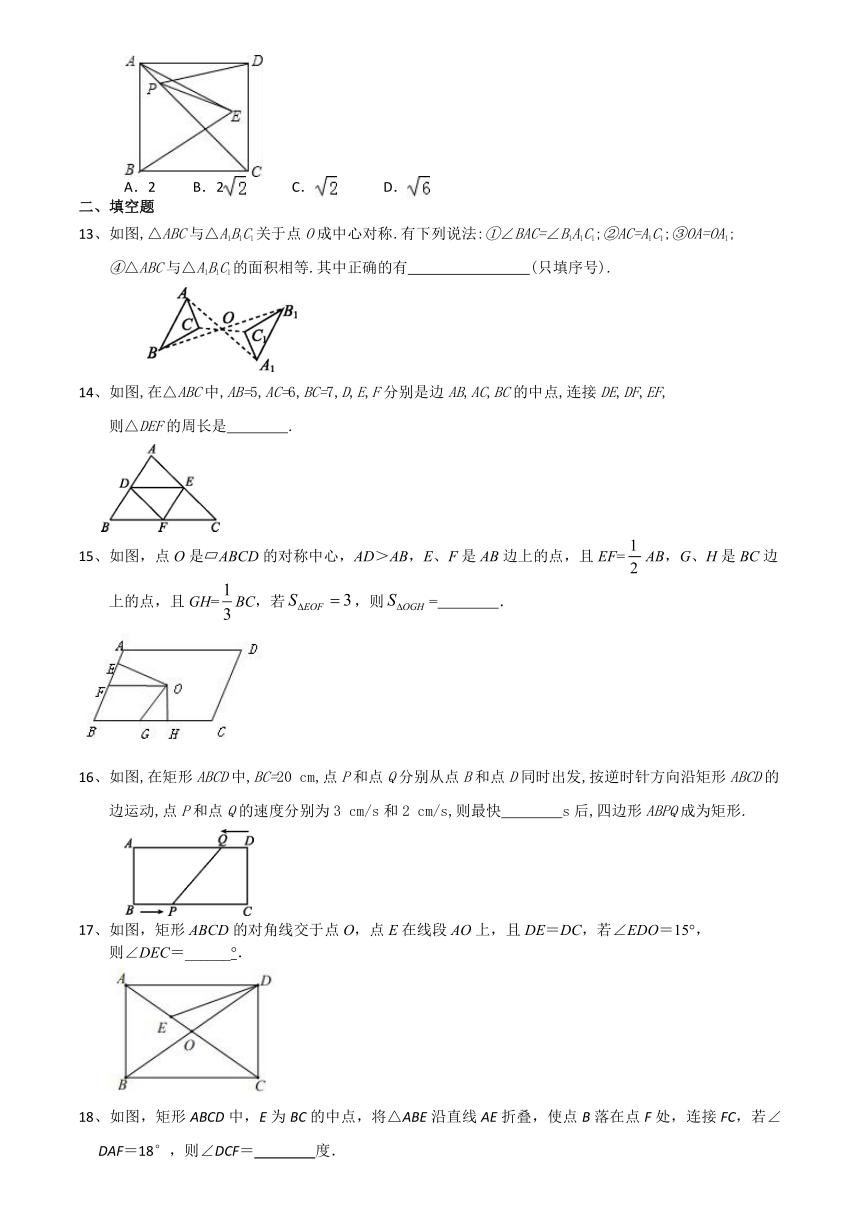
12、如图,正方形ABCD的边长为2,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A.2 B.2 C. D.
二、填空题
13、如图,△ABC与△A1B1C1关于点O成中心对称.有下列说法:①∠BAC=∠B1A1C1;②AC=A1C1;③OA=OA1;
④△ABC与△A1B1C1的面积相等.其中正确的有 (只填序号).?
14、如图,在△ABC中,AB=5,AC=6,BC=7,D,E,F分别是边AB,AC,BC的中点,连接DE,DF,EF,
则△DEF的周长是 .?
15、如图,点O是?ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB,G、H是BC边上的点,且GH=BC,若,则= .
16、如图,在矩形ABCD中,BC=20 cm,点P和点Q分别从点B和点D同时出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3 cm/s和2 cm/s,则最快 s后,四边形ABPQ成为矩形.?
17、如图,矩形ABCD的对角线交于点O,点E在线段AO上,且DE=DC,若∠EDO=15°,
则∠DEC=______°.
18、如图,矩形ABCD中,E为BC的中点,将△ABE沿直线AE折叠,使点B落在点F处,连接FC,若∠DAF=18°,则∠DCF= 度.
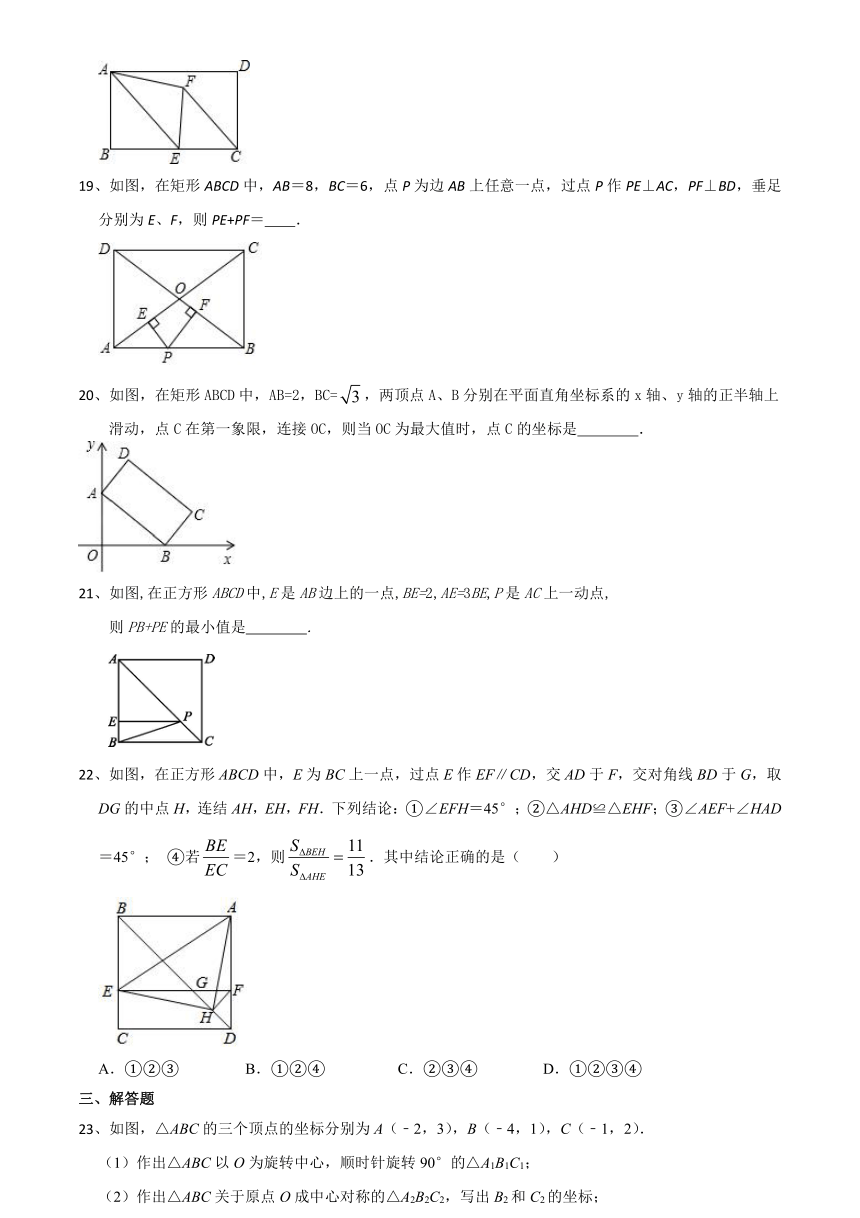
19、如图,在矩形ABCD中,AB=8,BC=6,点P为边AB上任意一点,过点P作PE⊥AC,PF⊥BD,垂足分别为E、F,则PE+PF= .
20、如图,在矩形ABCD中,AB=2,BC=,两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动,点C在第一象限,连接OC,则当OC为最大值时,点C的坐标是 .
21、如图,在正方形ABCD中,E是AB边上的一点,BE=2,AE=3BE,P是AC上一动点,
则PB+PE的最小值是 .?
22、如图,在正方形ABCD中,E为BC上一点,过点E作EF∥CD,交AD于F,交对角线BD于G,取DG的中点H,连结AH,EH,FH.下列结论:①∠EFH=45°;②△AHD≌△EHF;③∠AEF+∠HAD=45°; ④若=2,则.其中结论正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
三、解答题
23、如图,△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣4,1),C(﹣1,2).
(1)作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1;
(2)作出△ABC关于原点O成中心对称的△A2B2C2,写出B2和C2的坐标;
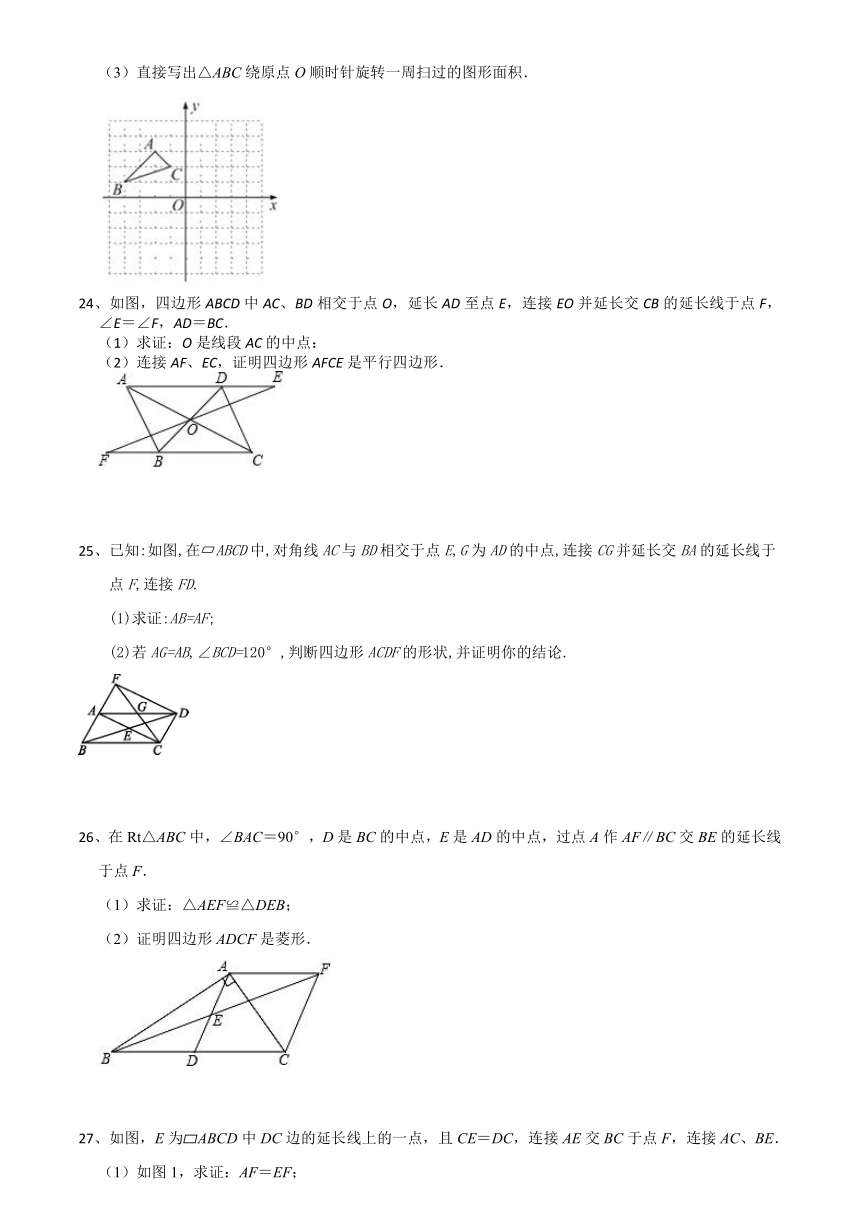
(3)直接写出△ABC绕原点O顺时针旋转一周扫过的图形面积.
24、如图,四边形ABCD中AC、BD相交于点O,延长AD至点E,连接EO并延长交CB的延长线于点F,∠E=∠F,AD=BC.
(1)求证:O是线段AC的中点:
(2)连接AF、EC,证明四边形AFCE是平行四边形.
25、已知:如图,在?ABCD中,对角线AC与BD相交于点E,G为AD的中点,连接CG并延长交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
26、在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形.
27、如图,E为?ABCD中DC边的延长线上的一点,且CE=DC,连接AE交BC于点F,连接AC、BE.
(1)如图1,求证:AF=EF;
(2)连接BD交AC于点O,连接OF并延长交BE于点G,直接写出图中所有长度是OF二倍的线段.
28、如图(a),在矩形纸片ABCD中,AB=3 cm,AD=5 cm,折叠纸片使点B落在边AD上的点E处,折痕为PQ,过点E作EF∥AB交PQ于点F,连接BF.
(1)求证:四边形BFEP为菱形.
(2)当点E在AD边上移动时,折痕的端点P,Q也随之移动.
①当点Q与点C重合时,如图(b),求菱形BFEP的边长;
②若限定点P,Q分别在边BA,BC上移动,求点E在边AD上移动的最大距离.
29、如图①所示,已知A、B为直线l上两点,点C为直线上方一动点,连接AC、BC,分别以AC、BC
为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1⊥l于点D1,过点E作EE1⊥l于点E1.
(1)如图②,当点E恰好在直线l上时(此时E1与E重合),试说明DD1=AB;
(2)在图①中,当D、E两点都在直线l的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并
说明理由;
(3)如图③,当点E在直线l的下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系.
图① 图② 图③
30、如图,已知平行四边形中,对角线,交于点,是延长线上的点,且 是等边三角形.
(1)求证:四边形是菱形;
(2)若,求证:四边形是正方形.
五一假期专题复习提升训练卷1(9章中心对称图形-平行四边形)
-苏科版八年级数学下册(解析)
一、选择题
1、下列图案中,是中心对称图形的是( )
A. B. C. D.
解:A、是中心对称图形,故本选项符合题意;
B、不是中心对称图形,故本选项不合题意;
C、不是中心对称图形,故本选项不合题意;
D、不是中心对称图形,故本选项不合题意.
故选:A.
2、如图,在Rt△ABC中,∠C=90°,把△ABC绕AC边的中点M旋转后得△DEF,若直角顶点F恰好落在AB边上,且DE边交AB边于点G,若AC=4,BC=3,则AG的长为( )
A. B. C. D.1
解:∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB=5,
∵点M是AC边的中点,∴CM=AM=AC=2,
∵把△ABC绕AC边的中点M旋转后得△DEF,若直角顶点F恰好落在AB边上,
∴CM=FM=2,∠D=∠A,∠C=∠DFE,AB=DE,∴AM=MF,∴∠A=∠AFM,
∴∠D=∠AFD,∴DG=FG,
∵∠D+∠E=∠DFG+∠GFE=90°,
∴∠E=∠EFG,∴EG=FG,∴FG=DE=,
∵AM=CM=FM=AC,∴∠AFC=90°,∴CF==,
∴AF==,∴AG=AF﹣FG=﹣=,
故选:A.
3、在下列性质中,平行四边形不一定具有的性质是( )
A.邻角互补 B.对角相等
C.内角和为360° D.对角互补
解:平行四边形邻角互补,对角相等,内角和为360°,不具备的性质是对角互补,
故选:D.
4、下列四个选项中,能判断四边形ABCD是平行四边形的是( )
A.AB=CD,AC=BD B.∠A=∠B,∠B=∠C
C.AB=CD,AD∥BC D.AB∥CD,∠A=∠C
解:A、AB=CD,AC=BD不能判定四边形ABCD是平行四边形,故此选项错误;
B、∠A=∠B,∠B=∠C不能判定四边形ABCD是平行四边形,故此选项错误;
C、AB=CD,AD∥BC不能判定四边形ABCD是平行四边形,故此选项错误;
D、∵AB∥CD,∴∠A+∠D=∠B+∠C=180°,
∵∠A=∠C,∴∠B=∠D,∴四边形ABCD是平行四边形,故此选项正确;
故选:D.
5、菱形的对角线不具备的性质是( )
A.对角线互相平分 B.对角线一定相等
C.对角线一定垂直 D.对角线平分一组对角
解:菱形的性质:四条边都相等,对角线互相垂直平分,是轴对称图形,并且每一条对角线平分一组对角;
菱形的对角线不一定相等;
故选:B.
6、如图所示,在矩形ABCD中,E为AD上一点,EF⊥CE交AB于点F,若DE=2,矩形ABCD的周长为16,且CE=EF,求AE的长( )
A.2 B.3 C.4 D.6
解:∵四边形ABCD为矩形,∴∠A=∠D=90°,
∵EF⊥CE,∴∠CEF=90°,∴∠CED+∠AEF=90°,
∵∠CED+∠DCE=90°,∴∠DCE=∠AEF,
在△AEF和△DCE中,,∴△AEF≌△DCE(AAS),∴AE=DC,
由题意可知:2(AE+DE+CD)=16,DE=2,∴2AE=6,∴AE=3;
故选:B.
7、如图,在矩形ABCD中,AB=4,BC=6,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,连接CE,△DEC的周长为( )
A.10 B.11 C.12 D.13
解:设DE=x,则AE=6﹣x,
∵四边形ABCD是矩形,∴∠ADC=90°,DC=AB=4,AD=BC=6,AO=OC,
∵EF⊥AC,AO=OC,∴AE=CE=6﹣x,
在Rt△DEC中,由勾股定理得:DE2+DC2=EC2,
即x2+42=(6﹣x)2,解得:x=,
即DE=,CE=AE=6﹣=,
∴△DEC的周长为DE+CE+DC=++4=10,
故选:A.
8、如图,已知点E、F分别是四边形ABCD的边AD、BC的中点,G、H分别是对角线BD、AC的中点,要使四边形EGFH是菱形,则四边形ABCD需满足的条件是( )
A.AB=CD B.AC=BD C.AC⊥BD D.AD=BC
解:∵点E、F分别是四边形ABCD的边AD、BC的中点,G、H分别是对角线BD、AC的中点,
∴EG=FH=AB,EH=FG=CD,
∵当EG=FH=GF=EH时,四边形EGFH是菱形,
∴当AB=CD时,四边形EGFH是菱形.
故选:A.
9、如图,在平面直角坐标系中,?ABCD的顶点坐标分别为A(3,a),B(2,2),C(b,3),D(8,6),则a+b的值为( )
A.8 B.9 C.12 D.11
解:如图,连接AC、BD交于点O′.
∵四边形ABCD是平行四边形,∴AO′=O′C,BO′=O′D,
∵A(3,a),B(2,2),C(b,3),D(8,6),
∴=,=,
∴a=5,b=7,∴a+b=12,
故选:C.
10、如图,?ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB?AC;③OB=AB;④OE=BC,成立的个数有( )
A.1个 B.2个 C.3个 D.4个
【考点】平行四边形的性质;等腰三角形的判定与性质;等边三角形的判定与性质;含30度角的直角三角形.
【分析】由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据AE平分∠BAD,得到∠BAE=∠EAD=60°推出△ABE是等边三角形,由于AB=BC,得到AE=BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;由于AC⊥AB,得到S?ABCD=AB?AC,故②正确,根据AB=BC,OB=BD,且BD>BC,得到AB≠OB,故③错误;根据三角形的中位线定理得到OE=AB,于是得到OE=BC,故④正确.
【解答】解:∵四边形ABCD是平行四边形,∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,∴∠BAE=∠EAD=60°∴△ABE是等边三角形,∴AE=AB=BE,
∵AB=BC,∴AE=BC,∴∠BAC=90°,∴∠CAD=30°,故①正确;
∵AC⊥AB,∴S?ABCD=AB?AC,故②正确,
∵AB=BC,OB=BD,∵BD>BC,∴AB≠OB,故③错误;
∵CE=BE,CO=OA,∴OE=AB,∴OE=BC,故④正确.
故选:C.
11、如图,在边长为4的正方形ABCD中,点E、F分别是边BC、CD上的动点,且BE=CF,连接BF、DE,则BF+DE的最小值为( )
A. B. C. D.
解:连接AE,如图1,∵四边形ABCD是正方形,∴AB=BC,∠ABE=∠BCF=90°.
又BE=CF,∴△ABE≌△BCF(SAS).∴AE=BF. 所以BF+DE最小值等于AE+DE最小值.
作点A关于BC的对称点H点,如图2,连接BH,则A、B、H三点共线,
连接DH,DH与BC的交点即为所求的E点.根据对称性可知AE=HE, 所以AE+DE=DH.
在Rt△ADH中,DH=,
∴BF+DE最小值为.
故选:D.
12、如图,正方形ABCD的边长为2,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A.2 B.2 C. D.
【考点】轴对称﹣最短路线问题;正方形的性质.
【分析】由于点B与D关于AC对称,所以连接BE,与AC的交点即为P点.此时PD+PE=BE最小,而BE是等边△ABE的边,BE=AB,由正方形ABCD的面积为4,可求出AB的长,从而得出结果.
【解答】解:连接BD,与AC交于点F.
∵点B与D关于AC对称,∴PD=PB,∴PD+PE=PB+PE=BE最小.
∵正方形ABCD的边长为2,∴AB=2.
又∵△ABE是等边三角形,∴BE=AB=2.∴所求最小值为2.
故选:A.
二、填空题
13、如图,△ABC与△A1B1C1关于点O成中心对称.有下列说法:①∠BAC=∠B1A1C1;②AC=A1C1;③OA=OA1;
④△ABC与△A1B1C1的面积相等.其中正确的有 (只填序号).?
[答案] ①②③④
[解析] 中心对称的两个图形全等,所以∠BAC=∠B1A1C1,AC=A1C1,△ABC与△A1B1C1的面积相等,故①②④正确;对称点到对称中心的距离相等,故③正确.故答案为①②③④.
14、如图,在△ABC中,AB=5,AC=6,BC=7,D,E,F分别是边AB,AC,BC的中点,连接DE,DF,EF,
则△DEF的周长是 .?
[答案] 9
[解析] ∵D,E,F分别是边AB,AC,BC的中点,∴DE=BC=3.5,DF=AC=3,EF=AB=2.5,
∴△DEF的周长=DE+DF+EF=9.
故答案为9.
15、如图,点O是?ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB,G、H是BC边上的点,且GH=BC,若,则= .
【答案】2
【解析】解:连接AC、BD,如图,
∵点O是?ABCD的对称中心,∴AC、BD交于点O,∴S△AOB=S△BOC,
∵EF=AB,∴S△EOF=S△AOB,
∵GH=BC,∴S△OGH=S△BOC,
∴S△EOF:S△OGH=3:2,
∵,∴=2.
故答案为:2.
16、如图,在矩形ABCD中,BC=20 cm,点P和点Q分别从点B和点D同时出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3 cm/s和2 cm/s,则最快 s后,四边形ABPQ成为矩形.?
[答案] 4
[解析] 设最快x s后,四边形ABPQ成为矩形,由BP=AQ,得3x=20-2x.
解得x=4.
故答案为4.
17、如图,矩形ABCD的对角线交于点O,点E在线段AO上,且DE=DC,若∠EDO=15°,
则∠DEC=______°.
【答案】55
【解析】解:设∠DEC=x,
∵DE=DC,∴∠DCE=x,
∵四边形ABCD为矩形,∴∠ODC=∠DCE=x,
∴∠DOE=∠OCD+∠ODC=2x,
∵△DOE内角和为180°,∴,解得:,即∠DEC=,
故答案为:55.
18、如图,矩形ABCD中,E为BC的中点,将△ABE沿直线AE折叠,使点B落在点F处,连接FC,若∠DAF=18°,则∠DCF= 度.
【分析】由折叠的性质得:FE=BE,∠FAE=∠BAE,∠AEB=∠AEF,求出∠BAE=∠FAE=36°,由直角三角形的性质得出∠AEF=∠AEB=54°,求出∠CEF=72°,求出FE=CE,由等腰三角形的性质求出∠ECF=54°,即可得出∠DCF的度数.
【解析】∵四边形ABCD是矩形,∴∠BAD=∠B=∠BCD=90°,
由折叠的性质得:FE=BE,∠FAE=∠BAE,∠AEB=∠AEF,
∵∠DAF=18°,∴∠BAE=∠FAE=(90°﹣18°)=36°,
∴∠AEF=∠AEB=90°﹣36°=54°,∴∠CEF=180°﹣2×54°=72°,
∵E为BC的中点,∴BE=CE,∴FE=CE,
∴∠ECF=(180°﹣72°)=54°,
∴∠DCF=90°﹣∠ECF=36°;
故答案为:36.
19、如图,在矩形ABCD中,AB=8,BC=6,点P为边AB上任意一点,过点P作PE⊥AC,PF⊥BD,垂足分别为E、F,则PE+PF= .
【分析】连接OP.由勾股定理得出AC=10,可求得OA=OB=5,由矩形的性质得出S矩形ABCD=AB?BC=48,S△AOB=S矩形ABCD=12,OA=OB=5,由S△AOB=S△AOP+S△BOP=OA?PE+OB?PF=OA(PE+PF)=×5×(PE+PF)=12求得答案.
【解析】连接OP,如图:
∵四边形ABCD是矩形,∴∠ABC=90°,OA=OC,OB=OD,AC=BD,
∴OA=OB,AC==10,
∴S矩形ABCD=AB?BC=48,S△AOB=S矩形ABCD=12,OA=OB=5,
∴S△AOB=S△AOP+S△BOP=OA?PE+OB?PF=OA(PE+PF)=×5×(PE+PF)=12,
∴PE+PF=; 故答案为:.
20、如图,在矩形ABCD中,AB=2,BC=,两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动,点C在第一象限,连接OC,则当OC为最大值时,点C的坐标是 .
【答案】(,)
【解析】解:E为AB的中点,当O,E及C共线时,OC最大,过C作CF⊥x轴于F,则∠CFO=90°,
此时,由勾股定理得:
OC=1+2=3,即
∵∠CBE=90°,∴∠ECB=30°,∠BEC=60°,∴∠AEO=60°,
∵在Rt△AOB中,E为斜边AB中点,∴AE=OE,∴△AOE等边三角形,∴∠AOE=60°,∴∠COB=90°-60°=30°,
由勾股定理得:
所以点C的坐标是
故答案为:
21、如图,在正方形ABCD中,E是AB边上的一点,BE=2,AE=3BE,P是AC上一动点,
则PB+PE的最小值是 .?
[解析] 如图,连接DE,交AC于点P,连接PB,则此时PB+PE的值最小.
∵四边形ABCD是正方形,∴点B,D关于AC对称,∴PB=PD,∴PB+PE=PD+PE=DE.
∵BE=2,AE=3BE,∴AE=6,AB=8,∴AD=8,∴DE=10,
故PB+PE的最小值是10.
22、如图,在正方形ABCD中,E为BC上一点,过点E作EF∥CD,交AD于F,交对角线BD于G,取DG的中点H,连结AH,EH,FH.下列结论:①∠EFH=45°;②△AHD≌△EHF;③∠AEF+∠HAD=45°; ④若=2,则.其中结论正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
【答案】A
【分析】①根据正方形的性质证明∠ADB=45°,进而得△DFG为等腰直角三角形,根据等腰三角形的三线合一性质得∠EFH=∠EFD=45°,故①正确;
②根据矩形性质得AF=EB,∠BEF=90°,再证明△AFH≌△EGH得EH=AH,进而证明△EHF≌△AHD,故②正确;
③由△EHF≌△AHD得∠EHF=∠AHD,怀AH=EH得∠AEF+∠HEF=45°,进而得∠AEF+∠HAD=45°,故③正确;
④如图,过点H作MN⊥AD于点M,与BC交于点N,设EC=FD=FG=x,则BE=AF=EG=2x,BC=DC=AB=AD=3x,HM=x,AM=x,HN=x,由勾股定理得AH2,再由三角形的面积公式得,便可判断④的正误,
【解答】证明:①在正方形ABCD中,∠ADC=∠C=90°,∠ADB=45°,
∵EF∥CD,∴∠EFD=90°,∴四边形EFDC是矩形.
在Rt△FDG中,∠FDG=45°,∴FD=FG,
∵H是DG中点,∴∠EFH=∠EFD=45°故①正确;
②∵四边形ABEF是矩形,∴AF=EB,∠BEF=90°,
∵BD平分∠ABC,∴∠EBG=∠EGB=45°,∴BE=GE,∴AF=EG.
在Rt△FGD中,H是DG的中点,∴FH=GH,FH⊥BD,
∵∠AFH=∠AFE+∠GFH=90°+45°=135°,
∠EGH=180°﹣∠EGB=180°﹣45°=135°,
∴∠AFH=∠EGH,∴△AFH≌△EGH(SAS),∴EH=AH,
∵EF=AD,FH=DH,∴△EHF≌△AHD(SSS),故②正确;
③∵△EHF≌△AHD,∴∠EHF=∠AHD,∴∠AHE=∠DHF=90°,
∵AH=EH,∴∠AEH=45°,即∠AEF+∠HEF=45°,
∵∠HEF=∠HAD,∴∠AEF+∠HAD=45°,故③正确;
④如图,过点H作MN⊥AD于点M,与BC交于点N,
设EC=FD=FG=x,则BE=AF=EG=2x,
∴BC=DC=AB=AD=3x,HM=x,AM=x,HN=x,
∴AH2=,∴=,故④错误;
故选:A.
三、解答题
23、如图,△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣4,1),C(﹣1,2).
(1)作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1;
(2)作出△ABC关于原点O成中心对称的△A2B2C2,写出B2和C2的坐标;
(3)直接写出△ABC绕原点O顺时针旋转一周扫过的图形面积.
【分析】(1)利用网格特点和旋转的性质画出A、B、C的对应点A1、B1、C1即可;
(2)利用关于原点对称的点的坐标特征写出A2、B2和C2的坐标,然后描点即可;
(3)△ABC绕原点O顺时针旋转一周扫过的图形为圆环,大圆半径为OB,小圆半径为OC,然后利用两圆的面积差求解.
【解答】解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作,B2(4,﹣1),C2(1,﹣2);
(3)OB==,OC==,
所以△ABC绕原点O顺时针旋转一周扫过的图形面积=π×()2﹣π×()2=12π.
24、如图,四边形ABCD中AC、BD相交于点O,延长AD至点E,连接EO并延长交CB的延长线于点F,∠E=∠F,AD=BC.
(1)求证:O是线段AC的中点:
(2)连接AF、EC,证明四边形AFCE是平行四边形.
【解析】证明:(1)∵∠E=∠F,∴AD∥BC,
∵AD=BC,∴四边形ABCD是平行四边形,∴AC,BD互相平分;即O是线段AC的中点.
(2)∵AD∥BC,∴∠EAC=∠FCA,
在△OAE和△OCF中, ,∴△OAE≌△OCF(ASA).
∴OE=OF,∴四边形AFCE是平行四边形.
25、已知:如图,在?ABCD中,对角线AC与BD相交于点E,G为AD的中点,连接CG并延长交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
解:(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠AFC=∠DCG.
又∵∠AGF=∠CGD,GA=GD,∴△AGF≌△DGC, ∴AF=CD,∴AB=AF.
(2)结论:四边形ACDF是矩形.
证明:∵AF=CD,AF∥CD,∴四边形ACDF是平行四边形.
∵四边形ABCD是平行四边形,∴∠BAD=∠BCD=120°,∴∠FAG=60°.
又∵AF=AB=AG,∴△AFG是等边三角形,∴AG=GF.
∵△AGF≌△DGC,∴FG=CG.
又∵AG=GD,∴AD=CF,∴四边形ACDF是矩形.
26、在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形.
【分析】(1)根据AAS证△AFE≌△DBE;
(2)利用(1)中全等三角形的对应边相等得到AF=BD.结合已知条件,利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形,由“直角三角形斜边的中线等于斜边的一半”得到AD=DC,从而得出结论.
【解答】证明:(1)∵AF∥BC,∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,∴AE=DE,BD=CD,
在△AFE和△DBE中,,∴△AFE≌△DBE(AAS);
(2)由(1)知,△AFE≌△DBE,则AF=DB.
∵DB=DC,∴AF=CD.
∵AF∥BC,∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,E是AD的中点,∴AD=DC=BC,
∴四边形ADCF是菱形.
27、如图,E为?ABCD中DC边的延长线上的一点,且CE=DC,连接AE交BC于点F,连接AC、BE.
(1)如图1,求证:AF=EF;
(2)连接BD交AC于点O,连接OF并延长交BE于点G,直接写出图中所有长度是OF二倍的线段.
【分析】(1)由AB∥CD可以得到∠BAF=∠E,∠ABF=∠ECF,再利用DC=CE即可证明△ABF≌△ECF,便可得结论;
(2)证明OF是△ACE的中位线,得CE=2OF,进而得AB=CD=CE=2OF,再证明四边形OGEC为平行四边形得OG=2OF.
【解答】解:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.
又∵DC=CE,∴AB=CE.
∵AB∥CD,∴∠BAF=∠E,∠ABF=∠ECF.∴△ABF≌△ECF(ASA),∴AF=EF;
(2)∵四边形ABCD为平行四边形,∴OB=OD,
∵AF=CF,∴OF是△ACE的中位线,∴OF∥CE,CE=2OF,
∵AB=CD=CE,∴AB=CD=CE=2OF,
∵AB∥CE,AB=CE,∴四边形ABEC为平行四边形,∴AC∥BE,
∵OF∥CE,∴四边形OGEC为平行四边形,∴OG=CE=2OF,
故图中长度是OF二倍的线段有AB,CD,CE,OG.
28、如图(a),在矩形纸片ABCD中,AB=3 cm,AD=5 cm,折叠纸片使点B落在边AD上的点E处,折痕为PQ,过点E作EF∥AB交PQ于点F,连接BF.
(1)求证:四边形BFEP为菱形.
(2)当点E在AD边上移动时,折痕的端点P,Q也随之移动.
①当点Q与点C重合时,如图(b),求菱形BFEP的边长;
②若限定点P,Q分别在边BA,BC上移动,求点E在边AD上移动的最大距离.
解:(1)证明:由折叠的性质,得PB=PE,BF=EF,∠BPF=∠EPF.
∵EF∥AB,∴∠BPF=∠EFP,∴∠EPF=∠EFP,
∴PE=EF,∴BF=EF=PE=PB,∴四边形BFEP为菱形.
(2)①∵四边形ABCD是矩形, ∴BC=AD=5 cm,CD=AB=3 cm,∠A=∠D=90°.
由折叠的性质,得CE=BC=5 cm.
在Rt△CDE中,DE==4 cm, ∴AE=AD-DE=5-4=1(cm).
在Rt△APE中,AE=1 cm,AP=3-PB=3-PE,∴PE2=12+(3-PE)2,解得PE=(cm),
∴菱形BFEP的边长为cm.
②当点Q与点C重合时,点E离点A最近,由①知,此时AE=1 cm;
当点P与点A重合时,如图所示:
点E离点A最远,此时四边形ABQE为正方形,AE=AB=3 cm.
∵3-1=2(cm), ∴点E在边AD上移动的最大距离为2 cm.
29、如图①所示,已知A、B为直线l上两点,点C为直线上方一动点,连接AC、BC,分别以AC、BC
为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1⊥l于点D1,过点E作EE1⊥l于点E1.
(1)如图②,当点E恰好在直线l上时(此时E1与E重合),试说明DD1=AB;
(2)在图①中,当D、E两点都在直线l的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并
说明理由;
(3)如图③,当点E在直线l的下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系.
图① 图② 图③
【解答】(1)证明:∵四边形CADF、CBEG是正方形,∴AD=CA,∠DAC=∠ABC=90°,
∴∠DAD1+∠CAB=90°,∵DD1⊥AB,∴∠DD1A=∠ABC=90°,∴∠DAD1+∠ADD1=90°,
∴∠ADD1=∠CAB,在△ADD1和△CAB中,,
∴△ADD1≌△CAB(AAS),∴DD1=AB;
(2)解:AB=DD1+EE1.证明:过点C作CH⊥AB于H,∵DD1⊥AB,∴∠DD1A=∠CHA=90°,
∴∠DAD1+∠ADD1=90°,∵四边形CADF是正方形,∴AD=CA,∠DAC=90°,
∴∠DAD1+∠CAH=90°,
∴∠ADD1=∠CAH,在△ADD1和△CAH中,,
∴△ADD1≌△CAH(AAS),∴DD1=AH;
同理:EE1=BH, ∴AB=AH+BH=DD1+EE1;
(3)解:AB=DD1-EE1.
证明:过点C作CH⊥AB于H,∵DD1⊥AB,∴∠DD1A=∠CHA=90°,
∴∠DAD1+∠ADD1=90°,∵四边形CADF是正方形,∴AD=CA,∠DAC=90°,
∴∠DAD1+∠CAH=90°, ∴∠ADD1=∠CAH,
在△ADD1和△CAH中,,∴△ADD1≌△CAH(AAS),∴DD1=AH;
同理:EE1=BH,∴AB=AH-BH=DD1-EE1.
30、如图,已知平行四边形中,对角线,交于点,是延长线上的点,且 是等边三角形.
(1)求证:四边形是菱形;
(2)若,求证:四边形是正方形.
【答案】(1)见解析;(2)见解析
【分析】(1)根据对角线互相垂直的平行四边形是菱形.由题意易得△AOE≌△COE,∴∠AOE=∠COE=90°,∴BE⊥AC,∴四边形ABCD是菱形;
(2)根据有一个角是90°的菱形是正方形.由题意易得∠ADO=∠DAE+∠DEA=15°+30°=45°,∵四边形ABCD是菱形,∴∠ADC=2∠ADO=90°,∴四边形ABCD是正方形.
【解析】解:证明:(1)∵四边形ABCD是平行四边形,∴AO=CO.
又∵△ACE是等边三角形,∴EO⊥AC(三线合一),即AC⊥BD,
∴四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形).
(2)∵四边形ABCD是平行四边形,∴AO=CO.
又∵△ACE是等边三角形,∴EO平分∠AEC(三线合一),∴∠AED=∠AEC=×60°=30°,
又∵∠AED=2∠EAD∴∠EAD=15°,
∴∠ADO=∠DAE+∠DEA=15°+30°=45°(三角形的一一个外角等于和它外角不相邻的两内角之和),
∵四边形ABCD是菱形,∴∠ADC=2∠ADO=90°,∴平行四边形ABCD是正方形.
-苏科版八年级数学下册
一、选择题
1、下列图案中,是中心对称图形的是( )
A. B. C. D.
2、如图,在Rt△ABC中,∠C=90°,把△ABC绕AC边的中点M旋转后得△DEF,若直角顶点F恰好落在AB边上,且DE边交AB边于点G,若AC=4,BC=3,则AG的长为( )
A. B. C. D.1
3、在下列性质中,平行四边形不一定具有的性质是( )
A.邻角互补 B.对角相等
C.内角和为360° D.对角互补
4、下列四个选项中,能判断四边形ABCD是平行四边形的是( )
A.AB=CD,AC=BD B.∠A=∠B,∠B=∠C
C.AB=CD,AD∥BC D.AB∥CD,∠A=∠C
5、菱形的对角线不具备的性质是( )
A.对角线互相平分 B.对角线一定相等
C.对角线一定垂直 D.对角线平分一组对角
6、如图所示,在矩形ABCD中,E为AD上一点,EF⊥CE交AB于点F,若DE=2,矩形ABCD的周长为16,且CE=EF,求AE的长( )
A.2 B.3 C.4 D.6
7、如图,在矩形ABCD中,AB=4,BC=6,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,连接CE,△DEC的周长为( )
A.10 B.11 C.12 D.13
8、如图,已知点E、F分别是四边形ABCD的边AD、BC的中点,G、H分别是对角线BD、AC的中点,要使四边形EGFH是菱形,则四边形ABCD需满足的条件是( )
A.AB=CD B.AC=BD C.AC⊥BD D.AD=BC
9、如图,在平面直角坐标系中,?ABCD的顶点坐标分别为A(3,a),B(2,2),C(b,3),D(8,6),则a+b的值为( )
A.8 B.9 C.12 D.11
10、如图,?ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB?AC;③OB=AB;④OE=BC,成立的个数有( )
A.1个 B.2个 C.3个 D.4个
11、如图,在边长为4的正方形ABCD中,点E、F分别是边BC、CD上的动点,且BE=CF,连接BF、DE,则BF+DE的最小值为( )
A. B. C. D.
12、如图,正方形ABCD的边长为2,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A.2 B.2 C. D.
二、填空题
13、如图,△ABC与△A1B1C1关于点O成中心对称.有下列说法:①∠BAC=∠B1A1C1;②AC=A1C1;③OA=OA1;
④△ABC与△A1B1C1的面积相等.其中正确的有 (只填序号).?
14、如图,在△ABC中,AB=5,AC=6,BC=7,D,E,F分别是边AB,AC,BC的中点,连接DE,DF,EF,
则△DEF的周长是 .?
15、如图,点O是?ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB,G、H是BC边上的点,且GH=BC,若,则= .
16、如图,在矩形ABCD中,BC=20 cm,点P和点Q分别从点B和点D同时出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3 cm/s和2 cm/s,则最快 s后,四边形ABPQ成为矩形.?
17、如图,矩形ABCD的对角线交于点O,点E在线段AO上,且DE=DC,若∠EDO=15°,
则∠DEC=______°.
18、如图,矩形ABCD中,E为BC的中点,将△ABE沿直线AE折叠,使点B落在点F处,连接FC,若∠DAF=18°,则∠DCF= 度.
19、如图,在矩形ABCD中,AB=8,BC=6,点P为边AB上任意一点,过点P作PE⊥AC,PF⊥BD,垂足分别为E、F,则PE+PF= .
20、如图,在矩形ABCD中,AB=2,BC=,两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动,点C在第一象限,连接OC,则当OC为最大值时,点C的坐标是 .
21、如图,在正方形ABCD中,E是AB边上的一点,BE=2,AE=3BE,P是AC上一动点,
则PB+PE的最小值是 .?
22、如图,在正方形ABCD中,E为BC上一点,过点E作EF∥CD,交AD于F,交对角线BD于G,取DG的中点H,连结AH,EH,FH.下列结论:①∠EFH=45°;②△AHD≌△EHF;③∠AEF+∠HAD=45°; ④若=2,则.其中结论正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
三、解答题
23、如图,△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣4,1),C(﹣1,2).
(1)作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1;
(2)作出△ABC关于原点O成中心对称的△A2B2C2,写出B2和C2的坐标;
(3)直接写出△ABC绕原点O顺时针旋转一周扫过的图形面积.
24、如图,四边形ABCD中AC、BD相交于点O,延长AD至点E,连接EO并延长交CB的延长线于点F,∠E=∠F,AD=BC.
(1)求证:O是线段AC的中点:
(2)连接AF、EC,证明四边形AFCE是平行四边形.
25、已知:如图,在?ABCD中,对角线AC与BD相交于点E,G为AD的中点,连接CG并延长交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
26、在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形.
27、如图,E为?ABCD中DC边的延长线上的一点,且CE=DC,连接AE交BC于点F,连接AC、BE.
(1)如图1,求证:AF=EF;
(2)连接BD交AC于点O,连接OF并延长交BE于点G,直接写出图中所有长度是OF二倍的线段.
28、如图(a),在矩形纸片ABCD中,AB=3 cm,AD=5 cm,折叠纸片使点B落在边AD上的点E处,折痕为PQ,过点E作EF∥AB交PQ于点F,连接BF.
(1)求证:四边形BFEP为菱形.
(2)当点E在AD边上移动时,折痕的端点P,Q也随之移动.
①当点Q与点C重合时,如图(b),求菱形BFEP的边长;
②若限定点P,Q分别在边BA,BC上移动,求点E在边AD上移动的最大距离.
29、如图①所示,已知A、B为直线l上两点,点C为直线上方一动点,连接AC、BC,分别以AC、BC
为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1⊥l于点D1,过点E作EE1⊥l于点E1.
(1)如图②,当点E恰好在直线l上时(此时E1与E重合),试说明DD1=AB;
(2)在图①中,当D、E两点都在直线l的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并
说明理由;
(3)如图③,当点E在直线l的下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系.
图① 图② 图③
30、如图,已知平行四边形中,对角线,交于点,是延长线上的点,且 是等边三角形.
(1)求证:四边形是菱形;
(2)若,求证:四边形是正方形.
五一假期专题复习提升训练卷1(9章中心对称图形-平行四边形)
-苏科版八年级数学下册(解析)
一、选择题
1、下列图案中,是中心对称图形的是( )
A. B. C. D.
解:A、是中心对称图形,故本选项符合题意;
B、不是中心对称图形,故本选项不合题意;
C、不是中心对称图形,故本选项不合题意;
D、不是中心对称图形,故本选项不合题意.
故选:A.
2、如图,在Rt△ABC中,∠C=90°,把△ABC绕AC边的中点M旋转后得△DEF,若直角顶点F恰好落在AB边上,且DE边交AB边于点G,若AC=4,BC=3,则AG的长为( )
A. B. C. D.1
解:∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB=5,
∵点M是AC边的中点,∴CM=AM=AC=2,
∵把△ABC绕AC边的中点M旋转后得△DEF,若直角顶点F恰好落在AB边上,
∴CM=FM=2,∠D=∠A,∠C=∠DFE,AB=DE,∴AM=MF,∴∠A=∠AFM,
∴∠D=∠AFD,∴DG=FG,
∵∠D+∠E=∠DFG+∠GFE=90°,
∴∠E=∠EFG,∴EG=FG,∴FG=DE=,
∵AM=CM=FM=AC,∴∠AFC=90°,∴CF==,
∴AF==,∴AG=AF﹣FG=﹣=,
故选:A.
3、在下列性质中,平行四边形不一定具有的性质是( )
A.邻角互补 B.对角相等
C.内角和为360° D.对角互补
解:平行四边形邻角互补,对角相等,内角和为360°,不具备的性质是对角互补,
故选:D.
4、下列四个选项中,能判断四边形ABCD是平行四边形的是( )
A.AB=CD,AC=BD B.∠A=∠B,∠B=∠C
C.AB=CD,AD∥BC D.AB∥CD,∠A=∠C
解:A、AB=CD,AC=BD不能判定四边形ABCD是平行四边形,故此选项错误;
B、∠A=∠B,∠B=∠C不能判定四边形ABCD是平行四边形,故此选项错误;
C、AB=CD,AD∥BC不能判定四边形ABCD是平行四边形,故此选项错误;
D、∵AB∥CD,∴∠A+∠D=∠B+∠C=180°,
∵∠A=∠C,∴∠B=∠D,∴四边形ABCD是平行四边形,故此选项正确;
故选:D.
5、菱形的对角线不具备的性质是( )
A.对角线互相平分 B.对角线一定相等
C.对角线一定垂直 D.对角线平分一组对角
解:菱形的性质:四条边都相等,对角线互相垂直平分,是轴对称图形,并且每一条对角线平分一组对角;
菱形的对角线不一定相等;
故选:B.
6、如图所示,在矩形ABCD中,E为AD上一点,EF⊥CE交AB于点F,若DE=2,矩形ABCD的周长为16,且CE=EF,求AE的长( )
A.2 B.3 C.4 D.6
解:∵四边形ABCD为矩形,∴∠A=∠D=90°,
∵EF⊥CE,∴∠CEF=90°,∴∠CED+∠AEF=90°,
∵∠CED+∠DCE=90°,∴∠DCE=∠AEF,
在△AEF和△DCE中,,∴△AEF≌△DCE(AAS),∴AE=DC,
由题意可知:2(AE+DE+CD)=16,DE=2,∴2AE=6,∴AE=3;
故选:B.
7、如图,在矩形ABCD中,AB=4,BC=6,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,连接CE,△DEC的周长为( )
A.10 B.11 C.12 D.13
解:设DE=x,则AE=6﹣x,
∵四边形ABCD是矩形,∴∠ADC=90°,DC=AB=4,AD=BC=6,AO=OC,
∵EF⊥AC,AO=OC,∴AE=CE=6﹣x,
在Rt△DEC中,由勾股定理得:DE2+DC2=EC2,
即x2+42=(6﹣x)2,解得:x=,
即DE=,CE=AE=6﹣=,
∴△DEC的周长为DE+CE+DC=++4=10,
故选:A.
8、如图,已知点E、F分别是四边形ABCD的边AD、BC的中点,G、H分别是对角线BD、AC的中点,要使四边形EGFH是菱形,则四边形ABCD需满足的条件是( )
A.AB=CD B.AC=BD C.AC⊥BD D.AD=BC
解:∵点E、F分别是四边形ABCD的边AD、BC的中点,G、H分别是对角线BD、AC的中点,
∴EG=FH=AB,EH=FG=CD,
∵当EG=FH=GF=EH时,四边形EGFH是菱形,
∴当AB=CD时,四边形EGFH是菱形.
故选:A.
9、如图,在平面直角坐标系中,?ABCD的顶点坐标分别为A(3,a),B(2,2),C(b,3),D(8,6),则a+b的值为( )
A.8 B.9 C.12 D.11
解:如图,连接AC、BD交于点O′.
∵四边形ABCD是平行四边形,∴AO′=O′C,BO′=O′D,
∵A(3,a),B(2,2),C(b,3),D(8,6),
∴=,=,
∴a=5,b=7,∴a+b=12,
故选:C.
10、如图,?ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB?AC;③OB=AB;④OE=BC,成立的个数有( )
A.1个 B.2个 C.3个 D.4个
【考点】平行四边形的性质;等腰三角形的判定与性质;等边三角形的判定与性质;含30度角的直角三角形.
【分析】由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据AE平分∠BAD,得到∠BAE=∠EAD=60°推出△ABE是等边三角形,由于AB=BC,得到AE=BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;由于AC⊥AB,得到S?ABCD=AB?AC,故②正确,根据AB=BC,OB=BD,且BD>BC,得到AB≠OB,故③错误;根据三角形的中位线定理得到OE=AB,于是得到OE=BC,故④正确.
【解答】解:∵四边形ABCD是平行四边形,∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,∴∠BAE=∠EAD=60°∴△ABE是等边三角形,∴AE=AB=BE,
∵AB=BC,∴AE=BC,∴∠BAC=90°,∴∠CAD=30°,故①正确;
∵AC⊥AB,∴S?ABCD=AB?AC,故②正确,
∵AB=BC,OB=BD,∵BD>BC,∴AB≠OB,故③错误;
∵CE=BE,CO=OA,∴OE=AB,∴OE=BC,故④正确.
故选:C.
11、如图,在边长为4的正方形ABCD中,点E、F分别是边BC、CD上的动点,且BE=CF,连接BF、DE,则BF+DE的最小值为( )
A. B. C. D.
解:连接AE,如图1,∵四边形ABCD是正方形,∴AB=BC,∠ABE=∠BCF=90°.
又BE=CF,∴△ABE≌△BCF(SAS).∴AE=BF. 所以BF+DE最小值等于AE+DE最小值.
作点A关于BC的对称点H点,如图2,连接BH,则A、B、H三点共线,
连接DH,DH与BC的交点即为所求的E点.根据对称性可知AE=HE, 所以AE+DE=DH.
在Rt△ADH中,DH=,
∴BF+DE最小值为.
故选:D.
12、如图,正方形ABCD的边长为2,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A.2 B.2 C. D.
【考点】轴对称﹣最短路线问题;正方形的性质.
【分析】由于点B与D关于AC对称,所以连接BE,与AC的交点即为P点.此时PD+PE=BE最小,而BE是等边△ABE的边,BE=AB,由正方形ABCD的面积为4,可求出AB的长,从而得出结果.
【解答】解:连接BD,与AC交于点F.
∵点B与D关于AC对称,∴PD=PB,∴PD+PE=PB+PE=BE最小.
∵正方形ABCD的边长为2,∴AB=2.
又∵△ABE是等边三角形,∴BE=AB=2.∴所求最小值为2.
故选:A.
二、填空题
13、如图,△ABC与△A1B1C1关于点O成中心对称.有下列说法:①∠BAC=∠B1A1C1;②AC=A1C1;③OA=OA1;
④△ABC与△A1B1C1的面积相等.其中正确的有 (只填序号).?
[答案] ①②③④
[解析] 中心对称的两个图形全等,所以∠BAC=∠B1A1C1,AC=A1C1,△ABC与△A1B1C1的面积相等,故①②④正确;对称点到对称中心的距离相等,故③正确.故答案为①②③④.
14、如图,在△ABC中,AB=5,AC=6,BC=7,D,E,F分别是边AB,AC,BC的中点,连接DE,DF,EF,
则△DEF的周长是 .?
[答案] 9
[解析] ∵D,E,F分别是边AB,AC,BC的中点,∴DE=BC=3.5,DF=AC=3,EF=AB=2.5,
∴△DEF的周长=DE+DF+EF=9.
故答案为9.
15、如图,点O是?ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB,G、H是BC边上的点,且GH=BC,若,则= .
【答案】2
【解析】解:连接AC、BD,如图,
∵点O是?ABCD的对称中心,∴AC、BD交于点O,∴S△AOB=S△BOC,
∵EF=AB,∴S△EOF=S△AOB,
∵GH=BC,∴S△OGH=S△BOC,
∴S△EOF:S△OGH=3:2,
∵,∴=2.
故答案为:2.
16、如图,在矩形ABCD中,BC=20 cm,点P和点Q分别从点B和点D同时出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3 cm/s和2 cm/s,则最快 s后,四边形ABPQ成为矩形.?
[答案] 4
[解析] 设最快x s后,四边形ABPQ成为矩形,由BP=AQ,得3x=20-2x.
解得x=4.
故答案为4.
17、如图,矩形ABCD的对角线交于点O,点E在线段AO上,且DE=DC,若∠EDO=15°,
则∠DEC=______°.
【答案】55
【解析】解:设∠DEC=x,
∵DE=DC,∴∠DCE=x,
∵四边形ABCD为矩形,∴∠ODC=∠DCE=x,
∴∠DOE=∠OCD+∠ODC=2x,
∵△DOE内角和为180°,∴,解得:,即∠DEC=,
故答案为:55.
18、如图,矩形ABCD中,E为BC的中点,将△ABE沿直线AE折叠,使点B落在点F处,连接FC,若∠DAF=18°,则∠DCF= 度.
【分析】由折叠的性质得:FE=BE,∠FAE=∠BAE,∠AEB=∠AEF,求出∠BAE=∠FAE=36°,由直角三角形的性质得出∠AEF=∠AEB=54°,求出∠CEF=72°,求出FE=CE,由等腰三角形的性质求出∠ECF=54°,即可得出∠DCF的度数.
【解析】∵四边形ABCD是矩形,∴∠BAD=∠B=∠BCD=90°,
由折叠的性质得:FE=BE,∠FAE=∠BAE,∠AEB=∠AEF,
∵∠DAF=18°,∴∠BAE=∠FAE=(90°﹣18°)=36°,
∴∠AEF=∠AEB=90°﹣36°=54°,∴∠CEF=180°﹣2×54°=72°,
∵E为BC的中点,∴BE=CE,∴FE=CE,
∴∠ECF=(180°﹣72°)=54°,
∴∠DCF=90°﹣∠ECF=36°;
故答案为:36.
19、如图,在矩形ABCD中,AB=8,BC=6,点P为边AB上任意一点,过点P作PE⊥AC,PF⊥BD,垂足分别为E、F,则PE+PF= .
【分析】连接OP.由勾股定理得出AC=10,可求得OA=OB=5,由矩形的性质得出S矩形ABCD=AB?BC=48,S△AOB=S矩形ABCD=12,OA=OB=5,由S△AOB=S△AOP+S△BOP=OA?PE+OB?PF=OA(PE+PF)=×5×(PE+PF)=12求得答案.
【解析】连接OP,如图:
∵四边形ABCD是矩形,∴∠ABC=90°,OA=OC,OB=OD,AC=BD,
∴OA=OB,AC==10,
∴S矩形ABCD=AB?BC=48,S△AOB=S矩形ABCD=12,OA=OB=5,
∴S△AOB=S△AOP+S△BOP=OA?PE+OB?PF=OA(PE+PF)=×5×(PE+PF)=12,
∴PE+PF=; 故答案为:.
20、如图,在矩形ABCD中,AB=2,BC=,两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动,点C在第一象限,连接OC,则当OC为最大值时,点C的坐标是 .
【答案】(,)
【解析】解:E为AB的中点,当O,E及C共线时,OC最大,过C作CF⊥x轴于F,则∠CFO=90°,
此时,由勾股定理得:
OC=1+2=3,即
∵∠CBE=90°,∴∠ECB=30°,∠BEC=60°,∴∠AEO=60°,
∵在Rt△AOB中,E为斜边AB中点,∴AE=OE,∴△AOE等边三角形,∴∠AOE=60°,∴∠COB=90°-60°=30°,
由勾股定理得:
所以点C的坐标是
故答案为:
21、如图,在正方形ABCD中,E是AB边上的一点,BE=2,AE=3BE,P是AC上一动点,
则PB+PE的最小值是 .?
[解析] 如图,连接DE,交AC于点P,连接PB,则此时PB+PE的值最小.
∵四边形ABCD是正方形,∴点B,D关于AC对称,∴PB=PD,∴PB+PE=PD+PE=DE.
∵BE=2,AE=3BE,∴AE=6,AB=8,∴AD=8,∴DE=10,
故PB+PE的最小值是10.
22、如图,在正方形ABCD中,E为BC上一点,过点E作EF∥CD,交AD于F,交对角线BD于G,取DG的中点H,连结AH,EH,FH.下列结论:①∠EFH=45°;②△AHD≌△EHF;③∠AEF+∠HAD=45°; ④若=2,则.其中结论正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
【答案】A
【分析】①根据正方形的性质证明∠ADB=45°,进而得△DFG为等腰直角三角形,根据等腰三角形的三线合一性质得∠EFH=∠EFD=45°,故①正确;
②根据矩形性质得AF=EB,∠BEF=90°,再证明△AFH≌△EGH得EH=AH,进而证明△EHF≌△AHD,故②正确;
③由△EHF≌△AHD得∠EHF=∠AHD,怀AH=EH得∠AEF+∠HEF=45°,进而得∠AEF+∠HAD=45°,故③正确;
④如图,过点H作MN⊥AD于点M,与BC交于点N,设EC=FD=FG=x,则BE=AF=EG=2x,BC=DC=AB=AD=3x,HM=x,AM=x,HN=x,由勾股定理得AH2,再由三角形的面积公式得,便可判断④的正误,
【解答】证明:①在正方形ABCD中,∠ADC=∠C=90°,∠ADB=45°,
∵EF∥CD,∴∠EFD=90°,∴四边形EFDC是矩形.
在Rt△FDG中,∠FDG=45°,∴FD=FG,
∵H是DG中点,∴∠EFH=∠EFD=45°故①正确;
②∵四边形ABEF是矩形,∴AF=EB,∠BEF=90°,
∵BD平分∠ABC,∴∠EBG=∠EGB=45°,∴BE=GE,∴AF=EG.
在Rt△FGD中,H是DG的中点,∴FH=GH,FH⊥BD,
∵∠AFH=∠AFE+∠GFH=90°+45°=135°,
∠EGH=180°﹣∠EGB=180°﹣45°=135°,
∴∠AFH=∠EGH,∴△AFH≌△EGH(SAS),∴EH=AH,
∵EF=AD,FH=DH,∴△EHF≌△AHD(SSS),故②正确;
③∵△EHF≌△AHD,∴∠EHF=∠AHD,∴∠AHE=∠DHF=90°,
∵AH=EH,∴∠AEH=45°,即∠AEF+∠HEF=45°,
∵∠HEF=∠HAD,∴∠AEF+∠HAD=45°,故③正确;
④如图,过点H作MN⊥AD于点M,与BC交于点N,
设EC=FD=FG=x,则BE=AF=EG=2x,
∴BC=DC=AB=AD=3x,HM=x,AM=x,HN=x,
∴AH2=,∴=,故④错误;
故选:A.
三、解答题
23、如图,△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣4,1),C(﹣1,2).
(1)作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1;
(2)作出△ABC关于原点O成中心对称的△A2B2C2,写出B2和C2的坐标;
(3)直接写出△ABC绕原点O顺时针旋转一周扫过的图形面积.
【分析】(1)利用网格特点和旋转的性质画出A、B、C的对应点A1、B1、C1即可;
(2)利用关于原点对称的点的坐标特征写出A2、B2和C2的坐标,然后描点即可;
(3)△ABC绕原点O顺时针旋转一周扫过的图形为圆环,大圆半径为OB,小圆半径为OC,然后利用两圆的面积差求解.
【解答】解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作,B2(4,﹣1),C2(1,﹣2);
(3)OB==,OC==,
所以△ABC绕原点O顺时针旋转一周扫过的图形面积=π×()2﹣π×()2=12π.
24、如图,四边形ABCD中AC、BD相交于点O,延长AD至点E,连接EO并延长交CB的延长线于点F,∠E=∠F,AD=BC.
(1)求证:O是线段AC的中点:
(2)连接AF、EC,证明四边形AFCE是平行四边形.
【解析】证明:(1)∵∠E=∠F,∴AD∥BC,
∵AD=BC,∴四边形ABCD是平行四边形,∴AC,BD互相平分;即O是线段AC的中点.
(2)∵AD∥BC,∴∠EAC=∠FCA,
在△OAE和△OCF中, ,∴△OAE≌△OCF(ASA).
∴OE=OF,∴四边形AFCE是平行四边形.
25、已知:如图,在?ABCD中,对角线AC与BD相交于点E,G为AD的中点,连接CG并延长交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
解:(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠AFC=∠DCG.
又∵∠AGF=∠CGD,GA=GD,∴△AGF≌△DGC, ∴AF=CD,∴AB=AF.
(2)结论:四边形ACDF是矩形.
证明:∵AF=CD,AF∥CD,∴四边形ACDF是平行四边形.
∵四边形ABCD是平行四边形,∴∠BAD=∠BCD=120°,∴∠FAG=60°.
又∵AF=AB=AG,∴△AFG是等边三角形,∴AG=GF.
∵△AGF≌△DGC,∴FG=CG.
又∵AG=GD,∴AD=CF,∴四边形ACDF是矩形.
26、在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形.
【分析】(1)根据AAS证△AFE≌△DBE;
(2)利用(1)中全等三角形的对应边相等得到AF=BD.结合已知条件,利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形,由“直角三角形斜边的中线等于斜边的一半”得到AD=DC,从而得出结论.
【解答】证明:(1)∵AF∥BC,∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,∴AE=DE,BD=CD,
在△AFE和△DBE中,,∴△AFE≌△DBE(AAS);
(2)由(1)知,△AFE≌△DBE,则AF=DB.
∵DB=DC,∴AF=CD.
∵AF∥BC,∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,E是AD的中点,∴AD=DC=BC,
∴四边形ADCF是菱形.
27、如图,E为?ABCD中DC边的延长线上的一点,且CE=DC,连接AE交BC于点F,连接AC、BE.
(1)如图1,求证:AF=EF;
(2)连接BD交AC于点O,连接OF并延长交BE于点G,直接写出图中所有长度是OF二倍的线段.
【分析】(1)由AB∥CD可以得到∠BAF=∠E,∠ABF=∠ECF,再利用DC=CE即可证明△ABF≌△ECF,便可得结论;
(2)证明OF是△ACE的中位线,得CE=2OF,进而得AB=CD=CE=2OF,再证明四边形OGEC为平行四边形得OG=2OF.
【解答】解:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.
又∵DC=CE,∴AB=CE.
∵AB∥CD,∴∠BAF=∠E,∠ABF=∠ECF.∴△ABF≌△ECF(ASA),∴AF=EF;
(2)∵四边形ABCD为平行四边形,∴OB=OD,
∵AF=CF,∴OF是△ACE的中位线,∴OF∥CE,CE=2OF,
∵AB=CD=CE,∴AB=CD=CE=2OF,
∵AB∥CE,AB=CE,∴四边形ABEC为平行四边形,∴AC∥BE,
∵OF∥CE,∴四边形OGEC为平行四边形,∴OG=CE=2OF,
故图中长度是OF二倍的线段有AB,CD,CE,OG.
28、如图(a),在矩形纸片ABCD中,AB=3 cm,AD=5 cm,折叠纸片使点B落在边AD上的点E处,折痕为PQ,过点E作EF∥AB交PQ于点F,连接BF.
(1)求证:四边形BFEP为菱形.
(2)当点E在AD边上移动时,折痕的端点P,Q也随之移动.
①当点Q与点C重合时,如图(b),求菱形BFEP的边长;
②若限定点P,Q分别在边BA,BC上移动,求点E在边AD上移动的最大距离.
解:(1)证明:由折叠的性质,得PB=PE,BF=EF,∠BPF=∠EPF.
∵EF∥AB,∴∠BPF=∠EFP,∴∠EPF=∠EFP,
∴PE=EF,∴BF=EF=PE=PB,∴四边形BFEP为菱形.
(2)①∵四边形ABCD是矩形, ∴BC=AD=5 cm,CD=AB=3 cm,∠A=∠D=90°.
由折叠的性质,得CE=BC=5 cm.
在Rt△CDE中,DE==4 cm, ∴AE=AD-DE=5-4=1(cm).
在Rt△APE中,AE=1 cm,AP=3-PB=3-PE,∴PE2=12+(3-PE)2,解得PE=(cm),
∴菱形BFEP的边长为cm.
②当点Q与点C重合时,点E离点A最近,由①知,此时AE=1 cm;
当点P与点A重合时,如图所示:
点E离点A最远,此时四边形ABQE为正方形,AE=AB=3 cm.
∵3-1=2(cm), ∴点E在边AD上移动的最大距离为2 cm.
29、如图①所示,已知A、B为直线l上两点,点C为直线上方一动点,连接AC、BC,分别以AC、BC
为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1⊥l于点D1,过点E作EE1⊥l于点E1.
(1)如图②,当点E恰好在直线l上时(此时E1与E重合),试说明DD1=AB;
(2)在图①中,当D、E两点都在直线l的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并
说明理由;
(3)如图③,当点E在直线l的下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系.
图① 图② 图③
【解答】(1)证明:∵四边形CADF、CBEG是正方形,∴AD=CA,∠DAC=∠ABC=90°,
∴∠DAD1+∠CAB=90°,∵DD1⊥AB,∴∠DD1A=∠ABC=90°,∴∠DAD1+∠ADD1=90°,
∴∠ADD1=∠CAB,在△ADD1和△CAB中,,
∴△ADD1≌△CAB(AAS),∴DD1=AB;
(2)解:AB=DD1+EE1.证明:过点C作CH⊥AB于H,∵DD1⊥AB,∴∠DD1A=∠CHA=90°,
∴∠DAD1+∠ADD1=90°,∵四边形CADF是正方形,∴AD=CA,∠DAC=90°,
∴∠DAD1+∠CAH=90°,
∴∠ADD1=∠CAH,在△ADD1和△CAH中,,
∴△ADD1≌△CAH(AAS),∴DD1=AH;
同理:EE1=BH, ∴AB=AH+BH=DD1+EE1;
(3)解:AB=DD1-EE1.
证明:过点C作CH⊥AB于H,∵DD1⊥AB,∴∠DD1A=∠CHA=90°,
∴∠DAD1+∠ADD1=90°,∵四边形CADF是正方形,∴AD=CA,∠DAC=90°,
∴∠DAD1+∠CAH=90°, ∴∠ADD1=∠CAH,
在△ADD1和△CAH中,,∴△ADD1≌△CAH(AAS),∴DD1=AH;
同理:EE1=BH,∴AB=AH-BH=DD1-EE1.
30、如图,已知平行四边形中,对角线,交于点,是延长线上的点,且 是等边三角形.
(1)求证:四边形是菱形;
(2)若,求证:四边形是正方形.
【答案】(1)见解析;(2)见解析
【分析】(1)根据对角线互相垂直的平行四边形是菱形.由题意易得△AOE≌△COE,∴∠AOE=∠COE=90°,∴BE⊥AC,∴四边形ABCD是菱形;
(2)根据有一个角是90°的菱形是正方形.由题意易得∠ADO=∠DAE+∠DEA=15°+30°=45°,∵四边形ABCD是菱形,∴∠ADC=2∠ADO=90°,∴四边形ABCD是正方形.
【解析】解:证明:(1)∵四边形ABCD是平行四边形,∴AO=CO.
又∵△ACE是等边三角形,∴EO⊥AC(三线合一),即AC⊥BD,
∴四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形).
(2)∵四边形ABCD是平行四边形,∴AO=CO.
又∵△ACE是等边三角形,∴EO平分∠AEC(三线合一),∴∠AED=∠AEC=×60°=30°,
又∵∠AED=2∠EAD∴∠EAD=15°,
∴∠ADO=∠DAE+∠DEA=15°+30°=45°(三角形的一一个外角等于和它外角不相邻的两内角之和),
∵四边形ABCD是菱形,∴∠ADC=2∠ADO=90°,∴平行四边形ABCD是正方形.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
