北师大版七上数学 第一章丰富的图形世界 课件(共133张ppt)
文档属性
| 名称 | 北师大版七上数学 第一章丰富的图形世界 课件(共133张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 11.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-30 19:04:40 | ||
图片预览











文档简介
(共133张PPT)
1.生活中的立体图形(一)
1.生活中的立体图形(二)
2.展开与折叠(一)
2.展开与折叠(二)
3.截一个几何体
4.从三个方向看物体的形状
回顾与思考
第一章
丰富的图形世界
情境导入
下列图片中有哪些你熟悉的几何体?
情境导入
下列图片中有哪些你熟悉的几何体?
情境导入
下列图片中有哪些你熟悉的几何体?
情境导入
下列图片中有哪些你熟悉的几何体?
情境导入
下列图片中有哪些你熟悉的几何体?
情境导入
下列图片中有哪些你熟悉的几何体?
情境导入
下列图片中有哪些你熟悉的几何体?
1.生活中的立体图形(一)
1.生活中的立体图形(一)
汝州外国语
卢天亮
第一章
丰富的图形世界
找找看
下图中,哪些物体的形状与你在小学学过的几何体类似?
结论
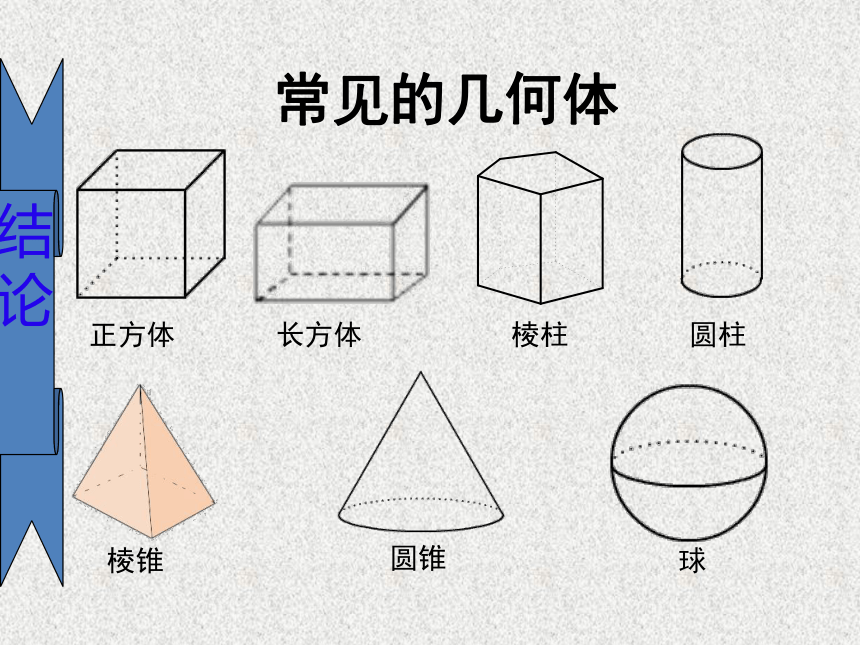
常见的几何体
圆柱
圆锥
正方体
长方体
棱柱
球
棱锥
探索新知
多面体是指各个面都是平面的几何体.
巩固练习
说一说生活中哪些物体的形状分别类似于棱柱、圆柱、圆锥与球.
探索新知
常见几何体都有何特征?
圆柱:底面是圆形,侧面是曲面,只有一个侧面,有两个底面,底面互相平行且相等.
棱柱:底面是多边形,侧面是正方形或长方形,n棱柱有n个侧面,有两个底面,底面互相平行且相等.
圆锥:底面是圆形,侧面是曲面,只有一个侧面和一个底面.
棱锥:底面是多边形,侧面是三角形,有多个侧面.
球:只有一个曲面.
你行吗
请按适当的标准对下列几何体进行分类.
(1)
(2)
(3)
(4)
(5)
(6)
按“柱、锥、球”划分:
(3)(4)(5)是一类,组成它们的面中至少有一个是曲的;(1)(2)(6)一类,组成它们的各面都是平的.
(1)(2)(4)(6)是柱体.(5)是锥体.(3)是球体.
按面的曲或平划分:
探索新知
常见几何体的分类
巩固练习
探索新知
棱柱的侧棱、底面、侧面分别有什么特点?
棱柱的所有侧棱长都相等.
棱柱的上下底面的形状相同.
棱柱的侧面是平行四边形.
认识棱柱
上、下底面是相同的多边形,侧面都是平行四边形的几何图形叫做棱柱
探索新知
棱柱、棱锥是按底面图形的边数来命名的.
考考你
长方形、正方形都是四棱柱.
长方体、正方体是棱柱吗?
探索新知
探索棱柱的特性
棱
柱
顶
点
棱
数
面
数
三棱柱
四棱柱
五棱柱
六棱柱
6
9
5
8
12
6
10
15
7
12
18
8
你能马上说出十棱柱的顶点数、棱数、面数吗?
你能马上说出n棱柱的顶点数、棱数、面数吗?
结论
n棱柱有(n+2)个面,3n条棱,2n个顶点.
探索新知
棱柱有直棱柱和斜棱柱.
本书只讨论直棱柱,简称棱柱
巩固练习
1、一个六棱柱模型如图所示,它的底面边长都是5cm,侧棱长为4cm.观察这个模型,回答下列问题:
(1)这个六棱柱的几个面分别是什么形状?那些面的形状、大小完全相同?
(2)这个六棱柱的所有侧面
的面积之和是多少?
巩固练习
2、圆柱和棱柱有很多相同点,下面的这个几何体与圆柱和棱柱又有什么相同点?
归纳小结
谈谈你的收获.
作业布置
作业
课本第4页,习题1.1,知识技能,1;数学理解,3.
THANK
YOU
!
See
you
next
class!
复习导入
1.
生活中常见的几何体有哪些?你能将它们按一定的标准分类吗?
2.棱柱有些什么性质?
第一章
丰富的图形世界
探索新知
从以上问题中,你能得到什么结论吗?
1.面有平面、曲面之分;线有直线、曲线之分.
2.面与面相交得到线,线与线相交得到点.
探索新知
组成几何图形的基本元素是:点、线、面.
探索新知
观察动画,你发现了什么?
点动成线、线动成面、面动成体
想一想
巩固练习
1.下列平面图形绕轴旋转一周,可以得到哪些立体图形?用线连一连
巩固练习
2.下图各个花瓶的表面可以看做由哪个平面图形绕虚线旋转一周而得到?用线连一连.
巩固练习
归纳小结
作业布置
课本第7页,习题1.2,知识技能,1.
情境导入
活动一
观察下面立体图形展开成平面图形的过程.
情境导入
活动二
请你折出自己最拿手的手工折纸.
情境导入
问题
立体图形
展开
平面图形
平面图形
折叠
立体图形
你能分别用一个动词来形容一下刚才的两项活动吗?
第一章
丰富的图形世界
哲觉中学
苏勇
探索新知
在生活中,我们经常见到正方体形状的盒子.
将纸盒完全展开后形状是怎样的?
正方体的11种不同的展开图
探索新知
想一想
将一个正方体的表面沿某些棱剪开,能展成一个平面图形.你能得到哪些平面图形.
探索新知
你能否将得到的平面图形进行分类?你是按什么规律来分类的?
探索新知
第一类:1,4,
1型,共六种.
探索新知
第二类:2,3,
1型,共三种.
探索新知
第三类,2,2,2型,只有一种.
第四类,3,3型,只有一种.
探索新知
能
能
把一个正方体的表面沿某些棱剪开,展成一个平面图形,你能得到下面的平面图形吗?
考考你
下面图形经过折叠能否围成正方体?
能
不能
考考你
一个正方体要将其展开成一个平面图形,必须沿几条棱剪开?
考考你
与1相对的数是2、5、4、6;相对的数是3.
考考你
考考你
归纳小结
这节课你学到了什么?
课本第9页,习题1.3,问题解决,4.
作业布置
作业
情境导入
哲觉中学
苏勇
第一章
丰富的图形世界
棱柱的展开图
展开
探索新知
棱柱的展开图
展开
探索新知
棱柱的展开图
展开
探索新知
以下哪些图形经过折叠可以围成一个棱柱?
⑴
⑵
⑶
⑷
你能将不能围成棱柱的图形作适当修改使其能折叠成棱柱吗?
判断依据:
1、两个底面分居长方形或正方形组(侧面)两端.
2、长方形或正方形组(侧面)个数等于底面边数.
探索新知
把圆柱的侧面展开,会得到什么图形?
探索新知
把圆锥的侧面展开,会得到什么图形?
探索新知
巩固练习
3、
哪种几何体的表面能展开成下面的平面图形?
巩固练习
4、图中的两个图形经过折叠能否围成棱柱?
巩固练习
谈谈你的收获.
归纳小结
课本第11页,习题1.4,知识技能,1.
作业布置
作
业
CT技术以射线作为无形的刀,按照医生选定的方向,对病人的病灶作一系列平行的截面,通过截面图像的解读,医生可以比较精确地得出病灶大小和位置.
你知道CT技术吗?
情境导入
http://www..cn
第一章
丰富的图形世界
用一个平面去截一个几何体,截出的面叫做截面.
截面
探索新知
用一个平面去截一个正方体,截出的面可能是什么形状?
探索新知
探索新知
我们可以看到截面的形状是三角形
探索新知
我们可以看到截面的形状是等腰三角形
探索新知
我们可以看到截面的形状是等边三角形
探索新知
我们可以看到截面的形状是正方形
探索新知
我们可以看到截面的形状是长方形
探索新知
我们可以看到截面的形状是梯形
探索新知
我们可以看到截面的形状是五边形
探索新知
我们可以看到截面的形状是六边形
探索新知
正方形
矩形
梯形
五边形
六边形
三角形
探索新知
n棱柱的截面最多可能是几边形?
(n+2)边形
考考你
用平面去截圆柱体
长方形(正方形)
圆形
其他图形
探索新知
用平面去截圆锥体
圆形
三角形
探索新知
用平面去截球体
圆形
探索新知
1、分别指出图中几何体截面形状的标号.
巩固练习
2、图中各几何体的截面分别是什么形状?
巩固练习
3、用平面去截一个几何体,如果截面的形状是圆,您能想像出原来
的几何体可能是什么吗?如果截面是三角形呢?
巩固练习
谈谈你的收获.
归纳小结
课本第15页,习题1.5,数学理解,3.
作业布置
探索新知
谢
谢!
题西林壁
(宋)苏轼
横看成岭侧成峰,
远近高低各不同,
不识庐山真面目,
只缘身在此山中.
我们从不同的方向观察同一物体时,可能看到不同的图形.
情境导入
第一章
丰富的图形世界
4.
从三个方向看物体的形状
哲觉中学
苏勇
下面的五幅图形,分别是在哪个方向看到的?
请从不同方向观察下图.
正面
右面
左面
后面
上面
探索新知
探索新知
你搭我画
从正面看有几列,每一列有几层?从左面看呢?从上往下看呢?
探索新知
探索新知
两个不同的几何体的三视图可能相同吗?
正方体、球.
考考你
从正面看
从左面看
从上面看
巩固练习
2、画出下图几何体的主视图、左视图、俯视图.
主视图
左视图
俯视图
巩固练习
3、请说出下面三幅图分别是从哪个方向看到的?
左视图
俯视图
主视图
巩固练习
4、请说出下面三幅图分别是从哪个方向看到的?
巩固练习
5、一个小立方块的六面分别标有字母A,B,C,D,E,F.如图是从三个不同方向看到的情形.你能说出A,B,E对面分别是什么字母吗?你是怎么判断的?
巩固练习
一个几何体由几个大小相同的小立方块搭成,从上面看和从左面看所看到的平面图形如图所示.请搭出满足条件的几何体,你搭的几何体由几个小立方块搭成?
探索新知
如图是由几个小立方体块所搭几何体的俯视图,小正方形中的数字表示在该位置小立块的个数,请画出这个几何体的主视图和左视图.
探索新知
如图所示是由几个大小相同的立方块所搭几何体从上面看所看到的平面图形,小正方形中的数字表示在该位置小立方块的个数.请画出相应的几何体从正面看和从左面看所看到的平面图形.
巩固练习
用小立方块搭一个几何体,使得它的主视图和俯视图如图所示.
多少个小立方块?最多需要多少个小立方块?
提高练习
最少摆法中其中之一所需个数:3+2+1+1+1+1+1=10
最多时所需小立方块个数:3+3+3+2+2+2+1=16
提高练习
一个几何体由若干小立方块搭成,它的主视图、左视图和俯视图分别如下,你能搭出相应的几何体吗?
巩固练习
归纳小结
课本第17页,习题1.6,知识技能,1.
作业布置
探索新知
谢谢各位,
再见!
生活中有哪些你熟悉的图形?举例说明.
你喜欢哪些几何体?举出一个生活中的物体,使它尽可能多地包含不同的几何体.
用自己的语言说一说棱柱的特征.
生活中有哪些常见物体可以由平面图形旋转得到?
找出两种几何体,使得分别用一个平面去截它们,可以得到三角形形状的截面.
举出一种几何体,使得它的主视图、左视图和俯视图都一样,你能举出几种?与同伴进行交流.
学完了本章后,你有哪些收获和体会?与同伴进行交流.
用你自己喜欢的方式梳理本章的知识.
回顾与思考
圆柱
圆锥
正方体
长方体
棱柱
球
常见的几何体
圆台
棱锥
回顾与思考
【例1】将下列几何体进行分类?并请说出分类的依据.
按照柱、锥、球分类:
(1)(3)(4)(5)(6)(8)为柱;(2)为锥;(7)为球.
按照有无曲面分类:
(1)(2)(7)有曲面;(3)(4)(5)(6)(8)无曲面.
回顾与思考
【例2】如图所示的几何体各由几个面围成的?面与面相交成几条线?它们是直的还是曲的?
回顾与思考
1、棱柱的侧棱长相等.
2、棱柱的上、下底面相同.
3、棱柱的侧面形状都是长方形.
4、棱柱的侧面个数等于底面边数.
棱柱的特点
回顾与思考
1、两个底面分居长方形或正方形组(侧面)两端.
2、长方形或正方形组(侧面)个数等于底面边数.
怎样判断平面图形是否可以经过折叠围成棱柱?
回顾与思考
【例3】下图中的图形经过折叠后形成哪些立体图形?
长方体
圆锥体
正方体
八棱柱
回顾与思考
一个正方体要剪开多少条棱才能展开成平面图形?一个正方体能展开成多少种平面图形?
回顾与思考
中间四个面 上下各一面
中间三个面
一二隔河见
中间两个面
楼梯天天见
中间没有面
三三连一线
回顾与思考
用一个平面去截正方体,截面可能是哪些形状?
回顾与思考
从上面看
从正面看
从左面看
主视图
左视图
俯视图
几何体的三视图
回顾与思考
【例4】下面是由几个相同立方块组成的几何体的俯视图,小正方形上的数字表示在该位置的小立方块的个数,请画出这个几何体的主视图和左视图.
2
3
2
2
1
主视图
左视图
回顾与思考
【例4】用小立方块搭一个几何体,使它的主视图和俯视图如下图所示,俯视图中的小正方形中的字母表示该位置小立方块的个数,试回答下列问题;
(1)x、z各表示多少?
(2)y可能是多少?这个几何体最少由几个小立块搭成?最多呢?
回顾与思考
1.生活中的立体图形(一)
1.生活中的立体图形(二)
2.展开与折叠(一)
2.展开与折叠(二)
3.截一个几何体
4.从三个方向看物体的形状
回顾与思考
第一章
丰富的图形世界
情境导入
下列图片中有哪些你熟悉的几何体?
情境导入
下列图片中有哪些你熟悉的几何体?
情境导入
下列图片中有哪些你熟悉的几何体?
情境导入
下列图片中有哪些你熟悉的几何体?
情境导入
下列图片中有哪些你熟悉的几何体?
情境导入
下列图片中有哪些你熟悉的几何体?
情境导入
下列图片中有哪些你熟悉的几何体?
1.生活中的立体图形(一)
1.生活中的立体图形(一)
汝州外国语
卢天亮
第一章
丰富的图形世界
找找看
下图中,哪些物体的形状与你在小学学过的几何体类似?
结论
常见的几何体
圆柱
圆锥
正方体
长方体
棱柱
球
棱锥
探索新知
多面体是指各个面都是平面的几何体.
巩固练习
说一说生活中哪些物体的形状分别类似于棱柱、圆柱、圆锥与球.
探索新知
常见几何体都有何特征?
圆柱:底面是圆形,侧面是曲面,只有一个侧面,有两个底面,底面互相平行且相等.
棱柱:底面是多边形,侧面是正方形或长方形,n棱柱有n个侧面,有两个底面,底面互相平行且相等.
圆锥:底面是圆形,侧面是曲面,只有一个侧面和一个底面.
棱锥:底面是多边形,侧面是三角形,有多个侧面.
球:只有一个曲面.
你行吗
请按适当的标准对下列几何体进行分类.
(1)
(2)
(3)
(4)
(5)
(6)
按“柱、锥、球”划分:
(3)(4)(5)是一类,组成它们的面中至少有一个是曲的;(1)(2)(6)一类,组成它们的各面都是平的.
(1)(2)(4)(6)是柱体.(5)是锥体.(3)是球体.
按面的曲或平划分:
探索新知
常见几何体的分类
巩固练习
探索新知
棱柱的侧棱、底面、侧面分别有什么特点?
棱柱的所有侧棱长都相等.
棱柱的上下底面的形状相同.
棱柱的侧面是平行四边形.
认识棱柱
上、下底面是相同的多边形,侧面都是平行四边形的几何图形叫做棱柱
探索新知
棱柱、棱锥是按底面图形的边数来命名的.
考考你
长方形、正方形都是四棱柱.
长方体、正方体是棱柱吗?
探索新知
探索棱柱的特性
棱
柱
顶
点
棱
数
面
数
三棱柱
四棱柱
五棱柱
六棱柱
6
9
5
8
12
6
10
15
7
12
18
8
你能马上说出十棱柱的顶点数、棱数、面数吗?
你能马上说出n棱柱的顶点数、棱数、面数吗?
结论
n棱柱有(n+2)个面,3n条棱,2n个顶点.
探索新知
棱柱有直棱柱和斜棱柱.
本书只讨论直棱柱,简称棱柱
巩固练习
1、一个六棱柱模型如图所示,它的底面边长都是5cm,侧棱长为4cm.观察这个模型,回答下列问题:
(1)这个六棱柱的几个面分别是什么形状?那些面的形状、大小完全相同?
(2)这个六棱柱的所有侧面
的面积之和是多少?
巩固练习
2、圆柱和棱柱有很多相同点,下面的这个几何体与圆柱和棱柱又有什么相同点?
归纳小结
谈谈你的收获.
作业布置
作业
课本第4页,习题1.1,知识技能,1;数学理解,3.
THANK
YOU
!
See
you
next
class!
复习导入
1.
生活中常见的几何体有哪些?你能将它们按一定的标准分类吗?
2.棱柱有些什么性质?
第一章
丰富的图形世界
探索新知
从以上问题中,你能得到什么结论吗?
1.面有平面、曲面之分;线有直线、曲线之分.
2.面与面相交得到线,线与线相交得到点.
探索新知
组成几何图形的基本元素是:点、线、面.
探索新知
观察动画,你发现了什么?
点动成线、线动成面、面动成体
想一想
巩固练习
1.下列平面图形绕轴旋转一周,可以得到哪些立体图形?用线连一连
巩固练习
2.下图各个花瓶的表面可以看做由哪个平面图形绕虚线旋转一周而得到?用线连一连.
巩固练习
归纳小结
作业布置
课本第7页,习题1.2,知识技能,1.
情境导入
活动一
观察下面立体图形展开成平面图形的过程.
情境导入
活动二
请你折出自己最拿手的手工折纸.
情境导入
问题
立体图形
展开
平面图形
平面图形
折叠
立体图形
你能分别用一个动词来形容一下刚才的两项活动吗?
第一章
丰富的图形世界
哲觉中学
苏勇
探索新知
在生活中,我们经常见到正方体形状的盒子.
将纸盒完全展开后形状是怎样的?
正方体的11种不同的展开图
探索新知
想一想
将一个正方体的表面沿某些棱剪开,能展成一个平面图形.你能得到哪些平面图形.
探索新知
你能否将得到的平面图形进行分类?你是按什么规律来分类的?
探索新知
第一类:1,4,
1型,共六种.
探索新知
第二类:2,3,
1型,共三种.
探索新知
第三类,2,2,2型,只有一种.
第四类,3,3型,只有一种.
探索新知
能
能
把一个正方体的表面沿某些棱剪开,展成一个平面图形,你能得到下面的平面图形吗?
考考你
下面图形经过折叠能否围成正方体?
能
不能
考考你
一个正方体要将其展开成一个平面图形,必须沿几条棱剪开?
考考你
与1相对的数是2、5、4、6;相对的数是3.
考考你
考考你
归纳小结
这节课你学到了什么?
课本第9页,习题1.3,问题解决,4.
作业布置
作业
情境导入
哲觉中学
苏勇
第一章
丰富的图形世界
棱柱的展开图
展开
探索新知
棱柱的展开图
展开
探索新知
棱柱的展开图
展开
探索新知
以下哪些图形经过折叠可以围成一个棱柱?
⑴
⑵
⑶
⑷
你能将不能围成棱柱的图形作适当修改使其能折叠成棱柱吗?
判断依据:
1、两个底面分居长方形或正方形组(侧面)两端.
2、长方形或正方形组(侧面)个数等于底面边数.
探索新知
把圆柱的侧面展开,会得到什么图形?
探索新知
把圆锥的侧面展开,会得到什么图形?
探索新知
巩固练习
3、
哪种几何体的表面能展开成下面的平面图形?
巩固练习
4、图中的两个图形经过折叠能否围成棱柱?
巩固练习
谈谈你的收获.
归纳小结
课本第11页,习题1.4,知识技能,1.
作业布置
作
业
CT技术以射线作为无形的刀,按照医生选定的方向,对病人的病灶作一系列平行的截面,通过截面图像的解读,医生可以比较精确地得出病灶大小和位置.
你知道CT技术吗?
情境导入
http://www..cn
第一章
丰富的图形世界
用一个平面去截一个几何体,截出的面叫做截面.
截面
探索新知
用一个平面去截一个正方体,截出的面可能是什么形状?
探索新知
探索新知
我们可以看到截面的形状是三角形
探索新知
我们可以看到截面的形状是等腰三角形
探索新知
我们可以看到截面的形状是等边三角形
探索新知
我们可以看到截面的形状是正方形
探索新知
我们可以看到截面的形状是长方形
探索新知
我们可以看到截面的形状是梯形
探索新知
我们可以看到截面的形状是五边形
探索新知
我们可以看到截面的形状是六边形
探索新知
正方形
矩形
梯形
五边形
六边形
三角形
探索新知
n棱柱的截面最多可能是几边形?
(n+2)边形
考考你
用平面去截圆柱体
长方形(正方形)
圆形
其他图形
探索新知
用平面去截圆锥体
圆形
三角形
探索新知
用平面去截球体
圆形
探索新知
1、分别指出图中几何体截面形状的标号.
巩固练习
2、图中各几何体的截面分别是什么形状?
巩固练习
3、用平面去截一个几何体,如果截面的形状是圆,您能想像出原来
的几何体可能是什么吗?如果截面是三角形呢?
巩固练习
谈谈你的收获.
归纳小结
课本第15页,习题1.5,数学理解,3.
作业布置
探索新知
谢
谢!
题西林壁
(宋)苏轼
横看成岭侧成峰,
远近高低各不同,
不识庐山真面目,
只缘身在此山中.
我们从不同的方向观察同一物体时,可能看到不同的图形.
情境导入
第一章
丰富的图形世界
4.
从三个方向看物体的形状
哲觉中学
苏勇
下面的五幅图形,分别是在哪个方向看到的?
请从不同方向观察下图.
正面
右面
左面
后面
上面
探索新知
探索新知
你搭我画
从正面看有几列,每一列有几层?从左面看呢?从上往下看呢?
探索新知
探索新知
两个不同的几何体的三视图可能相同吗?
正方体、球.
考考你
从正面看
从左面看
从上面看
巩固练习
2、画出下图几何体的主视图、左视图、俯视图.
主视图
左视图
俯视图
巩固练习
3、请说出下面三幅图分别是从哪个方向看到的?
左视图
俯视图
主视图
巩固练习
4、请说出下面三幅图分别是从哪个方向看到的?
巩固练习
5、一个小立方块的六面分别标有字母A,B,C,D,E,F.如图是从三个不同方向看到的情形.你能说出A,B,E对面分别是什么字母吗?你是怎么判断的?
巩固练习
一个几何体由几个大小相同的小立方块搭成,从上面看和从左面看所看到的平面图形如图所示.请搭出满足条件的几何体,你搭的几何体由几个小立方块搭成?
探索新知
如图是由几个小立方体块所搭几何体的俯视图,小正方形中的数字表示在该位置小立块的个数,请画出这个几何体的主视图和左视图.
探索新知
如图所示是由几个大小相同的立方块所搭几何体从上面看所看到的平面图形,小正方形中的数字表示在该位置小立方块的个数.请画出相应的几何体从正面看和从左面看所看到的平面图形.
巩固练习
用小立方块搭一个几何体,使得它的主视图和俯视图如图所示.
多少个小立方块?最多需要多少个小立方块?
提高练习
最少摆法中其中之一所需个数:3+2+1+1+1+1+1=10
最多时所需小立方块个数:3+3+3+2+2+2+1=16
提高练习
一个几何体由若干小立方块搭成,它的主视图、左视图和俯视图分别如下,你能搭出相应的几何体吗?
巩固练习
归纳小结
课本第17页,习题1.6,知识技能,1.
作业布置
探索新知
谢谢各位,
再见!
生活中有哪些你熟悉的图形?举例说明.
你喜欢哪些几何体?举出一个生活中的物体,使它尽可能多地包含不同的几何体.
用自己的语言说一说棱柱的特征.
生活中有哪些常见物体可以由平面图形旋转得到?
找出两种几何体,使得分别用一个平面去截它们,可以得到三角形形状的截面.
举出一种几何体,使得它的主视图、左视图和俯视图都一样,你能举出几种?与同伴进行交流.
学完了本章后,你有哪些收获和体会?与同伴进行交流.
用你自己喜欢的方式梳理本章的知识.
回顾与思考
圆柱
圆锥
正方体
长方体
棱柱
球
常见的几何体
圆台
棱锥
回顾与思考
【例1】将下列几何体进行分类?并请说出分类的依据.
按照柱、锥、球分类:
(1)(3)(4)(5)(6)(8)为柱;(2)为锥;(7)为球.
按照有无曲面分类:
(1)(2)(7)有曲面;(3)(4)(5)(6)(8)无曲面.
回顾与思考
【例2】如图所示的几何体各由几个面围成的?面与面相交成几条线?它们是直的还是曲的?
回顾与思考
1、棱柱的侧棱长相等.
2、棱柱的上、下底面相同.
3、棱柱的侧面形状都是长方形.
4、棱柱的侧面个数等于底面边数.
棱柱的特点
回顾与思考
1、两个底面分居长方形或正方形组(侧面)两端.
2、长方形或正方形组(侧面)个数等于底面边数.
怎样判断平面图形是否可以经过折叠围成棱柱?
回顾与思考
【例3】下图中的图形经过折叠后形成哪些立体图形?
长方体
圆锥体
正方体
八棱柱
回顾与思考
一个正方体要剪开多少条棱才能展开成平面图形?一个正方体能展开成多少种平面图形?
回顾与思考
中间四个面 上下各一面
中间三个面
一二隔河见
中间两个面
楼梯天天见
中间没有面
三三连一线
回顾与思考
用一个平面去截正方体,截面可能是哪些形状?
回顾与思考
从上面看
从正面看
从左面看
主视图
左视图
俯视图
几何体的三视图
回顾与思考
【例4】下面是由几个相同立方块组成的几何体的俯视图,小正方形上的数字表示在该位置的小立方块的个数,请画出这个几何体的主视图和左视图.
2
3
2
2
1
主视图
左视图
回顾与思考
【例4】用小立方块搭一个几何体,使它的主视图和俯视图如下图所示,俯视图中的小正方形中的字母表示该位置小立方块的个数,试回答下列问题;
(1)x、z各表示多少?
(2)y可能是多少?这个几何体最少由几个小立块搭成?最多呢?
回顾与思考
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
