五年级下册数学教案 分数的意义 西师大版
文档属性
| 名称 | 五年级下册数学教案 分数的意义 西师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-30 09:22:07 | ||
图片预览

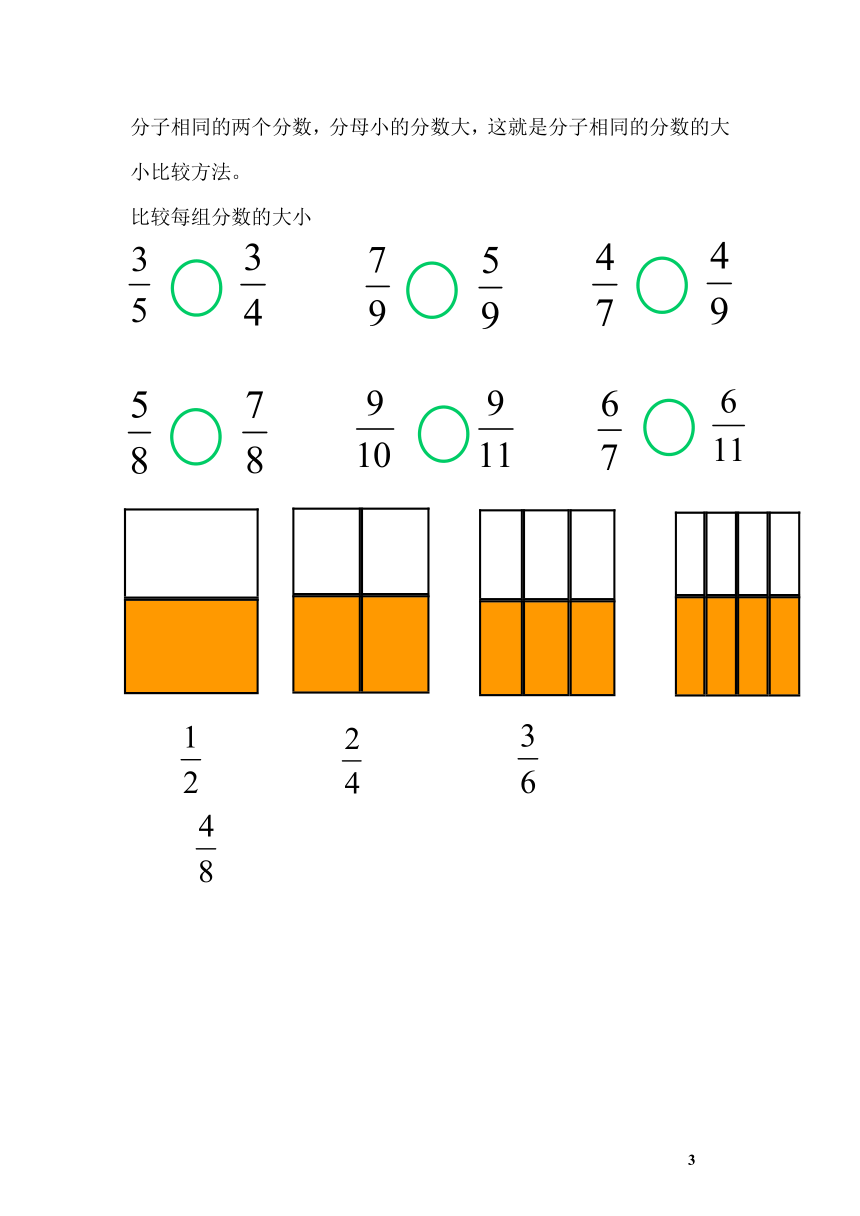

文档简介
分数的意义
教学目标:
掌握分子相同的分数的比较大小方法。
能够运用分数的基本性质把一个数化成分母不同而分数大小不变的分数或者化成指定分母的分数。
经历探究约分和最简分数的意义的过程,理解约分和最简分数的意义。
掌握约分、通分的方法,能正确约分、通分。
探究比较分数大小的方法,能够应用通分的方法比较两个异分母分数的大小。
理解掌握分数与小数互化的方法,能够熟练地进行分数与小数的互化,加深对分数、小数意义的理解。
探究并发现把分数化成有限小数的规律,并能正确判断一个分数能否化成有限小数。
重难点:
会比较分子相同分数的大小,理解在单位“1”相同的情况下,取相同的份数,平均分的份数越少,分数越大。
掌握分数的基本性质,正确应用分数的基本性质。
理解最简分数分意义,掌握约分、通分的方法,能运用分数的基本性质正确约分、通分。
掌握分数与小数互化的方法,能选择合适的方法进行分数与小数互化。
教学过程:
回顾旧知:
一块蛋糕平均分成了10份,每份是这块蛋糕的(
),4份是这块蛋糕的(
)。
里面有几个(
)
。
5个是(
)。
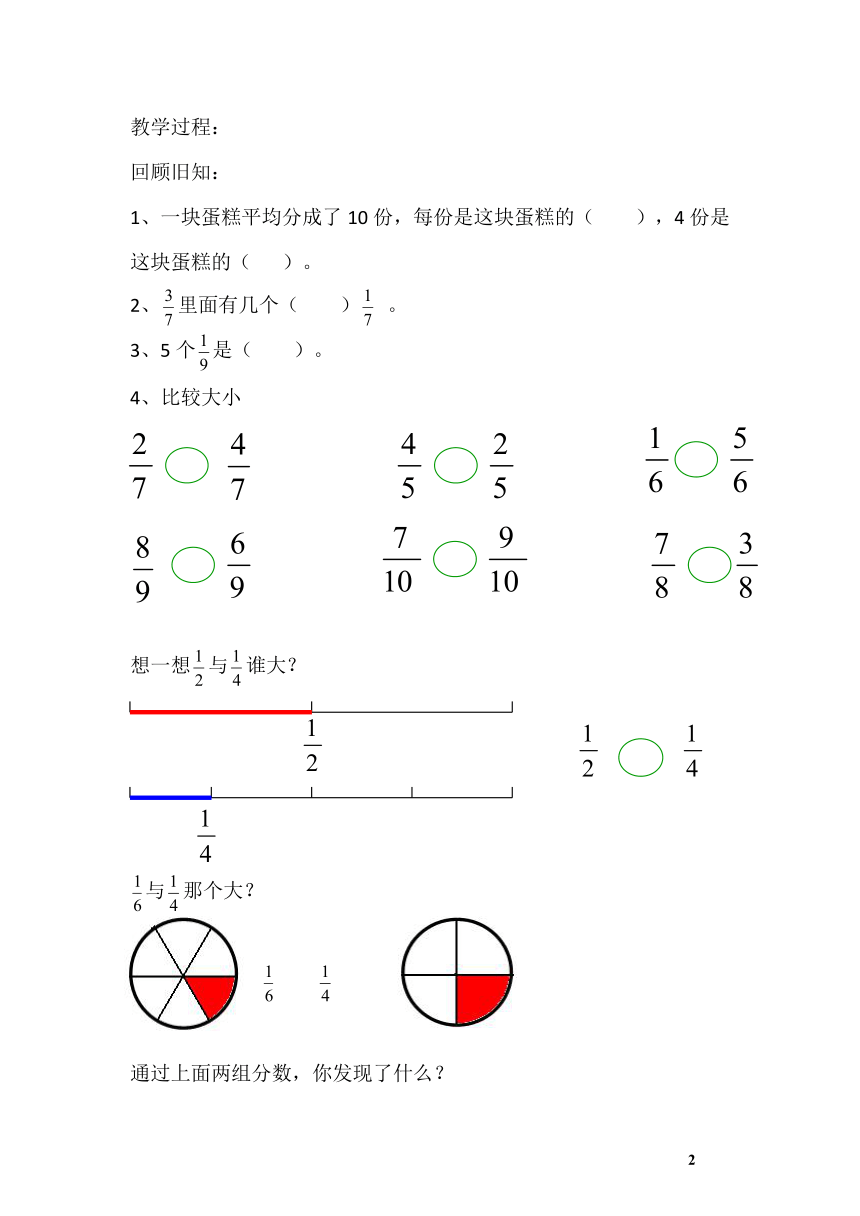
4、比较大小
想一想与谁大?
与那个大?
通过上面两组分数,你发现了什么?
分子相同的两个分数,分母小的分数大,这就是分子相同的分数的大小比较方法。
比较每组分数的大小
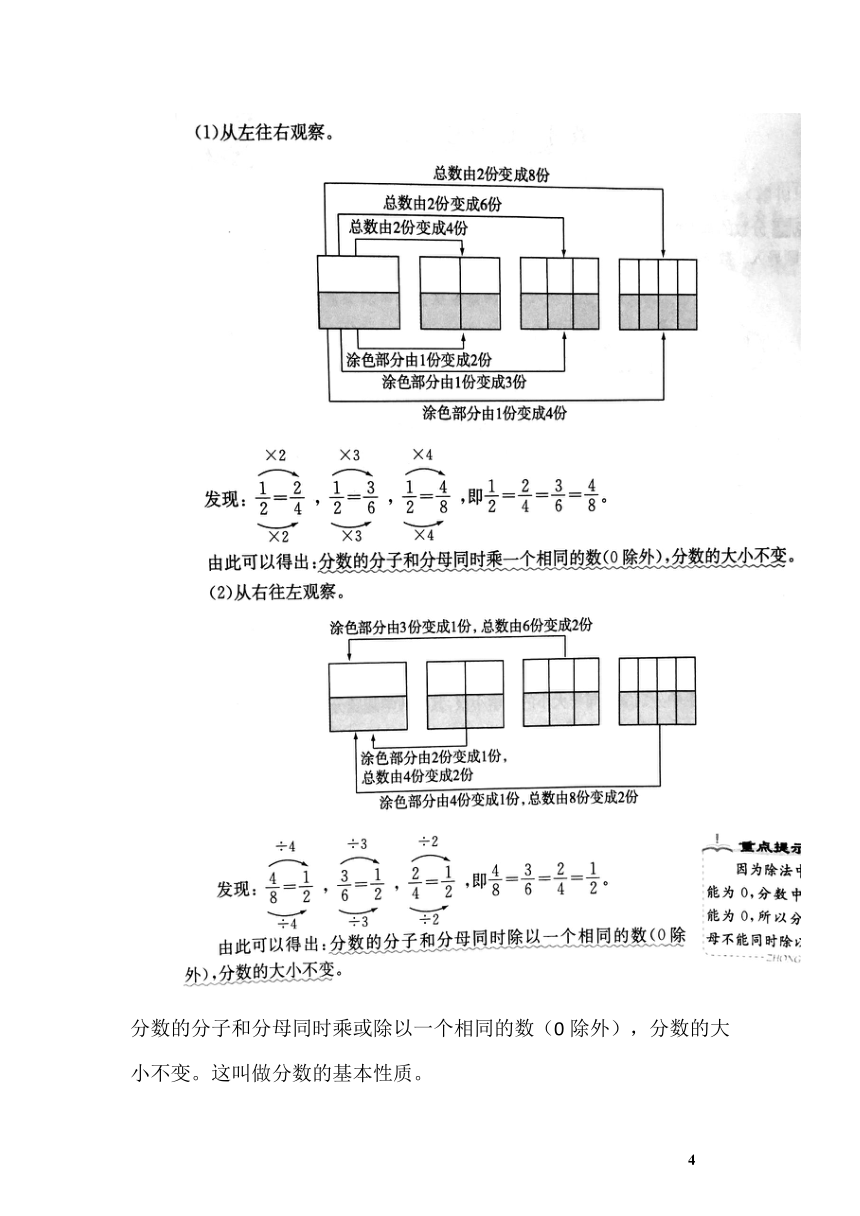
分数的分子和分母同时乘或除以一个相同的数(0除外),分数的大小不变。这叫做分数的基本性质。
下面算式对吗?如果有错,错在哪里?
4.
判断对错,并说明理由。
(1)分数的分子、分母都乘或除以相同的数,分数的大小不变。
(
)
(2)把的分子缩小5倍,分母也同时缩小5倍,分数的大小不变。
(
)
(3)的分子乘3,分母除以3,分数的大小不变。
(
)
还记得什么叫做商不变的性质吗?
3÷4=(
)
÷(4×3)=(
)÷12
想一想:
要把分母24变成8,分母应该除以几?那么分子也应该除以几,分数的大小才不变呢?
=
在下面的括号里填上适当的数。
把
和
化成分母是10而大小不变的分数。
把相等的分数写在同一个圈里。
根据分数的基本性质填空:
求下面各组数的最大公因数。
15和5
7和20
28和42
28的因数有:
42的因数有:
所以28和42的公因数有:
把一个分数化成同它相等,且分子、分母都比原来小的分数的过程是约分。
3
约分的方法及最简分数的意义:
15
1、逐步约分法。
书写格式如:
(在一般情况下,要用分子、分母的公因数
25
(1除外)逐步去除分子、分母。)
3
5
一次约分法。
5
的分子、分母只有公因数1,这样的分数就是最简分数。例如:.........
填空。
一个分数约分后,分数的大小(
)。
的分子和分母的最大公因数是(
),化成最简分数是(
)。
分母是10的所有最简真分数的和是(
)。
一个最简真分数的分子和分母的积是8,这个分数是(
)。
一个最简真分数,分子与分母的和是9,这样的最简真分数有(
)、(
)、和(
)。
约分的技巧:
当分数的分母是分子的整数倍时,约分时分母和分子同时除以分子,约分后的分子是1.
当分数的分母是整十。整百时,约分时可以先划去分子、分母末尾同样多的0,再进行约分。
当分数的分子和分母都是偶数时,可以先用2去除分子、分母,在约分。
运用不变量法解决分数问题。
典型例题:的分子和分母同时加上同一个数,约分后得,分子和分母同时加上的这个数是多少?
(13-5)÷(2-1)=8
8-5=3或16-13=3
运用求差法与分解解决约分问题
典型例题:把化成最简分数。
133-114=19
187-153=34
34÷2=17
比较下面分数的大小。
求下面各组数的最小公倍数。
6和8
15和5
28和42
6的倍数有:
8的倍数有:
所以6和8的公倍数有:
通分的意义:把几个分母不相同的分数,分别化成和原来分数相等并且分母相同的分数的过程是通分。
在通分的过程中,一般情况下选择分母的最小公倍数做分母,这个最小倍数叫做最小公分母。
运用转化法解决分数大小比较问题
典型例题:<<(
)里可以填那些自然数?
运用找中间量法、交叉相乘法解决比较分数大小的问题
典型例题:不通分,你能用其他分方法比较出的大小吗?
方法一:找中间量法。
因为>,<,所以>
方法二:交叉相乘法。
因为5×13>6×8,所以>
1.
填一填
(1)分数的分子相当于除法中的(
),分母相当于(
),分数线相当(
)。如:(
)÷(
)
(2)一位小数表示(
)分之几,两位小数表示(
),三位小数表示(
)……
把化成小数。
3÷4=
11÷25=
23÷8=
观察,他们有什么特点
这三个分数都是最简分数,并且都能化成有限小数。
4、25和8分别是这三个最简分数的分母,把他们分解质因数。
4=2×2
25=5×5
8=2×2×2
得出:一个最简分数,如果分母中只含有质因数2或5(2和5),这个分数就能化成有限小数。
想一想,如果一个最简分数的分母中除了含有质因数2或5(2和5)以外,还能不能化为有限小数。
如:
一个最简分数,如果分母中除了含有质因数2或5(2和5)以外,还有其他的质因数,那么这个分数就不能化成有限小数。
把小数化成分数的方法。
规律:把小数化成分数,有几位小数,就在1的后面写几个0作分母,把小数的小数点去掉作分子,再通过约分把不是最简分数的化成最简分数。
分数与小数互化的实际应用
小华栽了两棵果树,梨树高0.8m苹果树高m。那棵树高一些?
把分数化成小数比较
=7÷8=
把小数化成分数比较。
0.8==
比较分数和小数的大小时,可以吧小数化成分数后再比较,也可以先把分数化成小数后再比较。
把下面的分数化成小数或整数。(除不尽的保留两位小数)
把下面的小数化成分数
0.23
2.369
8.1
0.88
4.6
0.65
3判断。
不能化成有限小数。
(
)
10.7化成分数是。
(
)
分母是整十,整百的分数都能化成有限小数。
(
)
假分数的分子一定比分母大。
(
)
约分和通分的依据都是分数的基本性质。
(
)
12
1
教学目标:
掌握分子相同的分数的比较大小方法。
能够运用分数的基本性质把一个数化成分母不同而分数大小不变的分数或者化成指定分母的分数。
经历探究约分和最简分数的意义的过程,理解约分和最简分数的意义。
掌握约分、通分的方法,能正确约分、通分。
探究比较分数大小的方法,能够应用通分的方法比较两个异分母分数的大小。
理解掌握分数与小数互化的方法,能够熟练地进行分数与小数的互化,加深对分数、小数意义的理解。
探究并发现把分数化成有限小数的规律,并能正确判断一个分数能否化成有限小数。
重难点:
会比较分子相同分数的大小,理解在单位“1”相同的情况下,取相同的份数,平均分的份数越少,分数越大。
掌握分数的基本性质,正确应用分数的基本性质。
理解最简分数分意义,掌握约分、通分的方法,能运用分数的基本性质正确约分、通分。
掌握分数与小数互化的方法,能选择合适的方法进行分数与小数互化。
教学过程:
回顾旧知:
一块蛋糕平均分成了10份,每份是这块蛋糕的(
),4份是这块蛋糕的(
)。
里面有几个(
)
。
5个是(
)。
4、比较大小
想一想与谁大?
与那个大?
通过上面两组分数,你发现了什么?
分子相同的两个分数,分母小的分数大,这就是分子相同的分数的大小比较方法。
比较每组分数的大小
分数的分子和分母同时乘或除以一个相同的数(0除外),分数的大小不变。这叫做分数的基本性质。
下面算式对吗?如果有错,错在哪里?
4.
判断对错,并说明理由。
(1)分数的分子、分母都乘或除以相同的数,分数的大小不变。
(
)
(2)把的分子缩小5倍,分母也同时缩小5倍,分数的大小不变。
(
)
(3)的分子乘3,分母除以3,分数的大小不变。
(
)
还记得什么叫做商不变的性质吗?
3÷4=(
)
÷(4×3)=(
)÷12
想一想:
要把分母24变成8,分母应该除以几?那么分子也应该除以几,分数的大小才不变呢?
=
在下面的括号里填上适当的数。
把
和
化成分母是10而大小不变的分数。
把相等的分数写在同一个圈里。
根据分数的基本性质填空:
求下面各组数的最大公因数。
15和5
7和20
28和42
28的因数有:
42的因数有:
所以28和42的公因数有:
把一个分数化成同它相等,且分子、分母都比原来小的分数的过程是约分。
3
约分的方法及最简分数的意义:
15
1、逐步约分法。
书写格式如:
(在一般情况下,要用分子、分母的公因数
25
(1除外)逐步去除分子、分母。)
3
5
一次约分法。
5
的分子、分母只有公因数1,这样的分数就是最简分数。例如:.........
填空。
一个分数约分后,分数的大小(
)。
的分子和分母的最大公因数是(
),化成最简分数是(
)。
分母是10的所有最简真分数的和是(
)。
一个最简真分数的分子和分母的积是8,这个分数是(
)。
一个最简真分数,分子与分母的和是9,这样的最简真分数有(
)、(
)、和(
)。
约分的技巧:
当分数的分母是分子的整数倍时,约分时分母和分子同时除以分子,约分后的分子是1.
当分数的分母是整十。整百时,约分时可以先划去分子、分母末尾同样多的0,再进行约分。
当分数的分子和分母都是偶数时,可以先用2去除分子、分母,在约分。
运用不变量法解决分数问题。
典型例题:的分子和分母同时加上同一个数,约分后得,分子和分母同时加上的这个数是多少?
(13-5)÷(2-1)=8
8-5=3或16-13=3
运用求差法与分解解决约分问题
典型例题:把化成最简分数。
133-114=19
187-153=34
34÷2=17
比较下面分数的大小。
求下面各组数的最小公倍数。
6和8
15和5
28和42
6的倍数有:
8的倍数有:
所以6和8的公倍数有:
通分的意义:把几个分母不相同的分数,分别化成和原来分数相等并且分母相同的分数的过程是通分。
在通分的过程中,一般情况下选择分母的最小公倍数做分母,这个最小倍数叫做最小公分母。
运用转化法解决分数大小比较问题
典型例题:<<(
)里可以填那些自然数?
运用找中间量法、交叉相乘法解决比较分数大小的问题
典型例题:不通分,你能用其他分方法比较出的大小吗?
方法一:找中间量法。
因为>,<,所以>
方法二:交叉相乘法。
因为5×13>6×8,所以>
1.
填一填
(1)分数的分子相当于除法中的(
),分母相当于(
),分数线相当(
)。如:(
)÷(
)
(2)一位小数表示(
)分之几,两位小数表示(
),三位小数表示(
)……
把化成小数。
3÷4=
11÷25=
23÷8=
观察,他们有什么特点
这三个分数都是最简分数,并且都能化成有限小数。
4、25和8分别是这三个最简分数的分母,把他们分解质因数。
4=2×2
25=5×5
8=2×2×2
得出:一个最简分数,如果分母中只含有质因数2或5(2和5),这个分数就能化成有限小数。
想一想,如果一个最简分数的分母中除了含有质因数2或5(2和5)以外,还能不能化为有限小数。
如:
一个最简分数,如果分母中除了含有质因数2或5(2和5)以外,还有其他的质因数,那么这个分数就不能化成有限小数。
把小数化成分数的方法。
规律:把小数化成分数,有几位小数,就在1的后面写几个0作分母,把小数的小数点去掉作分子,再通过约分把不是最简分数的化成最简分数。
分数与小数互化的实际应用
小华栽了两棵果树,梨树高0.8m苹果树高m。那棵树高一些?
把分数化成小数比较
=7÷8=
把小数化成分数比较。
0.8==
比较分数和小数的大小时,可以吧小数化成分数后再比较,也可以先把分数化成小数后再比较。
把下面的分数化成小数或整数。(除不尽的保留两位小数)
把下面的小数化成分数
0.23
2.369
8.1
0.88
4.6
0.65
3判断。
不能化成有限小数。
(
)
10.7化成分数是。
(
)
分母是整十,整百的分数都能化成有限小数。
(
)
假分数的分子一定比分母大。
(
)
约分和通分的依据都是分数的基本性质。
(
)
12
1
