【备战2021年中考数学几何模型汇编专练】专题四 手拉手模型 复习教案
文档属性
| 名称 | 【备战2021年中考数学几何模型汇编专练】专题四 手拉手模型 复习教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-30 10:16:15 | ||
图片预览




文档简介
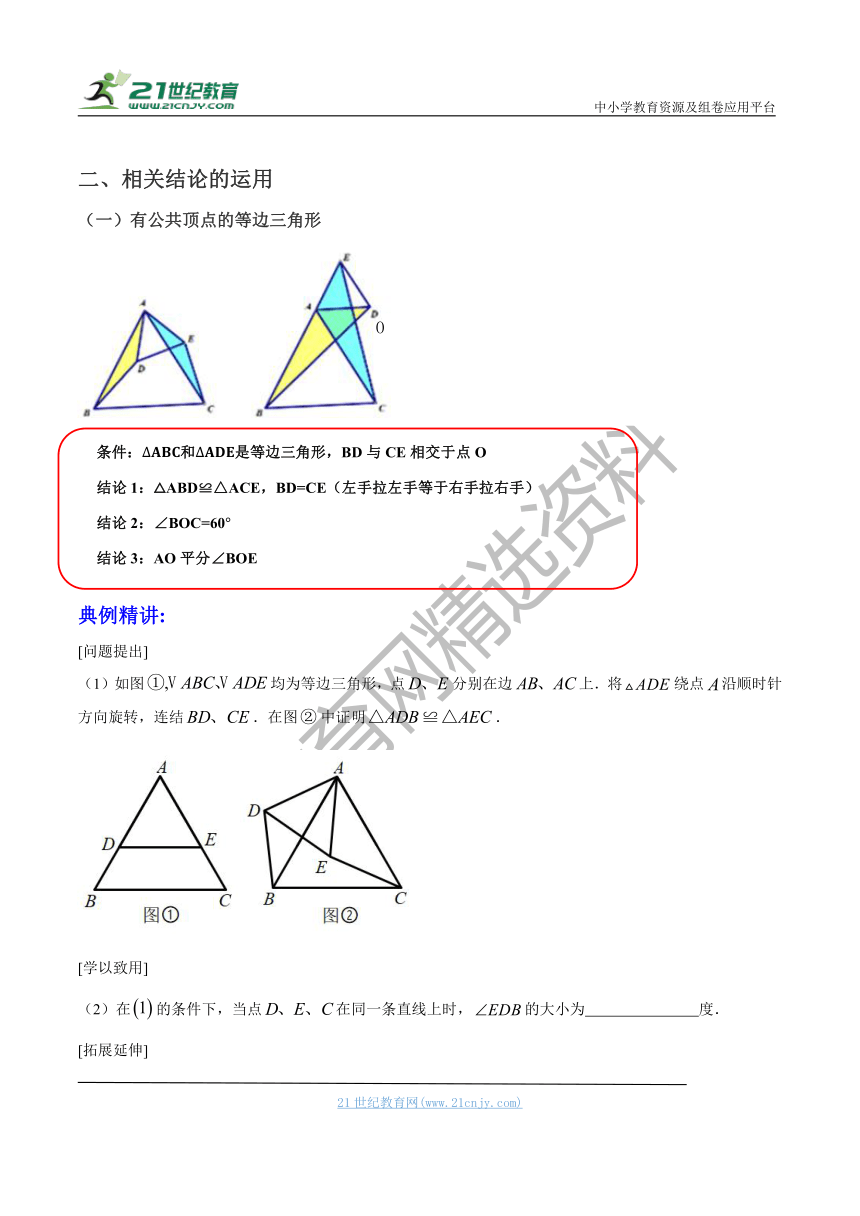
数学模型-----手拉手
有些同学在学习数学时无从下手,找不到突破的方法,做不到举一反三,所以在数学的学习过程中,必须深入本质,做到知识、规律、法则掌握准确,及时反思。下面先给大家介绍一种常见的数学模型---手拉手模型,通过对模型的理解和掌握,把模型的结论融会贯通,理解透彻,那么这一类题型,都是可以迎刃而解的。
一、模型类别
二、相关结论的运用
(一)有公共顶点的等边三角形
2524125637540O
O
-169545247656858026670条件:?ABC和?ADE是等边三角形,BD与CE相交于点O
结论1:△ABD≌△ACE,BD=CE(左手拉左手等于右手拉右手)
结论2:∠BOC=60°
结论3:AO平分∠BOE
条件:?ABC和?ADE是等边三角形,BD与CE相交于点O
结论1:△ABD≌△ACE,BD=CE(左手拉左手等于右手拉右手)
结论2:∠BOC=60°
结论3:AO平分∠BOE
典例精讲:
[问题提出]
(1)如图false均为等边三角形,点false分别在边false上.将false绕点false沿顺时针方向旋转,连结false.在图false中证明false.
4650105103505
[学以致用]
(2)在false的条件下,当点false在同一条直线上时,false的大小为 度.
[拓展延伸]
(3)在false的条件下,连结false.若false直接写出false的面积false的取值范围.
【思路点拨】
(1)根据“手拉手”模型1,证明false即可;
(2)分“当点false在线段false上”和“当点false在线段false的延长线上”两种情况,再根据“手拉手”模型1中的结论2即可求得false的大小;
(3)分别求出false的面积最大值和最小值即可得到结论
【详解】
(1)false均为等边三角形,
false,false,
false,
即false
在false和false中
false
false;
(2)当false在同一条直线上时,分两种情况:
①当点false在线段false上时,如图,
∵false是等边三角形,
false,
false,
由(1)可知,false,
false,
false
②当点false在线段false的延长线上时,如图,
false是等边三角形,
false
false,
由(1)可知,false
false,
false false
综上所述,false的大小为false或false
(3)过点A作false于点F,当点D在线段AF上时,点D到BC的距离最短,此时,点D到BC的距离为线段DF的长,如图:
false是等边三角形,false,false
false,false
false
false
此时false;
当D在线段FA的延长线上时,点D到BC的距离最大,此时点D到BC的距离为线段DF的长,如图,
false是等边三角形,false,false
false,false,
false
false
false
此时,false;
综上所述,false的面积S 取值是false
【解题技法】 “手拉手”模型1中,对应边“拉手线”组成的两个三角形全等
实战演练:
1.(1)如图1,已知△CAB和△CDE均为等边三角形,D在AC上,E在CB上,易得线段AD和BE的数量关系是 .
(2)将图1中的△CDE绕点C旋转到图2的位置,直线AD和直线BE交于点F.
①判断线段AD和BE的数量关系,并证明你的结论;
②图2中∠AFB的度数是 .
(3)如图3,若△CAB和△CDE均为等腰直角三角形,∠ABC=∠DEC=90°,AB=BC,DE=EC,直线AD和直线BE交于点F,分别写出∠AFB的度数,线段AD、BE间的数量关系.
(二)有公共顶点的等腰直角三角形
26860572390条件:?ABC和?ADE是等腰直角三角形,BD与CE相交于点O
结论1:△ABD≌△ACE,BD=CE(左手拉左手等于右手拉右手)
结论2:∠BOC=90°
结论3: AO平分∠BOE
条件:?ABC和?ADE是等腰直角三角形,BD与CE相交于点O
结论1:△ABD≌△ACE,BD=CE(左手拉左手等于右手拉右手)
结论2:∠BOC=90°
结论3: AO平分∠BOE
8763071120
典例精讲:
如图,△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=α,AC、BD交于M
(1)如图1,当α=90°时,∠AMD的度数为 °
(2)如图2,当α=60°时,∠AMD的度数为 °
(3)如图3,当△OCD绕O点任意旋转时,∠AMD与α是否存在着确定的数量关系?如果存在,请你用表示∠AMD,并图3进行证明;若不确定,说明理由.
【思路点拨】
(1)如图1中,设OA交BD于K.根据“手拉手”模型2证明△BOD≌△AOC,推出∠OBD=∠OAC,由∠AKM=∠BKO,可得∠AMK=∠BOK=90°;
(2)如图2中,设OA交BD于K.根据“手拉手”模型1证明△BOD≌△AOC,推出∠OBD=∠OAC,由∠AKM=∠BKO,推出∠AMK=∠BOK=60°;
(3)如图3中,设OA交BD于K.根据“手拉手”模型3证明△BOD≌△AOC,根据“手拉手”模型中的结论2可得∠AMD=180°-α.
【详解】
(1)如图1中,设OA交BD于K.
∵OA=OB,OC=OD,∠AOB=∠COD=α,
∴∠BOD=∠AOC,∴△BOD≌△AOC,
∴∠OBD=∠OAC,
∵∠AKM=∠BKO,∴∠AMK=∠BOK=90°.
故答案为90.
(2)如图2中,设OA交BD于K.
∵OA=OB,OC=OD,∠AOB=∠COD=α,
∴∠BOD=∠AOC,
∴△BOD≌△AOC,∴∠OBD=∠OAC,
∵∠AKM=∠BKO,∴∠AMK=∠BOK=60°.
故答案为60.
(3)如图3中,设OA交BD于K.
∵OA=OB,OC=OD,∠AOB=∠COD=α,
∴∠BOD=∠AOC,∴△BOD≌△AOC,
∴∠OBD=∠OAC,
∵∠AKO=∠BKM,∴∠AOK=∠BMK=α.
∴∠AMD=180°﹣α.
【解题技法】“手拉手”模型2中,两条“拉手线”所在直线的夹角与初始图形中公共顶点对应的角相等或互补
实战演练:
1.已知:如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点E在BC边上.
(1)求证:△ACD≌△ABE;
(2)若∠CDE=60°,求∠AEB的度数.
2.△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°
(1)如图1,点D,E在AB,AC上,则BD,CE满足怎样的数量关系和位置关系?
(2)如图2,点D在△ABC内部,点E在△ABC外部,连结BD,CE,则BD,CE满足怎样的数量关系和位置关系?请说明理由.
(3)如图3,点D,E都在△ABC外部,连结BD,CE,CD,EB,BD与CE相交于F点.
①若BD=4,求四边形BCDE的面积.
②若AB=2,AD=1,设CD2=x,EB2=y,求y与x之间的函数关系式.
3. 如图乙,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)如图甲,将△ADE绕点A旋转,当C、D、E在同一条直线上时,连接BD、BE,则下列给出的四个结论中,其中正确的是哪几个 .(回答直接写序号)
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2)
(2)若AB=6,AD=3,把△ADE绕点A旋转:
①当∠CAE=90°时,求PB的长;
②直接写出旋转过程中线段PB长的最大值和最小值.
(三)顶角相等的等腰三角形
7810572390条件:?ABC和?ADE是等腰三角形,且∠BAC =∠DAE ,BD与CE相交于点O
结论1:△ABD≌△ACE,BD=CE(左手拉左手等于右手拉右手)
结论2:∠BOC=∠BAC
结论3: AO平分∠BOE
条件:?ABC和?ADE是等腰三角形,且∠BAC =∠DAE ,BD与CE相交于点O
结论1:△ABD≌△ACE,BD=CE(左手拉左手等于右手拉右手)
结论2:∠BOC=∠BAC
结论3: AO平分∠BOE
190572390
典例精讲:
观察猜想
如图1,有公共直角顶点false的两个不全等的等腰直角三角尺叠放在一起,点false在false上,点false在false上.
(1)在图1中,你发现线段false,false的数量关系是___________,直线false,false的位置关系是________.
操作发现
(2)将图1中的false绕点false逆时针旋转一个锐角得到图2,这时(1)中的两个结论是否成立?作出判断并说明理由;
拓广探索
(3)如图3,若只把“有公共直角顶点false的两个不全等的等腰直角三角尺”改为“有公共顶角为false(锐角)的两个不全等等腰三角形”,false绕点false逆时针旋转任意一个锐角,这时(1)中的两个结论仍然成立吗?作出判断,不必说明理由.
(1)false,false;(2)将图1中的false绕点false逆时针旋转一个锐角时,两个结论成立.理由见解析;(3)结论false成立;结论false不成立.
【思路点拨】
(1)根据△ABC和△ADE是等腰直角三角形,得到AB=AC,AD=AE,∠A=90°,即可得出结论;
(2)由旋转的性质得到∠DAB=∠EAC.根据“手拉手”模型2证明△ABD≌△ACE,得出BD=CE.再根据“手拉手”模型2的结论2可得出false.
(3)根据“手拉手”模型3证明△ABD≌△ACE,可得BD=CE成立,再根据“手拉手”模型3的结论2可得出BD⊥CE不成立.
【详解】
(1)∵△ABC和△ADE是等腰直角三角形,∴AB=AC,AD=AE,∠A=90°,∴BD=CE,BD⊥CE.
故答案为:BD=CE,BD⊥CE.
(2)将图1中的△ABC绕点A逆时针旋转一个锐角时,两个结论成立.理由如下:
由旋转得:∠DAB=∠EAC.
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS).
∴BD=CE.
如图,延长DB,交CE于点F,交AE于点O.
∵△ABD≌△ACE,
∴∠ADB=∠AEC.
∵∠AOD=∠EOF.
∴∠OFE=∠OAD.
∵∠OAD=90°,
∴∠DFE=90°,即BD⊥CE.
(3)结论BD=CE成立,结论BD⊥CE不成立.理由如下:
由旋转得:∠DAE=∠BAC,
∴∠DAB=∠EAC.
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS).
∴BD=CE.
延长DB交CE于M,BD与AE交于点N.
∵△ABD≌△ACE,∴∠MEA=∠BDA.
∵∠ENM=∠DNA,∴∠EMN=∠EAD.
∵∠EAD≠90°,∴∠EMN≠90°,∴BD⊥CE不成立.
【解题技法】对于以等腰三角形的顶点为旋转点,进行适当旋转的题目,连接对应点构造新的三角形,根据“手拉手”模型3证明三角形全等即可解决问题
实战演练:
1、如图,在false中,false,D、E分别是false、false的中点,false.
(1)如图12-1,若false,求false的长度(用含a的代数式表示);
(2)如图12-2,将false绕点A顺时针旋转,旋转角为false,连接false、false,判断false与false的数量关系,并说明理由;
(3)在(2)的条件下,当false的外心在三角形的外部时,请直接写出false的取值范围.
2、如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE,CF相交于点D,
(1)求证:BE=CF ;
(2)当四边形ACDE为菱形时,求BD的长.
(四)有公共顶点的正方形
-102870137985519051437005条件:正方形ABCD和正方形CEFG, BD与CE相交于点O
结论1:△BCE≌△DCE,BE=DG(左手拉左手等于右手拉右手)
结论2:∠BOG=90°
结论3: CO平分∠BOG
条件:正方形ABCD和正方形CEFG, BD与CE相交于点O
结论1:△BCE≌△DCE,BE=DG(左手拉左手等于右手拉右手)
结论2:∠BOG=90°
结论3: CO平分∠BOG
典例精讲:
规定:有一角重合,且角的两边叠合在一起的两个相似四边形叫做“嵌套四边形”,如图,四边形ABCD和AMPN就是嵌套四边形.
(1)问题联想
如图①,嵌套四边形ABCD,AMPN都是正方形,现把正方形AMPN以A为中心顺时针旋转150°得到正方形AM'P'N',连接BM',DN'交于点O,则BM'与DN'的数量关系为_____,位置关系为_____;
(2)类比探究
如图②,将(1)中的正方形换成菱形,∠BAD=∠MAN=60,其他条件不变,则(1)中的结论还成立吗? 若成立,请说明理由;若不成立,请给出正确的结论,并说明理由;
(3)拓展延伸
如图3,将(1)中的嵌套四边形ABCD和AMPN换成是长和宽之比为2:1的矩形,旋转角换成α(90°<α<180°),其他条件不变,请直接写出BM'与DN'的数量关系和位置关系.
【思路点拨】
(1)根据“手拉手”模型4证明△ABM’≌△AND’,得到false,再根据“手拉手”模型4的结论2得出false;
(2)根据“手拉手”模型4和菱形的性质证明false,再推false,故可求解;
(3)根据“手拉手”模型4和矩形的性质证明false,得到false,再推出false即可求解.
【详解】
(1)如图设false,false交于点H,,
∵四边形ABCD,AMPN都是正方形,把正方形AMPN以A为中心顺时针旋转150°得到正方形AM'P'N',
∴AB=AD,AM’=AD’, false
∴△ABM’≌△AND’,
∴false,∠ABM’=∠ADN’,
∵∠ADN’+∠DHA+∠DAH=180°,∠ABM’+∠BHO+∠BOD=180°,
又∠DHA=∠BHO
∴false,即false
故答案为:false,false;
(2)false成立,false不成立,false与false相交,且夹角为false.
理由:设false,false交于点false,
由旋转的性质可得false.
∵四边形false,false都是菱形,
∴false,false,
∴false,
∴false,false.
又∵false,
∴false;
故false与false相交,且夹角为false;
(3)false,false,理由如下:
设false,false交于点false,
由旋转的性质可得false.
∵四边形ABCD和AMPN是长和宽之比为2:1的矩形
∴false,false,
∴false
∴false,
∴false,false.
又∵false,
∴false
∴false,false.
【解题技法】利用“手拉手”模型4证明三角形全等,再把特殊情况推广到一般情况,再运用类比的思想方法是一种常用的数学方法.
实战演练:
(1)在正方形ABCD中,G是CD边上的一个动点(不与C、D重合),以CG为边在正方形ABCD外作一个正方形CEFG,连结BG、DE,如图①.直接写出线段BG、DE的关系 ;
(2)将图①中的正方形CEFG绕点C按顺时针方向旋转任意角度false,如图②,试判断(1)中的结论是否成立?若成立,直接写出结论,若不成立,说明理由;
(3)将(1)中的正方形都改为矩形,如图③,再将矩形CEFG绕点C按顺时针方向旋转任意角度false,如图④,若AB=a,BC=b;CE =ka,CG=kb,(false)试判断(1)中的结论是否仍然成立?并说明理由.
(五)有公共顶点的直角三角形
190533020条件:CD//AB,且∠AOB =∠COD=90° ,BD与CA相交于点E
结论1:△AOC~△BOD
结论2: false
结论3: 四边形ABCD的面积=12AC.BD
条件:CD//AB,且∠AOB =∠COD=90° ,BD与CA相交于点E
结论1:△AOC~△BOD
结论2: false
结论3: 四边形ABCD的面积=12AC.BD
-13144536195
典例精讲:
1.(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①false的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断false的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=false,请直接写出当点C与点M重合时AC的长.
【思路点拨】
(1)①根据“手拉手”模型3证明△COA≌△DOB,得AC=BD;
②根据“手拉手”模型3的结论2得出∠AMB=∠AOB;
(2)根据“手拉手”模型5证明△AOC∽△BOD,则false,再根据“手拉手”模型5的结论2得出∠AMB的度数;
(3)正确画图形,当点C与点M重合时,有两种情况,如图3和4,根据在旋转过程中,始终有 “手拉线”AC与BD垂直,据此设出未知数,运用勾股定理求解即可.
【详解】
(1)问题发现:
①如图1,
∵∠AOB=∠COD=40°,∴∠COA=∠DOB,
∵OC=OD,OA=OB,∴△COA≌△DOB(SAS),
∴AC=BD,∴false
②∵△COA≌△DOB,∴∠CAO=∠DBO,
∵∠AOB=40°,∴∠OAB+∠ABO=140°,
在△AMB中,∠AMB=180°-(∠CAO+∠OAB+∠ABD)=180°-(∠DBO+∠OAB+∠ABD)=180°-140°=40°,
(2)类比探究:
如图2,false,∠AMB=90°,理由是:
Rt△COD中,∠DCO=30°,∠DOC=90°,
∴false,
同理得:false,
∴false, ∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD,∴△AOC∽△BOD,
∴false ,∠CAO=∠DBO,
在△AMB中,∠AMB=180°-(∠MAB+∠ABM)=180°-(∠OAB+∠ABM+∠DBO)=90°;
(3)拓展延伸:
①点C与点M重合时,如图3,
同理得:△AOC∽△BOD,∴∠AMB=90°,false,
设BD=x,则AC=falsex,
Rt△COD中,∠OCD=30°,OD=1,
∴CD=2,BC=x-2,
Rt△AOB中,∠OAB=30°,OB=false,
∴AB=2OB=2false,
在Rt△AMB中,由勾股定理得:AC2+BC2=AB2,
(falsex)2+(x?2)2=(2false)2,
x2-x-6=0,
(x-3)(x+2)=0,
x1=3,x2=-2,
∴AC=3false;
②点C与点M重合时,如图4,
同理得:∠AMB=90°,false,
设BD=x,则AC=falsex,
在Rt△AMB中,由勾股定理得:AC2+BC2=AB2,
(falsex)2+(x+2)2=(2false)2.
x2+x-6=0,
(x+3)(x-2)=0,
x1=-3,x2=2,
∴AC=2false;.
综上所述,AC的长为3false或2false.
【解题技法】用运动和变化的眼光观察和研究图形,把握图形旋转过程中的等量关系,抓住利用“手拉手”模型5得出△AOC∽△BOD是解题的关键.
实战演练:
1、如图1,在Rt△ABC中,∠B=90°,AB=4,BC=2,点D、E分别是边BC、AC的中点,连接DE.将△CDE绕点C逆时针方向旋转,记旋转角为α.
(1)问题发现
①当α=0°时,false=_______;
②当α=180°时,false=______.
(2)拓展探究
试判断:当0°≤α<360°时,false的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
△CDE绕点C逆时针旋转至A、B、E三点在同一条直线上时,求线段BD的长.
2、如图(1),在false中,false,点false分别是边false的中点,连接false.
(1)如图①,求false的值;
(2)将false绕点false顺时针旋转到如图(2)的位置时,false的大小是否发生变化,若不变化,请说明理由;若发生变化,请求出它的值;
(3)将false绕点false顺时针旋转到直线false的下方,且false在同一直线上时,如图(3),求线段false的长.
(六)有公共顶点的任意三角形
306705296545条件:CD//AB,BD与CA相交于点E
结论1:△AOC~△BOD
结论2: ∠AEB =∠COD=∠AOB
结论3: 点E在△BOA的外接圆上
条件:CD//AB,BD与CA相交于点E
结论1:△AOC~△BOD
结论2: ∠AEB =∠COD=∠AOB
结论3: 点E在△BOA的外接圆上
154305-52705
典例精讲:
在false,false,false.点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.
(1)观察猜想
如图1,当false时,false的值是 ,直线BD与直线CP相交所成的较小角的度数是 .
(2)类比探究
如图2,当false时,请写出false的值及直线BD与直线CP相交所成的小角的度数,并就图2的情形说明理由.
(3)解决问题
当false时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时false的值.
【思路点拨】
(1)如图1中,延长CP交BD的延长线于E,设AB交EC于点O.根据“手拉手”模型1证明false,得出CP=BD,.根据“手拉手”模型1的结论2即可解决问题.
(2)如图2中,设BD交AC于点O,BD交PC于点E.根据“手拉手”模型6证明false,得出false即可解决问题.
(3)分两种情形:①如图3﹣1中,当点D在线段PC上时,延长AD交BC的延长线于H.证明false即可解决问题.
②如图3﹣2中,当点P在线段CD上时,同法可证:false解决问题.
【详解】
解:(1)如图1中,延长CP交BD的延长线于E,设AB交EC于点O.
false,
false,
false,false,
false,
false,false,
false,
false,
false,线BD与直线CP相交所成的较小角的度数是false,
故答案为1,false.
(2)如图2中,设BD交AC于点O,BD交PC于点E.
false,
false,
false,
false,
false,false,
false,
false,
false直线BD与直线CP相交所成的小角的度数为false.
(3)如图3﹣1中,当点D在线段PC上时,延长AD交BC的延长线于H.
false,false,
false,
false,
false,
false,
false,
false,
false,false,
false,
false,
false,
false,
false,
false,
false,
false,
false,
falseA,D,C,B四点共圆,
false,false,
false,
false,设false,则false,false,
falsec.
如图3﹣2中,当点P在线段CD上时,同法可证:false,设false,则false,false,
false,
false.
【解题技法】“手拉手”模型中,对应边和“拉手线”组成的两个三角形相似,学会根据题干的条件灵活运用,运用分类讨论的数学思想思考问题.
实战演练:
在false中,false,false是平面内不与点false重合的任意一点,连接false,将线段false绕点false顺时针旋转false得到线段false,连接false是false的中点,false是false的中点.
(1)问题发现:
如图1,当false时,false的值是_________,直线false与直线false相交所成的较小角的度数是________.
(2)类比探究:
如图2,当false时,请写出false的值及直线false与直线false相交所成的较小角的度数,并说明理由.
(3)解决问题:
如图3,当false时,若false是false的中点,点false在直线false上,且点false在同一条直线上,请直接写出false的值.
有些同学在学习数学时无从下手,找不到突破的方法,做不到举一反三,所以在数学的学习过程中,必须深入本质,做到知识、规律、法则掌握准确,及时反思。下面先给大家介绍一种常见的数学模型---手拉手模型,通过对模型的理解和掌握,把模型的结论融会贯通,理解透彻,那么这一类题型,都是可以迎刃而解的。
一、模型类别
二、相关结论的运用
(一)有公共顶点的等边三角形
2524125637540O
O
-169545247656858026670条件:?ABC和?ADE是等边三角形,BD与CE相交于点O
结论1:△ABD≌△ACE,BD=CE(左手拉左手等于右手拉右手)
结论2:∠BOC=60°
结论3:AO平分∠BOE
条件:?ABC和?ADE是等边三角形,BD与CE相交于点O
结论1:△ABD≌△ACE,BD=CE(左手拉左手等于右手拉右手)
结论2:∠BOC=60°
结论3:AO平分∠BOE
典例精讲:
[问题提出]
(1)如图false均为等边三角形,点false分别在边false上.将false绕点false沿顺时针方向旋转,连结false.在图false中证明false.
4650105103505
[学以致用]
(2)在false的条件下,当点false在同一条直线上时,false的大小为 度.
[拓展延伸]
(3)在false的条件下,连结false.若false直接写出false的面积false的取值范围.
【思路点拨】
(1)根据“手拉手”模型1,证明false即可;
(2)分“当点false在线段false上”和“当点false在线段false的延长线上”两种情况,再根据“手拉手”模型1中的结论2即可求得false的大小;
(3)分别求出false的面积最大值和最小值即可得到结论
【详解】
(1)false均为等边三角形,
false,false,
false,
即false
在false和false中
false
false;
(2)当false在同一条直线上时,分两种情况:
①当点false在线段false上时,如图,
∵false是等边三角形,
false,
false,
由(1)可知,false,
false,
false
②当点false在线段false的延长线上时,如图,
false是等边三角形,
false
false,
由(1)可知,false
false,
false false
综上所述,false的大小为false或false
(3)过点A作false于点F,当点D在线段AF上时,点D到BC的距离最短,此时,点D到BC的距离为线段DF的长,如图:
false是等边三角形,false,false
false,false
false
false
此时false;
当D在线段FA的延长线上时,点D到BC的距离最大,此时点D到BC的距离为线段DF的长,如图,
false是等边三角形,false,false
false,false,
false
false
false
此时,false;
综上所述,false的面积S 取值是false
【解题技法】 “手拉手”模型1中,对应边“拉手线”组成的两个三角形全等
实战演练:
1.(1)如图1,已知△CAB和△CDE均为等边三角形,D在AC上,E在CB上,易得线段AD和BE的数量关系是 .
(2)将图1中的△CDE绕点C旋转到图2的位置,直线AD和直线BE交于点F.
①判断线段AD和BE的数量关系,并证明你的结论;
②图2中∠AFB的度数是 .
(3)如图3,若△CAB和△CDE均为等腰直角三角形,∠ABC=∠DEC=90°,AB=BC,DE=EC,直线AD和直线BE交于点F,分别写出∠AFB的度数,线段AD、BE间的数量关系.
(二)有公共顶点的等腰直角三角形
26860572390条件:?ABC和?ADE是等腰直角三角形,BD与CE相交于点O
结论1:△ABD≌△ACE,BD=CE(左手拉左手等于右手拉右手)
结论2:∠BOC=90°
结论3: AO平分∠BOE
条件:?ABC和?ADE是等腰直角三角形,BD与CE相交于点O
结论1:△ABD≌△ACE,BD=CE(左手拉左手等于右手拉右手)
结论2:∠BOC=90°
结论3: AO平分∠BOE
8763071120
典例精讲:
如图,△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=α,AC、BD交于M
(1)如图1,当α=90°时,∠AMD的度数为 °
(2)如图2,当α=60°时,∠AMD的度数为 °
(3)如图3,当△OCD绕O点任意旋转时,∠AMD与α是否存在着确定的数量关系?如果存在,请你用表示∠AMD,并图3进行证明;若不确定,说明理由.
【思路点拨】
(1)如图1中,设OA交BD于K.根据“手拉手”模型2证明△BOD≌△AOC,推出∠OBD=∠OAC,由∠AKM=∠BKO,可得∠AMK=∠BOK=90°;
(2)如图2中,设OA交BD于K.根据“手拉手”模型1证明△BOD≌△AOC,推出∠OBD=∠OAC,由∠AKM=∠BKO,推出∠AMK=∠BOK=60°;
(3)如图3中,设OA交BD于K.根据“手拉手”模型3证明△BOD≌△AOC,根据“手拉手”模型中的结论2可得∠AMD=180°-α.
【详解】
(1)如图1中,设OA交BD于K.
∵OA=OB,OC=OD,∠AOB=∠COD=α,
∴∠BOD=∠AOC,∴△BOD≌△AOC,
∴∠OBD=∠OAC,
∵∠AKM=∠BKO,∴∠AMK=∠BOK=90°.
故答案为90.
(2)如图2中,设OA交BD于K.
∵OA=OB,OC=OD,∠AOB=∠COD=α,
∴∠BOD=∠AOC,
∴△BOD≌△AOC,∴∠OBD=∠OAC,
∵∠AKM=∠BKO,∴∠AMK=∠BOK=60°.
故答案为60.
(3)如图3中,设OA交BD于K.
∵OA=OB,OC=OD,∠AOB=∠COD=α,
∴∠BOD=∠AOC,∴△BOD≌△AOC,
∴∠OBD=∠OAC,
∵∠AKO=∠BKM,∴∠AOK=∠BMK=α.
∴∠AMD=180°﹣α.
【解题技法】“手拉手”模型2中,两条“拉手线”所在直线的夹角与初始图形中公共顶点对应的角相等或互补
实战演练:
1.已知:如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点E在BC边上.
(1)求证:△ACD≌△ABE;
(2)若∠CDE=60°,求∠AEB的度数.
2.△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°
(1)如图1,点D,E在AB,AC上,则BD,CE满足怎样的数量关系和位置关系?
(2)如图2,点D在△ABC内部,点E在△ABC外部,连结BD,CE,则BD,CE满足怎样的数量关系和位置关系?请说明理由.
(3)如图3,点D,E都在△ABC外部,连结BD,CE,CD,EB,BD与CE相交于F点.
①若BD=4,求四边形BCDE的面积.
②若AB=2,AD=1,设CD2=x,EB2=y,求y与x之间的函数关系式.
3. 如图乙,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)如图甲,将△ADE绕点A旋转,当C、D、E在同一条直线上时,连接BD、BE,则下列给出的四个结论中,其中正确的是哪几个 .(回答直接写序号)
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2)
(2)若AB=6,AD=3,把△ADE绕点A旋转:
①当∠CAE=90°时,求PB的长;
②直接写出旋转过程中线段PB长的最大值和最小值.
(三)顶角相等的等腰三角形
7810572390条件:?ABC和?ADE是等腰三角形,且∠BAC =∠DAE ,BD与CE相交于点O
结论1:△ABD≌△ACE,BD=CE(左手拉左手等于右手拉右手)
结论2:∠BOC=∠BAC
结论3: AO平分∠BOE
条件:?ABC和?ADE是等腰三角形,且∠BAC =∠DAE ,BD与CE相交于点O
结论1:△ABD≌△ACE,BD=CE(左手拉左手等于右手拉右手)
结论2:∠BOC=∠BAC
结论3: AO平分∠BOE
190572390
典例精讲:
观察猜想
如图1,有公共直角顶点false的两个不全等的等腰直角三角尺叠放在一起,点false在false上,点false在false上.
(1)在图1中,你发现线段false,false的数量关系是___________,直线false,false的位置关系是________.
操作发现
(2)将图1中的false绕点false逆时针旋转一个锐角得到图2,这时(1)中的两个结论是否成立?作出判断并说明理由;
拓广探索
(3)如图3,若只把“有公共直角顶点false的两个不全等的等腰直角三角尺”改为“有公共顶角为false(锐角)的两个不全等等腰三角形”,false绕点false逆时针旋转任意一个锐角,这时(1)中的两个结论仍然成立吗?作出判断,不必说明理由.
(1)false,false;(2)将图1中的false绕点false逆时针旋转一个锐角时,两个结论成立.理由见解析;(3)结论false成立;结论false不成立.
【思路点拨】
(1)根据△ABC和△ADE是等腰直角三角形,得到AB=AC,AD=AE,∠A=90°,即可得出结论;
(2)由旋转的性质得到∠DAB=∠EAC.根据“手拉手”模型2证明△ABD≌△ACE,得出BD=CE.再根据“手拉手”模型2的结论2可得出false.
(3)根据“手拉手”模型3证明△ABD≌△ACE,可得BD=CE成立,再根据“手拉手”模型3的结论2可得出BD⊥CE不成立.
【详解】
(1)∵△ABC和△ADE是等腰直角三角形,∴AB=AC,AD=AE,∠A=90°,∴BD=CE,BD⊥CE.
故答案为:BD=CE,BD⊥CE.
(2)将图1中的△ABC绕点A逆时针旋转一个锐角时,两个结论成立.理由如下:
由旋转得:∠DAB=∠EAC.
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS).
∴BD=CE.
如图,延长DB,交CE于点F,交AE于点O.
∵△ABD≌△ACE,
∴∠ADB=∠AEC.
∵∠AOD=∠EOF.
∴∠OFE=∠OAD.
∵∠OAD=90°,
∴∠DFE=90°,即BD⊥CE.
(3)结论BD=CE成立,结论BD⊥CE不成立.理由如下:
由旋转得:∠DAE=∠BAC,
∴∠DAB=∠EAC.
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS).
∴BD=CE.
延长DB交CE于M,BD与AE交于点N.
∵△ABD≌△ACE,∴∠MEA=∠BDA.
∵∠ENM=∠DNA,∴∠EMN=∠EAD.
∵∠EAD≠90°,∴∠EMN≠90°,∴BD⊥CE不成立.
【解题技法】对于以等腰三角形的顶点为旋转点,进行适当旋转的题目,连接对应点构造新的三角形,根据“手拉手”模型3证明三角形全等即可解决问题
实战演练:
1、如图,在false中,false,D、E分别是false、false的中点,false.
(1)如图12-1,若false,求false的长度(用含a的代数式表示);
(2)如图12-2,将false绕点A顺时针旋转,旋转角为false,连接false、false,判断false与false的数量关系,并说明理由;
(3)在(2)的条件下,当false的外心在三角形的外部时,请直接写出false的取值范围.
2、如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE,CF相交于点D,
(1)求证:BE=CF ;
(2)当四边形ACDE为菱形时,求BD的长.
(四)有公共顶点的正方形
-102870137985519051437005条件:正方形ABCD和正方形CEFG, BD与CE相交于点O
结论1:△BCE≌△DCE,BE=DG(左手拉左手等于右手拉右手)
结论2:∠BOG=90°
结论3: CO平分∠BOG
条件:正方形ABCD和正方形CEFG, BD与CE相交于点O
结论1:△BCE≌△DCE,BE=DG(左手拉左手等于右手拉右手)
结论2:∠BOG=90°
结论3: CO平分∠BOG
典例精讲:
规定:有一角重合,且角的两边叠合在一起的两个相似四边形叫做“嵌套四边形”,如图,四边形ABCD和AMPN就是嵌套四边形.
(1)问题联想
如图①,嵌套四边形ABCD,AMPN都是正方形,现把正方形AMPN以A为中心顺时针旋转150°得到正方形AM'P'N',连接BM',DN'交于点O,则BM'与DN'的数量关系为_____,位置关系为_____;
(2)类比探究
如图②,将(1)中的正方形换成菱形,∠BAD=∠MAN=60,其他条件不变,则(1)中的结论还成立吗? 若成立,请说明理由;若不成立,请给出正确的结论,并说明理由;
(3)拓展延伸
如图3,将(1)中的嵌套四边形ABCD和AMPN换成是长和宽之比为2:1的矩形,旋转角换成α(90°<α<180°),其他条件不变,请直接写出BM'与DN'的数量关系和位置关系.
【思路点拨】
(1)根据“手拉手”模型4证明△ABM’≌△AND’,得到false,再根据“手拉手”模型4的结论2得出false;
(2)根据“手拉手”模型4和菱形的性质证明false,再推false,故可求解;
(3)根据“手拉手”模型4和矩形的性质证明false,得到false,再推出false即可求解.
【详解】
(1)如图设false,false交于点H,,
∵四边形ABCD,AMPN都是正方形,把正方形AMPN以A为中心顺时针旋转150°得到正方形AM'P'N',
∴AB=AD,AM’=AD’, false
∴△ABM’≌△AND’,
∴false,∠ABM’=∠ADN’,
∵∠ADN’+∠DHA+∠DAH=180°,∠ABM’+∠BHO+∠BOD=180°,
又∠DHA=∠BHO
∴false,即false
故答案为:false,false;
(2)false成立,false不成立,false与false相交,且夹角为false.
理由:设false,false交于点false,
由旋转的性质可得false.
∵四边形false,false都是菱形,
∴false,false,
∴false,
∴false,false.
又∵false,
∴false;
故false与false相交,且夹角为false;
(3)false,false,理由如下:
设false,false交于点false,
由旋转的性质可得false.
∵四边形ABCD和AMPN是长和宽之比为2:1的矩形
∴false,false,
∴false
∴false,
∴false,false.
又∵false,
∴false
∴false,false.
【解题技法】利用“手拉手”模型4证明三角形全等,再把特殊情况推广到一般情况,再运用类比的思想方法是一种常用的数学方法.
实战演练:
(1)在正方形ABCD中,G是CD边上的一个动点(不与C、D重合),以CG为边在正方形ABCD外作一个正方形CEFG,连结BG、DE,如图①.直接写出线段BG、DE的关系 ;
(2)将图①中的正方形CEFG绕点C按顺时针方向旋转任意角度false,如图②,试判断(1)中的结论是否成立?若成立,直接写出结论,若不成立,说明理由;
(3)将(1)中的正方形都改为矩形,如图③,再将矩形CEFG绕点C按顺时针方向旋转任意角度false,如图④,若AB=a,BC=b;CE =ka,CG=kb,(false)试判断(1)中的结论是否仍然成立?并说明理由.
(五)有公共顶点的直角三角形
190533020条件:CD//AB,且∠AOB =∠COD=90° ,BD与CA相交于点E
结论1:△AOC~△BOD
结论2: false
结论3: 四边形ABCD的面积=12AC.BD
条件:CD//AB,且∠AOB =∠COD=90° ,BD与CA相交于点E
结论1:△AOC~△BOD
结论2: false
结论3: 四边形ABCD的面积=12AC.BD
-13144536195
典例精讲:
1.(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①false的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断false的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=false,请直接写出当点C与点M重合时AC的长.
【思路点拨】
(1)①根据“手拉手”模型3证明△COA≌△DOB,得AC=BD;
②根据“手拉手”模型3的结论2得出∠AMB=∠AOB;
(2)根据“手拉手”模型5证明△AOC∽△BOD,则false,再根据“手拉手”模型5的结论2得出∠AMB的度数;
(3)正确画图形,当点C与点M重合时,有两种情况,如图3和4,根据在旋转过程中,始终有 “手拉线”AC与BD垂直,据此设出未知数,运用勾股定理求解即可.
【详解】
(1)问题发现:
①如图1,
∵∠AOB=∠COD=40°,∴∠COA=∠DOB,
∵OC=OD,OA=OB,∴△COA≌△DOB(SAS),
∴AC=BD,∴false
②∵△COA≌△DOB,∴∠CAO=∠DBO,
∵∠AOB=40°,∴∠OAB+∠ABO=140°,
在△AMB中,∠AMB=180°-(∠CAO+∠OAB+∠ABD)=180°-(∠DBO+∠OAB+∠ABD)=180°-140°=40°,
(2)类比探究:
如图2,false,∠AMB=90°,理由是:
Rt△COD中,∠DCO=30°,∠DOC=90°,
∴false,
同理得:false,
∴false, ∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD,∴△AOC∽△BOD,
∴false ,∠CAO=∠DBO,
在△AMB中,∠AMB=180°-(∠MAB+∠ABM)=180°-(∠OAB+∠ABM+∠DBO)=90°;
(3)拓展延伸:
①点C与点M重合时,如图3,
同理得:△AOC∽△BOD,∴∠AMB=90°,false,
设BD=x,则AC=falsex,
Rt△COD中,∠OCD=30°,OD=1,
∴CD=2,BC=x-2,
Rt△AOB中,∠OAB=30°,OB=false,
∴AB=2OB=2false,
在Rt△AMB中,由勾股定理得:AC2+BC2=AB2,
(falsex)2+(x?2)2=(2false)2,
x2-x-6=0,
(x-3)(x+2)=0,
x1=3,x2=-2,
∴AC=3false;
②点C与点M重合时,如图4,
同理得:∠AMB=90°,false,
设BD=x,则AC=falsex,
在Rt△AMB中,由勾股定理得:AC2+BC2=AB2,
(falsex)2+(x+2)2=(2false)2.
x2+x-6=0,
(x+3)(x-2)=0,
x1=-3,x2=2,
∴AC=2false;.
综上所述,AC的长为3false或2false.
【解题技法】用运动和变化的眼光观察和研究图形,把握图形旋转过程中的等量关系,抓住利用“手拉手”模型5得出△AOC∽△BOD是解题的关键.
实战演练:
1、如图1,在Rt△ABC中,∠B=90°,AB=4,BC=2,点D、E分别是边BC、AC的中点,连接DE.将△CDE绕点C逆时针方向旋转,记旋转角为α.
(1)问题发现
①当α=0°时,false=_______;
②当α=180°时,false=______.
(2)拓展探究
试判断:当0°≤α<360°时,false的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
△CDE绕点C逆时针旋转至A、B、E三点在同一条直线上时,求线段BD的长.
2、如图(1),在false中,false,点false分别是边false的中点,连接false.
(1)如图①,求false的值;
(2)将false绕点false顺时针旋转到如图(2)的位置时,false的大小是否发生变化,若不变化,请说明理由;若发生变化,请求出它的值;
(3)将false绕点false顺时针旋转到直线false的下方,且false在同一直线上时,如图(3),求线段false的长.
(六)有公共顶点的任意三角形
306705296545条件:CD//AB,BD与CA相交于点E
结论1:△AOC~△BOD
结论2: ∠AEB =∠COD=∠AOB
结论3: 点E在△BOA的外接圆上
条件:CD//AB,BD与CA相交于点E
结论1:△AOC~△BOD
结论2: ∠AEB =∠COD=∠AOB
结论3: 点E在△BOA的外接圆上
154305-52705
典例精讲:
在false,false,false.点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.
(1)观察猜想
如图1,当false时,false的值是 ,直线BD与直线CP相交所成的较小角的度数是 .
(2)类比探究
如图2,当false时,请写出false的值及直线BD与直线CP相交所成的小角的度数,并就图2的情形说明理由.
(3)解决问题
当false时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时false的值.
【思路点拨】
(1)如图1中,延长CP交BD的延长线于E,设AB交EC于点O.根据“手拉手”模型1证明false,得出CP=BD,.根据“手拉手”模型1的结论2即可解决问题.
(2)如图2中,设BD交AC于点O,BD交PC于点E.根据“手拉手”模型6证明false,得出false即可解决问题.
(3)分两种情形:①如图3﹣1中,当点D在线段PC上时,延长AD交BC的延长线于H.证明false即可解决问题.
②如图3﹣2中,当点P在线段CD上时,同法可证:false解决问题.
【详解】
解:(1)如图1中,延长CP交BD的延长线于E,设AB交EC于点O.
false,
false,
false,false,
false,
false,false,
false,
false,
false,线BD与直线CP相交所成的较小角的度数是false,
故答案为1,false.
(2)如图2中,设BD交AC于点O,BD交PC于点E.
false,
false,
false,
false,
false,false,
false,
false,
false直线BD与直线CP相交所成的小角的度数为false.
(3)如图3﹣1中,当点D在线段PC上时,延长AD交BC的延长线于H.
false,false,
false,
false,
false,
false,
false,
false,
false,false,
false,
false,
false,
false,
false,
false,
false,
false,
false,
falseA,D,C,B四点共圆,
false,false,
false,
false,设false,则false,false,
falsec.
如图3﹣2中,当点P在线段CD上时,同法可证:false,设false,则false,false,
false,
false.
【解题技法】“手拉手”模型中,对应边和“拉手线”组成的两个三角形相似,学会根据题干的条件灵活运用,运用分类讨论的数学思想思考问题.
实战演练:
在false中,false,false是平面内不与点false重合的任意一点,连接false,将线段false绕点false顺时针旋转false得到线段false,连接false是false的中点,false是false的中点.
(1)问题发现:
如图1,当false时,false的值是_________,直线false与直线false相交所成的较小角的度数是________.
(2)类比探究:
如图2,当false时,请写出false的值及直线false与直线false相交所成的较小角的度数,并说明理由.
(3)解决问题:
如图3,当false时,若false是false的中点,点false在直线false上,且点false在同一条直线上,请直接写出false的值.
同课章节目录
