【备战2021年中考数学几何模型汇编专练】专题五 半角模型 复习教案
文档属性
| 名称 | 【备战2021年中考数学几何模型汇编专练】专题五 半角模型 复习教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-30 10:17:22 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
数学模型-----半角模型
几何是初中数学中非常重要的内容_?????¨??°?????????_习过程中,若能抓住基本图形,举一反三,定能引领学生领略到“一图一世界”的风采。下面先给大家介绍一种常见的数学模型---半角模型,通过对模型的理解和掌握,把模型的结论融会贯通,理解透彻,有助于理清思路、节省大量时间,遇到这一类题型,都是可以迎刃而解的。21世纪21世纪教育网有21世纪教育网21-cn-jy.com21*cnjy*com21世纪教育网版权所有
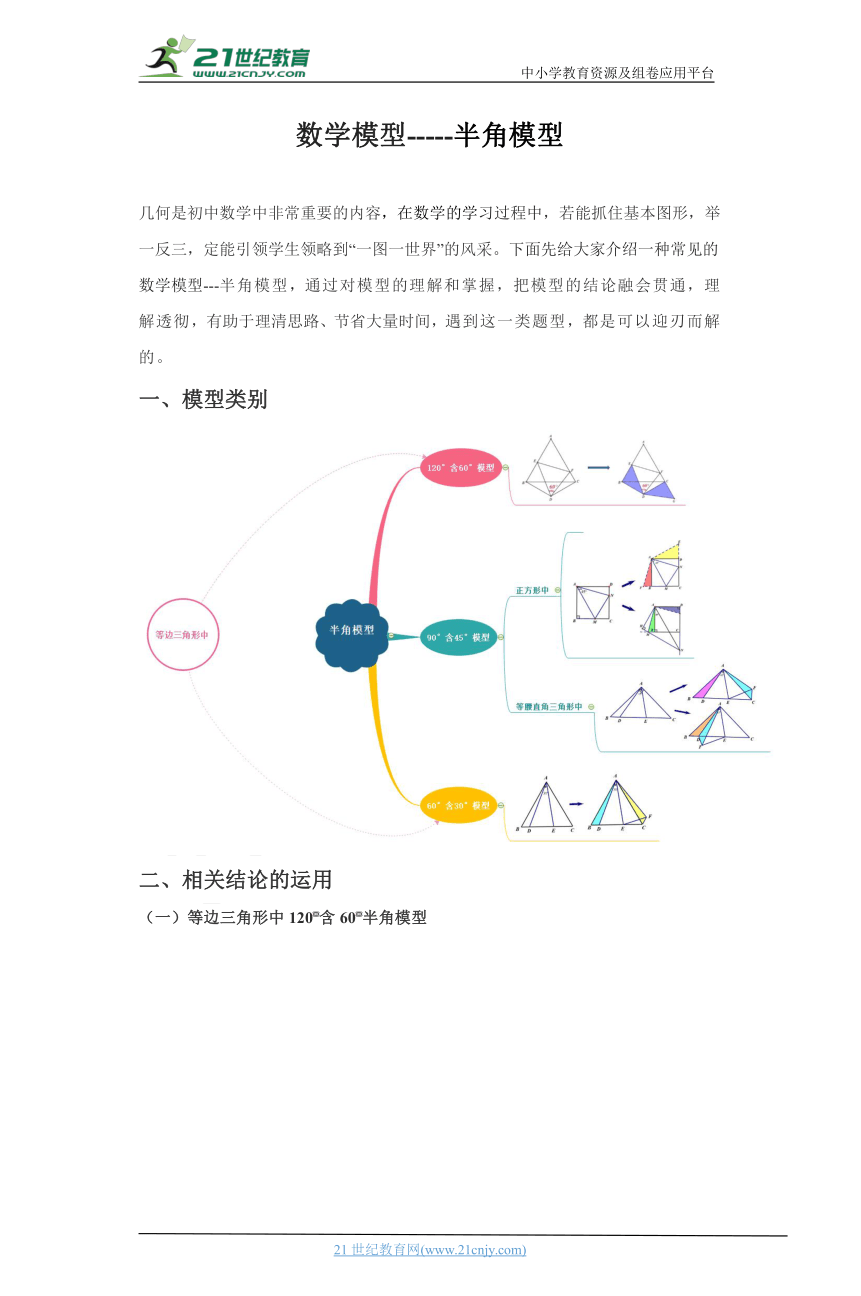
一、模型类别
二、相关结论的运用
(一)等边三角形中120含60半角模型
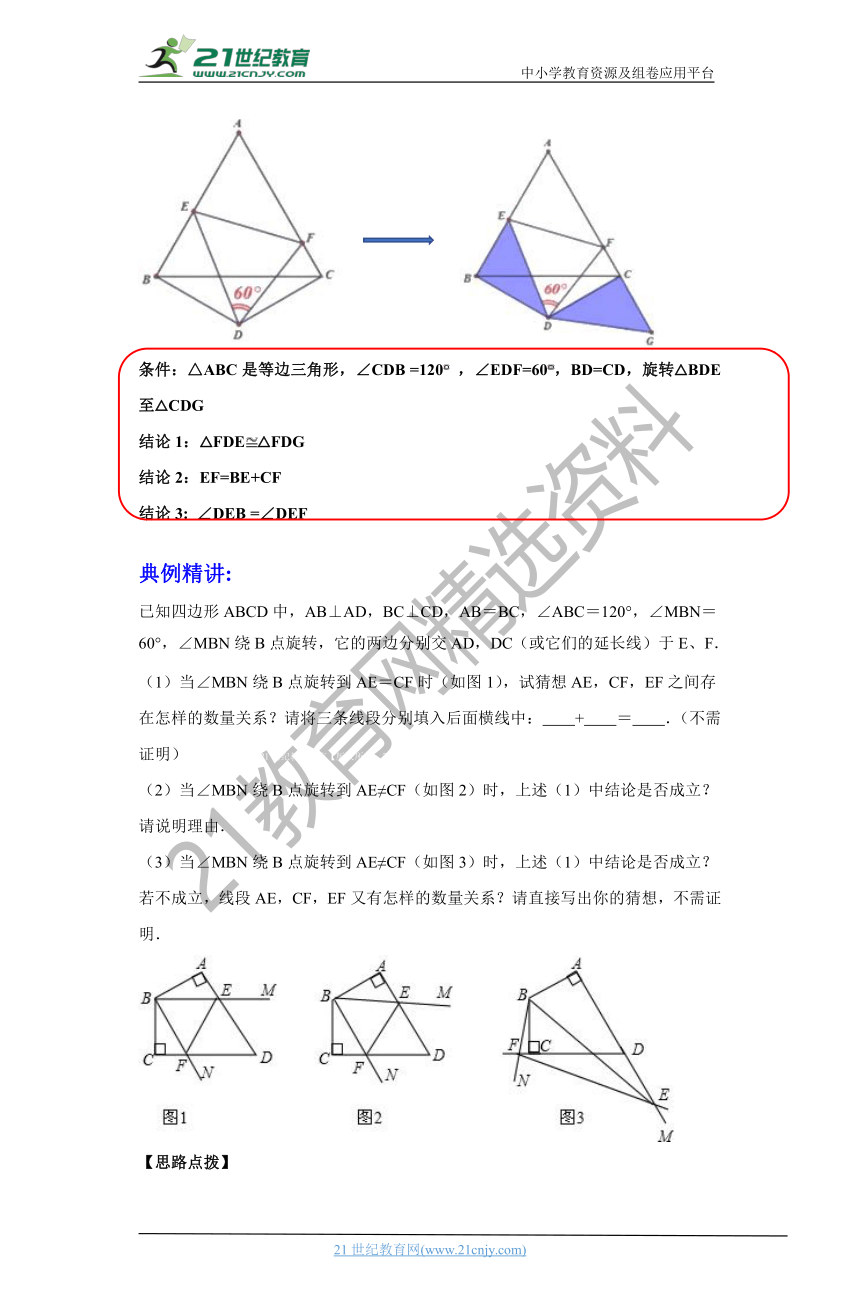
条件:△ABC是等边三角形,∠CDB =120 ,∠EDF=60,BD=CD,旋转△BDE至△CDG【来源:21·世纪·教育·网】www-2-1-cnjy-com21·cn·jy·com21·cn·jy·com
结论1:△FDE△FDG
结论2:EF=BE+CF
结论3: ∠DEB =∠DEF
典例精讲:
已知四边形ABCD中,AB⊥A_D???BC???C_D,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN绕B点旋转,它的两边分别交AD,DC(或它们的延长线)于E、F.
(1)当∠MBN绕B_??????è????°AE_=CF时(如图1),试猜想AE,CF,EF之间存在怎样的数量关系?请将三条线段分别填入后面横线中: + = .(不需证明)2-1-c-n-j-y21世纪21世纪教育网有【版权所有:21教育】2-1-c-n-j-y
(2)当∠MBN绕B点旋转到AE≠CF(如图2)时,上述(1)中结论是否成立?请说明理由.
(3)当∠MBN绕B点旋转到A_E???CF??????_图3)时,上述(1)中结论是否成立?若不成立,线段AE,CF,EF又有怎样的数量关系?请直接写出你的猜想,不需证明.21*cnjy*com【来源:21cnj*y.co*m】【出处:21教育名师】
【思路点拨】
(1)证明△ABE≌△CBF且△BEF是等边三角形即可;
(2)根据“半角”模型1,先_è?????BAE???_△BCG,再根据“半角”模型1中的结论2得出△GBF≌△EBF,再根据“半角”模型1中的结论3即可;
(3)根据“半角”模型1,先证△BAH≌△BCF,再根据“手拉手”模型1中的结论2得出△EBF≌△EBH即可.
【详解】
解:(1)如图1,
在△ABE和△CBF中,
,
∴△ABE≌△CBF(SAS),
∴∠CBF=∠EBA,BE=BF,
∵∠ABC=120°,∠EBF=60°,
∴△BEF是等边三角形,CF=,AE=,
∴EF=BE=BF=AE+CF;
(2)如图2,延长FC至G,使AE=CG,连接BG,
在△BAE和△BCG中,
,
∴△BAE≌△BCG(SAS),
∴∠ABE=∠CBG,BE=BG,
∵∠ABC=120°,∠EBF=60°,
∴∠ABE+∠CBF=60°,
∴∠CBG+∠CBF=60°,
∴∠GBF=∠EBF,
在△GBF和△EBF中,
,
∴△GBF≌△EBF(SAS),
∴EF=GF=CF+CG=CF+AE;
(3)不成立,但满足新的数量关系.
如图3,在AE上截取AH=CF,连接BH,
在△BAH和△BCF中,
,
∴△BAH≌△BCF(SAS),
∴BH=BF,∠ABH=∠CBF,
∵∠EBF=60°=∠FBC+∠CBE
∴∠ABH+∠CBE=60°,
∵∠ABC=120°,
∴∠HBE=60°=∠EBF,
在△EBF和△HBE中,
,
∴△EBF≌△EBH(SAS),
∴EF=EH,
∴AE=EH+AE=EF+CF.
【解题技法】本题典型的利用“半角”模型1,其基本思路是“旋转补短”,从而构造全等三角形.
实战演练:
1、如图1,在菱形ABCD中,AC=2,BD=2,AC,BD相交于点O.
(1)求边AB的长;
(2)求∠BAC的度数;
(3)如图2,将一个足够大_??????è§????è§????_60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF.判断△AEF是哪一种特殊三角形,并说明理由.2·1·c·n·j·y21cnjy.com
2、在平行四边形ABCD中_??????E???F???_别在边AD,AB上(均不与顶点重合),且∠BCD=120°,∠ECF=60°.【出处:21教育名师】21世纪教育网21-cn-jy.com
(1)如图1,若AB=AD,求证:△AEC≌△BFC;
(2)如图2,若AB=2AD,过点C作CM⊥AB于点M,求证:①AC⊥BC;②AE=2FM;
(3)如图3,若AB=3AD,试探究线段CE与线段CF的数量关系.
(二)等腰直角三角形中90含45半角模型
条件:△ABC是等腰直角三角形,∠CAB =90 ,AB=AC,∠DAE=45,旋转△BDE至△CDG(△BDE沿AD翻折到△ADF)2·1·c·n·j·y
结论1:△ADE△AFE(△ACE△AFE)
结论2: DE2=BD2+EC2
结论3:C?CEF=BC(C?DEF=BC)
典例精讲:
已知Rt△ABC中,∠ACB=_90?°???CA_=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(1)当扇形CEF绕点C在∠ACB的内部旋转时,如图①,求证:MN2=AM2+BN2;
思路点拨:考虑MN_2???AM2+_BN2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.【来源:21cnj*y.co*m】2·1·c·n·j·y
请你完成证明过程:
(2)当扇形CE_F??????C???è??_至图②的位置时,关系式MN2=AM2+BN2是否仍然成立?若成立,请证明;若不成立,请说明理由.21世纪21世纪教育网有
【思路点拨】
(1)将△AC_M?????????CE_对折,得△DCM,连DN,根据“半角”模型2,证明出△CDN≌△CBN,再根据“半角”模型2的结论2即可;【出处:21教育名师】
(2)将△ACM沿直_???CE?????????_得△GCM,连GN,根据“半角”模型2,证明△CGN≌△CBN,再根据“半角”模型2的结论2即可;21世纪教育网21-cn-jy.com
【详解】
(1)证明:
将△ACM沿直线CE对折,得△DCM,连DN,
则△DCM≌△ACM.
有CD=CA,DM=AM,∠DCM=∠ACM,∠CDM=∠A.
又由CA=CB,得 CD=CB.
由∠DCN=∠ECF﹣∠DCM=45°﹣∠DCM,
∠BCN=∠ACB﹣∠ECF﹣∠ACM=90°﹣45°﹣∠ACM,
得∠DCN=∠BCN.
又CN=CN,
∴△CDN≌△CBN.
∴DN=BN,∠CDN=∠B.
∴∠MDN=∠CDM+∠CDN=∠A+∠B=90°.
∴在Rt△MDN中,由勾股定理,
得MN2=DM2+DN2.即MN2=AM2+BN2.
(2)关系式MN2=AM2+BN2仍然成立.
证明:将△ACM沿直线CE对折,得△GCM,连GN,
则△GCM≌△ACM.
有CG=CA,GM=AM,
∠GCM=∠ACM,∠CGM=∠CAM.
又由CA=CB,得 CG=CB.
由∠GCN=∠GCM+∠ECF=∠GCM+45°,
∠BCN=∠ACB﹣∠ACN=90°﹣(∠ECF﹣∠ACM)=45°+∠ACM.
得∠GCN=∠BCN.
又CN=CN,
∴△CGN≌△CBN.
有GN=BN,∠CGN=∠B=45°,∠CGM=∠CAM=180°﹣∠CAB=135°,
∴∠MGN=∠CGM﹣∠CGN=135°﹣45°=90°.
∴在Rt△MGN中,由勾股定理,
得MN2=GM2+GN2.即MN2=AM2+BN2.
【解题技法】利用“半角”模型2,正确作出辅助线,构造直角三角形是解题的关键。
实战演练:
在等腰△ABC中,CA=CB,点D,E在射线AB上,不与A,B重合(D在E的左边),且∠DCE=∠ACB.21*cnjy*com21教育网21教育名师原创作品【来源:21cnj*y.co*m】
(1)如图1,若∠ACB=90°,将△CAD沿CD翻折,点A与M重合,求证:△MCE≌△BCE;
(2)如图2,若∠ACB=120°,且以AD、DE、EB为边的三角形是直角三角形,求的值;
(3)∠ACB=120°,点D在射线AB上运动,AC=3,则AD的取值范围为 .
(三)正方形中90含45半角模型
条件:正方形ABCD中,∠MAN =45 ,旋转△ABF至△AND;
结论1:△AFM△AMN
结论2: MN=BM+DN(MN=DN-BM)
结论3:C?MCN=2AB;
结论4: ()
典例精讲:
(1)(发现证明)
如图1,在正方形ABCD中,点E_???F?????????B_C,CD边上的动点,且∠EAF=45°,求证:EF=DF+BE.21·世纪*教育网2-1-c-n-j-y21*cnjy*com21教育网
小明发现,当把△ABE_??????Aé?????é??_旋转90°至△ADG,使AB与AD重合时能够证明,请你给出证明过程.www-2-1-cnjy-com21cnjy.com【版权所有:21教育】
(2)(类比引申)①_??????2?????¨???_方形ABCD中,如果点E,F分别是CB,DC延长线上的动点,且∠EAF=45°,则(1)中的结论还成立吗?请写出证明过程.
②如图3,如果点E,F分别是BC_???CD???é?????_上的动点,且∠EAF=45°,则EF,BE,DF之间的数量关系是 (不要求证明)21教育名师原创作品
(3)(联想拓展)如图1,若正方形ABCD的边长为6,AE=3,求AF的长.
【思路点拨】
(1)(发现证明)根据“半角”模型3,证明出△EAF≌△GAF,再根据“半角”模型3的结论2即可得证;21教育名师原创作品
(2)(类比引申)①根据“半角”模型3,证明出△EAF≌△GAF,再根据“半角”模型3的结论2即可得证;21*cnjy*com
②根据“半角”模型3,证明△AFE≌△ANE,再根据“半角”模型3的结论2即可得证;
(3)(联想拓展)
求出DG=2,设DF=x,则根据_??????è§?????¨????_3的结论2得出EF=DG=x+3,CF=6﹣x,在Rt△EFC中,得出关于x的方程,解出x则可得解.
【详解】
(1)(发现证明)
证明:把△ABE绕点A顺时针旋转90°至△ADG,如图1,
∴∠BAE=∠DAG,AE=AG,
∵∠EAF=45°,
∴∠BAE+∠FAD=45°,
∴∠DAG+∠FAD=45°,
∴∠EAF=∠FAG,
∵AF=AF,
∴△EAF≌△GAF(SAS),
∴EF=FG=DF+DG,
∴EF=DF+BE;
(2)(类比引申)
①不成立,结论:EF=DF﹣BE;
证明:如图2,将△ABE绕点A顺时针旋转90°至△ADM,
∴∠EAB=∠MAD,AE=AM,∠EAM=90°,BE=DM,
∴∠FAM=45°=∠EAF,
∵AF=AF,
∴△EAF≌△MAF(SAS),
∴EF=FM=DF﹣DM=DF﹣BE;
②如图3,将△ADF绕点A逆时针旋转90°至△ABN,
∴AN=AF,∠NAF=90°,
∵∠EAF=45°,
∴∠NAE=45°,
∴∠NAE=∠FAE,
∵AE=AE,
∴△AFE≌△ANE(SAS),
∴EF=EN,
∴BE=BN+NE=DF+EF.
即BE=EF+DF.
故答案为:BE=EF+DF.
(3)(联想拓展)
解:由(1)可知AE=AG=3,
∵正方形ABCD的边长为6,
∴DC=BC=AD=6,
∴==3.
∴BE=DG=3,
∴CE=BC﹣BE=6﹣3=3,
设DF=x,则EF=DG=x+3,CF=6﹣x,
在Rt△EFC中,∵CF2+CE2=EF2,
∴(6﹣x)2+32=(x+3)2,
解得:x=2.
∴DF=2,
∴AF===2.
【解题技法】“半角”模型3,常与旋转的性质、全等三角形的判定与性质以及勾股定理的综合应用,将分散的条件集中起来,将隐秘的关系显现出来.
实战演练:
1、思维探索:
在正方形ABCD中,AB=4,∠EAF的两边分别交射线CB,DC于点E,F,∠EAF=45°.
(1)如图1,当点E,F分别在线段BC,CD上时,△CEF的周长是 8 ;
(2)如图2,当点E,F分别在CB,DC的延长线上,CF=2时,求△CEF的周长;
拓展提升:如图3,在R_t???ABC???_,∠ACB=90°,CA=CB,过点B作BD⊥BC,连接AD,在BC的延长线上取一点E,使∠EDA=30°,连接AE,当BD=2,∠EAD=45°时,请直接写出线段CE的长度.21cnjy.com21·cn·jy·com21·世纪*教育网
2、(1)如图,在正_??????_ABC_D 中,∠FAG=45°,请直接写出 DG,BF 与FG 的数量关系,不需要证明.21·cn·jy·com【来源:21·世纪·教育·网】2-1-c-n-j-y21cnjy.com
(2)如图,在__Rt???AB_C 中,∠BAC=90°,AB=AC,E,F 分别是 BC 上两点,∠EAF=45°,【出处:21教育名师】21*cnjy*comwww.21-cn-jy.com
①写出 BE,CF,EF 之间的数量关系,并证明.
②若将(2)中的△AE_F_??????_A_ 旋转至如图所示的位置,上述结论是否仍然成立? 若不成立,直接写出新的结论 ,无需证明.【版权所有:21教育】【来源:21·世纪·教育·网】
(3)如图,△AEF 中∠EAF=45°,AG⊥EF 于 G,且GF=2,GE=3,则 = .
(四)等边三角形中60含30半角模型
条件:△ABC是等边三角形,∠DAE =30 ,旋转△ABD至△ACF;
结论1:△ADE△AFE
结论2:∠ECF =120
结论3:C?ECF=AB;
典例精讲:
转前后的线段之间、角之间的关系进行了探究.
(一)尝试探究
如图1所示,在四边形ABCD中,_AB???AD???_∠BAD=60°,∠ABC=∠ADC=90°,点E、F分别在线段BC、CD上,∠EAF=30°,连接EF.【来源:21cnj*y.co*m】
(1)如图2所示,将△ABE绕点_Aé?????é?????è??_60°后得到△A′B′E′(A′B′与AD重合),请直接写出∠E′AF= 度,线段BE、EF、FD之间的数量关系为 .
(2)如图3,当点E、F分别在线_???BC???CD_的延长线上时,其他条件不变,请探究线段BE、EF、FD之间的数量关系,并说明理由.21教育名师原创作品
(二)拓展延伸
如图4,在等边△ABC中,E_???F???è??BC_上的两点,∠EAF=30°,BE=1,将△ABE绕点A逆时针旋转60°得到△A′B′E′(A′B′与AC重合),连接EE′,AF与EE′交于点N,过点A作AM⊥BC于点M,连接MN,求线段MN的长度.
【思路点拨】
(一)(1)(发现证明)根据“半角”模型4,证明出△AEF≌△AE′F,进而根据线段的和差关系得出结论;【来源:21·世纪·教育·网】
(2)先在BE上截取BG=DF,连接AG,根据“半角”模型4,判定△GAE≌△FAE,根据线段的和差关系得出结论;www-2-1-cnjy-com
(二)先根据“半角”模型4,判定△AEE′是等边三角形,进而得到和∠BAE=∠MAN,最后判定△BAE∽△MAN,并根据相似三角形对应边成比例,列出比例式求得MN的长.【版权所有:21教育】
解:(一)(1)将△ABE绕点A逆时针旋转60°后得到△A′B′E′,
则∠BAE=∠DAE',BE=DE′,AE=AE′,
∵∠BAD=60°,∠EAF=30°,
∴∠BAE+∠DAF=30°,
∴∠DAE'+∠DAF=30°,即∠FAE′=30°
∴∠EAF=∠FAE′,
在△AEF和△AE′F中,,
∴△AEF≌△AE′F(SAS),
∴EF=E′F,即EF=DF+DE′,
∴EF=DF+BE,即线段BE、EF、FD之间的数量关系为BE+DF=EF,
故答案为:30,BE+DF=EF;
(2)如图3,在BE上截取BG=DF,连接AG,
在△ABG和△ADF中,,
∴△ABG≌△ADF(SAS),
∴∠BAG=∠DAF,且AG=AF,
∵∠DAF+∠DAE=30°,
∴∠BAG+∠DAE=30°,
∵∠BAD=60°,
∴∠GAE=60°﹣30°=30°,
∴∠GAE=∠FAE,
在△GAE和△FAE中,,
∴△GAE≌△FAE(SAS),
∴GE=FE,
又∵BE﹣BG=GE,BG=DF,
∴BE﹣DF=EF,
即线段BE、EF、FD之间的数量关系为BE﹣DF=EF;
(二)如图4,将△ABE绕点A逆时针旋转60°得到△A′B′E′,则
AE=AE′,∠EAE′=60°,
∴△AEE′是等边三角形,
又∵∠EAF=30°,
∴AN平分∠EAE',
∴AN⊥EE′,
∴RtANE中,,
∵在等边△ABC中,AM⊥BC,
∴∠BAM=30°,
∴,且∠BAE+∠EAM=30°,
∴,
又∵∠MAN+∠EAM=30°,
∴∠BAE=∠MAN,
∴△BAE∽△MAN,
∴,即,
∴MN=.
【解题技法】根据“半角”模型,对图形进行分解、组合,抓住图形旋转前后的对应边相等,一般解题方法为作辅助线构造全等三角形或相似三角形.
实战演练:
(1)问题背景:
如图1:在四边形ABCD中,AB_???AD??????B_AD=120°,∠B=∠ADC=90°,E、F分别是BC,CD上的点且∠EAF=60°,探究图中线段BE、EF、FD之间的数量关系.21教育网21·世纪*教育网21教育网21·世纪*教育网
小王同学探究此问题的方法是,延_é??FD??°???G_.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;2·1·c·n·j·y21*cnjy*comwww-2-1-cnjy-com21*cnjy*com
(2)探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论 仍然成立(填“是”或“否”);
结论应用:
如图3,在某次_??????????????????_舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以45海里/小时的速度前进,同时舰艇乙沿北偏东50°的方向以60海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两地分别到达E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
能力提高:
如图4,等腰直角三角形ABC中,_???BAC???9_0°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为 .
_21?????????è?????(www.21cnjy.com)_
数学模型-----半角模型
几何是初中数学中非常重要的内容_?????¨??°?????????_习过程中,若能抓住基本图形,举一反三,定能引领学生领略到“一图一世界”的风采。下面先给大家介绍一种常见的数学模型---半角模型,通过对模型的理解和掌握,把模型的结论融会贯通,理解透彻,有助于理清思路、节省大量时间,遇到这一类题型,都是可以迎刃而解的。21世纪21世纪教育网有21世纪教育网21-cn-jy.com21*cnjy*com21世纪教育网版权所有
一、模型类别
二、相关结论的运用
(一)等边三角形中120含60半角模型
条件:△ABC是等边三角形,∠CDB =120 ,∠EDF=60,BD=CD,旋转△BDE至△CDG【来源:21·世纪·教育·网】www-2-1-cnjy-com21·cn·jy·com21·cn·jy·com
结论1:△FDE△FDG
结论2:EF=BE+CF
结论3: ∠DEB =∠DEF
典例精讲:
已知四边形ABCD中,AB⊥A_D???BC???C_D,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN绕B点旋转,它的两边分别交AD,DC(或它们的延长线)于E、F.
(1)当∠MBN绕B_??????è????°AE_=CF时(如图1),试猜想AE,CF,EF之间存在怎样的数量关系?请将三条线段分别填入后面横线中: + = .(不需证明)2-1-c-n-j-y21世纪21世纪教育网有【版权所有:21教育】2-1-c-n-j-y
(2)当∠MBN绕B点旋转到AE≠CF(如图2)时,上述(1)中结论是否成立?请说明理由.
(3)当∠MBN绕B点旋转到A_E???CF??????_图3)时,上述(1)中结论是否成立?若不成立,线段AE,CF,EF又有怎样的数量关系?请直接写出你的猜想,不需证明.21*cnjy*com【来源:21cnj*y.co*m】【出处:21教育名师】
【思路点拨】
(1)证明△ABE≌△CBF且△BEF是等边三角形即可;
(2)根据“半角”模型1,先_è?????BAE???_△BCG,再根据“半角”模型1中的结论2得出△GBF≌△EBF,再根据“半角”模型1中的结论3即可;
(3)根据“半角”模型1,先证△BAH≌△BCF,再根据“手拉手”模型1中的结论2得出△EBF≌△EBH即可.
【详解】
解:(1)如图1,
在△ABE和△CBF中,
,
∴△ABE≌△CBF(SAS),
∴∠CBF=∠EBA,BE=BF,
∵∠ABC=120°,∠EBF=60°,
∴△BEF是等边三角形,CF=,AE=,
∴EF=BE=BF=AE+CF;
(2)如图2,延长FC至G,使AE=CG,连接BG,
在△BAE和△BCG中,
,
∴△BAE≌△BCG(SAS),
∴∠ABE=∠CBG,BE=BG,
∵∠ABC=120°,∠EBF=60°,
∴∠ABE+∠CBF=60°,
∴∠CBG+∠CBF=60°,
∴∠GBF=∠EBF,
在△GBF和△EBF中,
,
∴△GBF≌△EBF(SAS),
∴EF=GF=CF+CG=CF+AE;
(3)不成立,但满足新的数量关系.
如图3,在AE上截取AH=CF,连接BH,
在△BAH和△BCF中,
,
∴△BAH≌△BCF(SAS),
∴BH=BF,∠ABH=∠CBF,
∵∠EBF=60°=∠FBC+∠CBE
∴∠ABH+∠CBE=60°,
∵∠ABC=120°,
∴∠HBE=60°=∠EBF,
在△EBF和△HBE中,
,
∴△EBF≌△EBH(SAS),
∴EF=EH,
∴AE=EH+AE=EF+CF.
【解题技法】本题典型的利用“半角”模型1,其基本思路是“旋转补短”,从而构造全等三角形.
实战演练:
1、如图1,在菱形ABCD中,AC=2,BD=2,AC,BD相交于点O.
(1)求边AB的长;
(2)求∠BAC的度数;
(3)如图2,将一个足够大_??????è§????è§????_60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF.判断△AEF是哪一种特殊三角形,并说明理由.2·1·c·n·j·y21cnjy.com
2、在平行四边形ABCD中_??????E???F???_别在边AD,AB上(均不与顶点重合),且∠BCD=120°,∠ECF=60°.【出处:21教育名师】21世纪教育网21-cn-jy.com
(1)如图1,若AB=AD,求证:△AEC≌△BFC;
(2)如图2,若AB=2AD,过点C作CM⊥AB于点M,求证:①AC⊥BC;②AE=2FM;
(3)如图3,若AB=3AD,试探究线段CE与线段CF的数量关系.
(二)等腰直角三角形中90含45半角模型
条件:△ABC是等腰直角三角形,∠CAB =90 ,AB=AC,∠DAE=45,旋转△BDE至△CDG(△BDE沿AD翻折到△ADF)2·1·c·n·j·y
结论1:△ADE△AFE(△ACE△AFE)
结论2: DE2=BD2+EC2
结论3:C?CEF=BC(C?DEF=BC)
典例精讲:
已知Rt△ABC中,∠ACB=_90?°???CA_=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(1)当扇形CEF绕点C在∠ACB的内部旋转时,如图①,求证:MN2=AM2+BN2;
思路点拨:考虑MN_2???AM2+_BN2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.【来源:21cnj*y.co*m】2·1·c·n·j·y
请你完成证明过程:
(2)当扇形CE_F??????C???è??_至图②的位置时,关系式MN2=AM2+BN2是否仍然成立?若成立,请证明;若不成立,请说明理由.21世纪21世纪教育网有
【思路点拨】
(1)将△AC_M?????????CE_对折,得△DCM,连DN,根据“半角”模型2,证明出△CDN≌△CBN,再根据“半角”模型2的结论2即可;【出处:21教育名师】
(2)将△ACM沿直_???CE?????????_得△GCM,连GN,根据“半角”模型2,证明△CGN≌△CBN,再根据“半角”模型2的结论2即可;21世纪教育网21-cn-jy.com
【详解】
(1)证明:
将△ACM沿直线CE对折,得△DCM,连DN,
则△DCM≌△ACM.
有CD=CA,DM=AM,∠DCM=∠ACM,∠CDM=∠A.
又由CA=CB,得 CD=CB.
由∠DCN=∠ECF﹣∠DCM=45°﹣∠DCM,
∠BCN=∠ACB﹣∠ECF﹣∠ACM=90°﹣45°﹣∠ACM,
得∠DCN=∠BCN.
又CN=CN,
∴△CDN≌△CBN.
∴DN=BN,∠CDN=∠B.
∴∠MDN=∠CDM+∠CDN=∠A+∠B=90°.
∴在Rt△MDN中,由勾股定理,
得MN2=DM2+DN2.即MN2=AM2+BN2.
(2)关系式MN2=AM2+BN2仍然成立.
证明:将△ACM沿直线CE对折,得△GCM,连GN,
则△GCM≌△ACM.
有CG=CA,GM=AM,
∠GCM=∠ACM,∠CGM=∠CAM.
又由CA=CB,得 CG=CB.
由∠GCN=∠GCM+∠ECF=∠GCM+45°,
∠BCN=∠ACB﹣∠ACN=90°﹣(∠ECF﹣∠ACM)=45°+∠ACM.
得∠GCN=∠BCN.
又CN=CN,
∴△CGN≌△CBN.
有GN=BN,∠CGN=∠B=45°,∠CGM=∠CAM=180°﹣∠CAB=135°,
∴∠MGN=∠CGM﹣∠CGN=135°﹣45°=90°.
∴在Rt△MGN中,由勾股定理,
得MN2=GM2+GN2.即MN2=AM2+BN2.
【解题技法】利用“半角”模型2,正确作出辅助线,构造直角三角形是解题的关键。
实战演练:
在等腰△ABC中,CA=CB,点D,E在射线AB上,不与A,B重合(D在E的左边),且∠DCE=∠ACB.21*cnjy*com21教育网21教育名师原创作品【来源:21cnj*y.co*m】
(1)如图1,若∠ACB=90°,将△CAD沿CD翻折,点A与M重合,求证:△MCE≌△BCE;
(2)如图2,若∠ACB=120°,且以AD、DE、EB为边的三角形是直角三角形,求的值;
(3)∠ACB=120°,点D在射线AB上运动,AC=3,则AD的取值范围为 .
(三)正方形中90含45半角模型
条件:正方形ABCD中,∠MAN =45 ,旋转△ABF至△AND;
结论1:△AFM△AMN
结论2: MN=BM+DN(MN=DN-BM)
结论3:C?MCN=2AB;
结论4: ()
典例精讲:
(1)(发现证明)
如图1,在正方形ABCD中,点E_???F?????????B_C,CD边上的动点,且∠EAF=45°,求证:EF=DF+BE.21·世纪*教育网2-1-c-n-j-y21*cnjy*com21教育网
小明发现,当把△ABE_??????Aé?????é??_旋转90°至△ADG,使AB与AD重合时能够证明,请你给出证明过程.www-2-1-cnjy-com21cnjy.com【版权所有:21教育】
(2)(类比引申)①_??????2?????¨???_方形ABCD中,如果点E,F分别是CB,DC延长线上的动点,且∠EAF=45°,则(1)中的结论还成立吗?请写出证明过程.
②如图3,如果点E,F分别是BC_???CD???é?????_上的动点,且∠EAF=45°,则EF,BE,DF之间的数量关系是 (不要求证明)21教育名师原创作品
(3)(联想拓展)如图1,若正方形ABCD的边长为6,AE=3,求AF的长.
【思路点拨】
(1)(发现证明)根据“半角”模型3,证明出△EAF≌△GAF,再根据“半角”模型3的结论2即可得证;21教育名师原创作品
(2)(类比引申)①根据“半角”模型3,证明出△EAF≌△GAF,再根据“半角”模型3的结论2即可得证;21*cnjy*com
②根据“半角”模型3,证明△AFE≌△ANE,再根据“半角”模型3的结论2即可得证;
(3)(联想拓展)
求出DG=2,设DF=x,则根据_??????è§?????¨????_3的结论2得出EF=DG=x+3,CF=6﹣x,在Rt△EFC中,得出关于x的方程,解出x则可得解.
【详解】
(1)(发现证明)
证明:把△ABE绕点A顺时针旋转90°至△ADG,如图1,
∴∠BAE=∠DAG,AE=AG,
∵∠EAF=45°,
∴∠BAE+∠FAD=45°,
∴∠DAG+∠FAD=45°,
∴∠EAF=∠FAG,
∵AF=AF,
∴△EAF≌△GAF(SAS),
∴EF=FG=DF+DG,
∴EF=DF+BE;
(2)(类比引申)
①不成立,结论:EF=DF﹣BE;
证明:如图2,将△ABE绕点A顺时针旋转90°至△ADM,
∴∠EAB=∠MAD,AE=AM,∠EAM=90°,BE=DM,
∴∠FAM=45°=∠EAF,
∵AF=AF,
∴△EAF≌△MAF(SAS),
∴EF=FM=DF﹣DM=DF﹣BE;
②如图3,将△ADF绕点A逆时针旋转90°至△ABN,
∴AN=AF,∠NAF=90°,
∵∠EAF=45°,
∴∠NAE=45°,
∴∠NAE=∠FAE,
∵AE=AE,
∴△AFE≌△ANE(SAS),
∴EF=EN,
∴BE=BN+NE=DF+EF.
即BE=EF+DF.
故答案为:BE=EF+DF.
(3)(联想拓展)
解:由(1)可知AE=AG=3,
∵正方形ABCD的边长为6,
∴DC=BC=AD=6,
∴==3.
∴BE=DG=3,
∴CE=BC﹣BE=6﹣3=3,
设DF=x,则EF=DG=x+3,CF=6﹣x,
在Rt△EFC中,∵CF2+CE2=EF2,
∴(6﹣x)2+32=(x+3)2,
解得:x=2.
∴DF=2,
∴AF===2.
【解题技法】“半角”模型3,常与旋转的性质、全等三角形的判定与性质以及勾股定理的综合应用,将分散的条件集中起来,将隐秘的关系显现出来.
实战演练:
1、思维探索:
在正方形ABCD中,AB=4,∠EAF的两边分别交射线CB,DC于点E,F,∠EAF=45°.
(1)如图1,当点E,F分别在线段BC,CD上时,△CEF的周长是 8 ;
(2)如图2,当点E,F分别在CB,DC的延长线上,CF=2时,求△CEF的周长;
拓展提升:如图3,在R_t???ABC???_,∠ACB=90°,CA=CB,过点B作BD⊥BC,连接AD,在BC的延长线上取一点E,使∠EDA=30°,连接AE,当BD=2,∠EAD=45°时,请直接写出线段CE的长度.21cnjy.com21·cn·jy·com21·世纪*教育网
2、(1)如图,在正_??????_ABC_D 中,∠FAG=45°,请直接写出 DG,BF 与FG 的数量关系,不需要证明.21·cn·jy·com【来源:21·世纪·教育·网】2-1-c-n-j-y21cnjy.com
(2)如图,在__Rt???AB_C 中,∠BAC=90°,AB=AC,E,F 分别是 BC 上两点,∠EAF=45°,【出处:21教育名师】21*cnjy*comwww.21-cn-jy.com
①写出 BE,CF,EF 之间的数量关系,并证明.
②若将(2)中的△AE_F_??????_A_ 旋转至如图所示的位置,上述结论是否仍然成立? 若不成立,直接写出新的结论 ,无需证明.【版权所有:21教育】【来源:21·世纪·教育·网】
(3)如图,△AEF 中∠EAF=45°,AG⊥EF 于 G,且GF=2,GE=3,则 = .
(四)等边三角形中60含30半角模型
条件:△ABC是等边三角形,∠DAE =30 ,旋转△ABD至△ACF;
结论1:△ADE△AFE
结论2:∠ECF =120
结论3:C?ECF=AB;
典例精讲:
转前后的线段之间、角之间的关系进行了探究.
(一)尝试探究
如图1所示,在四边形ABCD中,_AB???AD???_∠BAD=60°,∠ABC=∠ADC=90°,点E、F分别在线段BC、CD上,∠EAF=30°,连接EF.【来源:21cnj*y.co*m】
(1)如图2所示,将△ABE绕点_Aé?????é?????è??_60°后得到△A′B′E′(A′B′与AD重合),请直接写出∠E′AF= 度,线段BE、EF、FD之间的数量关系为 .
(2)如图3,当点E、F分别在线_???BC???CD_的延长线上时,其他条件不变,请探究线段BE、EF、FD之间的数量关系,并说明理由.21教育名师原创作品
(二)拓展延伸
如图4,在等边△ABC中,E_???F???è??BC_上的两点,∠EAF=30°,BE=1,将△ABE绕点A逆时针旋转60°得到△A′B′E′(A′B′与AC重合),连接EE′,AF与EE′交于点N,过点A作AM⊥BC于点M,连接MN,求线段MN的长度.
【思路点拨】
(一)(1)(发现证明)根据“半角”模型4,证明出△AEF≌△AE′F,进而根据线段的和差关系得出结论;【来源:21·世纪·教育·网】
(2)先在BE上截取BG=DF,连接AG,根据“半角”模型4,判定△GAE≌△FAE,根据线段的和差关系得出结论;www-2-1-cnjy-com
(二)先根据“半角”模型4,判定△AEE′是等边三角形,进而得到和∠BAE=∠MAN,最后判定△BAE∽△MAN,并根据相似三角形对应边成比例,列出比例式求得MN的长.【版权所有:21教育】
解:(一)(1)将△ABE绕点A逆时针旋转60°后得到△A′B′E′,
则∠BAE=∠DAE',BE=DE′,AE=AE′,
∵∠BAD=60°,∠EAF=30°,
∴∠BAE+∠DAF=30°,
∴∠DAE'+∠DAF=30°,即∠FAE′=30°
∴∠EAF=∠FAE′,
在△AEF和△AE′F中,,
∴△AEF≌△AE′F(SAS),
∴EF=E′F,即EF=DF+DE′,
∴EF=DF+BE,即线段BE、EF、FD之间的数量关系为BE+DF=EF,
故答案为:30,BE+DF=EF;
(2)如图3,在BE上截取BG=DF,连接AG,
在△ABG和△ADF中,,
∴△ABG≌△ADF(SAS),
∴∠BAG=∠DAF,且AG=AF,
∵∠DAF+∠DAE=30°,
∴∠BAG+∠DAE=30°,
∵∠BAD=60°,
∴∠GAE=60°﹣30°=30°,
∴∠GAE=∠FAE,
在△GAE和△FAE中,,
∴△GAE≌△FAE(SAS),
∴GE=FE,
又∵BE﹣BG=GE,BG=DF,
∴BE﹣DF=EF,
即线段BE、EF、FD之间的数量关系为BE﹣DF=EF;
(二)如图4,将△ABE绕点A逆时针旋转60°得到△A′B′E′,则
AE=AE′,∠EAE′=60°,
∴△AEE′是等边三角形,
又∵∠EAF=30°,
∴AN平分∠EAE',
∴AN⊥EE′,
∴RtANE中,,
∵在等边△ABC中,AM⊥BC,
∴∠BAM=30°,
∴,且∠BAE+∠EAM=30°,
∴,
又∵∠MAN+∠EAM=30°,
∴∠BAE=∠MAN,
∴△BAE∽△MAN,
∴,即,
∴MN=.
【解题技法】根据“半角”模型,对图形进行分解、组合,抓住图形旋转前后的对应边相等,一般解题方法为作辅助线构造全等三角形或相似三角形.
实战演练:
(1)问题背景:
如图1:在四边形ABCD中,AB_???AD??????B_AD=120°,∠B=∠ADC=90°,E、F分别是BC,CD上的点且∠EAF=60°,探究图中线段BE、EF、FD之间的数量关系.21教育网21·世纪*教育网21教育网21·世纪*教育网
小王同学探究此问题的方法是,延_é??FD??°???G_.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;2·1·c·n·j·y21*cnjy*comwww-2-1-cnjy-com21*cnjy*com
(2)探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论 仍然成立(填“是”或“否”);
结论应用:
如图3,在某次_??????????????????_舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以45海里/小时的速度前进,同时舰艇乙沿北偏东50°的方向以60海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两地分别到达E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
能力提高:
如图4,等腰直角三角形ABC中,_???BAC???9_0°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为 .
_21?????????è?????(www.21cnjy.com)_
同课章节目录
