【备战2021年中考数学几何模型汇编专练】专题一 角平分线模型 复习教案
文档属性
| 名称 | 【备战2021年中考数学几何模型汇编专练】专题一 角平分线模型 复习教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-30 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
角平分线常见解题模型
角平分线作为图形最基础的概念_,??¨é?????é??,_填空题和几何证明题中屡见不鲜,同学们除了掌握角平分线的概念和性质定理以外,还需要对常见的角平分线的模型进行了解,在与平行线、三角形、四边形、圆等背景知识的基础上,结合角平分线得到一些常见的结论并对此进行整理记忆.21cnjy.com21教育网21教育网21世纪教育网版权所有
对此将角平分线的常见模型分为如_??????????¨????,_其中前五模块为基础模块,需要同学们掌握其中结论的证明步骤,第六模块为补充模块,只需要了并会运用即可.
模型一:角分线与圆周角和角的n等分线
①角分线与圆周角
模型分析:
如图,直线AB、_CD???è????????_O,OE⊥AB于点O,OF平分∠AOE,∠1=15°30’,则下列结论不正确的是( )21*cnjy*com21·cn·jy·com21cnjy.com
A.∠AOD与∠1互为补角 B.∠1的余角等于74°30′
C.∠2=45° D.∠DOF=135°
【解析】
解:A、∠AOD与∠1互为补角,说法正确;
B、∠1的余角:90°-15°30′=74°30′,说法正确;
C、∵OE⊥AB,
∴∠AOE=90°,
∵OF平分∠AOE,
∴∠2=45°,说法正确;
D、∠DOF=180°-45°-15°30′=119°30′,原题说法错误;
故选:D.
解题通法:掌握余角,补角,角平分线,垂线的性质,通过加减运算解决问题
模型精练:
1.如图,直线AB,CD相交于点O,射线OM平分,,若,则的度数为( )
A.
B.
C.
D.
【答案】C
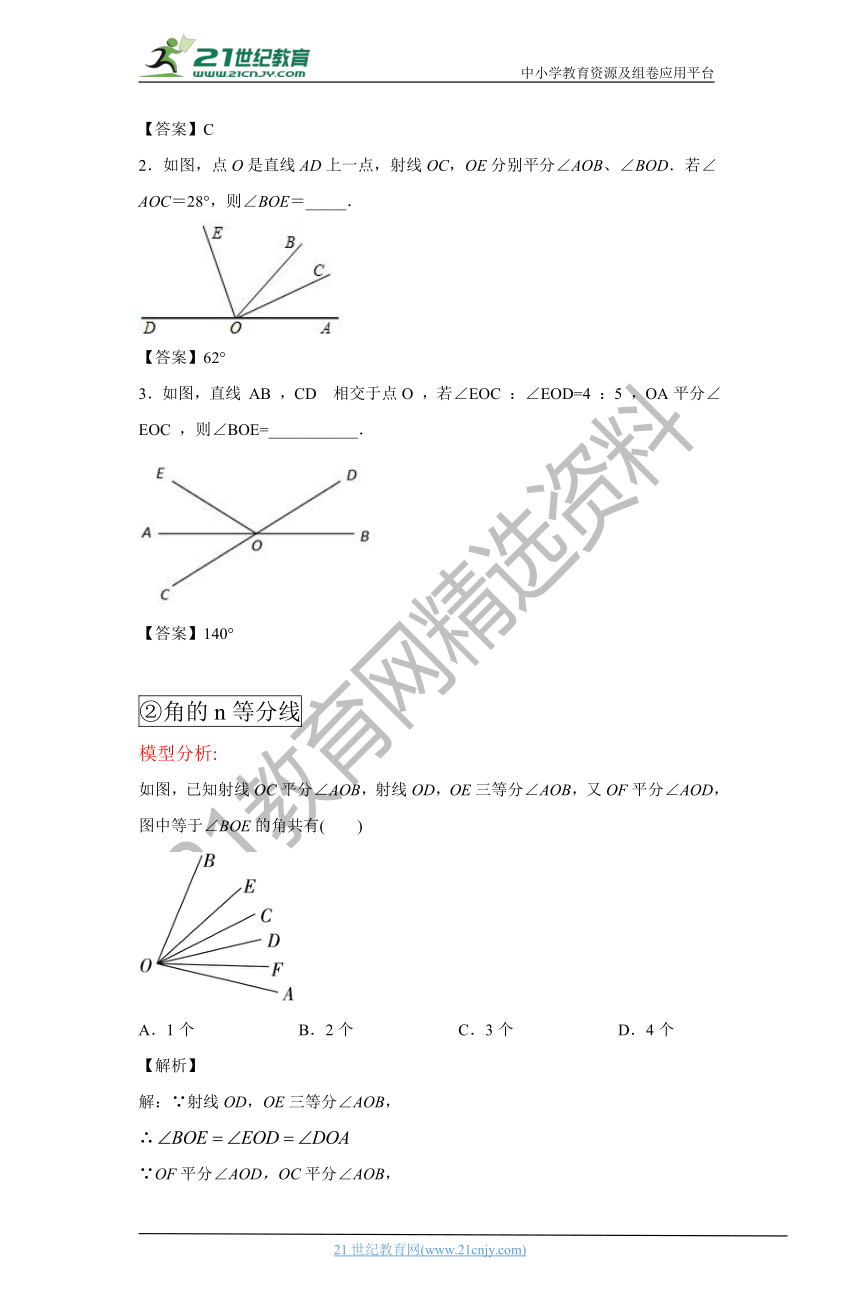
2.如图,点O是直线A_D?????????????°?_线OC,OE分别平分∠AOB、∠BOD.若∠AOC=28°,则∠BOE=_____.【来源:21·世纪·教育·网】21教育网
【答案】62°
3.如图,直线 AB _???CD__???_交于点O ,若∠EOC :∠EOD=4 :5 ,OA平分∠EOC ,则∠BOE=___________.21教育网2-1-c-n-j-y2·1·c·n·j·y
【答案】140°
②角的n等分线
模型分析:
如图,已知射_???OC?????????_AOB,射线OD,OE三等分∠AOB,又OF平分∠AOD,图中等于∠BOE的角共有( )2-1-c-n-j-y2·1·c·n·j·y21*cnjy*com21·世纪*教育网
A.1个 B.2个 C.3个 D.4个
【解析】
解:∵射线OD,OE三等分∠AOB,
∴
∵OF平分∠AOD,OC平分∠AOB,
∴
又∵射线OD,OE三等分∠AOB,
∴
∴,共3个
故选:C.
解题通法:∠A的n等分线=,结合图形的性质进行和差计算;当角平分线累计平分时∠A=.
模型精练:
1.如图所示,已知∠AOB=6_4?°???OA1_平分∠AOB,OA2平分∠AOA1,OA3平分∠AOA2,OA4平分∠AOA3,则∠AOA4的大小为( )2·1·c·n·j·y
A.1° B.2° C.4° D.8°
【答案】C
2.已知:直线,点是直线上不与点重合的一点,连接,.
(1)如图1,当点在射线上时,若,,则___________.
(2)如图2,当点在射线上时,若,求的度数;
(3)若点是直线上不与点重合的一点,当,,时,请直接用含的代数式表示的度数.
【答案】(1);(2);(3).
3.如图1所示的图形,像我们常见的符号——箭号.我们不妨把这样图形叫做“箭头四角形”.
探究:
(1)观察“箭头四角形”,试探究与、、之间的关系,并说明理由;
应用:
(2)请你直接利用以上结论,解决以下两个问题:
①如图2,把一块三角尺放置在上,使三角尺的两条直角边、恰好经过点、,若,则 ;
②如图3,、的2等分线(即角平分线)、相交于点,若,
,求的度数;
拓展:
(3)如图4,,分别是、的2020等分线(),它们的交点从上到下依次为、、、…、.已知,,则 度.
【答案】(1),理由见详解; (2)①30;②95°;(3)
4.如图,,OC是的平分线,是的平分线,是的平分线……是的平分线,则的度数为________.【版权所有:21教育】21·cn·jy·com【出处:21教育名师】2-1-c-n-j-y
【答案】×60°.
模型二:角平分线与三角形(常见辅助线构造全等三角形)
①垂两边
模型分析:
BO是∠ABC的平分线_???è?????O???O_E⊥AB于点E,OF⊥BC于点F,则OE=OF,△BEO≌△BFO.21·世纪*教育网【版权所有:21教育】21·cn·jy·com
解题通法: 由角平分线的性质定理,角平分线上的点到角两边的距离相等,构造全等三角形
模型精练:
1.如图,∠D=∠_C???90?°???_点E是DC的中点,AE平分∠DAB,∠DEA=28°,求∠ABE的大小.2-1-c-n-j-ywww-2-1-cnjy-com【出处:21教育名师】
【答案】28°
2.已知OP平分∠AOB,∠DCE的顶点C在射线OP上,射线CD交射线OA于点F,射线CE交射线OB于点G.21世纪21世纪教育网有【版权所有:21教育】
(1)如图1,若CD⊥OA,CE⊥OB,请直接写出线段CF与CG的数量关系;
(2)如图2,若∠AOB=120?,∠DCE=∠AOC,试判断线段CF与CG的数量关系,并说明理由.21教育名师原创作品21教育名师原创作品
【答案】(1)CF=CG;(2)CF=CG
3.如图,在△OBC中,边BC的垂直平分线交∠BOC的平分线于点D,连接DB,DC,过点D作DF⊥OC于点F.
(1)若∠BOC=60°,求∠BDC的度数;
(2)若∠BOC=,则∠BDC= ;(直接写出结果)
(3)直接写出OB,OC,OF之间的数量关系.
【答案】(1)120°;(2)180°-α;(3)OB+OC=2OF
②截长补短构造全等三角形
模型分析:
在△ABC中,BC>BA,BO是∠ABC的平分线.
(截长法)在BC上取线段BE=BA,连接OE,则△BEO≌△BAO;
(补短法)延长BA至点D,使BD=BC,连接OD,则△BDO≌△BCO.
解题通法: 遇到角平分线时,我们通常过角平分线上的一点向两边作垂线或在角平分线的两端取相等的线段(截长或补短)构造全等三角形.
模型精练:
1.如图,四边_???ABCD???_,AD∥BC,点E在CD上,EA,EB分别平分∠DAB和∠CBA,设AD=x,BC=y且(x﹣3)2+|y﹣4|=0.求AB的长.
【答案】7
2.如图,已知:在△A_BC??????AD_平分∠BAC,AB=AD,CE⊥AD,交AD的延长线于E.求证:AB+AC=2AE.21*cnjy*com
【答案】详见解析
③角平分线+平行线=等腰三角形
模型分析:
由平行线得到内错角相等,由角平分线得到相等的角,等量代换进行解题.
解题通法:平行线与角分线组合在一起会得到等腰三角形.
模型精练:
1.(2017启正单元考)_???????????¨???A_BC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若FG=4,ED=8,求EB+DC=_________.
【答案】12
2.如图,?ABCD中_???AB???3c_m,BC=5cm,BE平分∠ABC交AD于E点,CF平分∠BCD交AD于F点,则EF的长为_____m.21·世纪*教育网
【答案】1
3.如图,已知,平分,,则( )
A. B. C. D.
【答案】B
4.如图,△ABC中,_BD???_???__ABC的角平分线,DE ∥ BC,交AB 于 E,∠A=60?, ∠BDC=95?,则∠BED的度数是( )21·cn·jy·com
A.35° B.70° C.110° D.130°
【答案】C
5.如图,已知△ABC_?????¤è??AB=_5,AC=8,BO、CO分别平分∠ABC、∠ACB,过点O作DE∥BC,则△ADE的周长等于________________.
【答案】13
6.如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.【版权所有:21教育】
(1)图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.
(2)如图②,若AB≠AC,_??????????????????_,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?21·世纪*教育网21世纪21世纪教育网有
(3)如图③,若△ABC中∠B的_?????????BO???_三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.21教育名师原创作品
【答案】(1)_???AEF??????_OEB、△OFC、△OBC、△ABC共5个,EF=BE+FC;(2)有,△EOB、△FOC,存在;(3)有,EF=BE-FC.
7.如图,在矩形中,,,点为边上的一个动点、过点作交边于点,把线段绕点旋转至(点与点对应),点落在线段上,若恰好平分,则的长为_________.
【答案】4
④三线合一(中垂线)
模型分析:
BO是∠ABC的平分线,EF⊥BO,则△BEO≌△BFO.
解题通法:角平分线,高线,中线其中两者重合时也能得到另外的一条件,即此时三线合一,角平分线的所有性质均可使用.21教育名师原创作品
模型精练:
1.如图,在中,,,平分,于,交于.求证:(1);(2).
【答案】(1)证明见解析;(2)证明见解析.
2.如图,,平分,直尺与垂直,则∠1等于_________.
【答案】
模型三:内外角平分线的夹角
①两内角平分线的夹角
在三角形ABC中,∠ABC和∠ACB的平分线BE,CF交于点G,则∠BGA和∠A之间的关系是:∠BGC=90°+∠A
解题通法: 三角形两内角的平分线的夹角等于90°与第三个内角的一半的和.(当两直线平行时,同旁内角的角分线夹角=90°)
模型精练:
1.如图,在四边形ABCD中,∠A=140°,∠D=90°,OB平分∠ABC,OC平分∠BCD,则∠BOC=( )
A.105° B.115° C.125° D.135°
【答案】B
2.如图,AB∥CD,PE平分∠BEF,PF平分∠DFE,若EF=13,PE=12,PF=5.点P到EF的距离为_____.
【答案】
3.如图,在中,和的平分线相交于点,过点作 交于,交于,过点作于,下列四个结论:
①;
②;
③点到各边的距离相等;
④设,,则.
其中正确的结论有( )
A.①②④ B.①②③ C.①③④ D.①②③④
【答案】B
②两外角平分线的夹角
模型分析:
如图,在△ABC中,BO,CO是△ABC的外角平分线,则∠O与∠A之间的关系为:∠O=90°-∠A.21世纪教育网21-cn-jy.com【来源:21cnj*y.co*m】
解题通法: 三角形两外角的平分线的夹角等于90°与第三个内角的一半的差.
模型精练:
1.如图,在△ABC中_??????B???46_°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=_____.【来源:21cnj*y.co*m】
【答案】67°.
2.认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究1:如图l,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90+∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线
∴∠1=∠ABC, ∠2=∠ACB
∴∠l+∠2=(∠ABC+∠ACB)= (180-∠A)= 90-∠A
∴∠BOC=180-(∠1+∠2) =180-(90-∠A)=90+∠A
(1)探究2;如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
(2)探究3:如图3中, O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(直接写出结论)
(3)拓展:_??????4?????¨???_边形ABCD中,O是∠ABC与∠DCB的平分线BO和CO的交点,则∠BOC与∠A+∠D有怎样的关系?(直接写出结论)
【答案】(1)探究2结论:∠BOC=;(2)探究3:结论∠BOC=90°-;(3)拓展:结论
3.(1)如图(a),平分,平分.
①当时,求的度数.
②猜想与有什么数量关系?并证明你的结论.
(2)如图(b),平分外角,平分外角,(1)中②的猜想还正确吗?如果不正确,请你直接写出正确的结论(不用写出证明过程).
【答案】(1)①120°;②;证明见解析;(2)不正确;
4.(1)探究1:如图1,P是_???ABC??????_角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=70?,则∠BPC=_______度;21*cnjy*com
(2)探究2:如图2,P是△ABC的外角∠DBC与外角∠ECB的平分线BP和CP的交点,求∠BPC与∠A的数量关系?并说明理由。www-2-1-cnjy-com
(3)拓展:如图3,P是四_è?????ABCD_的外角∠EBC与∠BCF的平分线BP和CP的交点,设∠A+∠D=α.,直接写出∠BPC与α的数量关系;
【答案】(1)125°;(2)∠BPC=90°﹣∠A,理由见解析;(3)∠BPC =180°﹣
③一个内角一个外角平分线的夹角
模型分析:
如图,在△ABC中,BP平分∠ABC,CP平分∠ACB的外角,两条角平分线相交于点P,则∠P与∠A之间的关系是:∠P=21世纪教育网21-cn-jy.com
解题通法: 三角形一内角与另一外角的平分线的夹角等于第三个内角的一半.当该条件累计平分时得到夹角=(n为累计平分的次数)21*cnjy*com
模型精练:
1.如图,在中,,和的平分线交于点,得;和的平分线交于点,得和的平分线交于点,则__________度.【出处:21教育名师】
【答案】
2.如图,,的平分线相交于点,的平分线相交于点,,的平分线相交于点……以此类推,则的度数是___________(用含与的代数式表示).
【答案】
3.如图,在△ABC中,∠_A=60?°???_BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.
【答案】15°
4.认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
(1)如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,试证明∠BOC=90°+
(2)如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
(3)如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
【答案】(1)见解析;(2)∠BOC=,理由见解析;(3)∠BOC=90°-
④内角平分线与高线的夹角
模型分析:
如图,在△ABC中,AE平分∠BAC,AD⊥BC,则∠EAD=|∠B-∠C|(绝对值是因为不确定AE与AD的位置)
解题通法:三角形同一顶点的角分线与高线的夹角=两底角差的绝对值的一半
模型精练:
1.如图所示,在中,是高,、是角平分线,它们相交于点,,,求、的度数.
【答案】,
2.如图,在中,、分别是的高和角平分线,,,则__________度.
【答案】5
3.如图,在△ABC中,∠B__=_60?°_,∠C = 40°,AE平分∠BAC,AD⊥BC,垂足为点D,那么∠DAE =______度.21cnjy.com【来源:21·世纪·教育·网】
【答案】10
模型四:角平分线在矩形中的应用
①矩形的翻折
模型分析:
如图,把一张长方形的纸片ABCD沿EF折叠,若∠AED′=40°,则∠DEF的度数为( )
A.40° B.50° C.60° D.70°
【解析】
解:由翻折不变性可知:∠DEF=∠FED′,
∵∠AED′=40°,
∴∠DED′=140°,
∴∠DEF=∠DED′=70°,
故选D.21*cnjy*com
解题通法:矩形的翻折遵_??§?????????????§°_的原则,折痕就是对称轴,即角平分线所在的直线,;矩形的翻折中默认存在直角,这一结论在求角度时常结合两锐角互余,当在求边的长度是常结合勾股定理求解.www-2-1-cnjy-com
模型精练:
1.长方形如图折叠,D点折叠到的位置,已知∠FC=40°,则∠EFC=( )
A.120° B.110° C.105° D.115°
【答案】B
2.如图,将长方形纸片ABC_D??????C??????_GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部的点E处,若FH平分∠BFE,则∠GFH的度数是____.?
【答案】90°
3.把长方形纸片AB_CD??????è§????_AC折叠,得到如图所示的图形,AD平分∠B′AC,则∠B′CD=______.【来源:21cnj*y.co*m】【来源:21cnj*y.co*m】
【答案】30°
4.如图折叠一张矩形纸片,已知∠1=70°,则∠2的度数是__.
【答案】55°
5.如图a是长方形纸带,_???DEF=2_5°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是____________°.
【答案】105°
6.如图1,在长方形纸片ABCD中,E点在边AD上,F、G分别在边AB、CD上,分别以EF、EG为折痕进行折叠并压平,点A、D的对应点分别是点A′和点D′,若ED′平分∠FEG,且在内部,如图2,设∠A′ED'=n°,则∠FE D′的度数为___________(用含n的代数式表示).2·1·c·n·j·y
【答案】
模型五:角平分线在圆中的应用
①圆外一点的切线 (切线长定理)
模型分析:
如图,P为圆外一点,过点p作圆O的两条切线,则PA=PB.
解题通法:用HL证明直角三角形的全等,由全等的性质得到角平分线,这一过程也说明角平分线上的点到角两边的距离相等.【出处:21教育名师】
模型精练:
1.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P的度数.
【答案】40°
2.已知:PA、PB、CD分别切⊙O于A、B、E三点,PA=6.求:
(1)△PCD的周长;
(2)若∠P=50°,求∠COD的度数.
【答案】(1)12;(2) 65°.
3.如图,AB是直径,分别过上点B,C的切线,且,连接AC.求的度数.
【答案】35
4.如图,在中,,点为上一点,以点为圆心,为半径的与相切于点,交的延长线于点.
求证:;
5.如图,PA、PB是⊙_O????????????A_、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.www-2-1-cnjy-com
(1)求证:四边形ACBP是菱形;
(2)若⊙O半径为1,求菱形ACBP的面积.
【答案】(1).证明见解析;(2)菱形ACBP的面积=.
②内心(内角平分线)与面积
模型分析:
圆O是三角形ABC的内接三角形,此时称点O是三角形ABC的内心,则
解题通法:三角形的内心通常结合三角形的面积与周长一起考查,常常通过角平分先性质定理得到半径相等作为突破口,结合面积公式求解.
模型精练:
1.已知:如图,、是的切线,切点分别是、,为上一点,过点作的切线,交、于、点,已知,求的周长.21世纪21世纪教育网有21世纪教育网21-cn-jy.com21cnjy.com21*cnjy*com
【答案】的周长是.
2.我们知道,与三角形各边都相切的圆叫做三角形的内切圆,则三角形可以称为圆的外切三角形.如图1,与的三边分别相切于点则叫做的外切三角形.以此类推,各边都和圆相切的四边形称为圆外切四边形.如图2,与四边形ABCD的边分别相切于点则四边形叫做的外切四边形.21*cnjy*com
(1)如图2,试探究圆外切四边形的两组对边与之间的数量关系,猜想: (横线上填“>”,“<”或“=”);
(2)利用图2证明你的猜想(写出已知,求证,证明过程);
(3)用文字叙述上面证明的结论: ;
(4)若圆外切四边形的周长为相邻的三条边的比为,求此四边形各边的长.
【答案】(1)=;(2)答案见解析;(3)圆外切四边形的对边之和相等;(4)4;10;12;6
3.已知:如图,分别切于点点.
(1)若,求;
(2)若,求的周长.
【答案】(1)70°;(2)
4.已知PA,PB分别切⊙O于A,B,E为劣弧AB上一点,过E点的切线交PA于C,交PB于D.
(1)若PA=6,求△PCD的周长;
(2)若∠P=50°,求∠DOC.
【答案】(1)△PCD的周长为12;(2)∠DOC=65°.
5.如图,已知△AB_C?????¨é?????2_1,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是_____.【来源:21·世纪·教育·网】
【答案】42
6.如图,已知⊙O为Rt△ABC的内切圆,切点分别为D,E,F,且∠C=90°,AB=13,BC=12.【来源:21·世纪·教育·网】www.21-cn-jy.com
(1)求BF的长;
(2)求⊙O的半径r.
【答案】(1)BF=10;(2)r=2.
7.如图,△ABC中,∠B_AC???90?°_,∠B=30°,BC边上有一点P(不与点B,C重合),I为△APC的内心,若∠AIC的取值范围为m°<∠AIC<n°,则m+n=_____.
【答案】255.
模型六:内角平分线定理和外角平分线定理
①内角平分线定理
模型分析:
在△ABC中,若AD是∠BAC的平分线,
求证:AB:AC=BD:CD
证明: 分别以AB、AC_??????_计算△ABD的_é???§?_与△ACD的面积
由于高相等(角平分线上任意一点_??°è§?_的两边距离相等)
因此S△ABD:S△ACD=AB:AC
又因为S△ABD:S△ACD=BD:CD(分别以BD、CD为底,高相同)。
所以AB:AC=BD:CD
解题通法: 三角形内角平分线分_???è??_所成的两条_??????_,和两条邻边成比例.
模型精练:
1.如图,在中,,,是的平分线,,垂足是,和的延长线交于点.
(1)在图中找出与全等的三角形,并说出全等的理由;
(2)说明;
(3)如果,直接写出的长为 .
【答案】(1)见解析;(2)见解析;(3)5﹣5.
②外角平分线定理
模型分析:
△ABC中,∠BAC的外角平分线交BC的延长线于点D,
求证:BD︰CD=AB︰AC。
证明:过C作AD的平行线交AB于点E。
∵EC//AD
∴BD︰CD=AB︰AE,∠1=∠3,∠2=∠4
∵AD为∠BAC的外角平分线
∴∠1=∠2
∴∠3=∠1=∠2=∠4
∴AE=AC
∴BD︰CD=AB︰AC
解题通法: 三角形两边之比等于其夹角的外角平分线外分对边之比
_21?????????è?????(www.21cnjy.com)_
角平分线常见解题模型
角平分线作为图形最基础的概念_,??¨é?????é??,_填空题和几何证明题中屡见不鲜,同学们除了掌握角平分线的概念和性质定理以外,还需要对常见的角平分线的模型进行了解,在与平行线、三角形、四边形、圆等背景知识的基础上,结合角平分线得到一些常见的结论并对此进行整理记忆.21cnjy.com21教育网21教育网21世纪教育网版权所有
对此将角平分线的常见模型分为如_??????????¨????,_其中前五模块为基础模块,需要同学们掌握其中结论的证明步骤,第六模块为补充模块,只需要了并会运用即可.
模型一:角分线与圆周角和角的n等分线
①角分线与圆周角
模型分析:
如图,直线AB、_CD???è????????_O,OE⊥AB于点O,OF平分∠AOE,∠1=15°30’,则下列结论不正确的是( )21*cnjy*com21·cn·jy·com21cnjy.com
A.∠AOD与∠1互为补角 B.∠1的余角等于74°30′
C.∠2=45° D.∠DOF=135°
【解析】
解:A、∠AOD与∠1互为补角,说法正确;
B、∠1的余角:90°-15°30′=74°30′,说法正确;
C、∵OE⊥AB,
∴∠AOE=90°,
∵OF平分∠AOE,
∴∠2=45°,说法正确;
D、∠DOF=180°-45°-15°30′=119°30′,原题说法错误;
故选:D.
解题通法:掌握余角,补角,角平分线,垂线的性质,通过加减运算解决问题
模型精练:
1.如图,直线AB,CD相交于点O,射线OM平分,,若,则的度数为( )
A.
B.
C.
D.
【答案】C
2.如图,点O是直线A_D?????????????°?_线OC,OE分别平分∠AOB、∠BOD.若∠AOC=28°,则∠BOE=_____.【来源:21·世纪·教育·网】21教育网
【答案】62°
3.如图,直线 AB _???CD__???_交于点O ,若∠EOC :∠EOD=4 :5 ,OA平分∠EOC ,则∠BOE=___________.21教育网2-1-c-n-j-y2·1·c·n·j·y
【答案】140°
②角的n等分线
模型分析:
如图,已知射_???OC?????????_AOB,射线OD,OE三等分∠AOB,又OF平分∠AOD,图中等于∠BOE的角共有( )2-1-c-n-j-y2·1·c·n·j·y21*cnjy*com21·世纪*教育网
A.1个 B.2个 C.3个 D.4个
【解析】
解:∵射线OD,OE三等分∠AOB,
∴
∵OF平分∠AOD,OC平分∠AOB,
∴
又∵射线OD,OE三等分∠AOB,
∴
∴,共3个
故选:C.
解题通法:∠A的n等分线=,结合图形的性质进行和差计算;当角平分线累计平分时∠A=.
模型精练:
1.如图所示,已知∠AOB=6_4?°???OA1_平分∠AOB,OA2平分∠AOA1,OA3平分∠AOA2,OA4平分∠AOA3,则∠AOA4的大小为( )2·1·c·n·j·y
A.1° B.2° C.4° D.8°
【答案】C
2.已知:直线,点是直线上不与点重合的一点,连接,.
(1)如图1,当点在射线上时,若,,则___________.
(2)如图2,当点在射线上时,若,求的度数;
(3)若点是直线上不与点重合的一点,当,,时,请直接用含的代数式表示的度数.
【答案】(1);(2);(3).
3.如图1所示的图形,像我们常见的符号——箭号.我们不妨把这样图形叫做“箭头四角形”.
探究:
(1)观察“箭头四角形”,试探究与、、之间的关系,并说明理由;
应用:
(2)请你直接利用以上结论,解决以下两个问题:
①如图2,把一块三角尺放置在上,使三角尺的两条直角边、恰好经过点、,若,则 ;
②如图3,、的2等分线(即角平分线)、相交于点,若,
,求的度数;
拓展:
(3)如图4,,分别是、的2020等分线(),它们的交点从上到下依次为、、、…、.已知,,则 度.
【答案】(1),理由见详解; (2)①30;②95°;(3)
4.如图,,OC是的平分线,是的平分线,是的平分线……是的平分线,则的度数为________.【版权所有:21教育】21·cn·jy·com【出处:21教育名师】2-1-c-n-j-y
【答案】×60°.
模型二:角平分线与三角形(常见辅助线构造全等三角形)
①垂两边
模型分析:
BO是∠ABC的平分线_???è?????O???O_E⊥AB于点E,OF⊥BC于点F,则OE=OF,△BEO≌△BFO.21·世纪*教育网【版权所有:21教育】21·cn·jy·com
解题通法: 由角平分线的性质定理,角平分线上的点到角两边的距离相等,构造全等三角形
模型精练:
1.如图,∠D=∠_C???90?°???_点E是DC的中点,AE平分∠DAB,∠DEA=28°,求∠ABE的大小.2-1-c-n-j-ywww-2-1-cnjy-com【出处:21教育名师】
【答案】28°
2.已知OP平分∠AOB,∠DCE的顶点C在射线OP上,射线CD交射线OA于点F,射线CE交射线OB于点G.21世纪21世纪教育网有【版权所有:21教育】
(1)如图1,若CD⊥OA,CE⊥OB,请直接写出线段CF与CG的数量关系;
(2)如图2,若∠AOB=120?,∠DCE=∠AOC,试判断线段CF与CG的数量关系,并说明理由.21教育名师原创作品21教育名师原创作品
【答案】(1)CF=CG;(2)CF=CG
3.如图,在△OBC中,边BC的垂直平分线交∠BOC的平分线于点D,连接DB,DC,过点D作DF⊥OC于点F.
(1)若∠BOC=60°,求∠BDC的度数;
(2)若∠BOC=,则∠BDC= ;(直接写出结果)
(3)直接写出OB,OC,OF之间的数量关系.
【答案】(1)120°;(2)180°-α;(3)OB+OC=2OF
②截长补短构造全等三角形
模型分析:
在△ABC中,BC>BA,BO是∠ABC的平分线.
(截长法)在BC上取线段BE=BA,连接OE,则△BEO≌△BAO;
(补短法)延长BA至点D,使BD=BC,连接OD,则△BDO≌△BCO.
解题通法: 遇到角平分线时,我们通常过角平分线上的一点向两边作垂线或在角平分线的两端取相等的线段(截长或补短)构造全等三角形.
模型精练:
1.如图,四边_???ABCD???_,AD∥BC,点E在CD上,EA,EB分别平分∠DAB和∠CBA,设AD=x,BC=y且(x﹣3)2+|y﹣4|=0.求AB的长.
【答案】7
2.如图,已知:在△A_BC??????AD_平分∠BAC,AB=AD,CE⊥AD,交AD的延长线于E.求证:AB+AC=2AE.21*cnjy*com
【答案】详见解析
③角平分线+平行线=等腰三角形
模型分析:
由平行线得到内错角相等,由角平分线得到相等的角,等量代换进行解题.
解题通法:平行线与角分线组合在一起会得到等腰三角形.
模型精练:
1.(2017启正单元考)_???????????¨???A_BC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若FG=4,ED=8,求EB+DC=_________.
【答案】12
2.如图,?ABCD中_???AB???3c_m,BC=5cm,BE平分∠ABC交AD于E点,CF平分∠BCD交AD于F点,则EF的长为_____m.21·世纪*教育网
【答案】1
3.如图,已知,平分,,则( )
A. B. C. D.
【答案】B
4.如图,△ABC中,_BD???_???__ABC的角平分线,DE ∥ BC,交AB 于 E,∠A=60?, ∠BDC=95?,则∠BED的度数是( )21·cn·jy·com
A.35° B.70° C.110° D.130°
【答案】C
5.如图,已知△ABC_?????¤è??AB=_5,AC=8,BO、CO分别平分∠ABC、∠ACB,过点O作DE∥BC,则△ADE的周长等于________________.
【答案】13
6.如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.【版权所有:21教育】
(1)图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.
(2)如图②,若AB≠AC,_??????????????????_,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?21·世纪*教育网21世纪21世纪教育网有
(3)如图③,若△ABC中∠B的_?????????BO???_三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.21教育名师原创作品
【答案】(1)_???AEF??????_OEB、△OFC、△OBC、△ABC共5个,EF=BE+FC;(2)有,△EOB、△FOC,存在;(3)有,EF=BE-FC.
7.如图,在矩形中,,,点为边上的一个动点、过点作交边于点,把线段绕点旋转至(点与点对应),点落在线段上,若恰好平分,则的长为_________.
【答案】4
④三线合一(中垂线)
模型分析:
BO是∠ABC的平分线,EF⊥BO,则△BEO≌△BFO.
解题通法:角平分线,高线,中线其中两者重合时也能得到另外的一条件,即此时三线合一,角平分线的所有性质均可使用.21教育名师原创作品
模型精练:
1.如图,在中,,,平分,于,交于.求证:(1);(2).
【答案】(1)证明见解析;(2)证明见解析.
2.如图,,平分,直尺与垂直,则∠1等于_________.
【答案】
模型三:内外角平分线的夹角
①两内角平分线的夹角
在三角形ABC中,∠ABC和∠ACB的平分线BE,CF交于点G,则∠BGA和∠A之间的关系是:∠BGC=90°+∠A
解题通法: 三角形两内角的平分线的夹角等于90°与第三个内角的一半的和.(当两直线平行时,同旁内角的角分线夹角=90°)
模型精练:
1.如图,在四边形ABCD中,∠A=140°,∠D=90°,OB平分∠ABC,OC平分∠BCD,则∠BOC=( )
A.105° B.115° C.125° D.135°
【答案】B
2.如图,AB∥CD,PE平分∠BEF,PF平分∠DFE,若EF=13,PE=12,PF=5.点P到EF的距离为_____.
【答案】
3.如图,在中,和的平分线相交于点,过点作 交于,交于,过点作于,下列四个结论:
①;
②;
③点到各边的距离相等;
④设,,则.
其中正确的结论有( )
A.①②④ B.①②③ C.①③④ D.①②③④
【答案】B
②两外角平分线的夹角
模型分析:
如图,在△ABC中,BO,CO是△ABC的外角平分线,则∠O与∠A之间的关系为:∠O=90°-∠A.21世纪教育网21-cn-jy.com【来源:21cnj*y.co*m】
解题通法: 三角形两外角的平分线的夹角等于90°与第三个内角的一半的差.
模型精练:
1.如图,在△ABC中_??????B???46_°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=_____.【来源:21cnj*y.co*m】
【答案】67°.
2.认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究1:如图l,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90+∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线
∴∠1=∠ABC, ∠2=∠ACB
∴∠l+∠2=(∠ABC+∠ACB)= (180-∠A)= 90-∠A
∴∠BOC=180-(∠1+∠2) =180-(90-∠A)=90+∠A
(1)探究2;如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
(2)探究3:如图3中, O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(直接写出结论)
(3)拓展:_??????4?????¨???_边形ABCD中,O是∠ABC与∠DCB的平分线BO和CO的交点,则∠BOC与∠A+∠D有怎样的关系?(直接写出结论)
【答案】(1)探究2结论:∠BOC=;(2)探究3:结论∠BOC=90°-;(3)拓展:结论
3.(1)如图(a),平分,平分.
①当时,求的度数.
②猜想与有什么数量关系?并证明你的结论.
(2)如图(b),平分外角,平分外角,(1)中②的猜想还正确吗?如果不正确,请你直接写出正确的结论(不用写出证明过程).
【答案】(1)①120°;②;证明见解析;(2)不正确;
4.(1)探究1:如图1,P是_???ABC??????_角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=70?,则∠BPC=_______度;21*cnjy*com
(2)探究2:如图2,P是△ABC的外角∠DBC与外角∠ECB的平分线BP和CP的交点,求∠BPC与∠A的数量关系?并说明理由。www-2-1-cnjy-com
(3)拓展:如图3,P是四_è?????ABCD_的外角∠EBC与∠BCF的平分线BP和CP的交点,设∠A+∠D=α.,直接写出∠BPC与α的数量关系;
【答案】(1)125°;(2)∠BPC=90°﹣∠A,理由见解析;(3)∠BPC =180°﹣
③一个内角一个外角平分线的夹角
模型分析:
如图,在△ABC中,BP平分∠ABC,CP平分∠ACB的外角,两条角平分线相交于点P,则∠P与∠A之间的关系是:∠P=21世纪教育网21-cn-jy.com
解题通法: 三角形一内角与另一外角的平分线的夹角等于第三个内角的一半.当该条件累计平分时得到夹角=(n为累计平分的次数)21*cnjy*com
模型精练:
1.如图,在中,,和的平分线交于点,得;和的平分线交于点,得和的平分线交于点,则__________度.【出处:21教育名师】
【答案】
2.如图,,的平分线相交于点,的平分线相交于点,,的平分线相交于点……以此类推,则的度数是___________(用含与的代数式表示).
【答案】
3.如图,在△ABC中,∠_A=60?°???_BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.
【答案】15°
4.认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
(1)如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,试证明∠BOC=90°+
(2)如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
(3)如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
【答案】(1)见解析;(2)∠BOC=,理由见解析;(3)∠BOC=90°-
④内角平分线与高线的夹角
模型分析:
如图,在△ABC中,AE平分∠BAC,AD⊥BC,则∠EAD=|∠B-∠C|(绝对值是因为不确定AE与AD的位置)
解题通法:三角形同一顶点的角分线与高线的夹角=两底角差的绝对值的一半
模型精练:
1.如图所示,在中,是高,、是角平分线,它们相交于点,,,求、的度数.
【答案】,
2.如图,在中,、分别是的高和角平分线,,,则__________度.
【答案】5
3.如图,在△ABC中,∠B__=_60?°_,∠C = 40°,AE平分∠BAC,AD⊥BC,垂足为点D,那么∠DAE =______度.21cnjy.com【来源:21·世纪·教育·网】
【答案】10
模型四:角平分线在矩形中的应用
①矩形的翻折
模型分析:
如图,把一张长方形的纸片ABCD沿EF折叠,若∠AED′=40°,则∠DEF的度数为( )
A.40° B.50° C.60° D.70°
【解析】
解:由翻折不变性可知:∠DEF=∠FED′,
∵∠AED′=40°,
∴∠DED′=140°,
∴∠DEF=∠DED′=70°,
故选D.21*cnjy*com
解题通法:矩形的翻折遵_??§?????????????§°_的原则,折痕就是对称轴,即角平分线所在的直线,;矩形的翻折中默认存在直角,这一结论在求角度时常结合两锐角互余,当在求边的长度是常结合勾股定理求解.www-2-1-cnjy-com
模型精练:
1.长方形如图折叠,D点折叠到的位置,已知∠FC=40°,则∠EFC=( )
A.120° B.110° C.105° D.115°
【答案】B
2.如图,将长方形纸片ABC_D??????C??????_GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部的点E处,若FH平分∠BFE,则∠GFH的度数是____.?
【答案】90°
3.把长方形纸片AB_CD??????è§????_AC折叠,得到如图所示的图形,AD平分∠B′AC,则∠B′CD=______.【来源:21cnj*y.co*m】【来源:21cnj*y.co*m】
【答案】30°
4.如图折叠一张矩形纸片,已知∠1=70°,则∠2的度数是__.
【答案】55°
5.如图a是长方形纸带,_???DEF=2_5°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是____________°.
【答案】105°
6.如图1,在长方形纸片ABCD中,E点在边AD上,F、G分别在边AB、CD上,分别以EF、EG为折痕进行折叠并压平,点A、D的对应点分别是点A′和点D′,若ED′平分∠FEG,且在内部,如图2,设∠A′ED'=n°,则∠FE D′的度数为___________(用含n的代数式表示).2·1·c·n·j·y
【答案】
模型五:角平分线在圆中的应用
①圆外一点的切线 (切线长定理)
模型分析:
如图,P为圆外一点,过点p作圆O的两条切线,则PA=PB.
解题通法:用HL证明直角三角形的全等,由全等的性质得到角平分线,这一过程也说明角平分线上的点到角两边的距离相等.【出处:21教育名师】
模型精练:
1.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P的度数.
【答案】40°
2.已知:PA、PB、CD分别切⊙O于A、B、E三点,PA=6.求:
(1)△PCD的周长;
(2)若∠P=50°,求∠COD的度数.
【答案】(1)12;(2) 65°.
3.如图,AB是直径,分别过上点B,C的切线,且,连接AC.求的度数.
【答案】35
4.如图,在中,,点为上一点,以点为圆心,为半径的与相切于点,交的延长线于点.
求证:;
5.如图,PA、PB是⊙_O????????????A_、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.www-2-1-cnjy-com
(1)求证:四边形ACBP是菱形;
(2)若⊙O半径为1,求菱形ACBP的面积.
【答案】(1).证明见解析;(2)菱形ACBP的面积=.
②内心(内角平分线)与面积
模型分析:
圆O是三角形ABC的内接三角形,此时称点O是三角形ABC的内心,则
解题通法:三角形的内心通常结合三角形的面积与周长一起考查,常常通过角平分先性质定理得到半径相等作为突破口,结合面积公式求解.
模型精练:
1.已知:如图,、是的切线,切点分别是、,为上一点,过点作的切线,交、于、点,已知,求的周长.21世纪21世纪教育网有21世纪教育网21-cn-jy.com21cnjy.com21*cnjy*com
【答案】的周长是.
2.我们知道,与三角形各边都相切的圆叫做三角形的内切圆,则三角形可以称为圆的外切三角形.如图1,与的三边分别相切于点则叫做的外切三角形.以此类推,各边都和圆相切的四边形称为圆外切四边形.如图2,与四边形ABCD的边分别相切于点则四边形叫做的外切四边形.21*cnjy*com
(1)如图2,试探究圆外切四边形的两组对边与之间的数量关系,猜想: (横线上填“>”,“<”或“=”);
(2)利用图2证明你的猜想(写出已知,求证,证明过程);
(3)用文字叙述上面证明的结论: ;
(4)若圆外切四边形的周长为相邻的三条边的比为,求此四边形各边的长.
【答案】(1)=;(2)答案见解析;(3)圆外切四边形的对边之和相等;(4)4;10;12;6
3.已知:如图,分别切于点点.
(1)若,求;
(2)若,求的周长.
【答案】(1)70°;(2)
4.已知PA,PB分别切⊙O于A,B,E为劣弧AB上一点,过E点的切线交PA于C,交PB于D.
(1)若PA=6,求△PCD的周长;
(2)若∠P=50°,求∠DOC.
【答案】(1)△PCD的周长为12;(2)∠DOC=65°.
5.如图,已知△AB_C?????¨é?????2_1,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是_____.【来源:21·世纪·教育·网】
【答案】42
6.如图,已知⊙O为Rt△ABC的内切圆,切点分别为D,E,F,且∠C=90°,AB=13,BC=12.【来源:21·世纪·教育·网】www.21-cn-jy.com
(1)求BF的长;
(2)求⊙O的半径r.
【答案】(1)BF=10;(2)r=2.
7.如图,△ABC中,∠B_AC???90?°_,∠B=30°,BC边上有一点P(不与点B,C重合),I为△APC的内心,若∠AIC的取值范围为m°<∠AIC<n°,则m+n=_____.
【答案】255.
模型六:内角平分线定理和外角平分线定理
①内角平分线定理
模型分析:
在△ABC中,若AD是∠BAC的平分线,
求证:AB:AC=BD:CD
证明: 分别以AB、AC_??????_计算△ABD的_é???§?_与△ACD的面积
由于高相等(角平分线上任意一点_??°è§?_的两边距离相等)
因此S△ABD:S△ACD=AB:AC
又因为S△ABD:S△ACD=BD:CD(分别以BD、CD为底,高相同)。
所以AB:AC=BD:CD
解题通法: 三角形内角平分线分_???è??_所成的两条_??????_,和两条邻边成比例.
模型精练:
1.如图,在中,,,是的平分线,,垂足是,和的延长线交于点.
(1)在图中找出与全等的三角形,并说出全等的理由;
(2)说明;
(3)如果,直接写出的长为 .
【答案】(1)见解析;(2)见解析;(3)5﹣5.
②外角平分线定理
模型分析:
△ABC中,∠BAC的外角平分线交BC的延长线于点D,
求证:BD︰CD=AB︰AC。
证明:过C作AD的平行线交AB于点E。
∵EC//AD
∴BD︰CD=AB︰AE,∠1=∠3,∠2=∠4
∵AD为∠BAC的外角平分线
∴∠1=∠2
∴∠3=∠1=∠2=∠4
∴AE=AC
∴BD︰CD=AB︰AC
解题通法: 三角形两边之比等于其夹角的外角平分线外分对边之比
_21?????????è?????(www.21cnjy.com)_
同课章节目录
