六安市2011—2012学年高二第一学期期末考试理科数学试卷
文档属性
| 名称 | 六安市2011—2012学年高二第一学期期末考试理科数学试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 158.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-07 14:58:35 | ||
图片预览


文档简介
六安市2011—2012学年第一学期期末考试
高二理科数学试卷
第Ⅰ卷(共50分)
命题:余其权 审题:冯坤兵
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个备选项中,只有一项是符合题目要求的。
1、命题“”的否定为 ( )
A. B.
C. D.
2、若等差数列{}的前三项和且,则等于( )
A.4 B.5 C.6 D.7
3、若,则等于( )
A. B. C. D.
4、 在等比数列中,,则项数为( )
A.3 B.4 C.5 D.6
5、设抛物线的顶点在原点,准线方程为,则抛物线的方程是 ( )
A. B. C. D.
6、在中,,则的形状是( )
A.锐角三角形 B.直角三角形 C. 钝角三角形 D.非钝角三角形
7、已知满足约束条件 则的最大值为( )
A . B. C. D.
8、在中,一定成立的等式是( )
A. B.
C. D.
9、如图:在平行六面体中,若则下列向量中与相等的是( )
A. B.
C. D.
10、椭圆与双曲线有公共的焦点,的一条渐近线与以的长轴为直径的圆交于两点,若将线段三等分,则( )
A. B. C. D.
第Ⅱ卷(共100分)
二、填空题:本大题共5小题,每小题5分,共25分。
11、已知向量,若,则 .
12、已知且满足,则的最小值为 .
13、设双曲线的渐近线方程为,则的值为 .
14、某舰艇在A处测得遇险渔船在北偏东45°距离为10海里的C处,此时得知,该渔船沿东偏南15°方向,以每小时9海里的速度向一小岛靠近,舰艇时速21海里,则舰艇到达渔船的最短时间是 小时.
15、下列命题正确的是 .
①.命题“若,则”的逆否命题为“若,则”。
②.若为假命题,则均为假命题。
③.在中,a,b,c分别是角A,B,C对应的三边,则“是直角三角形”是“”的充要条件。
④.“”是“”的充分不必要条件。
⑤.命题“若,则”的否命题为:“若,则”.
三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.
16、(本小题满分12分)
等比数列中,已知
(Ⅰ)求数列的通项公式;
(Ⅱ)若分别为等差数列的第3项和第5项,求数列的通项公式及前项和。
17、(本小题满分12分)
已知锐角三角形ABC中,边为方程的两根,角A、B满足。
(Ⅰ)求角C与边c ; (Ⅱ)求的面积。
18、(本小题满分12分)
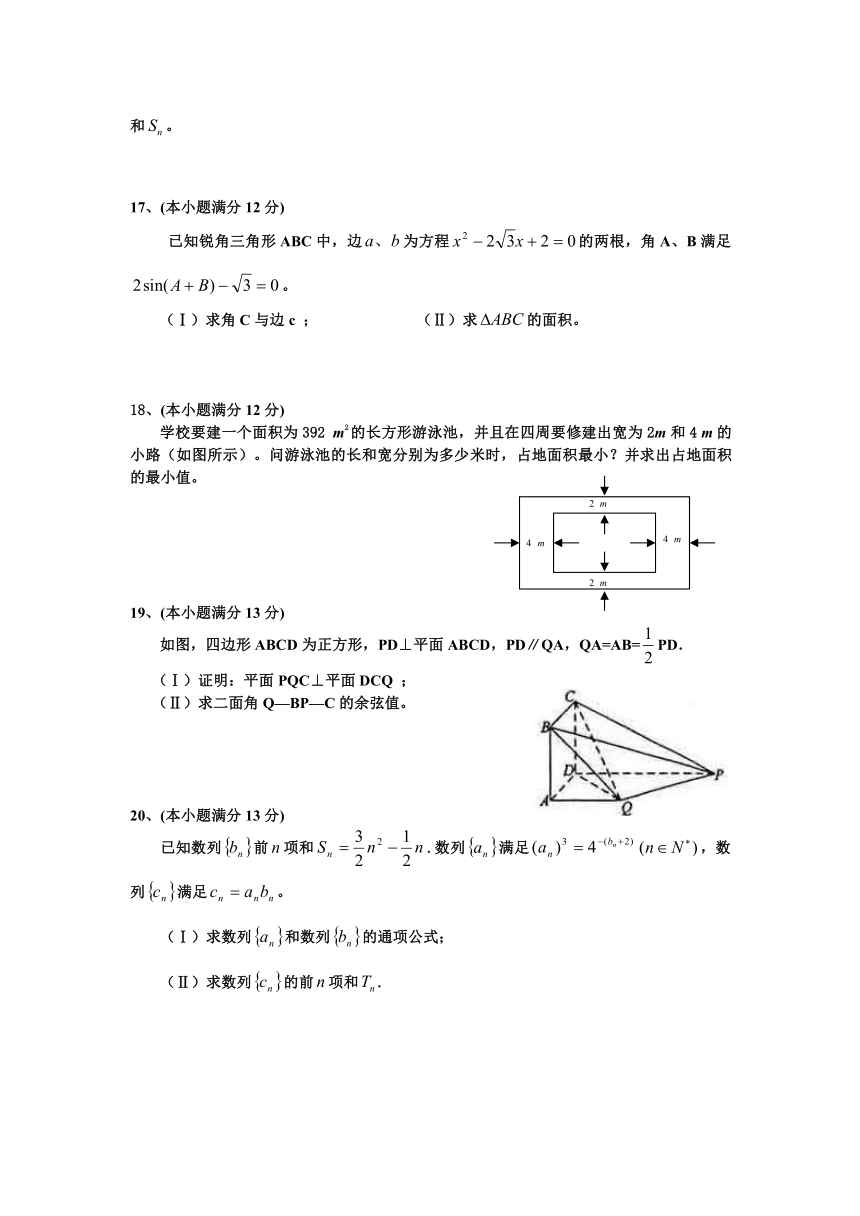
学校要建一个面积为392 m2的长方形游泳池,并且在四周要修建出宽为2m和4 m的小路(如图所示)。问游泳池的长和宽分别为多少米时,占地面积最小?并求出占地面积的最小值。
19、(本小题满分13分)
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=PD.
(Ⅰ)证明:平面PQC⊥平面DCQ ;
(Ⅱ)求二面角Q—BP—C的余弦值。
20、(本小题满分13分)
已知数列前项和.数列满足,数列满足。
(Ⅰ)求数列和数列的通项公式;
(Ⅱ)求数列的前项和.
21、(本小题满分13分)
过点的椭圆的离心率为,椭圆与 轴交于两点、,过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.
(I)求椭圆的方程
(Ⅱ)当直线l过椭圆右焦点时,求线段CD的长;
(Ⅲ)当点P异于点B时,求证:为定值.
六安市2011—2012学年第一学期期末考试
高二理科数学试卷参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C B A C D C A C
11、 -6 12、 18 13、2 14、 15、①④
16、(I) ………………………………………………………4分
(Ⅱ)……………………………………9分
数列的前项和………………12分
17、(I) ∵ ∴
由于△ABC为锐角三角形,∴C= ………………………… 3分
,得X1=, X 2=
由余弦定理,得
∴………………………………7分
(Ⅱ)S△ABC=……………………12分
18、解:设游泳池的长为x m,则游泳池的宽为m,
又设占地面积为y m2,依题意,
得=424+4(x+)≥424+224=648
当且仅当x=即 x=28时取“=”.
19、解:如图,以D为坐标原点,线段DA的长为单位长,射线DA为x轴的正半轴建立空间直角坐标系D—xyz.
(I)依题意有Q(1,1,0),C(0,0,1),P(0,2,0).
则
所以
即PQ⊥DQ,PQ⊥DC. 故PQ⊥平面DCQ.
又PQ平面PQC,所以平面PQC⊥平面DCQ. …………6分
(II)依题意有B(1,0,1),
设是平面PBC的法向量,则
因此可取
设m是平面PBQ的法向量,则
可取
故二面角Q—BP—C的余弦值为
……………………………13分
20、(Ⅰ)由已知和得,当时,
又,符合上式。故数列的通项公式。 ……………3分
又∵,∴,
故数列的通项公式为, …………………………6分
(Ⅱ),
,……………… ①
,…②
①-②得
,
∴ 。 …………………………13分
21、(Ⅰ)由已知得,解得,所以椭圆方程为.……3分
(Ⅱ)椭圆的右焦点为,此时直线的方程为 ,代入椭圆方程得
,解得,代入直线的方程得 ,
所以,
故.…………………………………………8分
(Ⅲ)当直线与轴垂直时与题意不符.
设直线的方程为.代入椭圆方程得.
解得,代入直线的方程得,
所以D点的坐标为.
又直线AC的方程为,又直线BD的方程为,
联立得
因此,又.
所以.故为定值.……………13分
高二理科数学试卷
第Ⅰ卷(共50分)
命题:余其权 审题:冯坤兵
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个备选项中,只有一项是符合题目要求的。
1、命题“”的否定为 ( )
A. B.
C. D.
2、若等差数列{}的前三项和且,则等于( )
A.4 B.5 C.6 D.7
3、若,则等于( )
A. B. C. D.
4、 在等比数列中,,则项数为( )
A.3 B.4 C.5 D.6
5、设抛物线的顶点在原点,准线方程为,则抛物线的方程是 ( )
A. B. C. D.
6、在中,,则的形状是( )
A.锐角三角形 B.直角三角形 C. 钝角三角形 D.非钝角三角形
7、已知满足约束条件 则的最大值为( )
A . B. C. D.
8、在中,一定成立的等式是( )
A. B.
C. D.
9、如图:在平行六面体中,若则下列向量中与相等的是( )
A. B.
C. D.
10、椭圆与双曲线有公共的焦点,的一条渐近线与以的长轴为直径的圆交于两点,若将线段三等分,则( )
A. B. C. D.
第Ⅱ卷(共100分)
二、填空题:本大题共5小题,每小题5分,共25分。
11、已知向量,若,则 .
12、已知且满足,则的最小值为 .
13、设双曲线的渐近线方程为,则的值为 .
14、某舰艇在A处测得遇险渔船在北偏东45°距离为10海里的C处,此时得知,该渔船沿东偏南15°方向,以每小时9海里的速度向一小岛靠近,舰艇时速21海里,则舰艇到达渔船的最短时间是 小时.
15、下列命题正确的是 .
①.命题“若,则”的逆否命题为“若,则”。
②.若为假命题,则均为假命题。
③.在中,a,b,c分别是角A,B,C对应的三边,则“是直角三角形”是“”的充要条件。
④.“”是“”的充分不必要条件。
⑤.命题“若,则”的否命题为:“若,则”.
三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.
16、(本小题满分12分)
等比数列中,已知
(Ⅰ)求数列的通项公式;
(Ⅱ)若分别为等差数列的第3项和第5项,求数列的通项公式及前项和。
17、(本小题满分12分)
已知锐角三角形ABC中,边为方程的两根,角A、B满足。
(Ⅰ)求角C与边c ; (Ⅱ)求的面积。
18、(本小题满分12分)
学校要建一个面积为392 m2的长方形游泳池,并且在四周要修建出宽为2m和4 m的小路(如图所示)。问游泳池的长和宽分别为多少米时,占地面积最小?并求出占地面积的最小值。
19、(本小题满分13分)
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=PD.
(Ⅰ)证明:平面PQC⊥平面DCQ ;
(Ⅱ)求二面角Q—BP—C的余弦值。
20、(本小题满分13分)
已知数列前项和.数列满足,数列满足。
(Ⅰ)求数列和数列的通项公式;
(Ⅱ)求数列的前项和.
21、(本小题满分13分)
过点的椭圆的离心率为,椭圆与 轴交于两点、,过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.
(I)求椭圆的方程
(Ⅱ)当直线l过椭圆右焦点时,求线段CD的长;
(Ⅲ)当点P异于点B时,求证:为定值.
六安市2011—2012学年第一学期期末考试
高二理科数学试卷参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C B A C D C A C
11、 -6 12、 18 13、2 14、 15、①④
16、(I) ………………………………………………………4分
(Ⅱ)……………………………………9分
数列的前项和………………12分
17、(I) ∵ ∴
由于△ABC为锐角三角形,∴C= ………………………… 3分
,得X1=, X 2=
由余弦定理,得
∴………………………………7分
(Ⅱ)S△ABC=……………………12分
18、解:设游泳池的长为x m,则游泳池的宽为m,
又设占地面积为y m2,依题意,
得=424+4(x+)≥424+224=648
当且仅当x=即 x=28时取“=”.
19、解:如图,以D为坐标原点,线段DA的长为单位长,射线DA为x轴的正半轴建立空间直角坐标系D—xyz.
(I)依题意有Q(1,1,0),C(0,0,1),P(0,2,0).
则
所以
即PQ⊥DQ,PQ⊥DC. 故PQ⊥平面DCQ.
又PQ平面PQC,所以平面PQC⊥平面DCQ. …………6分
(II)依题意有B(1,0,1),
设是平面PBC的法向量,则
因此可取
设m是平面PBQ的法向量,则
可取
故二面角Q—BP—C的余弦值为
……………………………13分
20、(Ⅰ)由已知和得,当时,
又,符合上式。故数列的通项公式。 ……………3分
又∵,∴,
故数列的通项公式为, …………………………6分
(Ⅱ),
,……………… ①
,…②
①-②得
,
∴ 。 …………………………13分
21、(Ⅰ)由已知得,解得,所以椭圆方程为.……3分
(Ⅱ)椭圆的右焦点为,此时直线的方程为 ,代入椭圆方程得
,解得,代入直线的方程得 ,
所以,
故.…………………………………………8分
(Ⅲ)当直线与轴垂直时与题意不符.
设直线的方程为.代入椭圆方程得.
解得,代入直线的方程得,
所以D点的坐标为.
又直线AC的方程为,又直线BD的方程为,
联立得
因此,又.
所以.故为定值.……………13分
