浙江省东阳市南马高中2012届高三下学期入学考试数学(文)试题
文档属性
| 名称 | 浙江省东阳市南马高中2012届高三下学期入学考试数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 173.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-07 15:11:27 | ||
图片预览



文档简介
选择题部分 (共50分)
参考公式:
球的表面积公式 柱体的体积公式
S=4πR2 V=Sh
球的体积公式 其中S表示柱体的底面积,h表示柱体的高
V=πR3 台体的体积公式
其中R表示球的半径 V=h(S1+ +S2)
锥体的体积公式 其中S1, S2分别表示台体的上、下底面积,
V=Sh h表示台体的高
其中S表示锥体的底面积,h表示锥体的高 如果事件A,B互斥,那么
P(A+B)=P(A)+P(B)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
(1) 若全集U={-1,0,1,2},P={x∈Z | x2<2},则 U P=
(A) {2} (B) {0,2} (C) {-1,2} (D) {-1,0,2}
(2) 已知i为虚数单位,则=
(A) (B) (C) (D)
(3) 在△ABC中,“A=60°”是“cos A=”的
(A) 充分而不必要条件 (B) 必要而不充分条件
(C) 充分必要条件 (D) 既不充分也不必要条件
(4) 函数f (x)=ex+3x的零点个数是
(A) 0 (B) 1 (C) 2 (D) 3
(5) 已知直线l∥平面α,P∈α,那么过点P且平行于直线l的直线
(A) 只有一条,不在平面α内
(B) 有无数条,不一定在平面α内
(C) 只有一条,且在平面α内
(D) 有无数条,一定在平面α内
(6) 若某几何体的三视图 (单位:cm) 如图所示,则此几何体的体积是
(A) 36 cm3 (B) 48 cm3
(C) 60 cm3 (D) 72 cm3
(7) 若有2位老师,2位学生站成一排合影,则每位老师都不站在两端的概率是
(A) (B) (C) (D)
(8) 在△ABC中,角A,B,C所对的边分别为a,b,c.若
sin2 B+sin2 C-sin2A+sin B sin C=0,则tan A的值是
(A) (B) - (C) (D) -
(9) 如图,有4个半径都为1的圆,其圆心分别为O1(0,0),O2(2,0), O3(0,2),O4(2,2).记集合M={⊙Oi|i=1,2,3,4}.若A,B为M的非空子集,且A中的任何一个圆与B中的任何一个圆均无公共点,则称 (A,B) 为一个“有序集合对” (当A≠B时,(A,B) 和 (B,A) 为不同的有序集合对),那么M中“有序集合对” (A,B) 的个数是
(A) 2 (B) 4 (C) 6 (D) 8
(10) 已知点P在曲线C1:上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则 | PQ |-| PR | 的最大值是
(A) 6 (B) 8 (C) 10 (D) 12
非选择题部分 (共100分)
二、填空题:本大题共7小题,每小题4分,共28分。
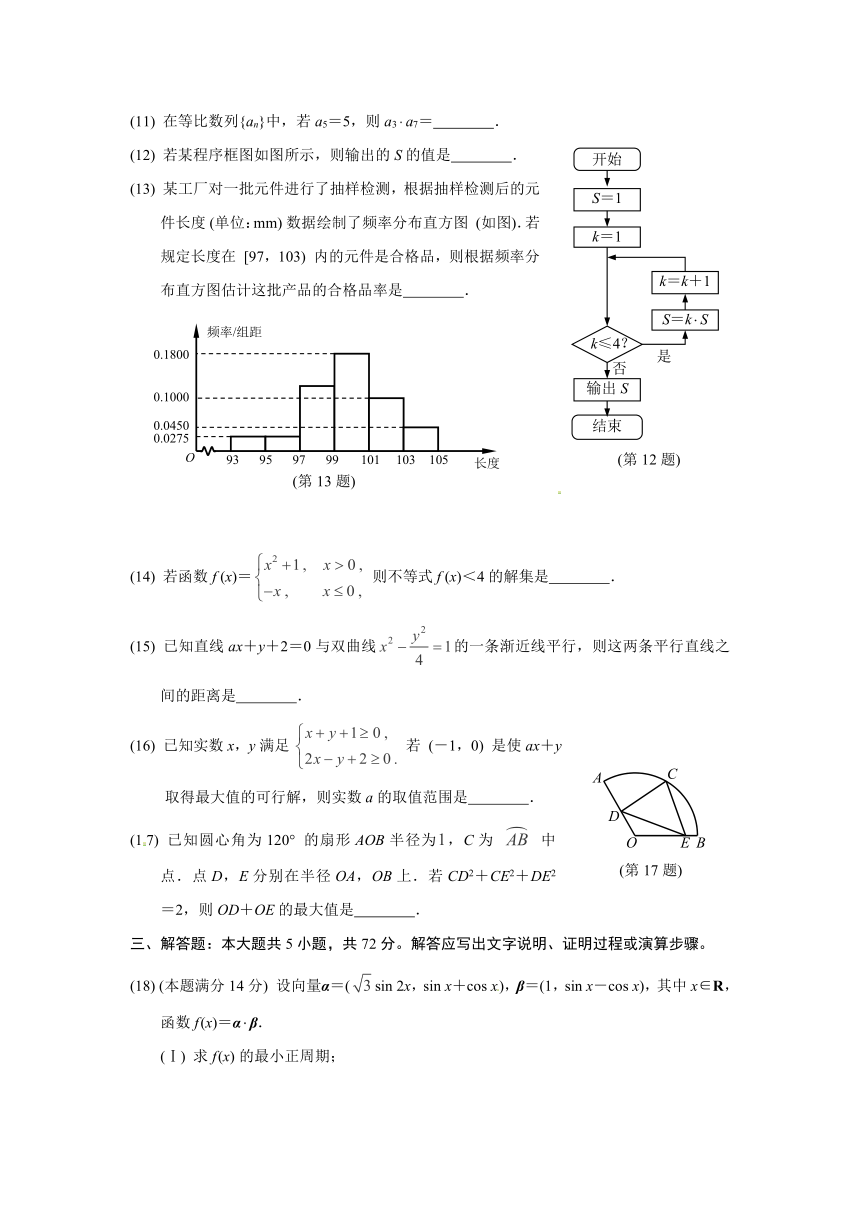
(11) 在等比数列{an}中,若a5=5,则a3a7= .
(12) 若某程序框图如图所示,则输出的S的值是 .
(13) 某工厂对一批元件进行了抽样检测,根据抽样检测后的元件长度 (单位:mm) 数据绘制了频率分布直方图 (如图).若规定长度在 [97,103) 内的元件是合格品,则根据频率分布直方图估计这批产品的合格品率是 .
(14) 若函数f (x)= 则不等式f (x)<4的解集是 .
(15) 已知直线ax+y+2=0与双曲线的一条渐近线平行,则这两条平行直线之间的距离是 .
(16) 已知实数x,y满足若 (-1,0) 是使ax+y取得最大值的可行解,则实数a的取值范围是 .
(17) 已知圆心角为120° 的扇形AOB半径为,C为 中点.点D,E分别在半径OA,OB上.若CD2+CE2+DE2=2,则OD+OE的最大值是 .
三、解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
(18) (本题满分14分) 设向量α=(sin 2x,sin x+cos x),β=(1,sin x-cos x),其中x∈R,函数f (x)=αβ.
(Ⅰ) 求f (x) 的最小正周期;
(Ⅱ) 若f (θ)=,其中0<θ<,求cos(θ+)的值.
(19) (本题满分14分) 设等差数列{an}的首项a1为a,公差d=2,前n项和为Sn.
(Ⅰ) 若S1,S2,S4成等比数列,求数列{an}的通项公式;
(Ⅱ) 证明:n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
(20) (本题满分14分) 已知正四棱锥P-ABCD中,底面是边长为2 的正方形,高为.M为线段PC的中点.
(Ⅰ) 求证:PA∥平面MDB;
(Ⅱ) N为AP的中点,求CN与平面MBD所成角的正切值.
(21) (本题满分15分) 已知函数f (x)=x3+ax2+bx, a , bR.
(Ⅰ) 曲线C:y=f (x) 经过点P (1,2),且曲线C在点P处的切线平行于直线y=2x+1,求a,b的值;
(Ⅱ) 已知f (x)在区间 (1 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ),2) 内存在两个极值点,求证:0<a+b<2.
(22) (本题满分15分) 设抛物线C1:x 2=4 y的焦点为F,曲线C2与C1关于原点对称.
(Ⅰ) 求曲线C2的方程;
(Ⅱ) 曲线C2上是否存在一点P(异于原点),过点P作C1的两条切线PA,PB,切点A,B,满足| AB |是 | FA | 与 | FB | 的等差中项?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案
一、选择题: 本题考查基本知识和基本运算。每小题5分, 满分50分。
二、填空题:本题考查基本知识和基本运算。每小题4分,满分28分。
三、解答题:本大题共5小题,共72分。
(18) 本题主要考查三角函数性质与三角恒等变换、三角计算等基础知识,同时考查平面向量应用及三角运算求解能力。满分14分。
(Ⅰ)解:由题意得 f (x)=sin 2x+(sin x-cos x)(sin x+cos x)
=sin 2x-cos 2x=2sin (2x-),
故 f (x)的最小正周期T==π. …………6分
(Ⅱ)解:若f (θ)=,则2sin (2θ-)=,
所以,sin (2θ-)=.
又因为0<θ<,所以θ=或.
当θ=时,cos(θ+)=cos(+)=;
当θ=时,cos(θ+)=cos(+)=-cos=-. ………14分
(19) 本题主要考查等差数列、等比数列概念、求和公式等基础知识,同时考查推理论证能力及分析问题解决问题的能力。满分14分。
(Ⅰ)解:因为Sn=na+n (n-1),
S1=a,S2=2a+2,S4=4a+12.由于S1,S2,S4成等比数列,因此
=S1S4,即得a=1.an=2n-1. …………6分
(Ⅱ)证明:采用反证法.不失一般性,不妨设对某个m∈N*,Sm,Sm+1,Sm+2构成等比数列,即.因此
a2+2ma+2m(m+1)=0,
要使数列{an}的首项a存在,上式中的Δ≥0.然而
Δ=(2m)2-8m(m+1)=-4m (2+m)<0,矛盾.
所以,对任意正整数n,Sn,Sn+1,Sn+2都不构成等比数列. …………14分
(20) 本题主要考查空间点、线、面位置关系,线面角等基础知识,同时考查空间想象能力和推理论证能力。满分14分。
(Ⅰ)证明:在四棱锥P-ABCD中,连结AC交BD于点O,连结OM,PO.由条件可得PO=,AC=2,PA=PC=2,CO=AO=.
因为在△PAC中,M为PC的中点,O为AC的中点,
所以OM为△PAC的中位线,得OM∥AP,
又因为AP平面MDB,OM平面MDB,
所以PA∥平面MDB. …………6分
(21) 本题主要考查函数的极值概念、导数运算法则、导数应用及二次方程根的分布等基础知识,同时考查抽象概括能力和推理论证能力。满分15分。
(Ⅰ)解:
=,
由题设知: 解得 …………6分
(Ⅱ)解:因为在区间内存在两个极值点 ,
所以,即在内有两个不等的实根.
故
由 (1)+(3)得.
由(4)得,
因,故,从而.
所以. …………15分
(Ⅰ)解;因为曲线与关于原点对称,又的方程,
所以方程为. …………5分
(Ⅱ)解:设,,,.
的导数为,则切线的方程,
又,得,
因点在切线上,故.
同理, .
所以直线经过两点,
即直线方程为,即,
代入得,则,,
所以 ,
由抛物线定义得,.
…………15分
2
4
2
2
2
2
正视图
(第6题)
侧视图
俯视图
x
O1
O2
O3
O4
y
(第10题)
S=1
开始
k=1
k≤4?
输出S
结束
k=k+1
S=kS
是
否
(第12题)
频率/组距
0.1800
0.1000
0.0450
0.0275
O
95
93
99
97
103
101
105
长度
(第13题)
A
B
O
E
D
C
(第17题)
A
B
D
C
M
P
N
(第20题)
F
x
y
O
(第22题)
A
B
D
C
M
P
N
(第20题)
O
E
参考公式:
球的表面积公式 柱体的体积公式
S=4πR2 V=Sh
球的体积公式 其中S表示柱体的底面积,h表示柱体的高
V=πR3 台体的体积公式
其中R表示球的半径 V=h(S1+ +S2)
锥体的体积公式 其中S1, S2分别表示台体的上、下底面积,
V=Sh h表示台体的高
其中S表示锥体的底面积,h表示锥体的高 如果事件A,B互斥,那么
P(A+B)=P(A)+P(B)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
(1) 若全集U={-1,0,1,2},P={x∈Z | x2<2},则 U P=
(A) {2} (B) {0,2} (C) {-1,2} (D) {-1,0,2}
(2) 已知i为虚数单位,则=
(A) (B) (C) (D)
(3) 在△ABC中,“A=60°”是“cos A=”的
(A) 充分而不必要条件 (B) 必要而不充分条件
(C) 充分必要条件 (D) 既不充分也不必要条件
(4) 函数f (x)=ex+3x的零点个数是
(A) 0 (B) 1 (C) 2 (D) 3
(5) 已知直线l∥平面α,P∈α,那么过点P且平行于直线l的直线
(A) 只有一条,不在平面α内
(B) 有无数条,不一定在平面α内
(C) 只有一条,且在平面α内
(D) 有无数条,一定在平面α内
(6) 若某几何体的三视图 (单位:cm) 如图所示,则此几何体的体积是
(A) 36 cm3 (B) 48 cm3
(C) 60 cm3 (D) 72 cm3
(7) 若有2位老师,2位学生站成一排合影,则每位老师都不站在两端的概率是
(A) (B) (C) (D)
(8) 在△ABC中,角A,B,C所对的边分别为a,b,c.若
sin2 B+sin2 C-sin2A+sin B sin C=0,则tan A的值是
(A) (B) - (C) (D) -
(9) 如图,有4个半径都为1的圆,其圆心分别为O1(0,0),O2(2,0), O3(0,2),O4(2,2).记集合M={⊙Oi|i=1,2,3,4}.若A,B为M的非空子集,且A中的任何一个圆与B中的任何一个圆均无公共点,则称 (A,B) 为一个“有序集合对” (当A≠B时,(A,B) 和 (B,A) 为不同的有序集合对),那么M中“有序集合对” (A,B) 的个数是
(A) 2 (B) 4 (C) 6 (D) 8
(10) 已知点P在曲线C1:上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则 | PQ |-| PR | 的最大值是
(A) 6 (B) 8 (C) 10 (D) 12
非选择题部分 (共100分)
二、填空题:本大题共7小题,每小题4分,共28分。
(11) 在等比数列{an}中,若a5=5,则a3a7= .
(12) 若某程序框图如图所示,则输出的S的值是 .
(13) 某工厂对一批元件进行了抽样检测,根据抽样检测后的元件长度 (单位:mm) 数据绘制了频率分布直方图 (如图).若规定长度在 [97,103) 内的元件是合格品,则根据频率分布直方图估计这批产品的合格品率是 .
(14) 若函数f (x)= 则不等式f (x)<4的解集是 .
(15) 已知直线ax+y+2=0与双曲线的一条渐近线平行,则这两条平行直线之间的距离是 .
(16) 已知实数x,y满足若 (-1,0) 是使ax+y取得最大值的可行解,则实数a的取值范围是 .
(17) 已知圆心角为120° 的扇形AOB半径为,C为 中点.点D,E分别在半径OA,OB上.若CD2+CE2+DE2=2,则OD+OE的最大值是 .
三、解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
(18) (本题满分14分) 设向量α=(sin 2x,sin x+cos x),β=(1,sin x-cos x),其中x∈R,函数f (x)=αβ.
(Ⅰ) 求f (x) 的最小正周期;
(Ⅱ) 若f (θ)=,其中0<θ<,求cos(θ+)的值.
(19) (本题满分14分) 设等差数列{an}的首项a1为a,公差d=2,前n项和为Sn.
(Ⅰ) 若S1,S2,S4成等比数列,求数列{an}的通项公式;
(Ⅱ) 证明:n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
(20) (本题满分14分) 已知正四棱锥P-ABCD中,底面是边长为2 的正方形,高为.M为线段PC的中点.
(Ⅰ) 求证:PA∥平面MDB;
(Ⅱ) N为AP的中点,求CN与平面MBD所成角的正切值.
(21) (本题满分15分) 已知函数f (x)=x3+ax2+bx, a , bR.
(Ⅰ) 曲线C:y=f (x) 经过点P (1,2),且曲线C在点P处的切线平行于直线y=2x+1,求a,b的值;
(Ⅱ) 已知f (x)在区间 (1 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ),2) 内存在两个极值点,求证:0<a+b<2.
(22) (本题满分15分) 设抛物线C1:x 2=4 y的焦点为F,曲线C2与C1关于原点对称.
(Ⅰ) 求曲线C2的方程;
(Ⅱ) 曲线C2上是否存在一点P(异于原点),过点P作C1的两条切线PA,PB,切点A,B,满足| AB |是 | FA | 与 | FB | 的等差中项?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案
一、选择题: 本题考查基本知识和基本运算。每小题5分, 满分50分。
二、填空题:本题考查基本知识和基本运算。每小题4分,满分28分。
三、解答题:本大题共5小题,共72分。
(18) 本题主要考查三角函数性质与三角恒等变换、三角计算等基础知识,同时考查平面向量应用及三角运算求解能力。满分14分。
(Ⅰ)解:由题意得 f (x)=sin 2x+(sin x-cos x)(sin x+cos x)
=sin 2x-cos 2x=2sin (2x-),
故 f (x)的最小正周期T==π. …………6分
(Ⅱ)解:若f (θ)=,则2sin (2θ-)=,
所以,sin (2θ-)=.
又因为0<θ<,所以θ=或.
当θ=时,cos(θ+)=cos(+)=;
当θ=时,cos(θ+)=cos(+)=-cos=-. ………14分
(19) 本题主要考查等差数列、等比数列概念、求和公式等基础知识,同时考查推理论证能力及分析问题解决问题的能力。满分14分。
(Ⅰ)解:因为Sn=na+n (n-1),
S1=a,S2=2a+2,S4=4a+12.由于S1,S2,S4成等比数列,因此
=S1S4,即得a=1.an=2n-1. …………6分
(Ⅱ)证明:采用反证法.不失一般性,不妨设对某个m∈N*,Sm,Sm+1,Sm+2构成等比数列,即.因此
a2+2ma+2m(m+1)=0,
要使数列{an}的首项a存在,上式中的Δ≥0.然而
Δ=(2m)2-8m(m+1)=-4m (2+m)<0,矛盾.
所以,对任意正整数n,Sn,Sn+1,Sn+2都不构成等比数列. …………14分
(20) 本题主要考查空间点、线、面位置关系,线面角等基础知识,同时考查空间想象能力和推理论证能力。满分14分。
(Ⅰ)证明:在四棱锥P-ABCD中,连结AC交BD于点O,连结OM,PO.由条件可得PO=,AC=2,PA=PC=2,CO=AO=.
因为在△PAC中,M为PC的中点,O为AC的中点,
所以OM为△PAC的中位线,得OM∥AP,
又因为AP平面MDB,OM平面MDB,
所以PA∥平面MDB. …………6分
(21) 本题主要考查函数的极值概念、导数运算法则、导数应用及二次方程根的分布等基础知识,同时考查抽象概括能力和推理论证能力。满分15分。
(Ⅰ)解:
=,
由题设知: 解得 …………6分
(Ⅱ)解:因为在区间内存在两个极值点 ,
所以,即在内有两个不等的实根.
故
由 (1)+(3)得.
由(4)得,
因,故,从而.
所以. …………15分
(Ⅰ)解;因为曲线与关于原点对称,又的方程,
所以方程为. …………5分
(Ⅱ)解:设,,,.
的导数为,则切线的方程,
又,得,
因点在切线上,故.
同理, .
所以直线经过两点,
即直线方程为,即,
代入得,则,,
所以 ,
由抛物线定义得,.
…………15分
2
4
2
2
2
2
正视图
(第6题)
侧视图
俯视图
x
O1
O2
O3
O4
y
(第10题)
S=1
开始
k=1
k≤4?
输出S
结束
k=k+1
S=kS
是
否
(第12题)
频率/组距
0.1800
0.1000
0.0450
0.0275
O
95
93
99
97
103
101
105
长度
(第13题)
A
B
O
E
D
C
(第17题)
A
B
D
C
M
P
N
(第20题)
F
x
y
O
(第22题)
A
B
D
C
M
P
N
(第20题)
O
E
同课章节目录
