2020—2021学年北师大版八年级数学下册2.6《 一元一次不等式组》课件(共26张ppt)
文档属性
| 名称 | 2020—2021学年北师大版八年级数学下册2.6《 一元一次不等式组》课件(共26张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-30 20:23:52 | ||
图片预览



文档简介
北师大版八年级数学下册
2.6
一元一次不等式组
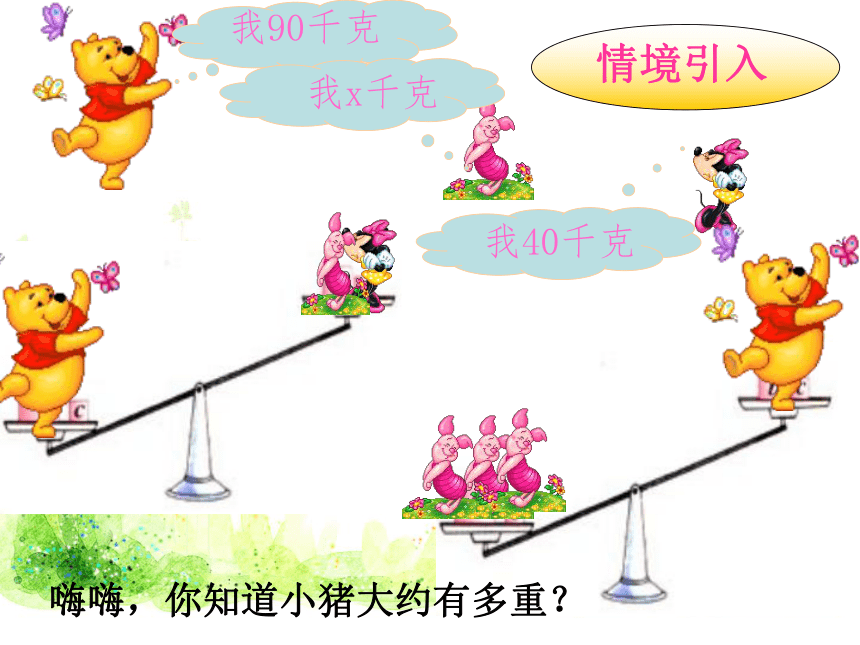
情境引入
我90千克
我x千克
我40千克
嗨嗨,你知道小猪大约有多重?
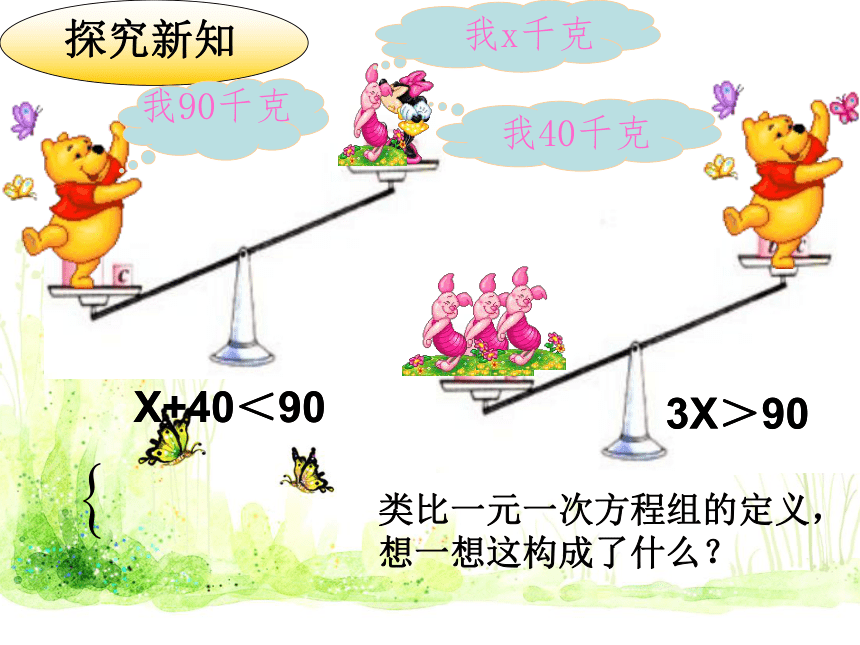
探究新知
我90千克
我x千克
我40千克
X+40<90
3X>90
X+40<90
3X>90
类比一元一次方程组的定义,想一想这构成了什么?
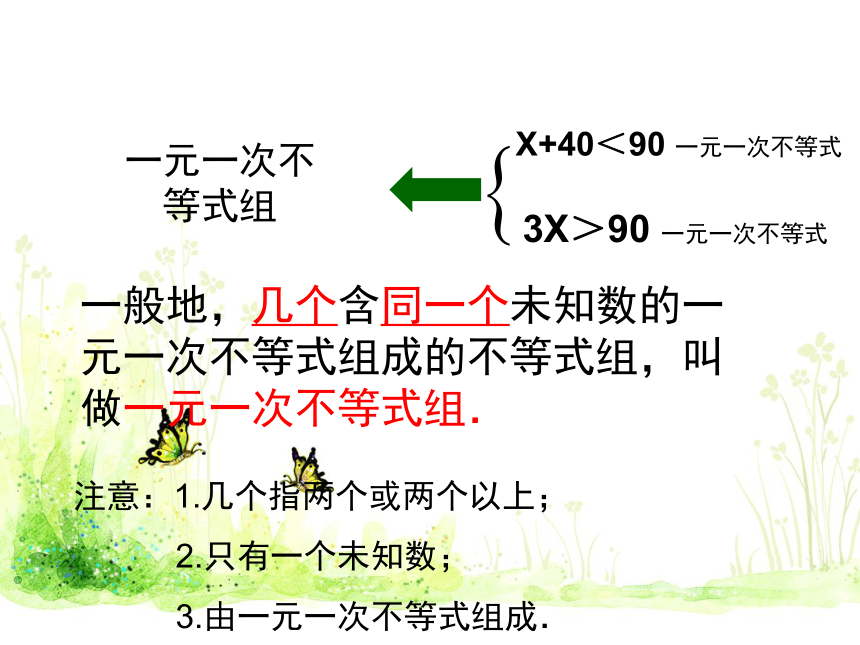
X+40<90 一元一次不等式
3X>90 一元一次不等式
一元一次不等式组
一般地,几个含同一个未知数的一元一次不等式组成的不等式组,叫做一元一次不等式组.
注意:1.几个指两个或两个以上;
2.只有一个未知数;
3.由一元一次不等式组成.
下列各式哪些是一元一次不等式组,哪些不是为什么?
(1)
(2)
(3)
4(x+5) >100
4(y-5)<68
3x-5>5x+1
是
不是
不是
是
不是
是
考考你
是
考考你
不是
不是
下列各式哪些是一元一次不等式组,哪些不是为什么?
②
①
动手操作:
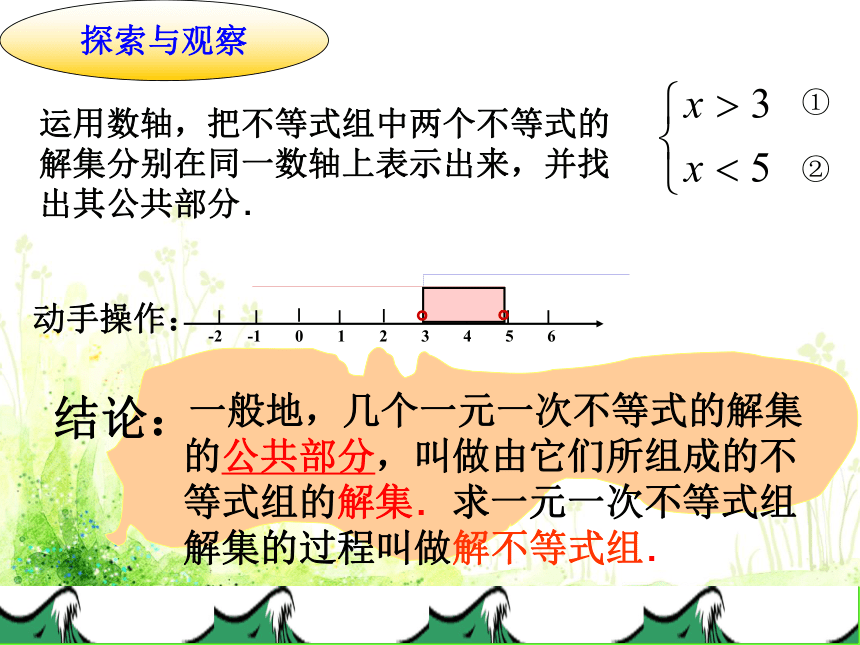
探索与观察
-2 -1 0 1 2 3 4 5 6
一般地,几个一元一次不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.求一元一次不等式组解集的过程叫做解不等式组.
运用数轴,把不等式组中两个不等式的解集分别在同一数轴上表示出来,并找出其公共部分.
结论:
。
。
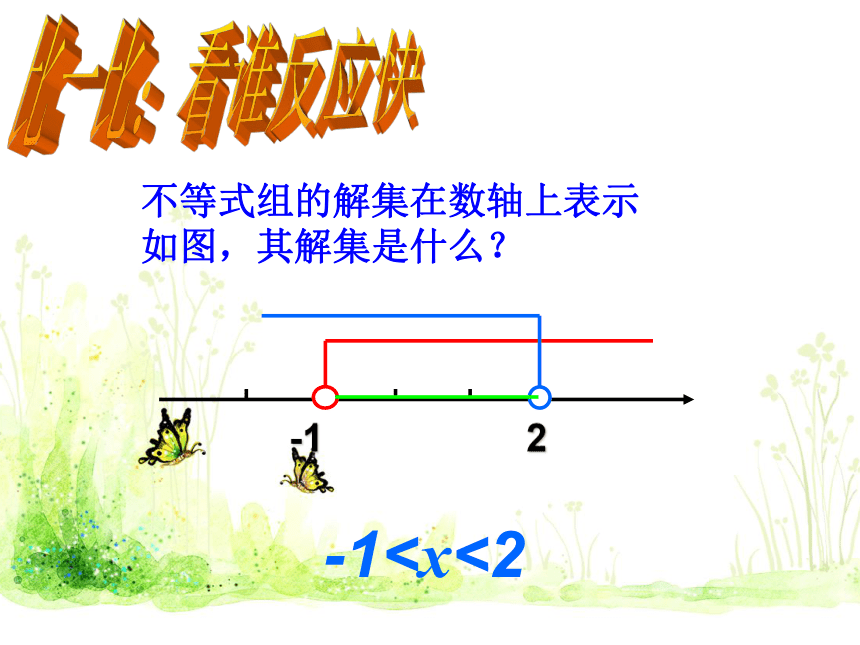
-1 2
不等式组的解集在数轴上表示如图,其解集是什么?
-1比一比:看谁反应快
–2 –1 0 1 2
比一比:看谁反应快
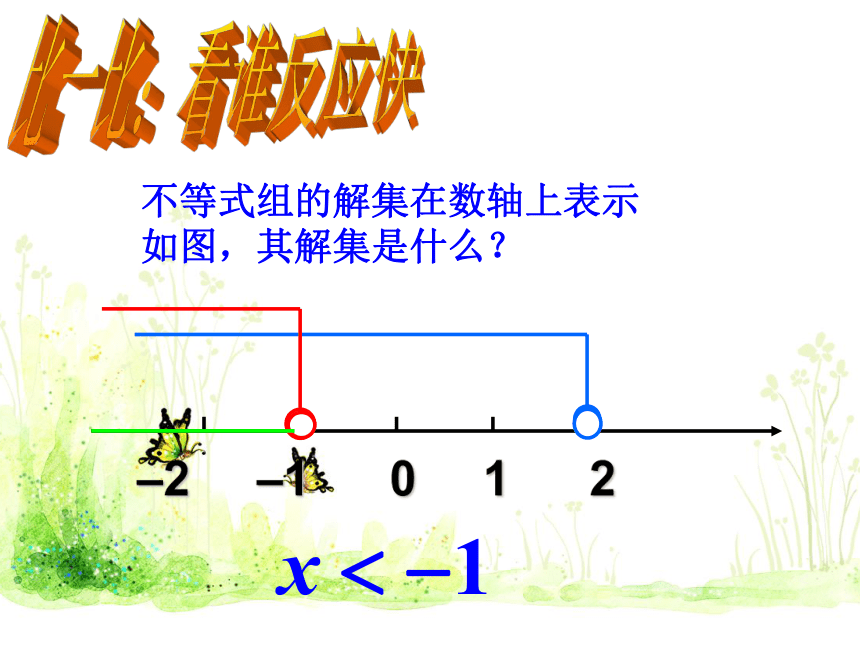
不等式组的解集在数轴上表示如图,其解集是什么?
–2 –1 0 1 2
不等式组无解
比一比:看谁反应快
不等式组的解集在数轴上表示如图,其解集是什么?
–2 –1 0 1 2
比一比:看谁反应快
不等式组的解集在数轴上表示如图,其解集是什么?
例1 解不等式组
解:
解不等式①得:
解不等式②得:
所以不等式组的解集为:
解不等式③得:
例2
2
0
4
1
3
由数轴图可以发现:
解得:
所以
符合条件的整数的值为
24.25.26.27.28.29.30.
例3一次野营活动,小明把自己带来的若干个苹果分给班上若干个同学,如果每人分4个苹果那么还剩下20个苹果,如果每人分8个苹果,那么最后一个同学分得的不足8个苹果,求苹果的总个数.
解:设共有x名同学,
苹果有(4x+20)个.
列不等式组:
解不等式①得:
解不等式②得:
不等式组解集为:
答:共有6名同学,44个苹果.
我90千克
我x千克
我40千克
X+40<90
3X>90
X+40<90
3X>90
3x>90
x+40<90
①
②
由①解得:x<50
由②解得:x>30
在数轴上表示不等式①,②的解集
0
50
30
∴这个不等式组的解集是:30解:
答:小猪的体重大约30至50千克.
-5
-2
0
-3
-1
-4
◆ 求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
-5
-2
0
-3
-1
2
1
-4
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
大大取大
-5
-2
0
-3
-1
1
-4
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
-3
-1
-4
0
-7
-6
◆求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
小小取小
-5
-2
0
-3
-1
1
-4
-6
-5
-2
-3
-1
-4
0
-7
-6
◆求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
大小小大中间找
◆求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-5
-2
-3
-1
-4
0
-7
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
0
-3
-1
1
-4
-6
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
大大小小解不了
2x-1>x-2
x+8>4x-1
例:
解下列不等式组,并在数轴上表示出解集.
①
②
解:解不等式①,得 x>﹣1.
解不等式② ,得 x<3.
在数轴上表示不等式①, ②的解集
-1
3
所以这个不等式组的解集是 ﹣1知识应用
练习:解不等式组
小结
1.数形结合法,依靠数轴求不等式组的解集.
2.会运用不等式组的知识解决实际问题,并注意检验结果的合理性.
2.6
一元一次不等式组
情境引入
我90千克
我x千克
我40千克
嗨嗨,你知道小猪大约有多重?
探究新知
我90千克
我x千克
我40千克
X+40<90
3X>90
X+40<90
3X>90
类比一元一次方程组的定义,想一想这构成了什么?
X+40<90 一元一次不等式
3X>90 一元一次不等式
一元一次不等式组
一般地,几个含同一个未知数的一元一次不等式组成的不等式组,叫做一元一次不等式组.
注意:1.几个指两个或两个以上;
2.只有一个未知数;
3.由一元一次不等式组成.
下列各式哪些是一元一次不等式组,哪些不是为什么?
(1)
(2)
(3)
4(x+5) >100
4(y-5)<68
3x-5>5x+1
是
不是
不是
是
不是
是
考考你
是
考考你
不是
不是
下列各式哪些是一元一次不等式组,哪些不是为什么?
②
①
动手操作:
探索与观察
-2 -1 0 1 2 3 4 5 6
一般地,几个一元一次不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.求一元一次不等式组解集的过程叫做解不等式组.
运用数轴,把不等式组中两个不等式的解集分别在同一数轴上表示出来,并找出其公共部分.
结论:
。
。
-1 2
不等式组的解集在数轴上表示如图,其解集是什么?
-1
–2 –1 0 1 2
比一比:看谁反应快
不等式组的解集在数轴上表示如图,其解集是什么?
–2 –1 0 1 2
不等式组无解
比一比:看谁反应快
不等式组的解集在数轴上表示如图,其解集是什么?
–2 –1 0 1 2
比一比:看谁反应快
不等式组的解集在数轴上表示如图,其解集是什么?
例1 解不等式组
解:
解不等式①得:
解不等式②得:
所以不等式组的解集为:
解不等式③得:
例2
2
0
4
1
3
由数轴图可以发现:
解得:
所以
符合条件的整数的值为
24.25.26.27.28.29.30.
例3一次野营活动,小明把自己带来的若干个苹果分给班上若干个同学,如果每人分4个苹果那么还剩下20个苹果,如果每人分8个苹果,那么最后一个同学分得的不足8个苹果,求苹果的总个数.
解:设共有x名同学,
苹果有(4x+20)个.
列不等式组:
解不等式①得:
解不等式②得:
不等式组解集为:
答:共有6名同学,44个苹果.
我90千克
我x千克
我40千克
X+40<90
3X>90
X+40<90
3X>90
3x>90
x+40<90
①
②
由①解得:x<50
由②解得:x>30
在数轴上表示不等式①,②的解集
0
50
30
∴这个不等式组的解集是:30
答:小猪的体重大约30至50千克.
-5
-2
0
-3
-1
-4
◆ 求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
-5
-2
0
-3
-1
2
1
-4
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
大大取大
-5
-2
0
-3
-1
1
-4
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
-3
-1
-4
0
-7
-6
◆求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
小小取小
-5
-2
0
-3
-1
1
-4
-6
-5
-2
-3
-1
-4
0
-7
-6
◆求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
大小小大中间找
◆求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-5
-2
-3
-1
-4
0
-7
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
0
-3
-1
1
-4
-6
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
大大小小解不了
2x-1>x-2
x+8>4x-1
例:
解下列不等式组,并在数轴上表示出解集.
①
②
解:解不等式①,得 x>﹣1.
解不等式② ,得 x<3.
在数轴上表示不等式①, ②的解集
-1
3
所以这个不等式组的解集是 ﹣1
练习:解不等式组
小结
1.数形结合法,依靠数轴求不等式组的解集.
2.会运用不等式组的知识解决实际问题,并注意检验结果的合理性.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
