2020-2021学年鲁教版(五四制)八年级下册数学 8.6一元二次方程的应用(3)销售利润问题 课件(共14张ppt)
文档属性
| 名称 | 2020-2021学年鲁教版(五四制)八年级下册数学 8.6一元二次方程的应用(3)销售利润问题 课件(共14张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 480.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-30 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
8.6一元二次方程的应用
销售利润问题
鲁教版八年级下册
1.会找商品销售问题中的等量关系。
2.会用一元二次方程按步骤解决有关销售利润问题。
3.以一元一次方程解决的实际问题为载体,使学生初步掌握数学建模的基本方法。
学习目标
小明在花店共卖出200支玫瑰,每支的进价为6元,售价为10元
(1)每支的利润是多少元?
(2)总利润是多少元;
(10-6)x
200=800(元)
单件利润×销售量=总利润
等量关系:
情景创设
等量
关系
促销活动:
销售价每支降低2元,多卖出100件。
情景创设
1、降价后,你们发现了什么?
2、售价的变化,引起了哪些量的变化?
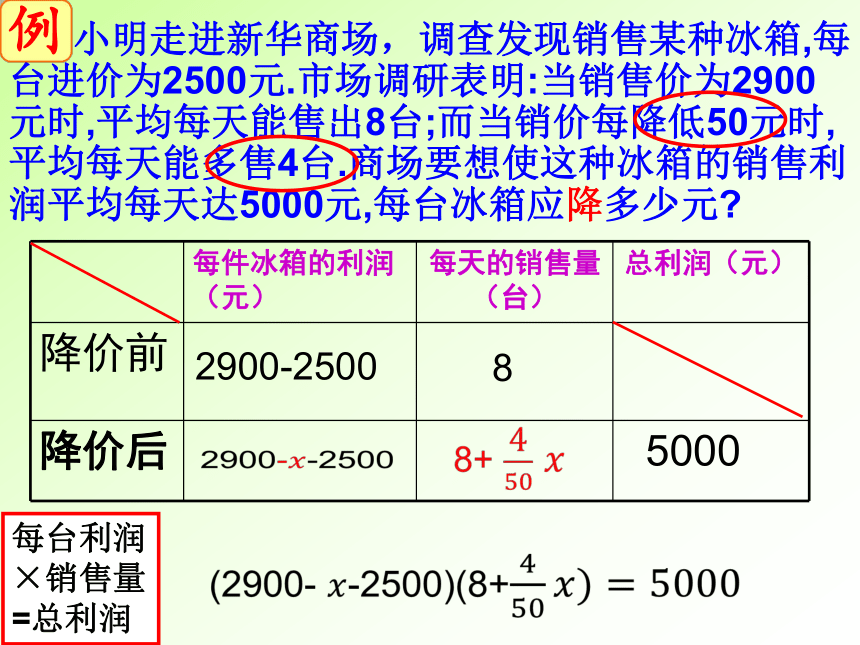
小明走进新华商场,调查发现销售某种冰箱,每台进价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润平均每天达5000元,每台冰箱应降多少元?
每台利润×销售量=总利润
?
例
每件冰箱的利润(元)
每天的销售量(台)
总利润(元)
降价前
降价后
5000
?
8
2900-2500
?
例
新华商场销售某种冰箱,每台进价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱应降多少元?
的定价为多少元
?
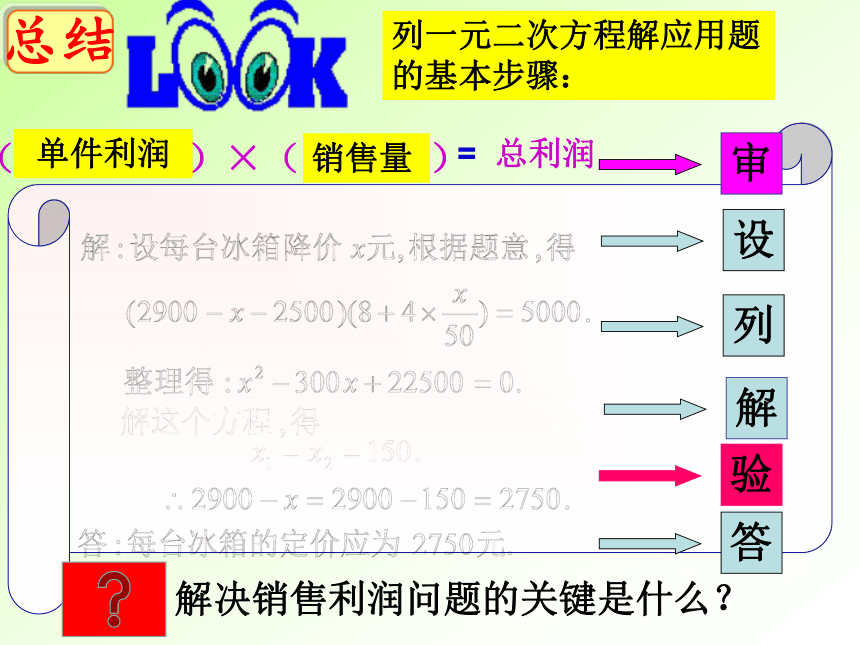
列一元二次方程解应用题的基本步骤:
(
)×(
)
单件利润
销售量
=
总利润
答
设
列
解
验
审
解决销售利润问题的关键是什么?
总结
对应练习
某种服装,平均每天可销售20件,每件盈利44元.若每件降价10元,则每天可多售50件.如果每天盈利1600元,应降多少元?(只列方程)
小试牛刀
(44-x)
(
)=1600
?
某商场将进货价为30元的台灯以40元售出,平均每月能售出600个.市场调研表明:当销售价为每上涨1元时,其销售量就将减少10个.商场要想销售利润平均每月达到10000元,同时也让顾客获得最大的实惠,每个台灯的定价应为多少元?
定价为40+10=50(元)
?
?
启发引导
通过这节课的学习活动你有哪些收获?
你还有什么疑惑吗?
总结反思
送你一句话共勉
学无止境,迎难而上
......
相信同学们都会成为数学高手.
中考链接
(2012山西)山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,为尽快减少库存,商场决定采取适当的措施,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若每天该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)该店应按原售价的几折出售?
拓展延伸
拓展延伸:中考链接
(1)每千克核桃应降价多少元?
解:⑴设每千克核桃应降价x元
?
∴
x2-10x+24=0
解得:x1=4,
x2=6
答:每千克核桃应降价6元
因为要尽快减少库存
?
拓展延伸:中考链接
(2)该店应按原售价的几折出售?
解:由(1)可知每千克核桃可6元。
此时,售价:60-6=54(元),
答:该店应按原售价的9折出售
?
8.6一元二次方程的应用
销售利润问题
鲁教版八年级下册
1.会找商品销售问题中的等量关系。
2.会用一元二次方程按步骤解决有关销售利润问题。
3.以一元一次方程解决的实际问题为载体,使学生初步掌握数学建模的基本方法。
学习目标
小明在花店共卖出200支玫瑰,每支的进价为6元,售价为10元
(1)每支的利润是多少元?
(2)总利润是多少元;
(10-6)x
200=800(元)
单件利润×销售量=总利润
等量关系:
情景创设
等量
关系
促销活动:
销售价每支降低2元,多卖出100件。
情景创设
1、降价后,你们发现了什么?
2、售价的变化,引起了哪些量的变化?
小明走进新华商场,调查发现销售某种冰箱,每台进价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润平均每天达5000元,每台冰箱应降多少元?
每台利润×销售量=总利润
?
例
每件冰箱的利润(元)
每天的销售量(台)
总利润(元)
降价前
降价后
5000
?
8
2900-2500
?
例
新华商场销售某种冰箱,每台进价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱应降多少元?
的定价为多少元
?
列一元二次方程解应用题的基本步骤:
(
)×(
)
单件利润
销售量
=
总利润
答
设
列
解
验
审
解决销售利润问题的关键是什么?
总结
对应练习
某种服装,平均每天可销售20件,每件盈利44元.若每件降价10元,则每天可多售50件.如果每天盈利1600元,应降多少元?(只列方程)
小试牛刀
(44-x)
(
)=1600
?
某商场将进货价为30元的台灯以40元售出,平均每月能售出600个.市场调研表明:当销售价为每上涨1元时,其销售量就将减少10个.商场要想销售利润平均每月达到10000元,同时也让顾客获得最大的实惠,每个台灯的定价应为多少元?
定价为40+10=50(元)
?
?
启发引导
通过这节课的学习活动你有哪些收获?
你还有什么疑惑吗?
总结反思
送你一句话共勉
学无止境,迎难而上
......
相信同学们都会成为数学高手.
中考链接
(2012山西)山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,为尽快减少库存,商场决定采取适当的措施,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若每天该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)该店应按原售价的几折出售?
拓展延伸
拓展延伸:中考链接
(1)每千克核桃应降价多少元?
解:⑴设每千克核桃应降价x元
?
∴
x2-10x+24=0
解得:x1=4,
x2=6
答:每千克核桃应降价6元
因为要尽快减少库存
?
拓展延伸:中考链接
(2)该店应按原售价的几折出售?
解:由(1)可知每千克核桃可6元。
此时,售价:60-6=54(元),
答:该店应按原售价的9折出售
?
