18.2勾股定理的逆定理 测试(1)(有答案)
文档属性
| 名称 | 18.2勾股定理的逆定理 测试(1)(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 47.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-07 17:18:43 | ||
图片预览

文档简介
18.2勾股定理的逆定理 测试(1)
1、小红要求△ABC最长边上的高,测得AB=8 cm,AC=6 cm,BC=10 cm,则可知最长边上的高是( )
A.48 cm B.4.8 cm
C.0.48 cm D.5 cm
2、已知a,b,c为△ABC三边,且满足a2c2-b2c2=a4-b4,则它的形状为( )
A.直角三角形 B.等腰三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
3、在下列长度的各组线段中,能组成直角三角形的是( )
A.5,6,7 B.1,4,9
C.5,12,13 D.5,11,12
4、在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列条件中,能判断△ABC为直角三角形的是( )
A. a+b=c B. a:b:c=3:4:5 C. a=b=2c D. ∠A=∠B=∠C
5、在ΔABC中,∠A、∠B、∠C的对边分别是a、b、c,下列说法中正确的个数有 ( )
①如果∠B-∠C=∠A,则ΔABC是直角三角形
②如果c2=b2-a2,则ΔABC是直角三角形,且∠C=900
③如果(c+a)(c-a)=b2,则ΔABC是直角三角形
④如果∠A:∠B:∠C =5:2:3,则ΔABC是直角三角形
A. 1 B. 2 C. 3 D.4
6、满足下列条件的△ABC,不是直角三角形的是
A.b2=c2-a2
B.a∶b∶c=3∶4∶5
C.∠C=∠A-∠B
D.∠A∶∠B∶∠C=12∶13∶15
7、一位工人师傅测量一个等腰三角形工件的腰,底及底边上的高, 并按顺序记录下数据,量完后,不小心与其他记录的数据记混了,请你帮助这位师傅从下列数据中找出等腰三角形工件的数据( )
A.13,10,10 B.13,10,12 C.13,12,12 D.13,10,11
8、如果△ABC的三边分别为m2-1,2 m,m2+1(m>1)那么( )
A.△ABC是直角三角形,且斜边长为m2+1
B.△ABC是直角三角形,且斜边长2 为m
C.△ABC是直角三角形,但斜边长需由m的大小确定
D.△ABC不是直角三角形
二、填空题(每题3分,共24分)
1、有一个三角形的两条边长是6和10,要使这个三角形成为直角三角形,则第三边边长为_____________.
2、若一个三角形的三边长为m+1 ,m+2 ,m+3, 当m______时,此三角形是直角三角形.
3、在Rt△ABC中,斜边AB=2,则AB2+BC2+CA2=_______ .
4、 已知|x-12|+|x+y-25|与z2-10z+25互为相反数,则以x、y、z为三边的三角形是______ 三角形.
5、如图1,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,先将直角
边AC沿AD折叠,使它落在斜边AB上,且与AE重合,则CD= .
6、已知两条线段的长分别为15和8,当第三条线段取整数_____时,这三条线段能围成一个直角三角形.
7、分别以下列五组数为一个三角形的边长:①6,8,10 ②13,5,12 ③1,2,3 ④9,40,41⑤,,,其中能构成直角三角形的有__________ 组.
8、以ABC的三条边向外作正方形,依次得到的面积为25, 144, 169, 则这个三角形是________三角形.
三、解答题(共32分)
1、设三角形的三边分别等于下列各组数:①7,8,10 ②7,24,25 ③12,35,37 ④13,11,10;
(1)请判断哪组数所代表的三角形是直角三角形,为什么?
(2)把你判断是Rt△的哪组数作出它所表示的三角形,并用量角器来进行验证.
2、若△ABC的三边a、b、c满足条件a2+b2+c2+338=10a+24b+26c,试判断△ABC的形状.
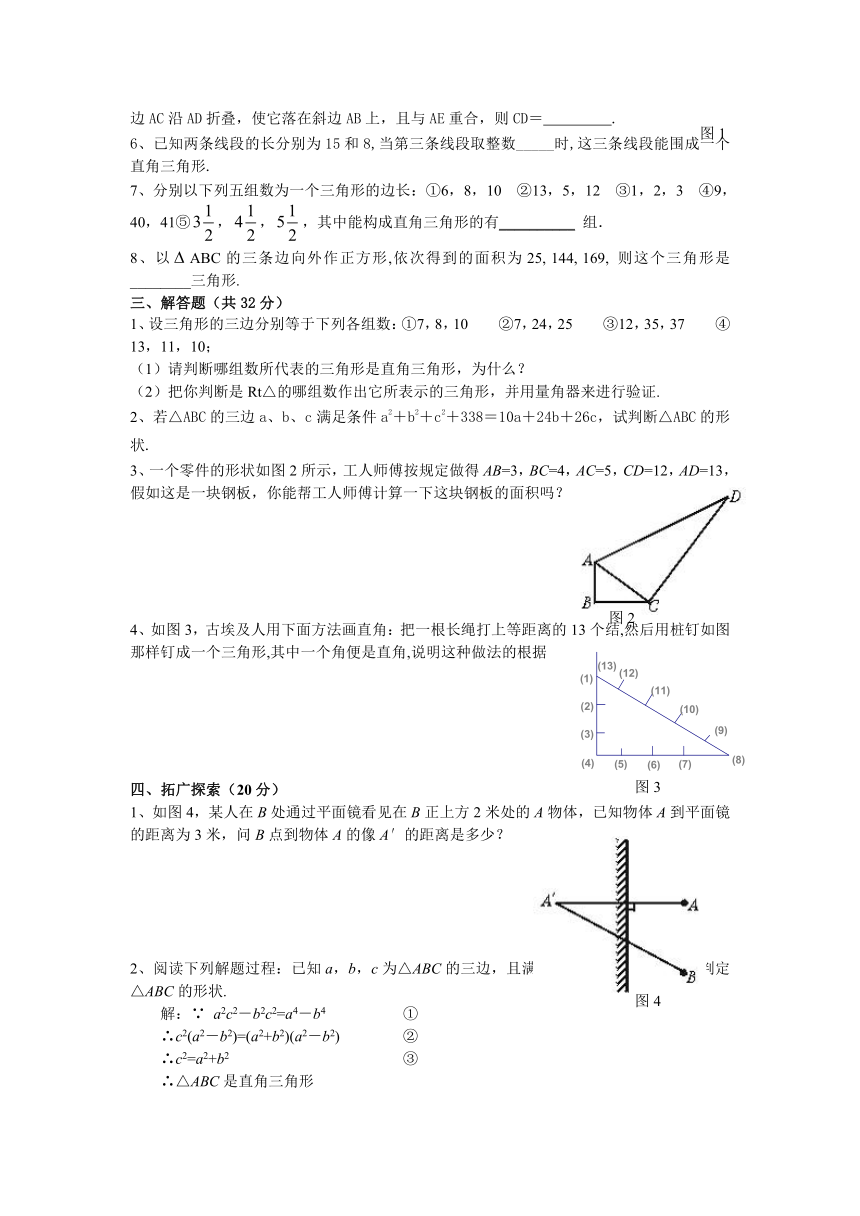
3、一个零件的形状如图2所示,工人师傅按规定做得AB=3,BC=4,AC=5,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?
4、如图3,古埃及人用下面方法画直角:把一根长绳打上等距离的13个结,然后用桩钉如图那样钉成一个三角形,其中一个角便是直角,说明这种做法的根据
四、拓广探索(20分)
1、如图4,某人在B处通过平面镜看见在B正上方2米处的A物体,已知物体A到平面镜的距离为3米,问B点到物体A的像A′的距离是多少?
2、阅读下列解题过程:已知a,b,c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判定△ABC的形状.
解:∵ a2c2-b2c2=a4-b4 ①
∴c2(a2-b2)=(a2+b2)(a2-b2) ②
∴c2=a2+b2 ③
∴△ABC是直角三角形
问:上述解题过程,从哪一步开始出现错误?请写出该步的序号:_________;错误的原因为_________;本题正确的结论是_________.
提升能力,超越自我
1、如图5所示,有两条互相垂直的街道a和b,a路上有一小商店A,b路上有一批发部B.小商店主人每次进货都沿着A—O—B路线到达B处,然后原路返回.已知A,B两处距十字路口O的距离分别为600米、800米,问若小商店主人重新选一条最近的路线,那么往返一趟最多可能比原来少走多少米?
2、阅读下面材料,并解决问题:
(1)如图6,等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5则∠APB=__________,由于PA,PB不在一个三角形中,为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌__________这样,就可以利用全等三角形知识,将三条线段的长度转化到一个三角形中从而求出∠APB的度数.
(2)请你利用第(1)题的解答思想方法,解答下面问题:已知如图7,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2 .
参考答案:
一、1、B;2、D;3、C;4、B;5、B;6、D;7、B;8、A;
二、1、8或;2、2;3、8;4、直角;5、3;6、17;7、3;8、直角三角形;
三、1、(1)②③ ∵72+242=252, 122+352=372 (2)略
2、直角三角形;
3、∵42+32=52,52+122=132,即AB2+BC2=AC2,故∠B=90°,同理,∠ACD=90°,∴S四边形ABCD=S△ABC+S△ACD=×3×4+×5×12=6+30=36.
4、由图形可知:三角形三边的长分别为:3,4,5满足32+42=52,所以三角形是直角三角形;
四、1、由题意知:△ABA′是直角三角形,由轴对称及平面镜成像知:AA′=2×3=6,
∵A′B2=A′A2+AB2=62+22=40,∴A′B=2(米)
2、③;a2-b2可以为零;△ABC为直角三角形或等腰三角形;
提升能力,超越自我
1、由题意,A,O,B三点构成,且,所以.在中,是直角边,故.所以.因为,所以,若小商店主人重新选一条最近的路线,那么往返一趟最多可能比原来少走(米).
2、(1)150° △ABP
(2)证明:将△ABE绕A点旋转到△AC处,此时△ABE≌△AC,BE=C,AE=A=∠CA,∴,连结,
在中,,又
∴≌,∴∴
图1
图2
图3
图4
A
B
O
图5
图7
图6
1、小红要求△ABC最长边上的高,测得AB=8 cm,AC=6 cm,BC=10 cm,则可知最长边上的高是( )
A.48 cm B.4.8 cm
C.0.48 cm D.5 cm
2、已知a,b,c为△ABC三边,且满足a2c2-b2c2=a4-b4,则它的形状为( )
A.直角三角形 B.等腰三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
3、在下列长度的各组线段中,能组成直角三角形的是( )
A.5,6,7 B.1,4,9
C.5,12,13 D.5,11,12
4、在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列条件中,能判断△ABC为直角三角形的是( )
A. a+b=c B. a:b:c=3:4:5 C. a=b=2c D. ∠A=∠B=∠C
5、在ΔABC中,∠A、∠B、∠C的对边分别是a、b、c,下列说法中正确的个数有 ( )
①如果∠B-∠C=∠A,则ΔABC是直角三角形
②如果c2=b2-a2,则ΔABC是直角三角形,且∠C=900
③如果(c+a)(c-a)=b2,则ΔABC是直角三角形
④如果∠A:∠B:∠C =5:2:3,则ΔABC是直角三角形
A. 1 B. 2 C. 3 D.4
6、满足下列条件的△ABC,不是直角三角形的是
A.b2=c2-a2
B.a∶b∶c=3∶4∶5
C.∠C=∠A-∠B
D.∠A∶∠B∶∠C=12∶13∶15
7、一位工人师傅测量一个等腰三角形工件的腰,底及底边上的高, 并按顺序记录下数据,量完后,不小心与其他记录的数据记混了,请你帮助这位师傅从下列数据中找出等腰三角形工件的数据( )
A.13,10,10 B.13,10,12 C.13,12,12 D.13,10,11
8、如果△ABC的三边分别为m2-1,2 m,m2+1(m>1)那么( )
A.△ABC是直角三角形,且斜边长为m2+1
B.△ABC是直角三角形,且斜边长2 为m
C.△ABC是直角三角形,但斜边长需由m的大小确定
D.△ABC不是直角三角形
二、填空题(每题3分,共24分)
1、有一个三角形的两条边长是6和10,要使这个三角形成为直角三角形,则第三边边长为_____________.
2、若一个三角形的三边长为m+1 ,m+2 ,m+3, 当m______时,此三角形是直角三角形.
3、在Rt△ABC中,斜边AB=2,则AB2+BC2+CA2=_______ .
4、 已知|x-12|+|x+y-25|与z2-10z+25互为相反数,则以x、y、z为三边的三角形是______ 三角形.
5、如图1,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,先将直角
边AC沿AD折叠,使它落在斜边AB上,且与AE重合,则CD= .
6、已知两条线段的长分别为15和8,当第三条线段取整数_____时,这三条线段能围成一个直角三角形.
7、分别以下列五组数为一个三角形的边长:①6,8,10 ②13,5,12 ③1,2,3 ④9,40,41⑤,,,其中能构成直角三角形的有__________ 组.
8、以ABC的三条边向外作正方形,依次得到的面积为25, 144, 169, 则这个三角形是________三角形.
三、解答题(共32分)
1、设三角形的三边分别等于下列各组数:①7,8,10 ②7,24,25 ③12,35,37 ④13,11,10;
(1)请判断哪组数所代表的三角形是直角三角形,为什么?
(2)把你判断是Rt△的哪组数作出它所表示的三角形,并用量角器来进行验证.
2、若△ABC的三边a、b、c满足条件a2+b2+c2+338=10a+24b+26c,试判断△ABC的形状.
3、一个零件的形状如图2所示,工人师傅按规定做得AB=3,BC=4,AC=5,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?
4、如图3,古埃及人用下面方法画直角:把一根长绳打上等距离的13个结,然后用桩钉如图那样钉成一个三角形,其中一个角便是直角,说明这种做法的根据
四、拓广探索(20分)
1、如图4,某人在B处通过平面镜看见在B正上方2米处的A物体,已知物体A到平面镜的距离为3米,问B点到物体A的像A′的距离是多少?
2、阅读下列解题过程:已知a,b,c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判定△ABC的形状.
解:∵ a2c2-b2c2=a4-b4 ①
∴c2(a2-b2)=(a2+b2)(a2-b2) ②
∴c2=a2+b2 ③
∴△ABC是直角三角形
问:上述解题过程,从哪一步开始出现错误?请写出该步的序号:_________;错误的原因为_________;本题正确的结论是_________.
提升能力,超越自我
1、如图5所示,有两条互相垂直的街道a和b,a路上有一小商店A,b路上有一批发部B.小商店主人每次进货都沿着A—O—B路线到达B处,然后原路返回.已知A,B两处距十字路口O的距离分别为600米、800米,问若小商店主人重新选一条最近的路线,那么往返一趟最多可能比原来少走多少米?
2、阅读下面材料,并解决问题:
(1)如图6,等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5则∠APB=__________,由于PA,PB不在一个三角形中,为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌__________这样,就可以利用全等三角形知识,将三条线段的长度转化到一个三角形中从而求出∠APB的度数.
(2)请你利用第(1)题的解答思想方法,解答下面问题:已知如图7,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2 .
参考答案:
一、1、B;2、D;3、C;4、B;5、B;6、D;7、B;8、A;
二、1、8或;2、2;3、8;4、直角;5、3;6、17;7、3;8、直角三角形;
三、1、(1)②③ ∵72+242=252, 122+352=372 (2)略
2、直角三角形;
3、∵42+32=52,52+122=132,即AB2+BC2=AC2,故∠B=90°,同理,∠ACD=90°,∴S四边形ABCD=S△ABC+S△ACD=×3×4+×5×12=6+30=36.
4、由图形可知:三角形三边的长分别为:3,4,5满足32+42=52,所以三角形是直角三角形;
四、1、由题意知:△ABA′是直角三角形,由轴对称及平面镜成像知:AA′=2×3=6,
∵A′B2=A′A2+AB2=62+22=40,∴A′B=2(米)
2、③;a2-b2可以为零;△ABC为直角三角形或等腰三角形;
提升能力,超越自我
1、由题意,A,O,B三点构成,且,所以.在中,是直角边,故.所以.因为,所以,若小商店主人重新选一条最近的路线,那么往返一趟最多可能比原来少走(米).
2、(1)150° △ABP
(2)证明:将△ABE绕A点旋转到△AC处,此时△ABE≌△AC,BE=C,AE=A=∠CA,∴,连结,
在中,,又
∴≌,∴∴
图1
图2
图3
图4
A
B
O
图5
图7
图6
