18.2勾股定理的逆定理 测试(2)有答案
文档属性
| 名称 | 18.2勾股定理的逆定理 测试(2)有答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 54.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-07 00:00:00 | ||
图片预览


文档简介
18.2勾股定理的逆定理 测试(2)
一、基础过关:
1、在Rt△ABC中,∠B=90°,BC=15,AC=17,以AB为直径作半圆,则此半圆的面积为( ).
A.16π B.12π C.10π D.8π
2、已知直角三角形两边的长为3和4,则此三角形的周长为( ).
A.12 B.7+
C.12或7+ D.以上都不对
3、梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3m.同时梯子的顶端B下降
至B′,那么BB′( ).
A.小于1m B.大于1m
C.等于1m D.小于或等于1m
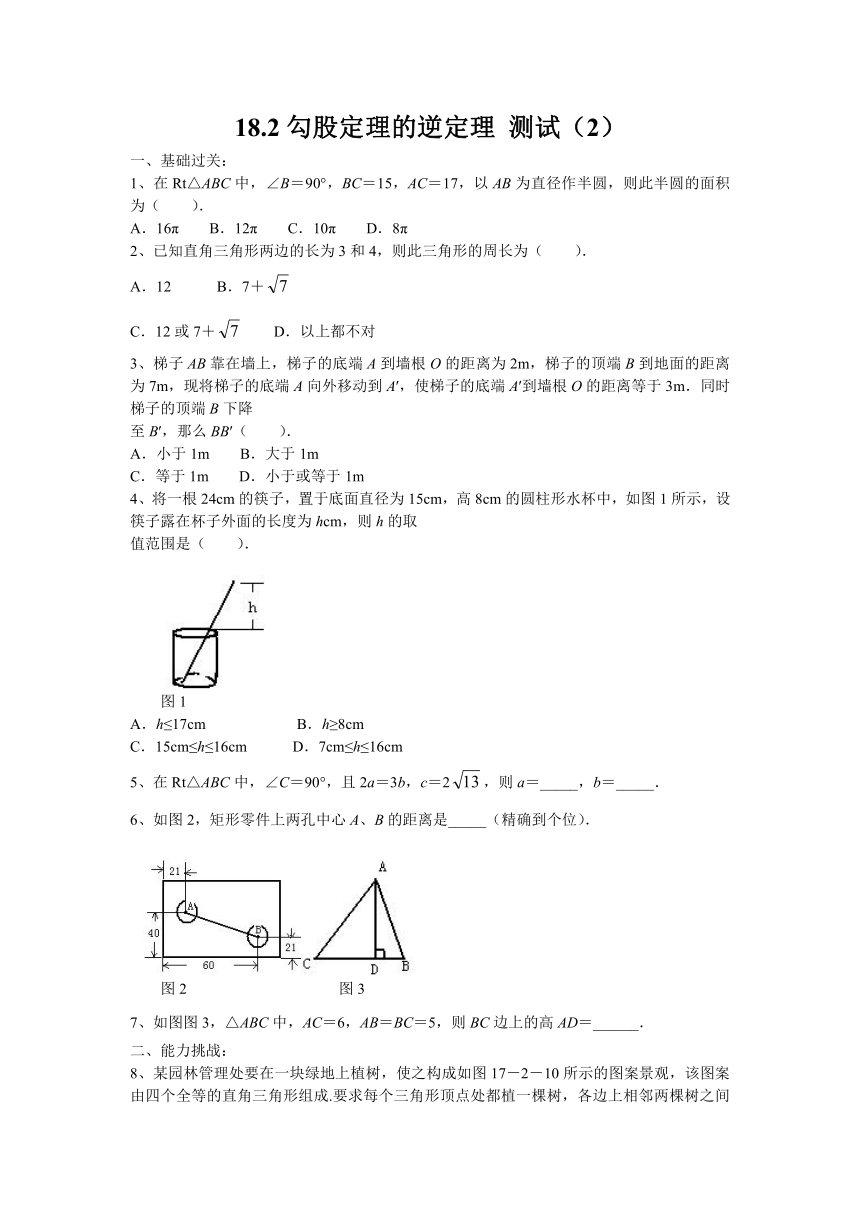
4、将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图1所示,设筷子露在杯子外面的长度为hcm,则h的取
值范围是( ).
图1
A.h≤17cm B.h≥8cm
C.15cm≤h≤16cm D.7cm≤h≤16cm
5、在Rt△ABC中,∠C=90°,且2a=3b,c=2,则a=_____,b=_____.
6、如图2,矩形零件上两孔中心A、B的距离是_____(精确到个位).
图2 图3
7、如图图3,△ABC中,AC=6,AB=BC=5,则BC边上的高AD=______.
二、能力挑战:
8、某园林管理处要在一块绿地上植树,使之构成如图17-2-10所示的图案景观,该图案由四个全等的直角三角形组成.要求每个三角形顶点处都植一棵树,各边上相邻两棵树之间的距离均为1米,如果每个三角形最短边上都植6棵树,那么这四个直角三角形的边上共需植树多少棵.
图4
9、如图5,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去.
(1)记正方形ABCD的边长为a1=1,按上述方法所作的正方形的边长依次为a2,a3,a4,……,an,请求出a2,a3,a4的值;
(2)根据以上规律写出an的表达式.
图5
10、已知:如图6,在△ABC中,∠CAB=120°,AB=4,AC=2,AD⊥BC,D是垂足.求:AD的长.
图6
11、如图7,甲船以16海里/时的速度离开港
口,向东南航行,乙船在同时同地向西南方向航行,已知他们离开港口一个半小时后分别到达B、A两点,且知AB=30海里,问乙船每小时航行多少海里?
图7
三、中考在线:
12、图8甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的。在Rt△ABC中,若直角边AC=6,BC=6,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长(图乙中的实线)是______________。
图8
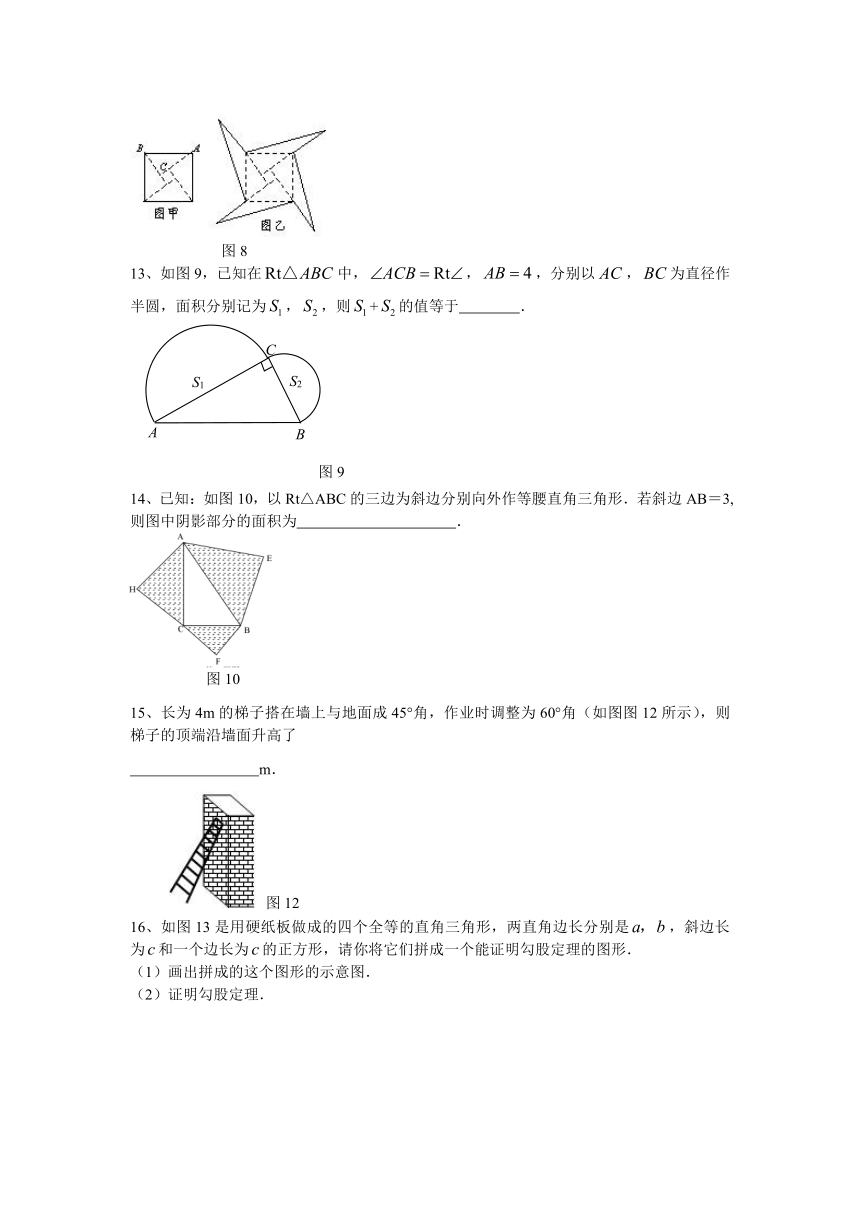
13、如图9,已知在中,,,分别以,为直径作半圆,面积分别记为,,则+的值等于 .
图9
14、已知:如图10,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为 .
图10
15、长为4m的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图图12所示),则梯子的顶端沿墙面升高了
m.
图12
16、如图13是用硬纸板做成的四个全等的直角三角形,两直角边长分别是,斜边长为和一个边长为的正方形,请你将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图.
(2)证明勾股定理.
图13
参考答案
1、D 点拨:在Rt△ABC中,AB2=AC2-BC2=172-152=82,∴AB=8.∴S半圆=πR2=π×()2=8π.故选D;
2、C 点拨:因直角三角形的斜边不明确,结合勾股定理可求得第三边的长为5或,所以直角三角形的周长为3+4+5=12或3+4+=7+,故选C;
3、A 点拨:移动前后梯子的长度不变,即Rt△AOB和Rt△A′OB′的斜边相等.由勾股定理,得32+B′O2=22+72,B′O=,6<B′O<7,则O<BB′<1.故应选A;
4、D 点拨:筷子在杯中的最大长度为=17cm,最短长度为8cm,则筷子露在杯子外面的长度为24-17≤h≤24-8,即7cm≤h≤16cm,故选D.
5.a=b,b=4 点拨:设a=3k,b=2k,由勾股定理,有
(3k)2+(2k)2=(2)2,解得a=b,b=4.;
6.43 点拨:做矩形两边的垂线,构造Rt△ABC,利用勾股定理,AB2=AC2+BC2=192+392=1882,AB≈43;
7.3.6 点拨:设DC=x,则BD=5-x.在Rt△ABD中,AD2=52-(5-x)2,在Rt△ADC中,AD2=62-x2,∴52-(5-x)2=62-x2,x=3.6.故AD==4.8);
8、120 点拨 根据每个三角形顶点处都植一棵树,各边上相邻两棵树之间的距离均为1米,且每个三角形最短边上都植6棵树,可知最短直角边长为5米,从表格中不难发现另外两条边长为12米、13米,因而一个直角三角形的边上植树为:6+13+14-3=30(棵),故四个直角三角形的边上共需植树30×4=120棵.
9、解析:利用勾股定理求斜边长.
(1)∵四边形ABCD是正方形,∴AB=BC=1,∠B=90°.∴在Rt△ABC中,AC===.同理:AE=2,EH=2,…,即a2=,a3=2,a4=2.
(2)an=(n为正整数).
10、解析:解析:过C作CE⊥BE交BA的延长线于E
∵∠CAB=120°,∴∠CAE=60°,∴∠ACE=30°
∵AC=2,∴AE=1
在Rt△ACE中,由勾股定理可得:CE2=AC2-AE2=3
∴CE=
在Rt△BCE中,由勾股定理可得:BC2=CE2+BE2=28
∴BC=
∵AB×CE=CB×AD
∴4×=×AD,∴AD=
11、解析:本题要注意判断角的大小,根据题意知:∠1=∠2=45°,从而证明△ABC为直角三角形,这是解题的前提,然后可运用勾股定理求解.B在O的东南方向,A在O的西南方向,所以∠1=∠2=45°,所以∠AOB=90°,即△AOB为Rt△.BO=16×=24(海里),AB=30海里,根据勾股定理,得AO2=AB2-BO2=302-242=182,所以AO=18.所以乙船的速度=18÷=18×=12(海里/时).
答:乙船每小时航行12海里.
12、答案76
13、答案2π
14、答案
15、【答案】
16、方法一解:(1)如图
(2)证明:大正方形的面积表示为,大正方形的面积也可表示为,,,.即直角三角形两直角边的平方和等于斜边的平方.
方法二解:(1)如图答17-2-3
(2)证明:大正方形的面积表示为:,又可以表示为:,,,.即直角三角形两直角边的平方和等于斜边的平方.
A
B
C
D
E
C
A
B
S1
S2
c
b
a
c
b
a
c
b
a
c
b
a
c
c
a
b
c
c
c
c
b
b
b
a
a
a
a
b
c
一、基础过关:
1、在Rt△ABC中,∠B=90°,BC=15,AC=17,以AB为直径作半圆,则此半圆的面积为( ).
A.16π B.12π C.10π D.8π
2、已知直角三角形两边的长为3和4,则此三角形的周长为( ).
A.12 B.7+
C.12或7+ D.以上都不对
3、梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3m.同时梯子的顶端B下降
至B′,那么BB′( ).
A.小于1m B.大于1m
C.等于1m D.小于或等于1m
4、将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图1所示,设筷子露在杯子外面的长度为hcm,则h的取
值范围是( ).
图1
A.h≤17cm B.h≥8cm
C.15cm≤h≤16cm D.7cm≤h≤16cm
5、在Rt△ABC中,∠C=90°,且2a=3b,c=2,则a=_____,b=_____.
6、如图2,矩形零件上两孔中心A、B的距离是_____(精确到个位).
图2 图3
7、如图图3,△ABC中,AC=6,AB=BC=5,则BC边上的高AD=______.
二、能力挑战:
8、某园林管理处要在一块绿地上植树,使之构成如图17-2-10所示的图案景观,该图案由四个全等的直角三角形组成.要求每个三角形顶点处都植一棵树,各边上相邻两棵树之间的距离均为1米,如果每个三角形最短边上都植6棵树,那么这四个直角三角形的边上共需植树多少棵.
图4
9、如图5,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去.
(1)记正方形ABCD的边长为a1=1,按上述方法所作的正方形的边长依次为a2,a3,a4,……,an,请求出a2,a3,a4的值;
(2)根据以上规律写出an的表达式.
图5
10、已知:如图6,在△ABC中,∠CAB=120°,AB=4,AC=2,AD⊥BC,D是垂足.求:AD的长.
图6
11、如图7,甲船以16海里/时的速度离开港
口,向东南航行,乙船在同时同地向西南方向航行,已知他们离开港口一个半小时后分别到达B、A两点,且知AB=30海里,问乙船每小时航行多少海里?
图7
三、中考在线:
12、图8甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的。在Rt△ABC中,若直角边AC=6,BC=6,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长(图乙中的实线)是______________。
图8
13、如图9,已知在中,,,分别以,为直径作半圆,面积分别记为,,则+的值等于 .
图9
14、已知:如图10,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为 .
图10
15、长为4m的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图图12所示),则梯子的顶端沿墙面升高了
m.
图12
16、如图13是用硬纸板做成的四个全等的直角三角形,两直角边长分别是,斜边长为和一个边长为的正方形,请你将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图.
(2)证明勾股定理.
图13
参考答案
1、D 点拨:在Rt△ABC中,AB2=AC2-BC2=172-152=82,∴AB=8.∴S半圆=πR2=π×()2=8π.故选D;
2、C 点拨:因直角三角形的斜边不明确,结合勾股定理可求得第三边的长为5或,所以直角三角形的周长为3+4+5=12或3+4+=7+,故选C;
3、A 点拨:移动前后梯子的长度不变,即Rt△AOB和Rt△A′OB′的斜边相等.由勾股定理,得32+B′O2=22+72,B′O=,6<B′O<7,则O<BB′<1.故应选A;
4、D 点拨:筷子在杯中的最大长度为=17cm,最短长度为8cm,则筷子露在杯子外面的长度为24-17≤h≤24-8,即7cm≤h≤16cm,故选D.
5.a=b,b=4 点拨:设a=3k,b=2k,由勾股定理,有
(3k)2+(2k)2=(2)2,解得a=b,b=4.;
6.43 点拨:做矩形两边的垂线,构造Rt△ABC,利用勾股定理,AB2=AC2+BC2=192+392=1882,AB≈43;
7.3.6 点拨:设DC=x,则BD=5-x.在Rt△ABD中,AD2=52-(5-x)2,在Rt△ADC中,AD2=62-x2,∴52-(5-x)2=62-x2,x=3.6.故AD==4.8);
8、120 点拨 根据每个三角形顶点处都植一棵树,各边上相邻两棵树之间的距离均为1米,且每个三角形最短边上都植6棵树,可知最短直角边长为5米,从表格中不难发现另外两条边长为12米、13米,因而一个直角三角形的边上植树为:6+13+14-3=30(棵),故四个直角三角形的边上共需植树30×4=120棵.
9、解析:利用勾股定理求斜边长.
(1)∵四边形ABCD是正方形,∴AB=BC=1,∠B=90°.∴在Rt△ABC中,AC===.同理:AE=2,EH=2,…,即a2=,a3=2,a4=2.
(2)an=(n为正整数).
10、解析:解析:过C作CE⊥BE交BA的延长线于E
∵∠CAB=120°,∴∠CAE=60°,∴∠ACE=30°
∵AC=2,∴AE=1
在Rt△ACE中,由勾股定理可得:CE2=AC2-AE2=3
∴CE=
在Rt△BCE中,由勾股定理可得:BC2=CE2+BE2=28
∴BC=
∵AB×CE=CB×AD
∴4×=×AD,∴AD=
11、解析:本题要注意判断角的大小,根据题意知:∠1=∠2=45°,从而证明△ABC为直角三角形,这是解题的前提,然后可运用勾股定理求解.B在O的东南方向,A在O的西南方向,所以∠1=∠2=45°,所以∠AOB=90°,即△AOB为Rt△.BO=16×=24(海里),AB=30海里,根据勾股定理,得AO2=AB2-BO2=302-242=182,所以AO=18.所以乙船的速度=18÷=18×=12(海里/时).
答:乙船每小时航行12海里.
12、答案76
13、答案2π
14、答案
15、【答案】
16、方法一解:(1)如图
(2)证明:大正方形的面积表示为,大正方形的面积也可表示为,,,.即直角三角形两直角边的平方和等于斜边的平方.
方法二解:(1)如图答17-2-3
(2)证明:大正方形的面积表示为:,又可以表示为:,,,.即直角三角形两直角边的平方和等于斜边的平方.
A
B
C
D
E
C
A
B
S1
S2
c
b
a
c
b
a
c
b
a
c
b
a
c
c
a
b
c
c
c
c
b
b
b
a
a
a
a
b
c
