数学下学期人教A版选修2-3第二章2.1.1离散型随机变量及其分布列课件(共20张PPT)
文档属性
| 名称 | 数学下学期人教A版选修2-3第二章2.1.1离散型随机变量及其分布列课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-30 21:19:31 | ||
图片预览








文档简介
(共20张PPT)
2.1离散型随机变量及其分布列
复习引入:
1、什么是随机事件?什么是基本事件?
在一定条件下可能发生也可能不发生的事件,叫做随机事件。试验的每一个可能的结果称为基本事件。
2、什么是随机试验?
凡是对现象或为此而进行的实验,都称之为试验。
如果试验具有下述特点:
试验可以在相同条件下重复进行;每次试验的所有可能结果都是明确可知的,并且不止一个;每次试验总是恰好出现这些结果中的一个,但在一次试验之前却不能肯定这次试验会出现哪一个结果。它被称为一个随机试验。简称试验。
问题
1.
你能说出下列各试验的结果吗?
各试验结果是否能用数量表示?
(1)
掷一枚骰子;
(2)
掷一枚硬币;
(3)
测一病人体温.
掷一枚骰子的试验结果有:
1
点向上,
2
点向上,
3
点向上,
4
点向上,
5
点向上,
6
点向上.
可分别用
数字
1,
2,
3,
4,
5,
6
表示上面的六个试验结果.
析:(1)
(2)
掷一枚硬币的试验结果有:
正面向上,
反面向上.
我们可用数字
1
表示
“正面向上”,
用
0
表示
“反面向
上”.
(3)
测一病人体温的试验,
可能出现的结果有很多,
这些结果不能一一举出.
如果我们只关心其体温是否正常,
还是低热,
还是
高烧,
那么试验结果有:
正常,
低热,
高烧三个结果.
我们可用数字
0
表示
“正常”,
用
1
表示
“低热”,
用
2
表示
“高烧”.
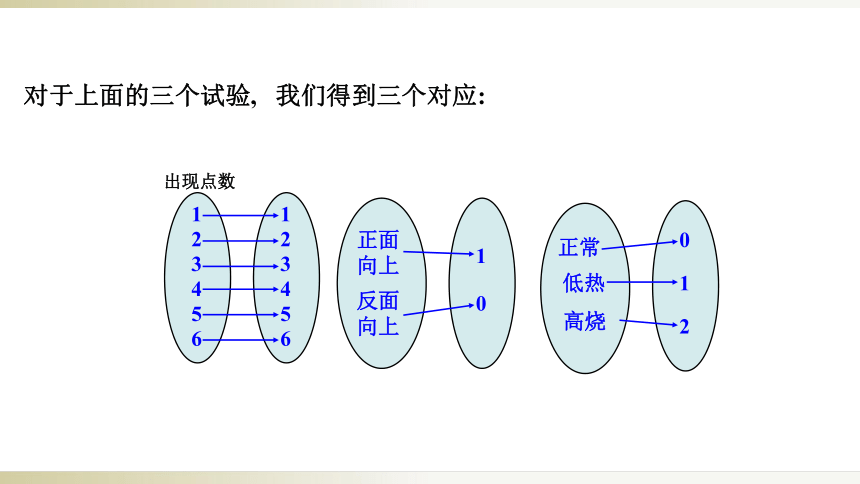
对于上面的三个试验,
我们得到三个对应:
出现点数
1
2
3
4
5
6
1
2
3
4
5
6
1
0
正面向上
反面向上
1
2
正常
低热
高烧
0
1.随机变量的概念
(1)如上的三个试验中都有一个对应关系,
使得每一个试验结果都用一个确定的数字表示.
在这样的对应关系下,
数字随着试验结果的变化而变化:像这种随着试验结果变化而变化的变量称为随机变量.
(2)随机变量也是一种映射,
与函数比较,
函数是把实数映射为实数,
随机变量是把试验结果映射为实数.试验结果的范围相当于函数的定义域,
随机变量的取值范围相当于函数的值域.
例1、一个袋中装有5个白球和5个黑球,若从中任取3个,则其中所含白球的个数x
就是一个随机变量,求x
的取值范围,并说明x
的不同取值所表示的事件。
解:
x
的取值范围是{0,1,2,3}
,其中
{x
=0}表示的事件是“取出0个白球,3个黑球”;
{x
=1}表示的事件是“取出1个白球,2个黑球”;
{x
=2}表示的事件是“取出2个白球,1个黑球”;
{x
=3}表示的事件是“取出3个白球,0个黑球”;
变题:{x
<
3}在这里又表示什么事件呢?
“取出的3个球中,白球不超过2个”
2.离散型随机变量
所有取值可以一一列举出的随机变量,称为离散型随机变量.
如:用病人的体温表示试验结果,
可能出现的结果不能一一列举,
不是离散随机变量.
如果关心的是体温是否正常,还是低热,还是高烧,试验结果可以一一列举,这样的随机变量就是离散随机变量.
变量
X=0
表示
“体温正常”,X=1表示
“低热”,X=2
表示
“高烧”.X
的取值范围是
{0,
1,
2}.
离散型随机变量的例子
如:
某人投10个篮的进球数.
某同学一天内接到手机电话的次数.
某城市一年内下雨的天数.
一公交车在某站下车的人数.
某同学短跑后一分钟的心跳次数.
某商店某种商品一天内的售出件数.
……
探究袋子中有3个红球,2个白球,1个黑球,这些球除颜色外完全相同,现要从中摸一个球出来,若摸到黑球得1分,摸到白球得0分,摸到红球倒扣1分,试写出从该盒内随机取出一球所得分数X的概率.
解:因为只取1球,所以X的取值只能是1,0,-1
∴从袋子中随机取出一球所得分数X的分布列为:
X
1
0
-1
P
3.离散型随机变量的分布列:
一般地,若离散型随机变量X
可能取的不同值为:
x1,x2,…,xi,…,xn
X取每一个xi
(i=1,2,…,n)的概率P(X=xi)=Pi,则称表:
X
x1
x2
…
xi
…
P
P1
P2
…
Pi
…
为离散型随机变量X的概率分布列,简称为X的分布列.有时为了表达简单,也用等式
P(X=xi)=Pi
i=1,2,…,n
来表示X的分布列
离散型随机变量的分布列应注意问题:
X
x1
x2
…
xi
…
P
P1
P2
…
Pi
…
1、分布列的构成:
(1)列出了离散型随机变量X的所有取值;
(2)求出了X的每一个取值的概率;
2、分布列的性质:
例2、在掷一枚图钉的随机试验中,令
如果针尖向上的概率为p,试写出随机变量X的分布列。
解:根据分布列的性质,针尖向下的概率是(1-p),于是,随机变量X的分布列是
X
0
1
P
1-p
p
像上面这样的分布列称为两点分布列。
如果随机变量X的分布列为两点分布列,就称X服从两点分布,而称p=P(X=1)为成功概率。
求离散型随机变量分布列的基本步骤:
(1)确定随机变量的所有可能的值xi
(2)求出各取值的概率P(X=xi)=pi
(3)列出表格
定值
求概率
列表
课堂练习:
0.3
0.16
P
3
2
1
0
-1
ξ
2、若随机变量ξ的分布列如下表所示,则常数a=_____
C
课堂练习:
0.88
思考:一个口袋有5只同样大小的球,编号分别为1,2,
3,4,5,从中同时取出3只,以X表示取出的球最小的
号码,求X的分布列。
解:因为同时取出3个球,故X的取值只能是1,2,3
当X=1时,其他两球可在剩余的4个球中任选
故其概率为
当X=2时,其他两球的编号在3,4,5中选,
故其概率为
当X=3时,只可能是3,4,5这种情况,
概率为
X
1
2
3
P
∴随机变量X的分布列为
思考:一个口袋有5只同样大小的球,编号分别为1,2,3,4,5,从中同时取出3只,以X表示取出的球最小的
号码,求X的分布列。
小结:
一、随机变量的定义:
二、离散型随机变量的定义:
三、随机变量的分布列:
1、分布列的性质:
2、求分布列的步骤:
定值
求概率
列表
作业:
1.整理本节知识,预习P47-P48,理解超几何分布。
2.作业本:课本P49
A组第5、6题
,B组1题。
2.1离散型随机变量及其分布列
复习引入:
1、什么是随机事件?什么是基本事件?
在一定条件下可能发生也可能不发生的事件,叫做随机事件。试验的每一个可能的结果称为基本事件。
2、什么是随机试验?
凡是对现象或为此而进行的实验,都称之为试验。
如果试验具有下述特点:
试验可以在相同条件下重复进行;每次试验的所有可能结果都是明确可知的,并且不止一个;每次试验总是恰好出现这些结果中的一个,但在一次试验之前却不能肯定这次试验会出现哪一个结果。它被称为一个随机试验。简称试验。
问题
1.
你能说出下列各试验的结果吗?
各试验结果是否能用数量表示?
(1)
掷一枚骰子;
(2)
掷一枚硬币;
(3)
测一病人体温.
掷一枚骰子的试验结果有:
1
点向上,
2
点向上,
3
点向上,
4
点向上,
5
点向上,
6
点向上.
可分别用
数字
1,
2,
3,
4,
5,
6
表示上面的六个试验结果.
析:(1)
(2)
掷一枚硬币的试验结果有:
正面向上,
反面向上.
我们可用数字
1
表示
“正面向上”,
用
0
表示
“反面向
上”.
(3)
测一病人体温的试验,
可能出现的结果有很多,
这些结果不能一一举出.
如果我们只关心其体温是否正常,
还是低热,
还是
高烧,
那么试验结果有:
正常,
低热,
高烧三个结果.
我们可用数字
0
表示
“正常”,
用
1
表示
“低热”,
用
2
表示
“高烧”.
对于上面的三个试验,
我们得到三个对应:
出现点数
1
2
3
4
5
6
1
2
3
4
5
6
1
0
正面向上
反面向上
1
2
正常
低热
高烧
0
1.随机变量的概念
(1)如上的三个试验中都有一个对应关系,
使得每一个试验结果都用一个确定的数字表示.
在这样的对应关系下,
数字随着试验结果的变化而变化:像这种随着试验结果变化而变化的变量称为随机变量.
(2)随机变量也是一种映射,
与函数比较,
函数是把实数映射为实数,
随机变量是把试验结果映射为实数.试验结果的范围相当于函数的定义域,
随机变量的取值范围相当于函数的值域.
例1、一个袋中装有5个白球和5个黑球,若从中任取3个,则其中所含白球的个数x
就是一个随机变量,求x
的取值范围,并说明x
的不同取值所表示的事件。
解:
x
的取值范围是{0,1,2,3}
,其中
{x
=0}表示的事件是“取出0个白球,3个黑球”;
{x
=1}表示的事件是“取出1个白球,2个黑球”;
{x
=2}表示的事件是“取出2个白球,1个黑球”;
{x
=3}表示的事件是“取出3个白球,0个黑球”;
变题:{x
<
3}在这里又表示什么事件呢?
“取出的3个球中,白球不超过2个”
2.离散型随机变量
所有取值可以一一列举出的随机变量,称为离散型随机变量.
如:用病人的体温表示试验结果,
可能出现的结果不能一一列举,
不是离散随机变量.
如果关心的是体温是否正常,还是低热,还是高烧,试验结果可以一一列举,这样的随机变量就是离散随机变量.
变量
X=0
表示
“体温正常”,X=1表示
“低热”,X=2
表示
“高烧”.X
的取值范围是
{0,
1,
2}.
离散型随机变量的例子
如:
某人投10个篮的进球数.
某同学一天内接到手机电话的次数.
某城市一年内下雨的天数.
一公交车在某站下车的人数.
某同学短跑后一分钟的心跳次数.
某商店某种商品一天内的售出件数.
……
探究袋子中有3个红球,2个白球,1个黑球,这些球除颜色外完全相同,现要从中摸一个球出来,若摸到黑球得1分,摸到白球得0分,摸到红球倒扣1分,试写出从该盒内随机取出一球所得分数X的概率.
解:因为只取1球,所以X的取值只能是1,0,-1
∴从袋子中随机取出一球所得分数X的分布列为:
X
1
0
-1
P
3.离散型随机变量的分布列:
一般地,若离散型随机变量X
可能取的不同值为:
x1,x2,…,xi,…,xn
X取每一个xi
(i=1,2,…,n)的概率P(X=xi)=Pi,则称表:
X
x1
x2
…
xi
…
P
P1
P2
…
Pi
…
为离散型随机变量X的概率分布列,简称为X的分布列.有时为了表达简单,也用等式
P(X=xi)=Pi
i=1,2,…,n
来表示X的分布列
离散型随机变量的分布列应注意问题:
X
x1
x2
…
xi
…
P
P1
P2
…
Pi
…
1、分布列的构成:
(1)列出了离散型随机变量X的所有取值;
(2)求出了X的每一个取值的概率;
2、分布列的性质:
例2、在掷一枚图钉的随机试验中,令
如果针尖向上的概率为p,试写出随机变量X的分布列。
解:根据分布列的性质,针尖向下的概率是(1-p),于是,随机变量X的分布列是
X
0
1
P
1-p
p
像上面这样的分布列称为两点分布列。
如果随机变量X的分布列为两点分布列,就称X服从两点分布,而称p=P(X=1)为成功概率。
求离散型随机变量分布列的基本步骤:
(1)确定随机变量的所有可能的值xi
(2)求出各取值的概率P(X=xi)=pi
(3)列出表格
定值
求概率
列表
课堂练习:
0.3
0.16
P
3
2
1
0
-1
ξ
2、若随机变量ξ的分布列如下表所示,则常数a=_____
C
课堂练习:
0.88
思考:一个口袋有5只同样大小的球,编号分别为1,2,
3,4,5,从中同时取出3只,以X表示取出的球最小的
号码,求X的分布列。
解:因为同时取出3个球,故X的取值只能是1,2,3
当X=1时,其他两球可在剩余的4个球中任选
故其概率为
当X=2时,其他两球的编号在3,4,5中选,
故其概率为
当X=3时,只可能是3,4,5这种情况,
概率为
X
1
2
3
P
∴随机变量X的分布列为
思考:一个口袋有5只同样大小的球,编号分别为1,2,3,4,5,从中同时取出3只,以X表示取出的球最小的
号码,求X的分布列。
小结:
一、随机变量的定义:
二、离散型随机变量的定义:
三、随机变量的分布列:
1、分布列的性质:
2、求分布列的步骤:
定值
求概率
列表
作业:
1.整理本节知识,预习P47-P48,理解超几何分布。
2.作业本:课本P49
A组第5、6题
,B组1题。
