2.2.2 椭圆的几何性质 课件-2020-2021学年人教版高中数学选修2-1(共22张PPT)
文档属性
| 名称 | 2.2.2 椭圆的几何性质 课件-2020-2021学年人教版高中数学选修2-1(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 934.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-30 21:26:35 | ||
图片预览






文档简介
(共22张PPT)
请同学们思考:解析几何研究的主要问题是什么?
(1)根据已知条件,求出表示曲线的方程
(2)通过曲线的方程,研究曲线的性质
一、复习:
1.椭圆的定义:
2.椭圆的标准方程是:
3.椭圆中a,b,c的关系是:
当焦点在X轴上时
当焦点在Y轴上时
a2=b2+c2
平面内与两定点F1、F2的距离
为常数
的动点的轨迹叫做椭圆。
之和
(大于|F1F2
|)
椭圆的简单几何性质
高中数学(人教A版)选修2-1第二章《椭圆的简单几何性质》
新源二中
鲁辉
二、新课讲解
Y
X
O
能否利用方程(代数方法)研究它的性质
-a≤x≤a,
-b≤y≤b
o
y
B2
B1
A1
A2
F1
F2
c
a
b
1、范围:
观察:椭圆
椭圆落在x=±a,
y=
±
b组成的矩形中
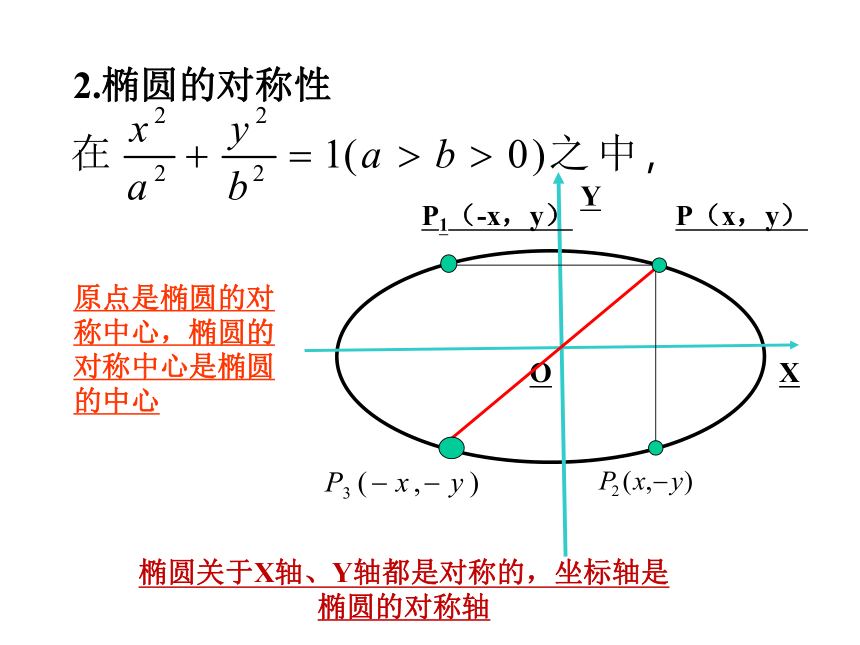
2.椭圆的对称性
Y
X
O
P(x,y)
P1(-x,y)
椭圆关于X轴、Y轴都是对称的,坐标轴是椭圆的对称轴
原点是椭圆的对称中心,椭圆的对称中心是椭圆的中心
Y
X
O
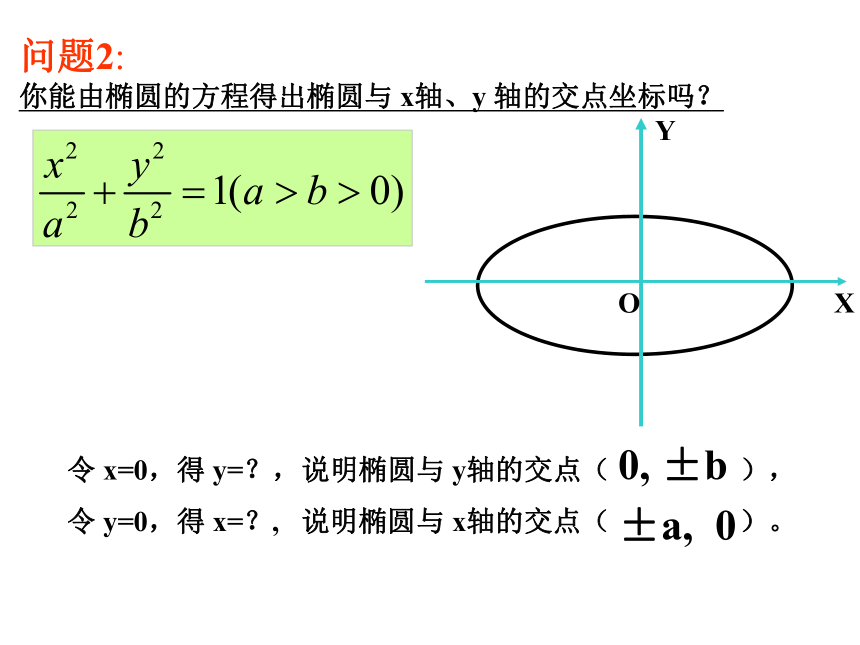
问题2:
你能由椭圆的方程得出椭圆与
x轴、y
轴的交点坐标吗?
令
x=0,得
y=?,说明椭圆与
y轴的交点(
),
令
y=0,得
x=?,
说明椭圆与
x轴的交点(
)。
0,
±b
±a,
0
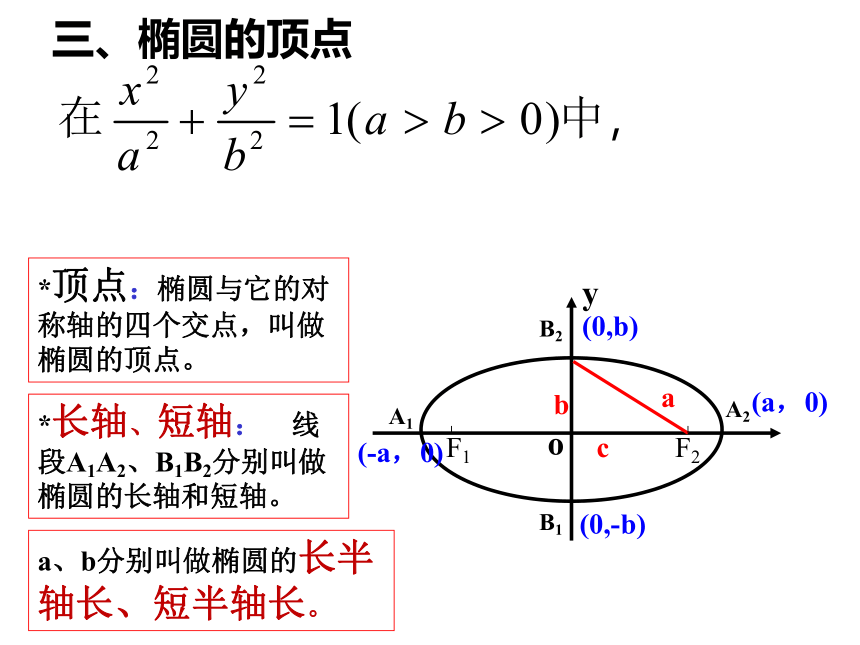
三、椭圆的顶点
顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
长轴、短轴:
线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长、短半轴长。
o
y
B2
B1
A1
A2
F1
F2
c
a
b
(0,b)
(a,0)
(0,-b)
(-a,0)
1
2
3
-1
-2
-3
-4
4
y
1
2
3
-1
-2
-3
-4
4
y
1
2
3
4
5
-1
-5
-2
-3
-4
x
1
2
3
4
5
-1
-5
-2
-3
-4
x
根据前面所学有关知识画出下列图形
(1)
(2)
A1
B1
A2
B2
B2
A2
B1
A1
这两个椭圆的形状有什么不同?
思考:椭圆的圆扁程度究竟与哪些量有关呢?
四、椭圆的离心率
离心率:椭圆的焦距与长轴长的比:
叫做椭圆的离心率。
[1]离心率的取值范围:
[2]离心率对椭圆形状的影响:
01)e
越接近
1,c
就越接近
a,从而
b就越小,椭圆就越扁
2)e
越接近
0,c
就越接近
0,从而
b就越大,椭圆就越圆
[3]e与a,b的关系:
定
义
图
形
方
程
范
围
对称性
焦
点
顶
点
离心率
F1
F2
M
y
x
O
y
x
O
M
F1
F2
|MF1|+|MF2|=2a
(2a>|F1F2|)
(c,0)、(?c,0)
(0,c)、(0,?c)
(?a,0)、(0,?b)
|x|?
a
|y|?
b
|x|?
b
|y|?
a
关于x轴、y轴、原点对称
(?b,0)、(0,?a)
小结:
一个框,四个点,注意光滑和圆扁,莫忘对称要体现
例1已知椭圆方程为16x2+25y2=400,
它的长轴长是:
。短轴长是:
。
焦距是:
。
离心率等于:
。
焦点坐标是:
。顶点坐标是:
。
外切矩形的面积等于:
。
10
8
6
80
解题的关键:1、将椭圆方程转化为标准方程
明确a、b
2、确定焦点的位置和长轴的位置
已知椭圆方程为6x2+y2=6
它的长轴长是:
。短轴长是:
。
焦距是:
.离心率等于:
。
焦点坐标是:
。顶点坐标是:
。
外切矩形的面积等于:
。
2
练习1.
例2.过适合下列条件的椭圆的标准方程:
(1)经过点
、
;
(2)长轴长等于
,离心率等于
.
解:(1)由题意,
,又∵长轴在
轴上,所以,椭圆的标准方程为
.
(2)由已知,
,
∴
,
,∴
,
所以椭圆的标准方程为
或
.
例3.已知椭圆的中心在原点,焦点在坐标轴上,长轴是短轴的三倍,且椭圆经过点P(3,0),求椭圆的方程。
答案:
分类讨论的数学思想
小结:
1.知识小结:
(1)
学习了椭圆的范围、对称性、顶点坐标、离心率等概念及其几何意义。
(2)
研究了椭圆的几个基本量a,b,c,e及顶点、焦点、对称中心及其相互之间的关系
2.数学思想方法:
(1)数与形的结合,用代数的方法解决几何问题。
(2)分类讨论的数学思想
作业:
1.正本作业:教材习题2.2A组第4、5题;
2.课外作业:
《金榜夺冠》椭圆的简单几何性质(一)
:
(必做:)“目标训练”4-6、“达标练习”1、5
(选做:)
P24第2、3题、“备选题”
巩固练习:
1.
若点P(x,y)在椭圆
上,则点P(x,y)横坐标x的取值范围
?
3.
中心在原点,焦点在x轴上,长轴、短轴的长分别为8和6的椭圆方程为
?
4.说出椭圆
的长轴长,短轴长,顶点和焦点坐标
2.若点P(2,4)在椭圆
上,下列是椭圆上的点有
(1)P(-2,4)
(2)P(-4,2)
(3)
P(-2,-4)
(4)P(2,-4)
已知椭圆
的离心率
,求
的值
由
,得:
解:当椭圆的焦点在
轴上时,
,
,得
.
当椭圆的焦点在
轴上时,
,
,得
.
由
,得
,即
.
∴满足条件的
或
.
思考:
再见
谢谢参与
请同学们思考:解析几何研究的主要问题是什么?
(1)根据已知条件,求出表示曲线的方程
(2)通过曲线的方程,研究曲线的性质
一、复习:
1.椭圆的定义:
2.椭圆的标准方程是:
3.椭圆中a,b,c的关系是:
当焦点在X轴上时
当焦点在Y轴上时
a2=b2+c2
平面内与两定点F1、F2的距离
为常数
的动点的轨迹叫做椭圆。
之和
(大于|F1F2
|)
椭圆的简单几何性质
高中数学(人教A版)选修2-1第二章《椭圆的简单几何性质》
新源二中
鲁辉
二、新课讲解
Y
X
O
能否利用方程(代数方法)研究它的性质
-a≤x≤a,
-b≤y≤b
o
y
B2
B1
A1
A2
F1
F2
c
a
b
1、范围:
观察:椭圆
椭圆落在x=±a,
y=
±
b组成的矩形中
2.椭圆的对称性
Y
X
O
P(x,y)
P1(-x,y)
椭圆关于X轴、Y轴都是对称的,坐标轴是椭圆的对称轴
原点是椭圆的对称中心,椭圆的对称中心是椭圆的中心
Y
X
O
问题2:
你能由椭圆的方程得出椭圆与
x轴、y
轴的交点坐标吗?
令
x=0,得
y=?,说明椭圆与
y轴的交点(
),
令
y=0,得
x=?,
说明椭圆与
x轴的交点(
)。
0,
±b
±a,
0
三、椭圆的顶点
顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
长轴、短轴:
线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长、短半轴长。
o
y
B2
B1
A1
A2
F1
F2
c
a
b
(0,b)
(a,0)
(0,-b)
(-a,0)
1
2
3
-1
-2
-3
-4
4
y
1
2
3
-1
-2
-3
-4
4
y
1
2
3
4
5
-1
-5
-2
-3
-4
x
1
2
3
4
5
-1
-5
-2
-3
-4
x
根据前面所学有关知识画出下列图形
(1)
(2)
A1
B1
A2
B2
B2
A2
B1
A1
这两个椭圆的形状有什么不同?
思考:椭圆的圆扁程度究竟与哪些量有关呢?
四、椭圆的离心率
离心率:椭圆的焦距与长轴长的比:
叫做椭圆的离心率。
[1]离心率的取值范围:
[2]离心率对椭圆形状的影响:
0
越接近
1,c
就越接近
a,从而
b就越小,椭圆就越扁
2)e
越接近
0,c
就越接近
0,从而
b就越大,椭圆就越圆
[3]e与a,b的关系:
定
义
图
形
方
程
范
围
对称性
焦
点
顶
点
离心率
F1
F2
M
y
x
O
y
x
O
M
F1
F2
|MF1|+|MF2|=2a
(2a>|F1F2|)
(c,0)、(?c,0)
(0,c)、(0,?c)
(?a,0)、(0,?b)
|x|?
a
|y|?
b
|x|?
b
|y|?
a
关于x轴、y轴、原点对称
(?b,0)、(0,?a)
小结:
一个框,四个点,注意光滑和圆扁,莫忘对称要体现
例1已知椭圆方程为16x2+25y2=400,
它的长轴长是:
。短轴长是:
。
焦距是:
。
离心率等于:
。
焦点坐标是:
。顶点坐标是:
。
外切矩形的面积等于:
。
10
8
6
80
解题的关键:1、将椭圆方程转化为标准方程
明确a、b
2、确定焦点的位置和长轴的位置
已知椭圆方程为6x2+y2=6
它的长轴长是:
。短轴长是:
。
焦距是:
.离心率等于:
。
焦点坐标是:
。顶点坐标是:
。
外切矩形的面积等于:
。
2
练习1.
例2.过适合下列条件的椭圆的标准方程:
(1)经过点
、
;
(2)长轴长等于
,离心率等于
.
解:(1)由题意,
,又∵长轴在
轴上,所以,椭圆的标准方程为
.
(2)由已知,
,
∴
,
,∴
,
所以椭圆的标准方程为
或
.
例3.已知椭圆的中心在原点,焦点在坐标轴上,长轴是短轴的三倍,且椭圆经过点P(3,0),求椭圆的方程。
答案:
分类讨论的数学思想
小结:
1.知识小结:
(1)
学习了椭圆的范围、对称性、顶点坐标、离心率等概念及其几何意义。
(2)
研究了椭圆的几个基本量a,b,c,e及顶点、焦点、对称中心及其相互之间的关系
2.数学思想方法:
(1)数与形的结合,用代数的方法解决几何问题。
(2)分类讨论的数学思想
作业:
1.正本作业:教材习题2.2A组第4、5题;
2.课外作业:
《金榜夺冠》椭圆的简单几何性质(一)
:
(必做:)“目标训练”4-6、“达标练习”1、5
(选做:)
P24第2、3题、“备选题”
巩固练习:
1.
若点P(x,y)在椭圆
上,则点P(x,y)横坐标x的取值范围
?
3.
中心在原点,焦点在x轴上,长轴、短轴的长分别为8和6的椭圆方程为
?
4.说出椭圆
的长轴长,短轴长,顶点和焦点坐标
2.若点P(2,4)在椭圆
上,下列是椭圆上的点有
(1)P(-2,4)
(2)P(-4,2)
(3)
P(-2,-4)
(4)P(2,-4)
已知椭圆
的离心率
,求
的值
由
,得:
解:当椭圆的焦点在
轴上时,
,
,得
.
当椭圆的焦点在
轴上时,
,
,得
.
由
,得
,即
.
∴满足条件的
或
.
思考:
再见
谢谢参与
