山东省恒台第二中学2012届高三12月模块检测数学(理)试题
文档属性
| 名称 | 山东省恒台第二中学2012届高三12月模块检测数学(理)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 270.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-07 00:00:00 | ||
图片预览



文档简介
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共6页。满分150分,考试时间120分钟。考试结束后,将本试卷以及答题卡和答题纸一并交回。答卷前,考生务必将自己的姓名、准考证号、考试科目填涂在试卷、答题卡和答题纸规定的地方。
第Ⅰ卷
注意事项:第Ⅰ卷为选择题,共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一个最符合题目要求。每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选择其他答案标号。不能直接写在本试卷上。
选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1已知△ABC中,,则( )
(A) (B) (C) (D)
2.设复数是实数,则实数
( )
A. B. C. D.
3.已知向量,且,则向量与的夹角为 ( )
A.60° B.120° C.135° D.150°
4.若等差数列{an}的前5项和S5=30,且a2=7,则a7 = ( )
A.0 B.1 C.2 D.3
5. 将函数的图象向左平移个单位,再向上平移1个单位,所得图象的函
数解析式是( )
A. B. C. D.
6.函数f(x)=的图象是( )
7.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是( )
A. B. C. D.
8.设f(x)=则f(ln3)= ( )
A. ln3-1 B. C.e D.3e
9. 曲线在点(2, 4)处的切线方程是( )
A. B. C. D.
10.如图,ABCD-A1B1C1D1为正方体,下面结论错误的是 ( )
A.BD∥平面CB1D1 B.AC1⊥BD
C.异面直线与所成的角为 D.AC1⊥平面CB1D1
11.定义在R上的偶函数f(x)在上递增,,则满足>0的x的取值范围是 ( )
A. B. C. D.
12.设函数在内有定义,对于给定的正数K,定义函数
取函数,=时,函数的调递增区间为( )
A . B. C . D .
第Ⅱ卷
注意事项:
第Ⅱ卷共90分。第II卷所有题目的答案考生必须将用黑色签字笔、钢笔或圆珠笔答在规定位置。
二、填空题:(本大题共4小题,每小题4分,共16分.)
13.若,则= .
14.设变量x,y满足约束条件则目标函数的最大值为 .
15.已知直线是曲线的切线,则 .
16.定义在R上的偶函数在[—1,0]上是增函数,给出下列关于的判断;是周期函数;关于直线对称;是[0,1]上是增函数;在[1,2]上是减函数;关于(,0)中心对称;。
其中所有正确的序号是 。
三、解答题:本大题共6小题,共74分.解答应写文字说明,证明过程或演算步骤.
17.(本小题满分12分)
设函数的最小正周期为.
(Ⅰ)求的值.
(Ⅱ)若函数的图像是由的图像向右平移个单位长度得到,求的单调增区间.
18. (本小题满分12分)
在等比数列中,,且,是和的等差中项.
(I)求数列的通项公式;
(II)若数列满足,求数列的前项和.
19. (本小题满分12分)
口袋中装有质地大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸一个球,记下编号,放回后乙再摸一个球,记下编号。如果两个编号的和为偶数就算甲胜,否则算乙胜。
(1)求甲胜且编号和为6的事件发生的概率;
(2)这种游戏规则公平吗?说明理由。
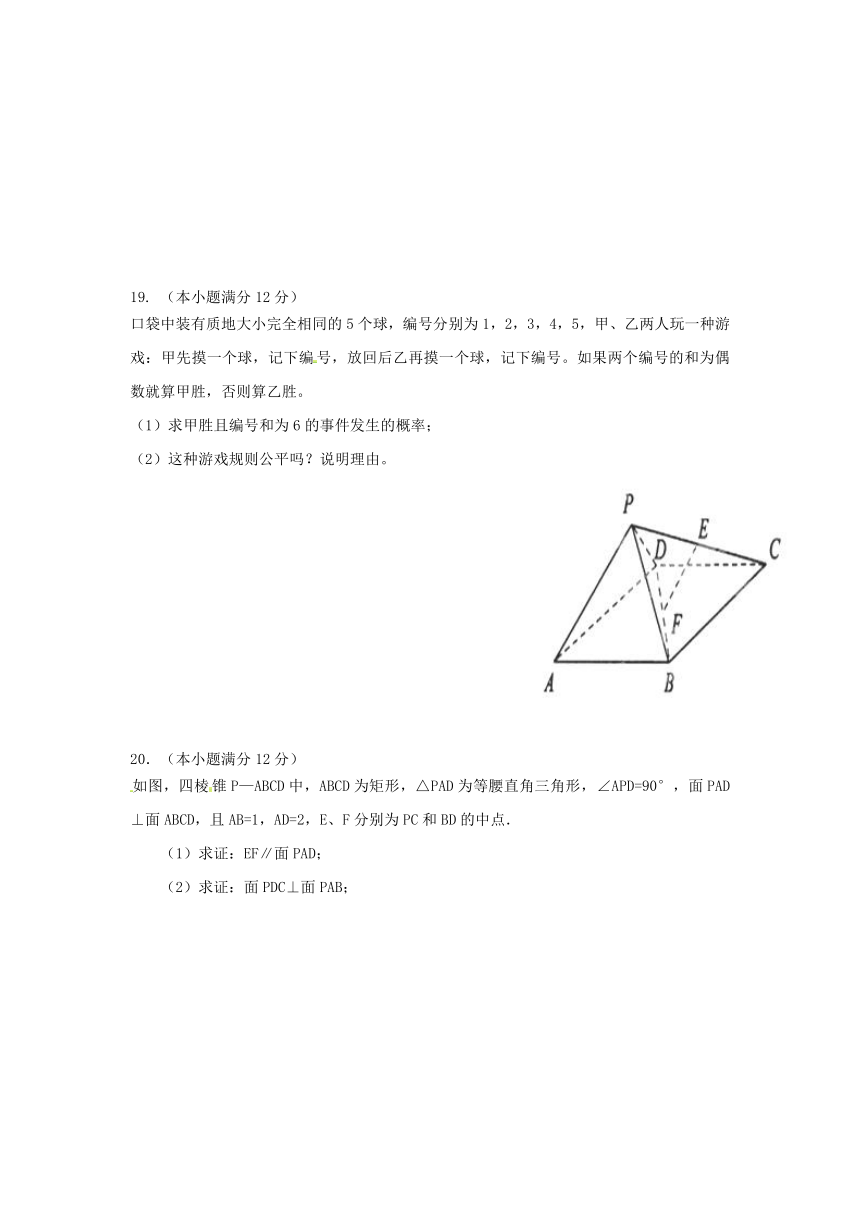
20.(本小题满分12分)
如图,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.
(1)求证:EF∥面PAD;
(2)求证:面PDC⊥面PAB;
21.(本小题满分12分)
某厂家拟对一商品举行促销活动,当该商品的售价为元时,全年的促销费用为万元;根据以往的销售经验,实施促销后的年销售量万件,其中4为常数.当该商品的售价为6元时,年销售量为49万件.
(Ⅰ)求出的值;
(Ⅱ)若每件该商品的成本为4元时,写出厂家销售该商品的年利润万元与售价元之间的关系;
(Ⅲ)当该商品售价为多少元时,使厂家销售该商品所获年利润最大.
22.(本小题满分14分)
已知函数,设。
(Ⅰ)求F(x)的单调区间;
(Ⅱ)若以图象上任意一点为切点的切线的斜率 恒成立,求实数的最小值。
(Ⅲ)是否存在实数,使得函数的图象与的图象恰好有四个不同的交点?若存在,求出的取值范围,若不存在,说明理由。
高三模块检测理科数学卷
参考答案及评分标准
一. 选择题 : (本大题共12小题, 每小题5分, 共60分)
二.填空题: (本大题有4小题, 每小题4分, 共16分)
13. 14. 5 15. 16
解答题: (本大题有6小题, 共74分)
(Ⅱ)依题意得: ……… 8分
由 ……………… 10分
解得 ……………… 11分
故的单调增区间为: ……………… 12分
18解:
(I)设等比数列的公比为.由可得, ………1分
因为,所以 ……………………………………2分
依题有,因为,所以, …………4分
所以数列通项为 ……………………………6分
(II) ……………………………………8分
① ………9分
② …………………10分
①-②得
……………………………………11分
即得 …………………………………12分
20.(1)如图,连接AC,∵ABCD为矩形,且F是BD的中点,∴AC必经过F ……………….2分
又E是PC的中点,
所以,EF∥AP. ……………4分
∵EF在面PAD外,PA在面内
∴EF∥面PAD……………6分
(2)∵面PAD⊥面ABCD,CD⊥AD,面PAD面ABCD=AD,∴CD⊥面PAD,
又AP面PAD,∴AP⊥CD. ……………………8分
又∵AP⊥PD,PD和CD是相交直线,AP⊥面PCD.……………10分
又AP面PAB,所以,面PAB⊥面PDC. ……………………12分
(4,5) 5 (5,7) 7 (7,7.5)
+ 0 - 0 +
增 极大值50 减 极小值2 增
22.解:(Ⅰ) )
…………………………1分
…………2分
由。…………3分
…………4分
(Ⅱ)…5分
…………6分
当…………7分
…………8分
(Ⅲ)若的图象与
的图象恰有四个不同交点,
即有四个不同的根,亦即
有四个不同的根。…………10分
令,
则。
第Ⅰ卷
注意事项:第Ⅰ卷为选择题,共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一个最符合题目要求。每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选择其他答案标号。不能直接写在本试卷上。
选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1已知△ABC中,,则( )
(A) (B) (C) (D)
2.设复数是实数,则实数
( )
A. B. C. D.
3.已知向量,且,则向量与的夹角为 ( )
A.60° B.120° C.135° D.150°
4.若等差数列{an}的前5项和S5=30,且a2=7,则a7 = ( )
A.0 B.1 C.2 D.3
5. 将函数的图象向左平移个单位,再向上平移1个单位,所得图象的函
数解析式是( )
A. B. C. D.
6.函数f(x)=的图象是( )
7.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是( )
A. B. C. D.
8.设f(x)=则f(ln3)= ( )
A. ln3-1 B. C.e D.3e
9. 曲线在点(2, 4)处的切线方程是( )
A. B. C. D.
10.如图,ABCD-A1B1C1D1为正方体,下面结论错误的是 ( )
A.BD∥平面CB1D1 B.AC1⊥BD
C.异面直线与所成的角为 D.AC1⊥平面CB1D1
11.定义在R上的偶函数f(x)在上递增,,则满足>0的x的取值范围是 ( )
A. B. C. D.
12.设函数在内有定义,对于给定的正数K,定义函数
取函数,=时,函数的调递增区间为( )
A . B. C . D .
第Ⅱ卷
注意事项:
第Ⅱ卷共90分。第II卷所有题目的答案考生必须将用黑色签字笔、钢笔或圆珠笔答在规定位置。
二、填空题:(本大题共4小题,每小题4分,共16分.)
13.若,则= .
14.设变量x,y满足约束条件则目标函数的最大值为 .
15.已知直线是曲线的切线,则 .
16.定义在R上的偶函数在[—1,0]上是增函数,给出下列关于的判断;是周期函数;关于直线对称;是[0,1]上是增函数;在[1,2]上是减函数;关于(,0)中心对称;。
其中所有正确的序号是 。
三、解答题:本大题共6小题,共74分.解答应写文字说明,证明过程或演算步骤.
17.(本小题满分12分)
设函数的最小正周期为.
(Ⅰ)求的值.
(Ⅱ)若函数的图像是由的图像向右平移个单位长度得到,求的单调增区间.
18. (本小题满分12分)
在等比数列中,,且,是和的等差中项.
(I)求数列的通项公式;
(II)若数列满足,求数列的前项和.
19. (本小题满分12分)
口袋中装有质地大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸一个球,记下编号,放回后乙再摸一个球,记下编号。如果两个编号的和为偶数就算甲胜,否则算乙胜。
(1)求甲胜且编号和为6的事件发生的概率;
(2)这种游戏规则公平吗?说明理由。
20.(本小题满分12分)
如图,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.
(1)求证:EF∥面PAD;
(2)求证:面PDC⊥面PAB;
21.(本小题满分12分)
某厂家拟对一商品举行促销活动,当该商品的售价为元时,全年的促销费用为万元;根据以往的销售经验,实施促销后的年销售量万件,其中4为常数.当该商品的售价为6元时,年销售量为49万件.
(Ⅰ)求出的值;
(Ⅱ)若每件该商品的成本为4元时,写出厂家销售该商品的年利润万元与售价元之间的关系;
(Ⅲ)当该商品售价为多少元时,使厂家销售该商品所获年利润最大.
22.(本小题满分14分)
已知函数,设。
(Ⅰ)求F(x)的单调区间;
(Ⅱ)若以图象上任意一点为切点的切线的斜率 恒成立,求实数的最小值。
(Ⅲ)是否存在实数,使得函数的图象与的图象恰好有四个不同的交点?若存在,求出的取值范围,若不存在,说明理由。
高三模块检测理科数学卷
参考答案及评分标准
一. 选择题 : (本大题共12小题, 每小题5分, 共60分)
二.填空题: (本大题有4小题, 每小题4分, 共16分)
13. 14. 5 15. 16
解答题: (本大题有6小题, 共74分)
(Ⅱ)依题意得: ……… 8分
由 ……………… 10分
解得 ……………… 11分
故的单调增区间为: ……………… 12分
18解:
(I)设等比数列的公比为.由可得, ………1分
因为,所以 ……………………………………2分
依题有,因为,所以, …………4分
所以数列通项为 ……………………………6分
(II) ……………………………………8分
① ………9分
② …………………10分
①-②得
……………………………………11分
即得 …………………………………12分
20.(1)如图,连接AC,∵ABCD为矩形,且F是BD的中点,∴AC必经过F ……………….2分
又E是PC的中点,
所以,EF∥AP. ……………4分
∵EF在面PAD外,PA在面内
∴EF∥面PAD……………6分
(2)∵面PAD⊥面ABCD,CD⊥AD,面PAD面ABCD=AD,∴CD⊥面PAD,
又AP面PAD,∴AP⊥CD. ……………………8分
又∵AP⊥PD,PD和CD是相交直线,AP⊥面PCD.……………10分
又AP面PAB,所以,面PAB⊥面PDC. ……………………12分
(4,5) 5 (5,7) 7 (7,7.5)
+ 0 - 0 +
增 极大值50 减 极小值2 增
22.解:(Ⅰ) )
…………………………1分
…………2分
由。…………3分
…………4分
(Ⅱ)…5分
…………6分
当…………7分
…………8分
(Ⅲ)若的图象与
的图象恰有四个不同交点,
即有四个不同的根,亦即
有四个不同的根。…………10分
令,
则。
同课章节目录
