2 万有引力定律同步课件 25张PPT
文档属性
| 名称 | 2 万有引力定律同步课件 25张PPT |  | |
| 格式 | ppt | ||
| 文件大小 | 788.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-01 20:08:14 | ||
图片预览








文档简介
(共25张PPT)
习题课二 万有引力定律的应用
关键能力·探究学习
知识点一 天体运动各物理量与轨道半径关系的定性分析
《今日宇宙》网站统计,正在地球周围工作的卫星有1
071颗,其中约500颗为近地轨道卫星,50颗为中轨道卫星(20
000
km),其余为地球同步静止轨道卫星(36
000
km),这么多不同轨道的卫星的线速度大小,角速度,周期,向心加速度大小与什么因素有关?
提示:与轨道半径有关。
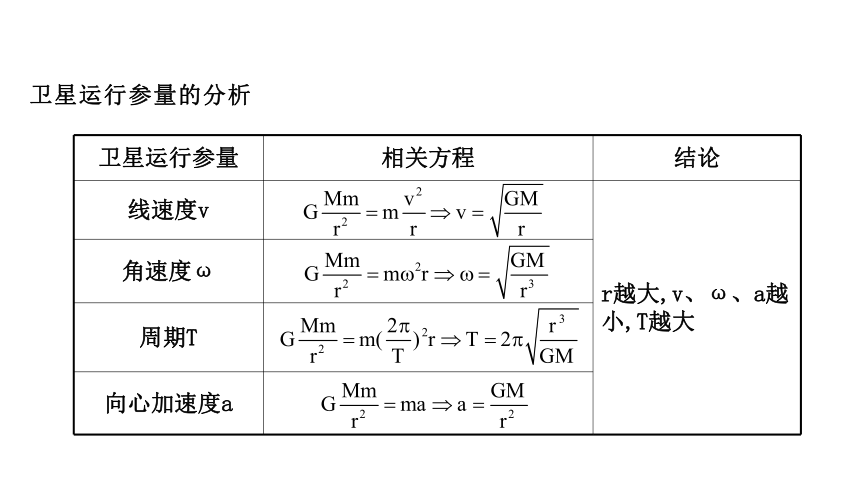
卫星运行参量的分析
卫星运行参量
相关方程
结论
线速度v
r越大,v、ω、a越小,T越大
角速度ω
周期T
向心加速度a
提醒:地面上随地球自转的物体不适用此结论。
【典例示范】
【典例】(多选)(2020·江苏高考)甲、乙两颗人造卫星质量相等,均绕地球做
圆周运动,甲的轨道半径是乙的2倍。下列应用公式进行的推论正确的有
( )
A.由v=
可知,甲的速度是乙的
倍
B.由a=ω2r可知,甲的向心加速度是乙的2倍
C.由F=G
可知,甲的向心力是乙的
D.由
可知,甲的周期是乙的2
倍
【解析】选C、D。卫星绕地球做圆周运动,万有引力提供向心力,则F向=
卫星的运行线速度
代入数据可得
故A错误;因为在不同轨道上两卫星的角速度、轨道半径都不一样,故不能
根据a=ω2r分析两卫星加速度的关系,卫星的运行加速度a=
代入数据可得
故B错误;根据F向=
两颗人造卫星质量相等,可得
故C正确;两卫星均绕地球做圆周运动,根据开普勒第三定律
可得
故D正确。
【题后反思】
求解卫星问题必须抓住卫星运动特点:万有引力提供绕地球做圆周运动的向
心力,由方程
求出相应物理量的表达式即可
求解,需要注意an、v、ω、T均与卫星的质量无关。
【素养训练】
两颗卫星都围绕地球做匀速圆周运动,卫星A轨道半径为36
000
km,卫星B轨道半径为21
500
km。下列说法正确的是
( )
A.两颗卫星的发射速度均小于第一宇宙速度
B.卫星A的速率比卫星B的大
C.卫星A的向心加速度小于卫星B的向心加速度
D.卫星A的运动周期小于卫星B的运动周期
【解析】选C。第一宇宙速度是最小的发射速度,由于两颗卫星的轨道高度都较大,
所以两颗卫星的发射速度均大于第一宇宙速度,故A错误;根据人造卫星的万有引力
等于向心力,得:
可得:
可知卫星的轨道半径越小,角速度、线速度、向心加速度越大,周期越小,由题中A
的轨道半径大于B的轨道半径,则知A周期大,A的速度和向心加速度都小,故C正
确,B、D错误。
知识点二 双星模型
1.定义:绕公共圆心转动的两个星体组成的系统,我们称之为双星系统,如图所示。
2.特点:
(1)各自所需的向心力由彼此间的万有引力相互提供,即
(2)两颗星的周期及角速度都相同,即T1=T2,ω1=ω2
(3)两颗星的半径与它们之间的距离关系为:r1+r2=L
3.两颗星到圆心的距离r1、r2与星体质量成反比,即
与星体运动的线速
度成正比。
【问题探究】
宇宙中靠得很近的两个天体可以构成“双星系统”,以它们连线上的一点为圆心,做匀速圆周运动,两天体及圆心始终在同一直线上。“双星系统”做圆周运动所需的向心力是什么力提供?它们的周期有什么关系?
提示:两天体之间的万有引力提供向心力。两天体周期相同。
【典例示范】
【典例】(2020·大连高一检测)两个质量不同的天体构成双星系统,它们以二者连线上的某一点为圆心做匀速圆周运动,下列说法正确的是
( )
A.质量大的天体线速度较大
B.质量小的天体角速度较大
C.两个天体的向心力大小一定相等
D.两个天体的向心加速度大小一定相等
【解析】选C。双星系统的结构是稳定的,故它们的角速度大小相等,故B项错误;
两个星球间的万有引力提供向心力,根据牛顿第三定律可知,两个天体的向心力
大小相等,而天体质量不一定相等,故两个天体的向心加速度大小不一定相等,
故C项正确,D错误;根据牛顿第二定律,有:G
=m1ω2r1=m2ω2r2,其
中:r1+r2=L,故r1=
L,r2=
L,故
故质量大的天体线速度
较小,故A错误。
【素养训练】
1.(多选)甲、乙两星组成双星系统,它们离其他天体都很遥远;观察到它们的距离始终为L,甲的轨道半径为R,运行周期为T。下列说法正确的是
( )
A.乙星的质量大小为
B.乙星的向心加速度大小为
C.若两星的距离减小,则它们的运行周期会变小
D.甲、乙两星的质量之比为
【解析】选A、C。对双星系统的两颗星球,由它们之间的万有引力提供向心力:
可得:m乙=
故A正确;乙的轨道半径:r=L-R,则乙的向心
加速度:
故B错误。若两星的距离减小,根据
得
则它们的运行周期会变
小,故C正确。双星系统具有相等的角速度和周期,由它们之间的万有引力提供
向心力,得:
所以:Rm甲=(L-R)·m乙,甲、乙两
星的质量之比为
,故D错误。
2.(多选)(2020·德州高一检测)宇宙中两颗相距很近的恒星常常组成一个双星系统。它们以相互间的万有引力彼此提供向心力,从而使它们绕着某一共同的圆心做匀速圆周运动,若已知某双星系统的运转周期为T,两星到共同圆心的距离分别为R1和R2,引力常量为G,那么下列说法正确的是
( )
A.这两颗恒星的质量必定相等
B.这两颗恒星的质量之和为
C.这两颗恒星的质量之比m1∶m2=R2∶R1
D.其中必有一颗恒星的质量为
【解析】选B、C、D。两星有共同的周期T,由牛顿第二定律得
所以两星的质量之比m1∶m2=R2∶R1,故C正确;由上式可得
故A错误,B、C、
D正确。
1.(2020·天津等级考)北斗问天,国之夙愿。我国北斗三号系统的收官之星是地球静止轨道卫星,其轨道半径约为地球半径的7倍。与近地轨道卫星相比,地球静止轨道卫星( )
A.周期大
B.线速度大
C.角速度大
D.加速度大
课堂检测·素养达标
【解析】选A。根据天体环绕的“高轨、低速、长周期”可知,地球静止轨道卫
星的轨道半径高于近地卫星,所以线速度和角速度均小于近地卫星,周期长于近
地卫星,故A正确,B、C错误。由
可知,加速度与轨道半径的平方成反
比,地球静止轨道卫星的加速度小于近地卫星的加速度,故D错误。
2.(多选)2019年8月17日,“捷龙一号”首飞成功,标志着中国“龙”系列商业运载火箭从此登上历史舞台。“捷龙一号”在发射卫星时,首先将该卫星发射到低空圆轨道1,待测试正常后通过变轨进入高空圆轨道2。假设卫星的质量不变,在两轨道上运行时的速率之比v1∶v2=3∶2,则
( )
A.卫星在两轨道运行时的向心加速度大小之比a1∶a2
=81∶16
B.卫星在两轨道运行时的角速度大小之比ω1∶ω2
=25∶4
C.卫星在两轨道运行的周期之比T1∶T2=4∶27
D.卫星在两轨道运行时的动能之比Ek1∶Ek2
=9∶4
【解析】选A、D。根据
可得v=
,因为v1∶v2=3∶2,则
r1∶r2=4∶9。根据
可知:a=
,可得卫星
在两轨道运行时的向心加速度大小之比a1∶a2
=81∶16,选项A正确;由ω=
可得,卫星在两轨道运行时的角速度大小之比ω1∶ω2
=27∶8,选项B错误;
由
可知,卫星在两轨道运行的周期之比T1
∶T2=8∶27,选项C错误;根据
则卫星在两轨道运行时的动能之比Ek1∶Ek2
=9∶4,选项D正确。
3.如图所示,两颗星球组成的双星,在相互之间的万有引力作用下,绕其连线上的O点做周期相同的匀速圆周运动。现测得两颗星之间的距离为L,质量之比为m1∶m2=3∶2,下列说法中正确的是
( )
A.m1、m2做圆周运动的线速度之比为3∶2
B.m1、m2做圆周运动的角速度之比为3∶2
C.m1做圆周运动的半径为
L
D.m2做圆周运动的半径为
L
【解析】选C。设双星m1、m2距转动中心O的距离分别为r1、r2,双星绕O点转动的
角速度均为ω,据万有引力定律得
=m1r1ω2=m2r2ω2,又r1+r2=L,m1∶m2=3∶2,
所以可解得r1=
L,r2=
L
。m1、m2运动的线速度分别为v1=r1ω,v2=r2ω,故
v1∶v2=r1∶r2=2∶3。综上所述,选项C正确。
习题课二 万有引力定律的应用
关键能力·探究学习
知识点一 天体运动各物理量与轨道半径关系的定性分析
《今日宇宙》网站统计,正在地球周围工作的卫星有1
071颗,其中约500颗为近地轨道卫星,50颗为中轨道卫星(20
000
km),其余为地球同步静止轨道卫星(36
000
km),这么多不同轨道的卫星的线速度大小,角速度,周期,向心加速度大小与什么因素有关?
提示:与轨道半径有关。
卫星运行参量的分析
卫星运行参量
相关方程
结论
线速度v
r越大,v、ω、a越小,T越大
角速度ω
周期T
向心加速度a
提醒:地面上随地球自转的物体不适用此结论。
【典例示范】
【典例】(多选)(2020·江苏高考)甲、乙两颗人造卫星质量相等,均绕地球做
圆周运动,甲的轨道半径是乙的2倍。下列应用公式进行的推论正确的有
( )
A.由v=
可知,甲的速度是乙的
倍
B.由a=ω2r可知,甲的向心加速度是乙的2倍
C.由F=G
可知,甲的向心力是乙的
D.由
可知,甲的周期是乙的2
倍
【解析】选C、D。卫星绕地球做圆周运动,万有引力提供向心力,则F向=
卫星的运行线速度
代入数据可得
故A错误;因为在不同轨道上两卫星的角速度、轨道半径都不一样,故不能
根据a=ω2r分析两卫星加速度的关系,卫星的运行加速度a=
代入数据可得
故B错误;根据F向=
两颗人造卫星质量相等,可得
故C正确;两卫星均绕地球做圆周运动,根据开普勒第三定律
可得
故D正确。
【题后反思】
求解卫星问题必须抓住卫星运动特点:万有引力提供绕地球做圆周运动的向
心力,由方程
求出相应物理量的表达式即可
求解,需要注意an、v、ω、T均与卫星的质量无关。
【素养训练】
两颗卫星都围绕地球做匀速圆周运动,卫星A轨道半径为36
000
km,卫星B轨道半径为21
500
km。下列说法正确的是
( )
A.两颗卫星的发射速度均小于第一宇宙速度
B.卫星A的速率比卫星B的大
C.卫星A的向心加速度小于卫星B的向心加速度
D.卫星A的运动周期小于卫星B的运动周期
【解析】选C。第一宇宙速度是最小的发射速度,由于两颗卫星的轨道高度都较大,
所以两颗卫星的发射速度均大于第一宇宙速度,故A错误;根据人造卫星的万有引力
等于向心力,得:
可得:
可知卫星的轨道半径越小,角速度、线速度、向心加速度越大,周期越小,由题中A
的轨道半径大于B的轨道半径,则知A周期大,A的速度和向心加速度都小,故C正
确,B、D错误。
知识点二 双星模型
1.定义:绕公共圆心转动的两个星体组成的系统,我们称之为双星系统,如图所示。
2.特点:
(1)各自所需的向心力由彼此间的万有引力相互提供,即
(2)两颗星的周期及角速度都相同,即T1=T2,ω1=ω2
(3)两颗星的半径与它们之间的距离关系为:r1+r2=L
3.两颗星到圆心的距离r1、r2与星体质量成反比,即
与星体运动的线速
度成正比。
【问题探究】
宇宙中靠得很近的两个天体可以构成“双星系统”,以它们连线上的一点为圆心,做匀速圆周运动,两天体及圆心始终在同一直线上。“双星系统”做圆周运动所需的向心力是什么力提供?它们的周期有什么关系?
提示:两天体之间的万有引力提供向心力。两天体周期相同。
【典例示范】
【典例】(2020·大连高一检测)两个质量不同的天体构成双星系统,它们以二者连线上的某一点为圆心做匀速圆周运动,下列说法正确的是
( )
A.质量大的天体线速度较大
B.质量小的天体角速度较大
C.两个天体的向心力大小一定相等
D.两个天体的向心加速度大小一定相等
【解析】选C。双星系统的结构是稳定的,故它们的角速度大小相等,故B项错误;
两个星球间的万有引力提供向心力,根据牛顿第三定律可知,两个天体的向心力
大小相等,而天体质量不一定相等,故两个天体的向心加速度大小不一定相等,
故C项正确,D错误;根据牛顿第二定律,有:G
=m1ω2r1=m2ω2r2,其
中:r1+r2=L,故r1=
L,r2=
L,故
故质量大的天体线速度
较小,故A错误。
【素养训练】
1.(多选)甲、乙两星组成双星系统,它们离其他天体都很遥远;观察到它们的距离始终为L,甲的轨道半径为R,运行周期为T。下列说法正确的是
( )
A.乙星的质量大小为
B.乙星的向心加速度大小为
C.若两星的距离减小,则它们的运行周期会变小
D.甲、乙两星的质量之比为
【解析】选A、C。对双星系统的两颗星球,由它们之间的万有引力提供向心力:
可得:m乙=
故A正确;乙的轨道半径:r=L-R,则乙的向心
加速度:
故B错误。若两星的距离减小,根据
得
则它们的运行周期会变
小,故C正确。双星系统具有相等的角速度和周期,由它们之间的万有引力提供
向心力,得:
所以:Rm甲=(L-R)·m乙,甲、乙两
星的质量之比为
,故D错误。
2.(多选)(2020·德州高一检测)宇宙中两颗相距很近的恒星常常组成一个双星系统。它们以相互间的万有引力彼此提供向心力,从而使它们绕着某一共同的圆心做匀速圆周运动,若已知某双星系统的运转周期为T,两星到共同圆心的距离分别为R1和R2,引力常量为G,那么下列说法正确的是
( )
A.这两颗恒星的质量必定相等
B.这两颗恒星的质量之和为
C.这两颗恒星的质量之比m1∶m2=R2∶R1
D.其中必有一颗恒星的质量为
【解析】选B、C、D。两星有共同的周期T,由牛顿第二定律得
所以两星的质量之比m1∶m2=R2∶R1,故C正确;由上式可得
故A错误,B、C、
D正确。
1.(2020·天津等级考)北斗问天,国之夙愿。我国北斗三号系统的收官之星是地球静止轨道卫星,其轨道半径约为地球半径的7倍。与近地轨道卫星相比,地球静止轨道卫星( )
A.周期大
B.线速度大
C.角速度大
D.加速度大
课堂检测·素养达标
【解析】选A。根据天体环绕的“高轨、低速、长周期”可知,地球静止轨道卫
星的轨道半径高于近地卫星,所以线速度和角速度均小于近地卫星,周期长于近
地卫星,故A正确,B、C错误。由
可知,加速度与轨道半径的平方成反
比,地球静止轨道卫星的加速度小于近地卫星的加速度,故D错误。
2.(多选)2019年8月17日,“捷龙一号”首飞成功,标志着中国“龙”系列商业运载火箭从此登上历史舞台。“捷龙一号”在发射卫星时,首先将该卫星发射到低空圆轨道1,待测试正常后通过变轨进入高空圆轨道2。假设卫星的质量不变,在两轨道上运行时的速率之比v1∶v2=3∶2,则
( )
A.卫星在两轨道运行时的向心加速度大小之比a1∶a2
=81∶16
B.卫星在两轨道运行时的角速度大小之比ω1∶ω2
=25∶4
C.卫星在两轨道运行的周期之比T1∶T2=4∶27
D.卫星在两轨道运行时的动能之比Ek1∶Ek2
=9∶4
【解析】选A、D。根据
可得v=
,因为v1∶v2=3∶2,则
r1∶r2=4∶9。根据
可知:a=
,可得卫星
在两轨道运行时的向心加速度大小之比a1∶a2
=81∶16,选项A正确;由ω=
可得,卫星在两轨道运行时的角速度大小之比ω1∶ω2
=27∶8,选项B错误;
由
可知,卫星在两轨道运行的周期之比T1
∶T2=8∶27,选项C错误;根据
则卫星在两轨道运行时的动能之比Ek1∶Ek2
=9∶4,选项D正确。
3.如图所示,两颗星球组成的双星,在相互之间的万有引力作用下,绕其连线上的O点做周期相同的匀速圆周运动。现测得两颗星之间的距离为L,质量之比为m1∶m2=3∶2,下列说法中正确的是
( )
A.m1、m2做圆周运动的线速度之比为3∶2
B.m1、m2做圆周运动的角速度之比为3∶2
C.m1做圆周运动的半径为
L
D.m2做圆周运动的半径为
L
【解析】选C。设双星m1、m2距转动中心O的距离分别为r1、r2,双星绕O点转动的
角速度均为ω,据万有引力定律得
=m1r1ω2=m2r2ω2,又r1+r2=L,m1∶m2=3∶2,
所以可解得r1=
L,r2=
L
。m1、m2运动的线速度分别为v1=r1ω,v2=r2ω,故
v1∶v2=r1∶r2=2∶3。综上所述,选项C正确。
