1 曲线运动的典型问题 同步课件(共36张PPT)
文档属性
| 名称 | 1 曲线运动的典型问题 同步课件(共36张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 959.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-01 20:15:13 | ||
图片预览











文档简介
(共36张PPT)
习题课一 曲线运动的典型问题
关键能力·探究学习
知识点一 小船渡河问题
1.三个速度:
(1)分速度v水:水流的速度;
(2)分速度v船:船在静水中的速度;
(3)合速度v:表示船的实际航行的速度。
2.两类问题三种情景:
渡河
时间
最短
当船头方向垂直于河岸时,渡河时
间最短,最短时间t
min=
渡河
位移
最短
如果v船>v水,当船头方向与上游夹角θ
满足v船cos
θ=v水时,合速度垂直于河
岸,渡河位移最短,等于河宽d
如果v船合速度方向垂直时,渡河位移最短,等
于
【问题探究】
若人在河中始终保持头朝正前方游向对岸,你认为他会到达正对岸,还是会偏向
上游或下游?
提示:不会到达正对岸,会偏向下游。
【典例示范】
【典例】一小船渡河,河宽d=180
m,水流速度v1=2.5
m/s,船在静水中的速度为v2=5
m/s,则:
(1)欲使船在最短的时间内渡河,船头应朝什么方向?用多长时间?位移是多大?
(2)欲使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多大?
(3)如果其他条件不变,水流速度变为6
m/s。船过河的最短时间和最小位移是多大?
【解题探究】
(1)小船渡河时同时参与了几个分运动?如何渡河时间最短?
提示:参与了两个分运动,一个是船相对水的运动(即船在静水中的运动),一个是船随水漂流的运动(即水的运动)。当v船垂直于河岸时到达对岸用时最短,最短时间与v水无关。
(2)当v水v船时,分别怎样渡河位移最小?
提示:当v水v船
时,
v水v船d短航程,当v船与v合垂直时,航程最短,最小位移为xmin=
d。
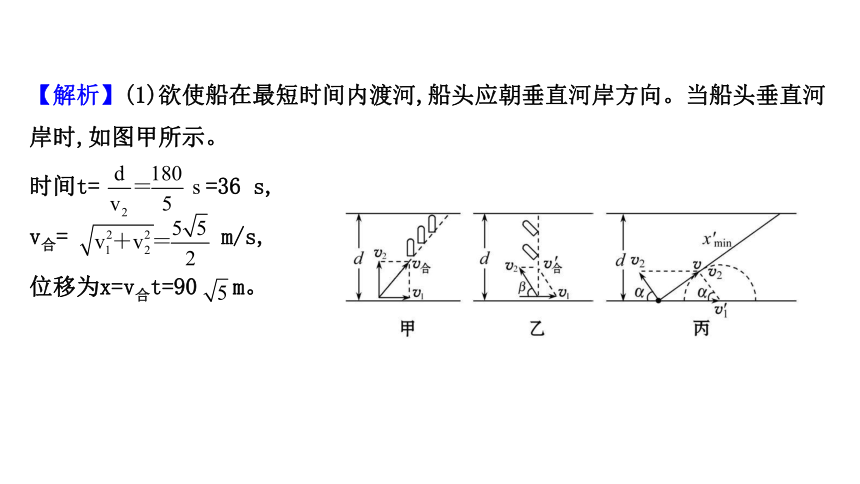
【解析】(1)欲使船在最短时间内渡河,船头应朝垂直河岸方向。当船头垂直河
岸时,如图甲所示。
时间t=
=36
s,
v合=
m/s,
位移为x=v合t=90
m。
(2)欲使船渡河航程最短,应使合运动的速度方向垂直河岸,船头应朝上游与河
岸成某一夹角β,如图乙所示,有v2cosβ=v1,得β=60°。
最小位移为xmin=d=180
m,
所用时间
(3)最短渡河时间只与v2有关,与v1无关,当船头垂直于河岸渡河时时间最短,
t=
=36
s。
当水流速度变为6
m/s时,即v1'>v2,则合速度不可能垂直于河岸,无法垂直渡河。
如图丙所示,以v1'矢量的末端为圆心、以矢量v2的大小为半径画弧,从v1'矢量
的始端向圆弧作切线,则合速度沿此切线方向时航程最短,设船头与上游河岸夹
角为α,则cosα=
,最小位移为
xmin'=
=216
m。
答案:(1)船头垂直于河岸 36
s 90
m
(2)船头偏向上游,与河岸夹角为60° 24
s 180
m
(3)36
s 216
m
【题后反思】小船渡河问题的分析思路
【素养训练】
1.(多选)下列图中实线为河岸,河水的流动方向如图中v的箭头所示,虚线为小船从河岸M驶向对岸N的实际航线。则其中可能正确的是
( )
【解析】选A、B。小船渡河的运动可看作水流的运动和小船运动的合运动。虚线为小船从河岸M驶向对岸N的实际航线,即合速度的方向,小船合运动的速度方向就是其实际运动的方向,分析可知,实际航线可能正确的是A、B。
2.小船在水速较小的河中横渡,并使船头始终垂直河岸航行,到达河中间时突然上游来水使水流速度加快,则对此小船渡河的说法正确的是
( )
A.小船要用更长的时间才能到达对岸
B.小船到达对岸的时间不变,但位移将变大
C.因小船船头始终垂直河岸航行,故所用时间及位移都不会变化
D.因船速与水速关系未知,故无法确定渡河时间及位移的变化
【解析】选B。因为小船船头垂直于河岸,则渡河时间t=
,水流速增大,渡河
时间不变,沿河岸方向的位移增大,则最终渡河的位移变大,故B正确,A、D错误;
因小船船头始终垂直河岸航行,渡河时间不会随着水流速度增大而变化,故C错
误。
知识点二 关联速度问题
1.关联速度问题特点:
(1)绳(杆)物关联问题:两物体通过绳(杆)相牵连,当两物体都发生运动时,两物体的速度往往不相等,但因绳(杆)的长度是不变的,因此两物体的速度沿绳(杆)方向的分速度大小是相等的。
(2)杆点(面)关联问题:杆的一端和一个物体的某点(面)接触,两物体通过绳(杆)相牵连,当两物体都发生运动时,两物体的速度往往不相等,但因二者始终接触,因此两物体的速度沿垂直接触面方向的分速度大小是相等的。
2.常见模型:
【问题探究】
汽车在水平地面上向左匀速运动,利用绕过定滑轮的绳子吊起某物体竖直上升。
(1)物体竖直向上做的是匀速直线运动吗?
提示:物体的速度v2=v1cosθ,因为θ减小,所以物体的速度增大,物体做加速运动。
(2)物体所受的拉力和重力大小的关系?
提示:由于物体做加速运动,所以拉力大于重力。
【典例示范】
【典例】(2020·东营高一检测)质量为m的物体P置于倾角为θ1的固定光滑斜面上,轻细绳跨过光滑定滑轮分别连接着P与小车,P与滑轮间的细绳平行于斜面,小车以速率v水平向右做匀速直线运动。如图,当小车与滑轮间的细绳和水平方向成夹角θ2时,下列判断正确的是
( )
A.P的速率为v
B.P的速率为vcosθ2
C.绳的拉力等于mgsinθ1
D.绳的拉力小于mgsinθ1
【解析】选B。将小车的速度v进行分解如图所示,则有:vP=vcosθ2,故A错误,B正确;小车向右运动,θ2减小,v不变,则vP逐渐增大,说明物体P沿斜面向上做加速运动,由牛顿第二定律有:T-mgsinθ1=ma,可知绳对A的拉力为:T>mgsinθ1,故C、D错误。
【题后反思】分析“关联”速度的基本步骤
【素养训练】
1.(2020·济宁高一检测)在水平地面上做匀速直线运动的小车,通过定滑轮用绳子吊起一个物体,若小车和被吊的物体在同一时刻速度分别为v1和v2,绳子对物体的拉力为FT,物体所受重力为G,则下面说法正确的是
( )
A.物体做匀速运动,且
v1=v2
B.物体做加速运动,且v2C.物体做加速运动
,且
FT=G
D.物体做匀速运动,且FT=G
【解析】选B。小车的运动可分解为沿绳子方向和垂直绳子的方向两个运动,设两段绳子的夹角为θ,由几何知识可得v2=v1sinθ,所以v2G,故选项C、D错误。
2.如图,A、B两物体系在跨过光滑定滑轮的一根轻绳的两端,若A物体以速度v沿水平地面向左运动,某时刻系A、B的绳分别与水平方向成α、β角,求此时B物体的速度。
【解析】A、B两物体速度分解图如图所示,由于两物体沿绳的速度分量相等,所
以有v1=
即vcosα=vBcosβ,
解得vB=
v,方向水平向右。
答案:
v,方向水平向右
1.一摩托艇要到正对岸抢救物资,关于该摩托艇能否到达正对岸的说法中正确的是
( )
A.只要摩托艇向正对岸行驶就能到达正对岸
B.由于水流有较大的速度,摩托艇不能到达正对岸
C.虽然水流有较大的速度,但只要摩托艇向上游某一方向行驶,一定能到达正对岸
D.有可能不论摩托艇怎么行驶,都不能到达正对岸
课堂检测·素养达标
【解析】选D。若摩托艇在静水中的速度大于水流的速度,只要方向朝水流的上游,找一个合适的角度使摩托艇沿河岸的速度等于水流的速度,就能到达正对岸,若摩托艇在静水中的速度小于水流的速度,无论朝哪个方向开,都不会到达正对岸,只能到达对岸的下游某个地方,故选项D正确,A、B、C错误。
2.(多选)某河宽为600
m,河中某点的水流速度v与该点到较近河岸的距离d的关
系图像如图所示,现船以静水中的速度4
m/s
渡河,且船渡河的时间最短,下列
说法正确的是
( )
A.船在河水中航行的轨迹是一条直线
B.船在行驶过程中,船头始终与河岸垂直
C.船离开河岸400
m时的速度大小为2
m/s
D.渡河最短时间为240
s
【解析】选B、C。因为静水速不变,水流速在变化,知沿河岸方向上有加速度,
合速度的方向与加速度的方向不在同一条直线上,知轨迹是曲线,故选项A错误;
当静水速与河岸垂直时,渡河时间最短,t=
s=150
s,故选项B正确,D错
误;船离开河岸400
m时,离河岸较近的距离为200
m,此时水流速度为2
m/s。根
据平行四边形定则v=
m/s=2
m/s,故选项C正确。
3.光滑半球A放在竖直面光滑的墙角,并用手推着保持静止。现在A与墙壁之间放入光滑球B,放手让A和B由静止开始运动,当A、B运动到图示位置时,二者球心的连线与水平面成θ角,速度大小分别为vA和vB,则以下关系正确的是( )
A.vA=vB
B.vA=vBsinθ
C.vA=vBcosθ
D.vA=vBtanθ
【解析】选D。将A、B两球的速度沿两球心的连线和垂直两球心连线分解,如图,由关联速度的关系可得:vAsinθ=vBcosθ,解得:vA=vBtanθ,故D正确。
4.(2020·上饶高一检测)一艘小艇从河岸A处出发渡河,小艇保持与河岸垂直方向行驶,经过10
min到达正对岸下游120
m的C处,如图所示,如果小艇保持原来的速度逆水斜向上游与河岸成α角方向行驶,则经过12.5
min恰好到达正对岸的B处,求:河的宽度。
【解析】设河宽为d,河水流速为v1,船速大小为v2,船两次运动速度合成如图所示。
依题意有:v2t1=v2sinα·t2
BC的距离为:
=v1t1
速度关系为:
=cosα
联立可得:v1=12
m/min
由上可得:sinα=0.8,故cosα=0.6,
河宽:d=v2t1=
×10
m=200
m。
答案:200
m
习题课一 曲线运动的典型问题
关键能力·探究学习
知识点一 小船渡河问题
1.三个速度:
(1)分速度v水:水流的速度;
(2)分速度v船:船在静水中的速度;
(3)合速度v:表示船的实际航行的速度。
2.两类问题三种情景:
渡河
时间
最短
当船头方向垂直于河岸时,渡河时
间最短,最短时间t
min=
渡河
位移
最短
如果v船>v水,当船头方向与上游夹角θ
满足v船cos
θ=v水时,合速度垂直于河
岸,渡河位移最短,等于河宽d
如果v船
于
【问题探究】
若人在河中始终保持头朝正前方游向对岸,你认为他会到达正对岸,还是会偏向
上游或下游?
提示:不会到达正对岸,会偏向下游。
【典例示范】
【典例】一小船渡河,河宽d=180
m,水流速度v1=2.5
m/s,船在静水中的速度为v2=5
m/s,则:
(1)欲使船在最短的时间内渡河,船头应朝什么方向?用多长时间?位移是多大?
(2)欲使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多大?
(3)如果其他条件不变,水流速度变为6
m/s。船过河的最短时间和最小位移是多大?
【解题探究】
(1)小船渡河时同时参与了几个分运动?如何渡河时间最短?
提示:参与了两个分运动,一个是船相对水的运动(即船在静水中的运动),一个是船随水漂流的运动(即水的运动)。当v船垂直于河岸时到达对岸用时最短,最短时间与v水无关。
(2)当v水
提示:当v水
时,
v水v船d短航程,当v船与v合垂直时,航程最短,最小位移为xmin=
d。
【解析】(1)欲使船在最短时间内渡河,船头应朝垂直河岸方向。当船头垂直河
岸时,如图甲所示。
时间t=
=36
s,
v合=
m/s,
位移为x=v合t=90
m。
(2)欲使船渡河航程最短,应使合运动的速度方向垂直河岸,船头应朝上游与河
岸成某一夹角β,如图乙所示,有v2cosβ=v1,得β=60°。
最小位移为xmin=d=180
m,
所用时间
(3)最短渡河时间只与v2有关,与v1无关,当船头垂直于河岸渡河时时间最短,
t=
=36
s。
当水流速度变为6
m/s时,即v1'>v2,则合速度不可能垂直于河岸,无法垂直渡河。
如图丙所示,以v1'矢量的末端为圆心、以矢量v2的大小为半径画弧,从v1'矢量
的始端向圆弧作切线,则合速度沿此切线方向时航程最短,设船头与上游河岸夹
角为α,则cosα=
,最小位移为
xmin'=
=216
m。
答案:(1)船头垂直于河岸 36
s 90
m
(2)船头偏向上游,与河岸夹角为60° 24
s 180
m
(3)36
s 216
m
【题后反思】小船渡河问题的分析思路
【素养训练】
1.(多选)下列图中实线为河岸,河水的流动方向如图中v的箭头所示,虚线为小船从河岸M驶向对岸N的实际航线。则其中可能正确的是
( )
【解析】选A、B。小船渡河的运动可看作水流的运动和小船运动的合运动。虚线为小船从河岸M驶向对岸N的实际航线,即合速度的方向,小船合运动的速度方向就是其实际运动的方向,分析可知,实际航线可能正确的是A、B。
2.小船在水速较小的河中横渡,并使船头始终垂直河岸航行,到达河中间时突然上游来水使水流速度加快,则对此小船渡河的说法正确的是
( )
A.小船要用更长的时间才能到达对岸
B.小船到达对岸的时间不变,但位移将变大
C.因小船船头始终垂直河岸航行,故所用时间及位移都不会变化
D.因船速与水速关系未知,故无法确定渡河时间及位移的变化
【解析】选B。因为小船船头垂直于河岸,则渡河时间t=
,水流速增大,渡河
时间不变,沿河岸方向的位移增大,则最终渡河的位移变大,故B正确,A、D错误;
因小船船头始终垂直河岸航行,渡河时间不会随着水流速度增大而变化,故C错
误。
知识点二 关联速度问题
1.关联速度问题特点:
(1)绳(杆)物关联问题:两物体通过绳(杆)相牵连,当两物体都发生运动时,两物体的速度往往不相等,但因绳(杆)的长度是不变的,因此两物体的速度沿绳(杆)方向的分速度大小是相等的。
(2)杆点(面)关联问题:杆的一端和一个物体的某点(面)接触,两物体通过绳(杆)相牵连,当两物体都发生运动时,两物体的速度往往不相等,但因二者始终接触,因此两物体的速度沿垂直接触面方向的分速度大小是相等的。
2.常见模型:
【问题探究】
汽车在水平地面上向左匀速运动,利用绕过定滑轮的绳子吊起某物体竖直上升。
(1)物体竖直向上做的是匀速直线运动吗?
提示:物体的速度v2=v1cosθ,因为θ减小,所以物体的速度增大,物体做加速运动。
(2)物体所受的拉力和重力大小的关系?
提示:由于物体做加速运动,所以拉力大于重力。
【典例示范】
【典例】(2020·东营高一检测)质量为m的物体P置于倾角为θ1的固定光滑斜面上,轻细绳跨过光滑定滑轮分别连接着P与小车,P与滑轮间的细绳平行于斜面,小车以速率v水平向右做匀速直线运动。如图,当小车与滑轮间的细绳和水平方向成夹角θ2时,下列判断正确的是
( )
A.P的速率为v
B.P的速率为vcosθ2
C.绳的拉力等于mgsinθ1
D.绳的拉力小于mgsinθ1
【解析】选B。将小车的速度v进行分解如图所示,则有:vP=vcosθ2,故A错误,B正确;小车向右运动,θ2减小,v不变,则vP逐渐增大,说明物体P沿斜面向上做加速运动,由牛顿第二定律有:T-mgsinθ1=ma,可知绳对A的拉力为:T>mgsinθ1,故C、D错误。
【题后反思】分析“关联”速度的基本步骤
【素养训练】
1.(2020·济宁高一检测)在水平地面上做匀速直线运动的小车,通过定滑轮用绳子吊起一个物体,若小车和被吊的物体在同一时刻速度分别为v1和v2,绳子对物体的拉力为FT,物体所受重力为G,则下面说法正确的是
( )
A.物体做匀速运动,且
v1=v2
B.物体做加速运动,且v2
,且
FT=G
D.物体做匀速运动,且FT=G
【解析】选B。小车的运动可分解为沿绳子方向和垂直绳子的方向两个运动,设两段绳子的夹角为θ,由几何知识可得v2=v1sinθ,所以v2
2.如图,A、B两物体系在跨过光滑定滑轮的一根轻绳的两端,若A物体以速度v沿水平地面向左运动,某时刻系A、B的绳分别与水平方向成α、β角,求此时B物体的速度。
【解析】A、B两物体速度分解图如图所示,由于两物体沿绳的速度分量相等,所
以有v1=
即vcosα=vBcosβ,
解得vB=
v,方向水平向右。
答案:
v,方向水平向右
1.一摩托艇要到正对岸抢救物资,关于该摩托艇能否到达正对岸的说法中正确的是
( )
A.只要摩托艇向正对岸行驶就能到达正对岸
B.由于水流有较大的速度,摩托艇不能到达正对岸
C.虽然水流有较大的速度,但只要摩托艇向上游某一方向行驶,一定能到达正对岸
D.有可能不论摩托艇怎么行驶,都不能到达正对岸
课堂检测·素养达标
【解析】选D。若摩托艇在静水中的速度大于水流的速度,只要方向朝水流的上游,找一个合适的角度使摩托艇沿河岸的速度等于水流的速度,就能到达正对岸,若摩托艇在静水中的速度小于水流的速度,无论朝哪个方向开,都不会到达正对岸,只能到达对岸的下游某个地方,故选项D正确,A、B、C错误。
2.(多选)某河宽为600
m,河中某点的水流速度v与该点到较近河岸的距离d的关
系图像如图所示,现船以静水中的速度4
m/s
渡河,且船渡河的时间最短,下列
说法正确的是
( )
A.船在河水中航行的轨迹是一条直线
B.船在行驶过程中,船头始终与河岸垂直
C.船离开河岸400
m时的速度大小为2
m/s
D.渡河最短时间为240
s
【解析】选B、C。因为静水速不变,水流速在变化,知沿河岸方向上有加速度,
合速度的方向与加速度的方向不在同一条直线上,知轨迹是曲线,故选项A错误;
当静水速与河岸垂直时,渡河时间最短,t=
s=150
s,故选项B正确,D错
误;船离开河岸400
m时,离河岸较近的距离为200
m,此时水流速度为2
m/s。根
据平行四边形定则v=
m/s=2
m/s,故选项C正确。
3.光滑半球A放在竖直面光滑的墙角,并用手推着保持静止。现在A与墙壁之间放入光滑球B,放手让A和B由静止开始运动,当A、B运动到图示位置时,二者球心的连线与水平面成θ角,速度大小分别为vA和vB,则以下关系正确的是( )
A.vA=vB
B.vA=vBsinθ
C.vA=vBcosθ
D.vA=vBtanθ
【解析】选D。将A、B两球的速度沿两球心的连线和垂直两球心连线分解,如图,由关联速度的关系可得:vAsinθ=vBcosθ,解得:vA=vBtanθ,故D正确。
4.(2020·上饶高一检测)一艘小艇从河岸A处出发渡河,小艇保持与河岸垂直方向行驶,经过10
min到达正对岸下游120
m的C处,如图所示,如果小艇保持原来的速度逆水斜向上游与河岸成α角方向行驶,则经过12.5
min恰好到达正对岸的B处,求:河的宽度。
【解析】设河宽为d,河水流速为v1,船速大小为v2,船两次运动速度合成如图所示。
依题意有:v2t1=v2sinα·t2
BC的距离为:
=v1t1
速度关系为:
=cosα
联立可得:v1=12
m/min
由上可得:sinα=0.8,故cosα=0.6,
河宽:d=v2t1=
×10
m=200
m。
答案:200
m
