正弦定理和余弦定理及其应用
图片预览


文档简介
正弦定理和余弦定理及其应用
(新课标人教版必修5第一章)
一、知识与方法归纳
1.正弦定理与三角形的面积公式(略)
2.正弦定理的应用
(1)利用正弦定理可以解答以下两类三角形问题(包括相关的社会实际问题中的应用题).
①已知三角形的两角及其任意一条边,求其它的边和角.解题的思路是:首先由三角形的内角和定理求出第三个角,然后利用正弦定理求出另外两条边.
②已知三角形的两边和其中一条边所对的角,求其它的边和角. 解题的思路是:首先由正弦定理求出另一条边所对的角,然后由三角形的内角和定理求出第三个角,最后再由正弦定理求出第三条边的大小.
⑵已知a, b和A, 用正弦定理求B时,由于已知三角形的两边和其中一条边所对的角不能确定唯一的三角形,因此,解答此类型的三角形时常常出现无解、一解、两解三种情况.
①若A为锐角时:
;②若A为直角或钝角时:
具体解的情况可列表如下:
⑶在解决实际问题中的应用.
2余弦定理
(1).余弦定理及其推论(略);(2). 余弦定理与勾股定理的关系(略)
(5).余弦定理的应用
⑴.求解三角形问题:利用余弦定理主要解答如下三种.求解三角形问题
①已知三角形的两边和它们的夹角,求三角形的第三边和其他两个角;
②已知三角形的三边,求三角形的三个角;
③已知三角形的两边及其中一边的对角,求三角形的第三边和其余两个角.
⑵判断三角形的形状:
基本思路是围绕三角形的边角关系进行思考,通常有两种途径:
一是利用正弦定理和余弦定理,化边为角; 二是利用正弦定理和余弦定理,化角为边
⑶解决实际应用问题.
3 . 解斜三角形应用题中的几个概念
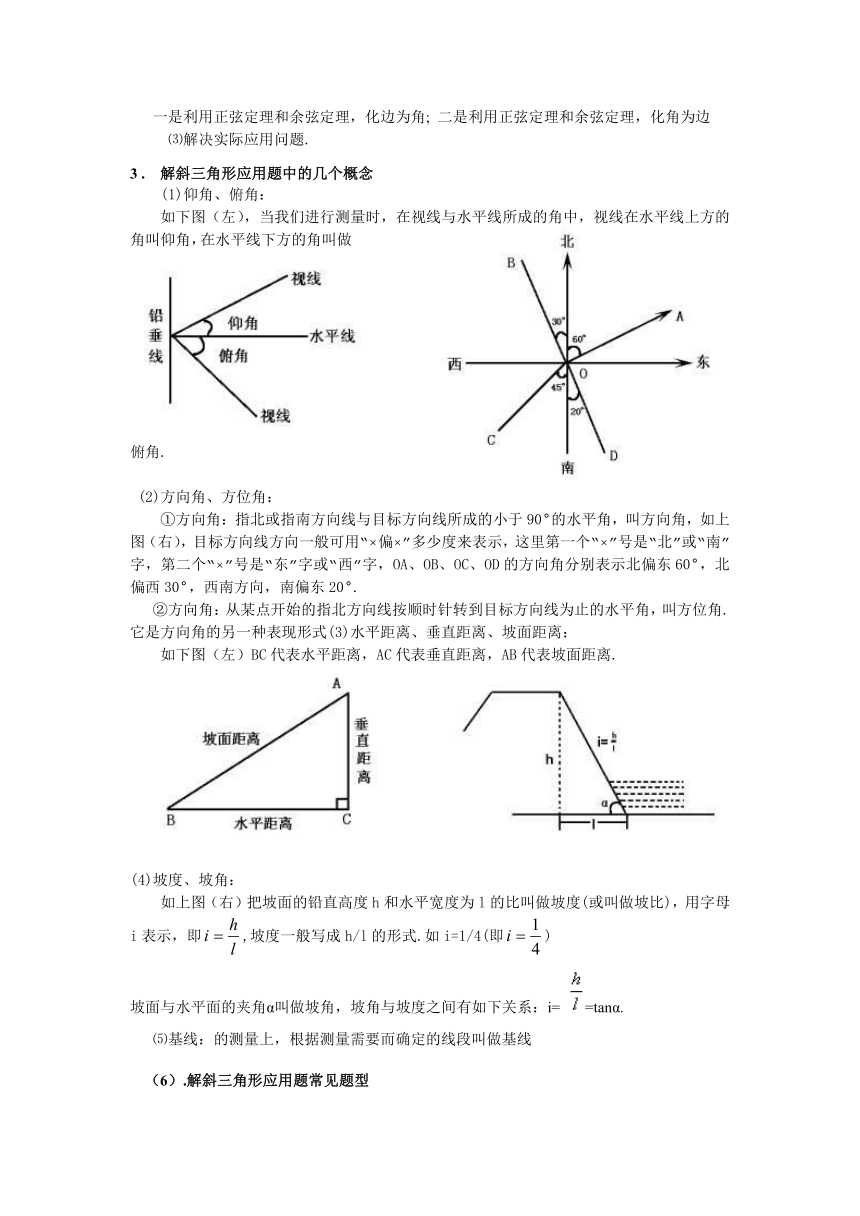
(1)仰角、俯角:
如下图(左),当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫做俯角.
(2)方向角、方位角:
①方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫方向角,如上图(右),目标方向线方向一般可用“×偏×”多少度来表示,这里第一个“×”号是“北”或“南”字,第二个“×”号是“东”字或“西”字,OA、OB、OC、OD的方向角分别表示北偏东60°,北偏西30°,西南方向,南偏东20°.
②方向角:从某点开始的指北方向线按顺时针转到目标方向线为止的水平角,叫方位角.它是方向角的另一种表现形式(3)水平距离、垂直距离、坡面距离:
如下图(左)BC代表水平距离,AC代表垂直距离,AB代表坡面距离.
(4)坡度、坡角:
如上图(右)把坡面的铅直高度h和水平宽度为l的比叫做坡度(或叫做坡比),用字母i表示,即,坡度一般写成h/l的形式.如i=1/4(即)
坡面与水平面的夹角α叫做坡角,坡角与坡度之间有如下关系:i= =tanα.
⑸基线:的测量上,根据测量需要而确定的线段叫做基线
(6).解斜三角形应用题常见题型
主要有以下六种题型即:题型1.测量高度的问题;题型2.测量角度的问题;题型3.测量距离问题包括求水平距离和垂直距离两种,题型4.计算面积问题;题型5.航海问题;题型6.物理学问题.具体分类见下表:
二、典型例题
例1.根据下列条件解三角形:
(1); (2).
例2.根据下列条件,判断有没有解?若有解,判断解的个数.
(1),,,求;(2),,,求;
(3),,,求;(4),,,求;(5),,,求.
例3.(1)在中,已知判断的形状(要求用两种方法).
(2)在中,已知,试判断该三角形的形状(要求用两种方法).
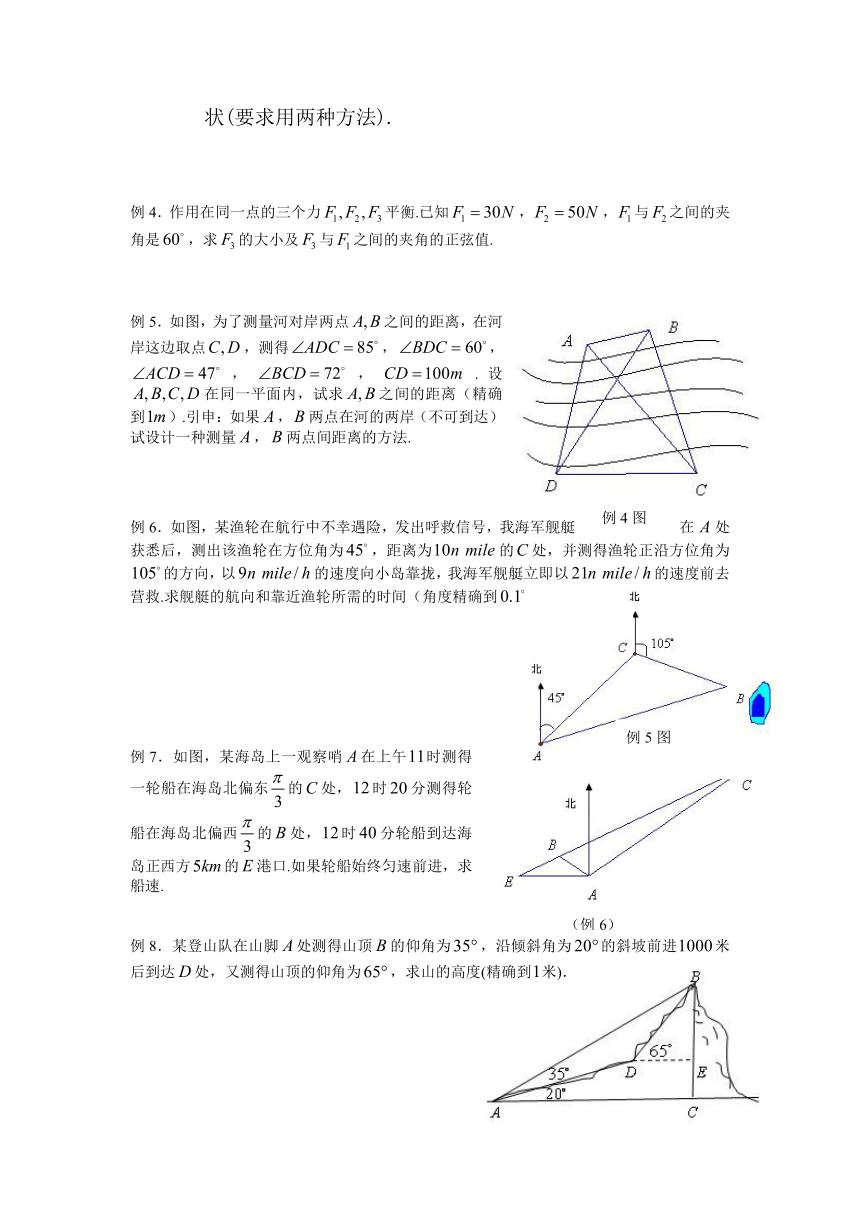
例4.作用在同一点的三个力平衡.已知,,与之间的夹角是,求的大小及与之间的夹角的正弦值.
例5.如图,为了测量河对岸两点之间的距离,在河岸这边取点,测得,,,,.设在同一平面内,试求之间的距离(精确到).引申:如果,两点在河的两岸(不可到达),试设计一种测量,两点间距离的方法.
例6.如图,某渔轮在航行中不幸遇险,发出呼救信号,我海军舰艇在处获悉后,测出该渔轮在方位角为,距离为的处,并测得渔轮正沿方位角为的方向,以的速度向小岛靠拢,我海军舰艇立即以的速度前去营救.求舰艇的航向和靠近渔轮所需的时间(角度精确到,时间精确到).
例7.如图,某海岛上一观察哨在上午时测得一轮船在海岛北偏东的处,时分测得轮船在海岛北偏西的处,时分轮船到达海岛正西方的港口.如果轮船始终匀速前进,求船速.
例8.某登山队在山脚处测得山顶的仰角为,沿倾斜角为的斜坡前进米后到达处,又测得山顶的仰角为,求山的高度(精确到米).
正弦定理和余弦定理及其应用参考答案
例题1解:(1),∴,
,∴,∴为锐角, ∴,∴.
(2),∴,∴,
∴当;
∴当;
所以,.
例题2. 解:(1)∵,∴只能是锐角,因此仅有一解.
(2)∵,∴只能是锐角,因此仅有一解.
(3)由于为锐角,而,即,因此仅有一解.
(4)由于为锐角,而,即,因此有两解,易解得.
(5)由于为锐角,又,即,∴无解.
例题3解:(1)解:令,由正弦定理,得,,.代入已知条件,得,即.又,,,所以,从而为正三角形.
(2)由正弦定理及余弦定理,得,
所以 ,整理得
因为,所以.因此,为等腰三角形.
例4.解:应和合力平衡,所以和在同一直线上,
并且大小相等,方向相反.
如图,在中,由余弦定理,得
.
再由正弦定理,得,
.
答 为,与之间夹角的正弦值是.
例题5解:在中,,,则.又,由正弦定理,得
.
在中,,,
则.又,由正弦定理,得
.
在中,由余弦定理,得
,
所以
答两点之间的距离约为.
本例中看成或的一边,为此需求出,或,,所以可考察和,根据已知条件和正弦定理来求,,再由余弦定理求.
例6.解:设舰艇收到信号后在处靠拢渔轮,则,,又,.
由余弦定理,得
,
即
.
化简,得
,
解得(负值舍去).
由正弦定理,得
,
所以,方位角为.
答 舰艇应沿着方向角的方向航行,经过就可靠近渔轮.
本例是正弦定理、余弦定理在航海问题中的综合应用.因为舰艇从到与渔轮从到的时间相同,所以根据余弦定理可求出该时间,从而求出和;再根据正弦定理求出.
例7.解:设,船的速度为,则,.
在中,,.
在中,,
.
在中,,
,,
船的速度.
例8分析:要求,只要求,为此考虑解.
解:过点作交于,因为,
所以,于是.
又,所以.
在中,由正弦定理,得
.
在中,.
答:山的高度约为.
强化练习(说明:答案在第四页,请同学务必解答后再看).
1.在中,,,是方程的两个根,且,求:①角的度数; ②的长度; ③.
2.(山东07理科)如图,甲船以每小时海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于处时,乙船位于甲船的北偏西的方向处,此时两船相距20海里.当甲船航行20分钟到达处时,乙船航行到甲船的北偏西方向的处,此时两船相距海里,问乙船每小时航行多少海里
1.解:① ∴;
②由题设: ,
∴
, 即;
③.
2. 解:如图,连结,,,
是等边三角形,,
在中,由余弦定理得
,
因此乙船的速度的大小为
答:乙船每小时航行海里.
例4图
例5图
(例6)
例8图
北
乙
甲
(新课标人教版必修5第一章)
一、知识与方法归纳
1.正弦定理与三角形的面积公式(略)
2.正弦定理的应用
(1)利用正弦定理可以解答以下两类三角形问题(包括相关的社会实际问题中的应用题).
①已知三角形的两角及其任意一条边,求其它的边和角.解题的思路是:首先由三角形的内角和定理求出第三个角,然后利用正弦定理求出另外两条边.
②已知三角形的两边和其中一条边所对的角,求其它的边和角. 解题的思路是:首先由正弦定理求出另一条边所对的角,然后由三角形的内角和定理求出第三个角,最后再由正弦定理求出第三条边的大小.
⑵已知a, b和A, 用正弦定理求B时,由于已知三角形的两边和其中一条边所对的角不能确定唯一的三角形,因此,解答此类型的三角形时常常出现无解、一解、两解三种情况.
①若A为锐角时:
;②若A为直角或钝角时:
具体解的情况可列表如下:
⑶在解决实际问题中的应用.
2余弦定理
(1).余弦定理及其推论(略);(2). 余弦定理与勾股定理的关系(略)
(5).余弦定理的应用
⑴.求解三角形问题:利用余弦定理主要解答如下三种.求解三角形问题
①已知三角形的两边和它们的夹角,求三角形的第三边和其他两个角;
②已知三角形的三边,求三角形的三个角;
③已知三角形的两边及其中一边的对角,求三角形的第三边和其余两个角.
⑵判断三角形的形状:
基本思路是围绕三角形的边角关系进行思考,通常有两种途径:
一是利用正弦定理和余弦定理,化边为角; 二是利用正弦定理和余弦定理,化角为边
⑶解决实际应用问题.
3 . 解斜三角形应用题中的几个概念
(1)仰角、俯角:
如下图(左),当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫做俯角.
(2)方向角、方位角:
①方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫方向角,如上图(右),目标方向线方向一般可用“×偏×”多少度来表示,这里第一个“×”号是“北”或“南”字,第二个“×”号是“东”字或“西”字,OA、OB、OC、OD的方向角分别表示北偏东60°,北偏西30°,西南方向,南偏东20°.
②方向角:从某点开始的指北方向线按顺时针转到目标方向线为止的水平角,叫方位角.它是方向角的另一种表现形式(3)水平距离、垂直距离、坡面距离:
如下图(左)BC代表水平距离,AC代表垂直距离,AB代表坡面距离.
(4)坡度、坡角:
如上图(右)把坡面的铅直高度h和水平宽度为l的比叫做坡度(或叫做坡比),用字母i表示,即,坡度一般写成h/l的形式.如i=1/4(即)
坡面与水平面的夹角α叫做坡角,坡角与坡度之间有如下关系:i= =tanα.
⑸基线:的测量上,根据测量需要而确定的线段叫做基线
(6).解斜三角形应用题常见题型
主要有以下六种题型即:题型1.测量高度的问题;题型2.测量角度的问题;题型3.测量距离问题包括求水平距离和垂直距离两种,题型4.计算面积问题;题型5.航海问题;题型6.物理学问题.具体分类见下表:
二、典型例题
例1.根据下列条件解三角形:
(1); (2).
例2.根据下列条件,判断有没有解?若有解,判断解的个数.
(1),,,求;(2),,,求;
(3),,,求;(4),,,求;(5),,,求.
例3.(1)在中,已知判断的形状(要求用两种方法).
(2)在中,已知,试判断该三角形的形状(要求用两种方法).
例4.作用在同一点的三个力平衡.已知,,与之间的夹角是,求的大小及与之间的夹角的正弦值.
例5.如图,为了测量河对岸两点之间的距离,在河岸这边取点,测得,,,,.设在同一平面内,试求之间的距离(精确到).引申:如果,两点在河的两岸(不可到达),试设计一种测量,两点间距离的方法.
例6.如图,某渔轮在航行中不幸遇险,发出呼救信号,我海军舰艇在处获悉后,测出该渔轮在方位角为,距离为的处,并测得渔轮正沿方位角为的方向,以的速度向小岛靠拢,我海军舰艇立即以的速度前去营救.求舰艇的航向和靠近渔轮所需的时间(角度精确到,时间精确到).
例7.如图,某海岛上一观察哨在上午时测得一轮船在海岛北偏东的处,时分测得轮船在海岛北偏西的处,时分轮船到达海岛正西方的港口.如果轮船始终匀速前进,求船速.
例8.某登山队在山脚处测得山顶的仰角为,沿倾斜角为的斜坡前进米后到达处,又测得山顶的仰角为,求山的高度(精确到米).
正弦定理和余弦定理及其应用参考答案
例题1解:(1),∴,
,∴,∴为锐角, ∴,∴.
(2),∴,∴,
∴当;
∴当;
所以,.
例题2. 解:(1)∵,∴只能是锐角,因此仅有一解.
(2)∵,∴只能是锐角,因此仅有一解.
(3)由于为锐角,而,即,因此仅有一解.
(4)由于为锐角,而,即,因此有两解,易解得.
(5)由于为锐角,又,即,∴无解.
例题3解:(1)解:令,由正弦定理,得,,.代入已知条件,得,即.又,,,所以,从而为正三角形.
(2)由正弦定理及余弦定理,得,
所以 ,整理得
因为,所以.因此,为等腰三角形.
例4.解:应和合力平衡,所以和在同一直线上,
并且大小相等,方向相反.
如图,在中,由余弦定理,得
.
再由正弦定理,得,
.
答 为,与之间夹角的正弦值是.
例题5解:在中,,,则.又,由正弦定理,得
.
在中,,,
则.又,由正弦定理,得
.
在中,由余弦定理,得
,
所以
答两点之间的距离约为.
本例中看成或的一边,为此需求出,或,,所以可考察和,根据已知条件和正弦定理来求,,再由余弦定理求.
例6.解:设舰艇收到信号后在处靠拢渔轮,则,,又,.
由余弦定理,得
,
即
.
化简,得
,
解得(负值舍去).
由正弦定理,得
,
所以,方位角为.
答 舰艇应沿着方向角的方向航行,经过就可靠近渔轮.
本例是正弦定理、余弦定理在航海问题中的综合应用.因为舰艇从到与渔轮从到的时间相同,所以根据余弦定理可求出该时间,从而求出和;再根据正弦定理求出.
例7.解:设,船的速度为,则,.
在中,,.
在中,,
.
在中,,
,,
船的速度.
例8分析:要求,只要求,为此考虑解.
解:过点作交于,因为,
所以,于是.
又,所以.
在中,由正弦定理,得
.
在中,.
答:山的高度约为.
强化练习(说明:答案在第四页,请同学务必解答后再看).
1.在中,,,是方程的两个根,且,求:①角的度数; ②的长度; ③.
2.(山东07理科)如图,甲船以每小时海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于处时,乙船位于甲船的北偏西的方向处,此时两船相距20海里.当甲船航行20分钟到达处时,乙船航行到甲船的北偏西方向的处,此时两船相距海里,问乙船每小时航行多少海里
1.解:① ∴;
②由题设: ,
∴
, 即;
③.
2. 解:如图,连结,,,
是等边三角形,,
在中,由余弦定理得
,
因此乙船的速度的大小为
答:乙船每小时航行海里.
例4图
例5图
(例6)
例8图
北
乙
甲
