3.2.1角与角的大小比较课件

(共25张PPT)
复习：
（1）比较线段的大小有哪些方法？
度量法,叠合法
（2）线段有什么性质？
两点之间线段最短
（3）
CB
AB
CB
引言：

小明家新买了一台电冰箱，包装箱上标明：将冰箱向后倾斜
可推动冰箱，但倾斜角不
能超过30度。
什么叫角？什么叫角的度数呢？
这节课我们来学习----
3.2.1角与角的大小比较
主题讲解







主题一 .角的概念
观察：
（1）钟表盘上的时针和
分针， 它们所成的图形
给我们以角的形象．

（2）圆规， 我们可以看到,圆规未打开时可以看做以固定螺丝为端点的一条射线， 当圆规的一支绕固定螺丝旋转开时， 就出现了角的形象．
（3）推开房门时， 门的底边与门框底边也出现了角的形象．
什么叫角呢？






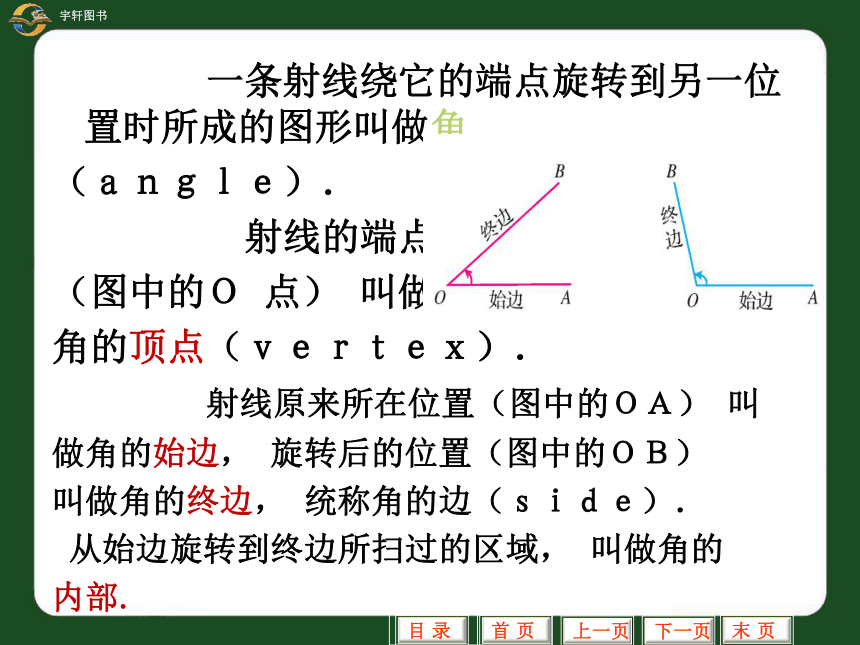
一条射线绕它的端点旋转到另一位置时所成的图形叫做角
（ａｎｇｌｅ）．
射线的端点
（图中的Ｏ 点） 叫做
角的顶点（ｖｅｒｔｅｘ）．
射线原来所在位置（图中的ＯＡ） 叫
做角的始边， 旋转后的位置（图中的ＯＢ）
叫做角的终边， 统称角的边（ｓｉｄｅ）．
从始边旋转到终边所扫过的区域， 叫做角的
内部.
注意！
角的始边可以绕顶点向两个方向
（顺时针方向和逆时针方向） 旋转，
如果没有特别说明， 本书只讲旋转的
量， 不计方向．
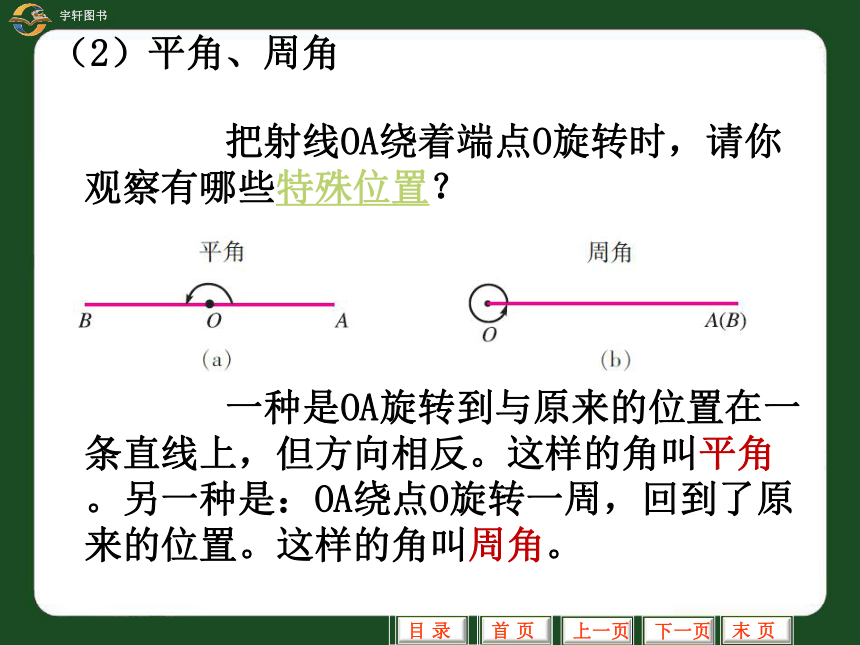
（2）平角、周角

把射线OA绕着端点O旋转时，请你观察有哪些特殊位置？



一种是OA旋转到与原来的位置在一条直线上，但方向相反。这样的角叫平角。另一种是：OA绕点O旋转一周，回到了原来的位置。这样的角叫周角。
（3）角的表示：





方法1 ：用三个大写字母，顶点字母写中间，另外两个字母在角的两边上任意取；如图(1)，角记作：∠AOB.
（图1)
A
B
O
方法2 :角的顶点处画一条弧线，并用数字或希腊字母表示；图（2）中的∠AMN记作∠1，∠MND记作∠2,图（3）中的两个角分别记作∠α、∠β。
方法3 :如果一个角的顶点处只有一个角也可以只用表示顶点的字母表示这个角。
如图（1）中∠AOB可以记作∠ α.
注意！角的大小是由始边旋转的量来确定的。

图3
图2
图1
主题二、比较角的大小


（1）度量法：量出角的度数，就可以根据度数比较两个角的大小了。
使用量角器时，要注意中心对正，一边对齐。
（2）叠合法。
把两个角的顶点对正，一条边对齐，观察另一条边的位置，就可以知道两个角大小。
主题三 、角平分线的概念


做一做
画∠AOB，把∠AOB沿着过点O的一条射线对折，使OA与OB重合。折痕把∠AOB分成的两个角有什么关系？
以一个角的顶点为端点的一条射线，如果把这个角分成两个相等的角，这条射线叫做这个角的平分 线。
思考：1、如图，OC是∠AOB的平分线，那么你能得到什么结论？
因为,OC是∠AOB的平分线，
所以，∠AOC=BOC=0.5∠AOB,
或∠AOB=2∠AOC=2∠BOC
2、如上图，要使OC是∠AOB的平分线需要什么条件？
若∠AOC=BOC,则O就是∠AOB的平分线
应用迁移


【例1】下列说法：（1）有公共端点的两条射线叫做角；（2）两条射线组成的图形叫做角；
（3）有公共端点的两条射线组成的图形叫做角；
（4）一条直线成平角。其中错误的有（ ）
A 1个， B 2个 C 3个 D 4个。
【分析与解】A、角并不是两条射线，所以A不对，B、如图，是两条射线，但不是角，所以B不对，
C、正确，D、角有顶点，直
线没有顶点，所以直线不能
成平角。选C

【变式练习】




1、如图∠AOC可表示为_____,∠1可表示为______.
2、（1）图中能用顶点的大写字母表示的角是有________;
(2)以∠A为顶点的角有_________________________
图2
∠ α
∠ DOB
∠ B
∠ C
∠ BAD,
∠ BAE,
∠ BAC,
∠ DAE,
∠ DAC,
∠ EAC
2、角的大小比较
【例2】如图，若∠AOB=∠COD,那么∠AOC与∠BOD的大小关系是（ ）
A ∠AOC=∠BOD, B ∠AOC﹤∠BOD ，
C ∠AOC>∠BOD, D 不确定

【解】因为∠AOB=∠COD，
所以∠AOB+∠BOC
=∠COD+∠BOC,
即：∠AOC=∠BOD，选A.
【变式练习】
如图，若∠AOB=∠COD,那么∠AOC与∠BOD相等吗？
答：相等，
因为∠AOB=∠COD，
所以∠AOB-∠BOC=∠COD-∠BOC
即：∠AOC=∠BOD
3、角平分线的定义
【例3】如图，OC是∠AOB的平分线，OE是∠BOD的平分线，那么∠COE=_____∠AOD.
【解】因为OC是∠AOB的平分线，
OE是∠BOD的平分线
所以，∠BOC=0.5∠AOB, ∠BOE=0.5∠BOD,
所以，∠BOC+∠BOE=0.5∠AOB+0.5∠BOD
=0.5(∠AOB+∠BOD)
=0.5∠AOD.
【变式练习】
如图，OE是∠COA的平分线，∠AOE=β, ∠AOB=∠COD=α,
(1)用α、β的代数式表示∠BOC=________；
（2）∠AOC_____∠BOD(用“<,>=”填空)。

【解】(1)因为OE平分∠COA,所以 ∠AOE=∠COE=β
因为∠AOB= ∠COD= α
所以， ∠BOE= ∠AOE= ∠AOB= β- α
所以， ∠BOC= ∠BOE+ ∠EOC= β+ β- α
=2 β- α
(2) ∠ AOC=2∠AOE= 2β，
∠BOD= ∠ BOE+∠COE+ ∠COD= β- α+ β+ α=2 β
所以， ∠AOC=∠BOD
【分析】由于∠BOC= ∠BOE+ ∠EOC,由于∠ EOC=∠AOE= β
所以关键是用α、 β表示∠BOE.
课堂练习

１．把图中的每个角用三个字母表示出来．
【解】∠ABC, ∠BCE,∠BCD,∠ECD
２． 对于图中所出现的各个角， 用“ ＞ ” 、“＜”、“＝” 填空：
∠ＡＯＢ____ ∠ＡＯＣ，
∠ＢＯＣ ____∠ＤＯＢ，
∠ＡＯＤ______ ∠ＢＯＣ，
∠ＡＯＤ _____∠ＤＯＡ．







<
<
>
=
３．如 图是一个公园的平面示意图， 请以大门处为端点， 作通过各景点的射线， 然后用字母表示这些射线所形成的几个角．

O
C
B
A
∠AOB
∠AOC
∠BOC
反思小结
这节课你有什么收获？
1、角的大小是由始边旋转的量来确定的。
2、表示角时，如果一个顶点处有几个角，一般用三个大写字母表示，或在角的顶点处画弧线，用数字或希腊字母表示，一个图形中用数字和希腊字母表示角的数量不能太多，否则图形显得混乱。
3、理解角平分线的概念要结合图形，能用式子表示角平分线的含义。
作业：P50 A组1、 2题