8.4空间点、直线、平面之间的位置关系 基础练习-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析)
文档属性
| 名称 | 8.4空间点、直线、平面之间的位置关系 基础练习-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析) | 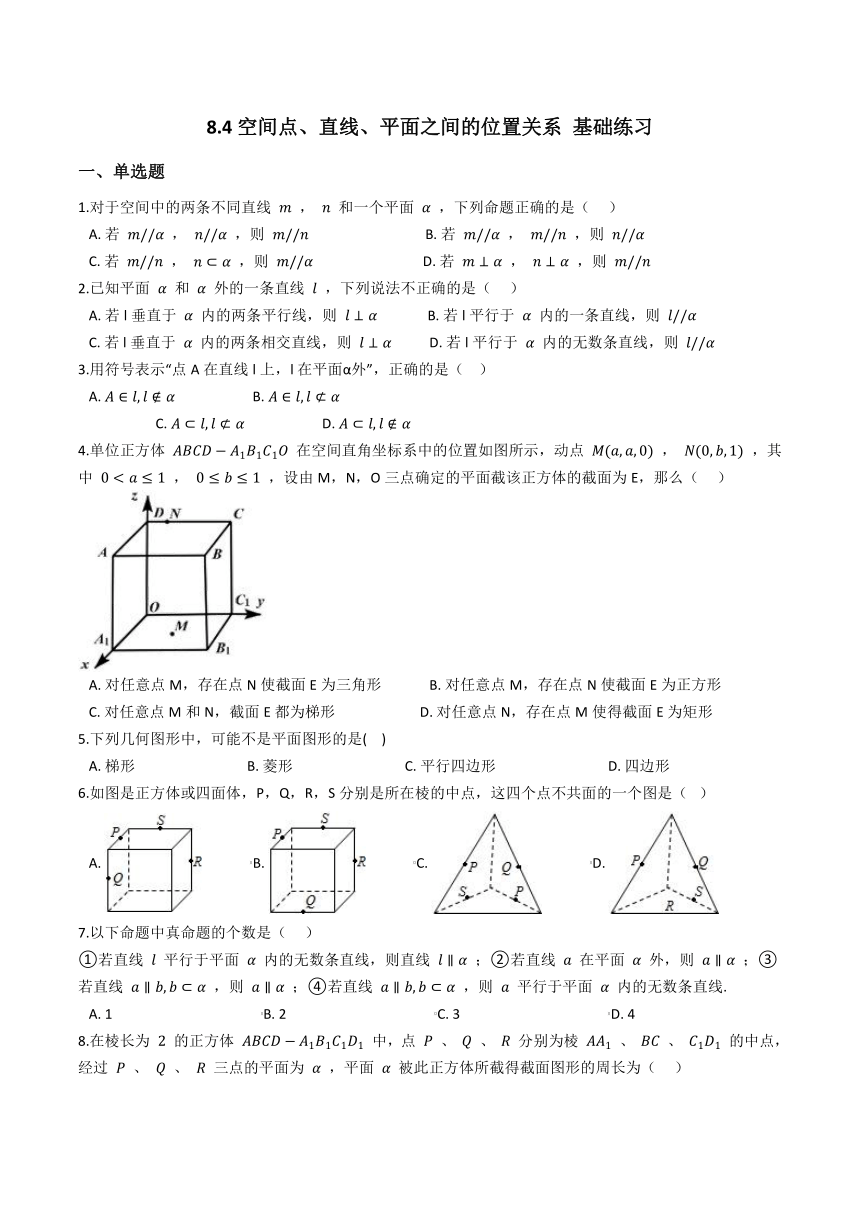 | |
| 格式 | docx | ||
| 文件大小 | 209.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-04 17:39:32 | ||
图片预览




文档简介
8.4空间点、直线、平面之间的位置关系 基础练习
一、单选题
1.对于空间中的两条不同直线 m , n 和一个平面 α ,下列命题正确的是(??? )
A.?若 m//α , n//α ,则 m//n??????????????????????????????????B.?若 m//α , m//n ,则 n//α
C.?若 m//n , n?α ,则 m//α????????????????????????????????D.?若 m⊥α , n⊥α ,则 m//n
2.已知平面 α 和 α 外的一条直线 l ,下列说法不正确的是(??? )
A.?若l垂直于 α 内的两条平行线,则 l⊥α??????????????B.?若l平行于 α 内的一条直线,则 l//α
C.?若l垂直于 α 内的两条相交直线,则 l⊥α???????????D.?若l平行于 α 内的无数条直线,则 l//α
3.用符号表示“点A在直线l上,l在平面α外”,正确的是( ??)
A.?A∈l,l?α??????????????????????B.?A∈l,l?α
??????????????????????C.?A?l,l?α??????????????????????D.?A?l,l?α
4.单位正方体 ABCD?A1B1C1O 在空间直角坐标系中的位置如图所示,动点 M(a,a,0) , N(0,b,1) ,其中 0A.?对任意点M,存在点N使截面E为三角形??????????????B.?对任意点M,存在点N使截面E为正方形
C.?对任意点M和N,截面E都为梯形????????????????????????D.?对任意点N,存在点M使得截面E为矩形
5.下列几何图形中,可能不是平面图形的是( ??)
A.?梯形????????????????????????????????B.?菱形????????????????????????????????C.?平行四边形????????????????????????????????D.?四边形
6.如图是正方体或四面体,P,Q,R,S分别是所在棱的中点,这四个点不共面的一个图是(? )
A.???????????????B.???????????????C.???????????????D.?
7.以下命题中真命题的个数是(??? )
①若直线 l 平行于平面 α 内的无数条直线,则直线 l∥α ;②若直线 a 在平面 α 外,则 a∥α ;③若直线 a∥b,b?α ,则 a∥α ;④若直线 a∥b,b?α ,则 a 平行于平面 α 内的无数条直线.
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
8.在棱长为 2 的正方体 ABCD?A1B1C1D1 中,点 P 、 Q 、 R 分别为棱 AA1 、 BC 、 C1D1 的中点,经过 P 、 Q 、 R 三点的平面为 α ,平面 α 被此正方体所截得截面图形的周长为(??? )
A.?2??????????????????????????????????????B.?62??????????????????????????????????????C.?32??????????????????????????????????????D.?33
9.线段 AB 在平面 α 内,则直线 AB 与平面 α 的位置关系是(??? ).
A.?AB?α?????????????????????B.?AB?α?????????????????????C.?线段 AB 的长短而定?????????????????????D.?以上都不对
10.下列命题中错误的是(??? )
A.?如果平面 α⊥ 平面 γ ,平面 β⊥ 平面 γ , α∩β=l ,那么 l⊥γ
B.?如果平面 α⊥ 平面 β ,那么平面 α 内一定存在直线平行于平面 β
C.?如果平面 α 不垂直于平面 β ,那么平面 α 内一定不存在直线垂直于平面 β
D.?如果平面 α⊥ 平面 β ,过 α 内任意一点作交线的垂线,那么此垂线必垂直于 β
11.下列命题中为真命题的是(??? )
①若 a∥b,a⊥α ,则 b⊥α ;????????? ②若 a⊥α,b⊥α ,则 a∥b ;
③若 a⊥α,a⊥b ,则 b//α ;????????? ④若 a∥α,a⊥b ,则 b⊥α .
A.?①②?????????????????????????????????B.?①②③?????????????????????????????????C.?②③④?????????????????????????????????D.?①②④
12.如图,在四棱锥 P?ABCD 中,底面 ABCD 为矩形,侧棱 AP⊥ 平面 ABCD , AB=1 , AP=3 ,点 M 在线段 BC 上,且 AM⊥MD ,则当 ΔPMD 的面积最小时,线段 BC 的长度为(?? )
A.???????????????????????????????????????B.???????????????????????????????????????C.?2??????????????????????????????????????D.?
13.如果,正方体的底面与正四面体的底面在同一平面α上,且AB//CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n=(?? )
A.?8??????????????????????????????????????????B.?9??????????????????????????????????????????C.?10??????????????????????????????????????????D.?11
14.下列命题错误的是(??? )
A.?命题“ , ”的否定是“ , ”;
B.?若 是假命题,则 , 都是假命题
C.?双曲线 的焦距为
D.?设 , 是互不垂直的两条异面直线,则存在平面 ,使得 ,且
15.下面四个条件中,能确定一个平面的条件是(??? ).
A.?空间任意三点?????????????B.?空间两条直线?????????????C.?空间两条平行直线?????????????D.?一条直线和一个点
16.已知a,b为异面直线,且所成的角为70°,过空间一点作直线l,直线l与a,b均异面,且所成的角均为50°,则满足条件的直线共有(???? ) 条
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
17.有以下三种说法,其中正确的是(?? )
①若直线a与平面α相交,则α内不存在与a平行的直线;
②若直线b∥平面α,直线a与直线b垂直,则直线a不可能与α平行;
③直线a,b满足a∥α,a∥b,且b?α,则a平行于经过b的任何平面.
A.?①②??????????????????????????????????????B.?①③??????????????????????????????????????C.?②③??????????????????????????????????????D.?①
18.如图,已知正方体ABCD-A1B1C1D1 , 则直线EF是平面ACD1与( ??)
A.?平面BDB1的交线???????????B.?平面BDC1的交线???????????C.?平面ACB1的交线???????????D.?平面ACC1的交线
19.三条两两平行的直线可以确定平面的个数为 ( ??)
A.?0????????????????????????????????????????B.?1????????????????????????????????????????C.?0或1????????????????????????????????????????D.?1或3
20.空间四点 的位置关系式( ??)
A.?共线?????????????????????????????????B.?共面?????????????????????????????????C.?不共面?????????????????????????????????D.?无法确定
二、解答题
21.???
(1)已知某圆柱的体积为 3π ,侧面积为 6π ,求该圆柱的高与表面积;
(2)如图, l1//l2 , l3 与 l1 、 l2 分别交于A、B两点, l4 与 l1 、 l2 分别交于C、D两点, E∈AD ,证明:A、B、C、D、E五点共面.
22.在正方体 ABCD-A1B1C1D1 中,E、F分别是 AA1 、 AB 的中点,
(1)证明点E、F、C、 D1 共面
(2)证明 D1E 、 DA 、 CF 三线交于一点
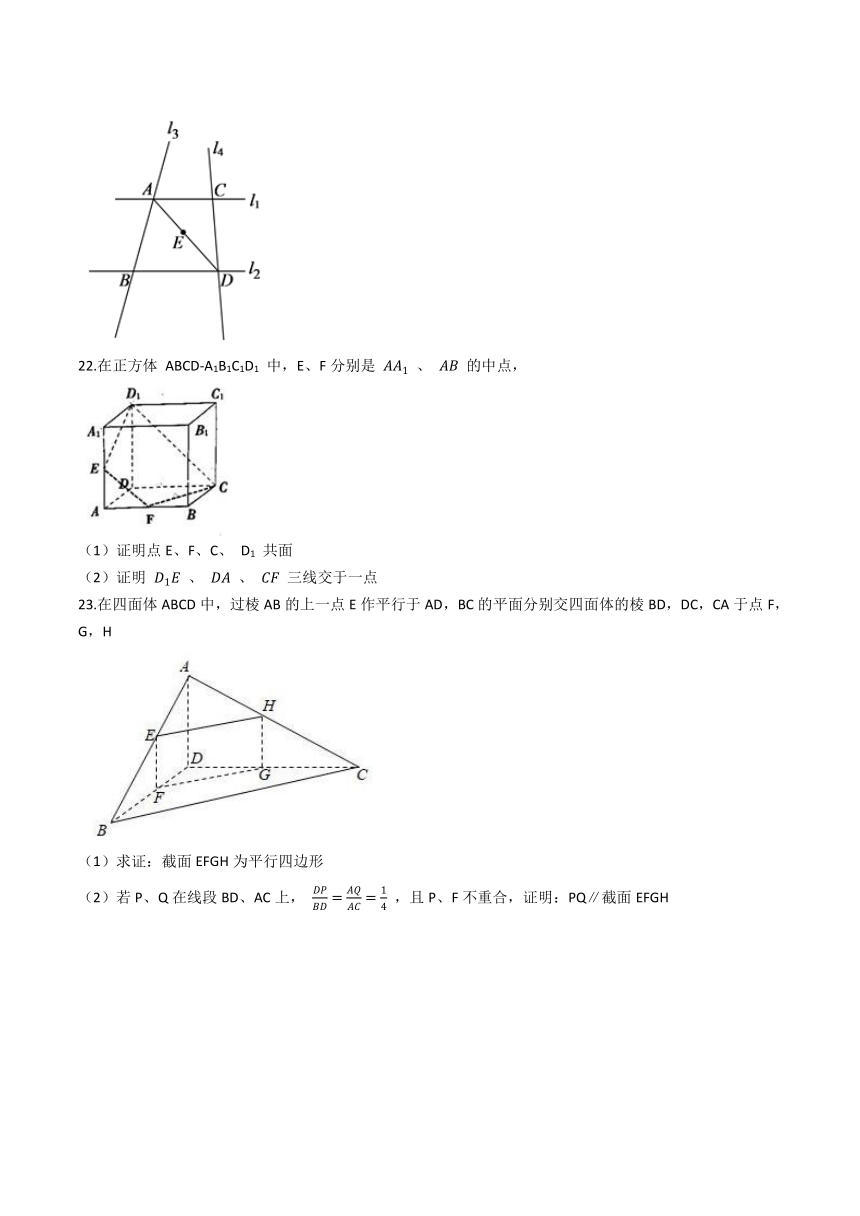
23.在四面体ABCD中,过棱AB的上一点E作平行于AD,BC的平面分别交四面体的棱BD,DC,CA于点F,G,H
(1)求证:截面EFGH为平行四边形
(2)若P、Q在线段BD、AC上, DPBD=AQAC=14 ,且P、F不重合,证明:PQ∥截面EFGH
答案解析部分
一、单选题
1.【答案】 D
【解析】对于A,若 m//α , n//α ,则 m,n 可能平行,相交或者异面,所以不正确;
对于B,若 m//α , m//n ,则 n//α 或者 n?α ,所以不正确;
对于C,若 m//n , n?α ,则 m//α 或者 m?α ,所以不正确;
对于D,垂直于同一平面的两直线平行,所以正确.
故答案为:D
2.【答案】 A
【解析】若l垂直于 α 内的两条相交直线,则 l⊥α ,A错误,符合题意;C正确,不符合题意;
若l平行于 α 内的一条直线,则 l//α ,B正确,不符合题意;
若l平行于 α 内的无数条直线,则 l//α ,D正确,不符合题意.
故答案为:A.
3.【答案】 B
【解析】用“属于”和“不属于”表示点与直线的关系;用“包含”和“不包含”表示直线与平面的关系.故点 Α 在直线 l 上用属于符号 ∈ , l 在平面 α 外用不包含 ? .
故答案为:B.
4.【答案】 A
【解析】由题意可得:动点 M(a,a,0) 且 0即动点M在线段 OB1 (除端点O)上的动点,
N(0,b,1) 且 0≤b≤1 ,
即动点N在线段 DC 上的动点,
所以任意点M,由M,N,O三点确定的平面截该正方体的截面为E都过直线 OB1 ,
当N点与C重合时,截面E为三角形,因此A选项正确;
当点N与D重合时,截面E为矩形,
当点N不与端点C、D重合时,截面E为等腰梯形,
所以 B,C 选项错误;
只有当点N与D重合时,截面E为矩形,所以D选项错误;
故答案为:A
5.【答案】 D
【解析】有定义易知梯形,菱形,平行四边形都是平面图形,
四边形可能是空间四边形,如将菱形沿一条对角线折叠成4个顶点不共面的四边形.
故答案为:D.
6.【答案】 D
【解析】在A图中:分别连接PS,QR,
则PS∥QR,∴P,S,R,Q共面.
在B图中:过P,Q,R,S可作一正六边形,如图,故P,Q,R,S四点共面.
在C图中:分别连接PQ,RS,则PQ∥RS,∴P,Q,R,S共面.
在D图中:PS与RQ为异面直线,∴P,Q,R,S四点不共面.
故答案为:D.
7.【答案】 A
【解析】①③中直线有可能含于 α ;②中直线可能和平面相交; 所以只有④是正确的,
故答案为:A.
8.【答案】 B
【解析】如下图所示,分别取 AB 、 CC1 、 A1D1 的中点 E 、 F 、 G ,连接 AC 、 A1C1 、 PF .
在正方体 ABCD?A1B1C1D1 中, AA1//__CC1 ,又 P 、 F 分别为 AA1 、 CC1 的中点, ∴PA1//__C1F ,
所以,四边形 A1C1FP 为平行四边形,
又 ∵G 、 R 分别为 A1D1 、 C1D1 的中点, ∴GR//A1C1 ,且 GR=12A1C1=2 ,
∴GR=12PF ,则四边形 PFRG 为梯形,则 P 、 F 、 R 、 G 四点共面,
若 E? 平面 PFRG ,易证 PE//RF ,且 PE? 平面 PFRG , RF? 平面 PFRG ,
可得出 PE// 平面 PFRG ,这与 PE∩ 平面 PFRG=P 矛盾,则 E∈ 平面 PFRG ,
同理可证 Q∈ 平面 PFRG ,所以平面 α 截正方体 ABCD?A1B1C1D1 所得截面图形为六边形 EQFRGP ,易知该六边形的边长均为正方体 ABCD?A1B1C1D1 的面对角线长度的一半,则其边长为 2 ,因此,该截面图形的周长为 62 .
故答案为:B.
9.【答案】 A
【解析】∵线段AB在平面α内,
∴.直线AB上所有的点都在平面α内,
∴直线AB与平面a的位置关系:直线在平面a内,用符号表示为: AB?α,
故答案为:A
10.【答案】 D
【解析】A.如果平面 α⊥ 平面 γ ,平面 β⊥ 平面 γ , α∩β=l ,那么 l⊥γ 。正确;
B.如果平面 α⊥ 平面 β ,那么平面 α 内一定存在直线平行于平面 β 。正确;
C.如果平面 α 不垂直于平面 β ,那么平面 α 内一定不存在直线垂直于平面 β 。
正确;
D. 如果平面 α⊥ 平面 β ,过 α 内任意一点作交线的垂线,此垂线不一定垂直于 β ,如图所示,错误.
故答案为:D
11.【答案】 A
【解析】由线面垂直的性质,易知①②正确;
当 a⊥α 且 a⊥b 时,有 b∥α 或 b?α ,③不正确;
当 a∥α,a⊥b 时,有 b 与 a 相交或 b∥α 或 b?α ,④不正确.
故答案为:A
12.【答案】 B
【解析】由题意,设 BM=x , MC=y ,则 BC=AD=x+y .
因为 PA⊥ 平面 ABCD , MD? 平面 ABCD ,
所以 PA⊥MD ,又 AM⊥MD , PAAM=A ,所以 MD⊥ 平面 PAM ,则 PM⊥MD .
易知 AM=x2+1 , MD=y2+1 ,
在 RtΔAMD 中, AM2+MD2=AD2 ,即 x2+1+y2+1=(x+y)2 ,化简得 xy=1 .
在 RtΔPMD 中, PM=x2+4 , MD=y2+1=1x2+1 ,
所以 SΔPMD=12x2+4x2+5≥32 ,
当且仅当 x2=4x2 时,取等号,此时 BC=x+y=322 .
13.【答案】 A
【解析】因为过EF做垂直于CD(AB)的平面 α 垂直平分CD,所以该平面与过AB中点并与AB垂直的平面 β 平行,平面 β 和正方体的4个侧面相交,由于EF和正方体的侧棱不平行,所以它与正方体的六个面所在的平面相交的平面个数为4.同理与CE相交的平面有4个,共8个.
故答案为:A.
14.【答案】 B
【解析】对于A,由于特称命题的否定是特称命题,所以命题“ ?x0∈R , x02+1>3x0 ”的否定是“ ?x∈R , x2+1≤3x ”,是正确的.
对于B, 若 p∧q 是假命题,则 p , q 至少有一个是假命题,所以命题是假命题.
对于C, 双曲线 x22?y23=1 的焦距为2c=2 2+3 ? =25 ,所以是真命题.
对于D, 设 a , b 是互不垂直的两条异面直线,则存在平面 α ,使得 a?α ,且 b∥a ,是真命题.
故答案为:B
15.【答案】 C
【解析】A,空间任意三点,当三点共线时能确定一条直线而不是平面,故不正确;B. 空间两条直线,当两条直线重合时,过这条直线的平面有无数个,故不正确;C. 空间两条平行直线,根据课本中的判定得到是正确的;D. 一条直线和一个点,当这个点在直线上时,过这条直线的平面有无数个,故不正确.
故答案为:C.
16.【答案】 B
【解析】在空间取一点P,经过点P分别作a∥a′,b∥b′,
设直线a′、b′确定平面α,
当直线PM满足它的射影PQ在a′、b′所成角的平分线上时,
PM与a′所成的角等于PM与b′所成的角.
因为直线a,b所成的角为70°,得a′、b′所成锐角等于70°.
所以当PM的射影PQ在a′、b′所成锐角的平分线上时,
PM与a′、b′所成角的范围是[35°,90°).
这种情况下,过点P有两条直线与a′、b′所成的角都是50°.
当PM的射影PQ在a′、b′所成钝角的平分线上时,PM与a′、b′所成角的范围是[55°,90°).
这种情况下,过点P有0条直线(即PM?α时)与a′、b′所成的角都是50°.
综上所述,过空间任意一点P可作与a,b所成的角都是50°的直线有2条.
故答案为:B.
17.【答案】 D
【解析】①正确,若在α内存在一条直线b,使a∥b,则a∥α与“a与平面α相交”矛盾,故①正确;②错误,反例如图(1)所示;③错误,反例如图(2)所示,a,b可能在同一平面内.
故答案为:D
18.【答案】 B
【解析】连接BC1.因为E∈DC1 , F∈BD,所以EF?平面BDC1 , 故EF=平面ACD1∩平面BDC1.
故答案为:B.
19.【答案】 D
【解析】当三条直线是同一平面内的平行直线时,确定一个平面,当三条直线是三棱柱侧棱所在的直线时,确定三个平面.选D.
【分析】分情况讨论,确定确定的平面个数。注意两条平行直线确定一个平面,但第三条直线不一定在该平面内。
20.【答案】 C
【考点】平面的基本性质及推论
【解析】设平面方程为ax+by+cz+d=0,
代入A、B、C、D 四点的坐标,得:
,
解得a=b=c=d=0,
∴A,B,C,D四点不共面.
故答案为:C.
二、解答题
21.【答案】 (1)解:设圆柱的底面半径为 r ,高为 ? ,则 {πr2?=3π2πr?=6π ,解得 {r=1?=3 .
故该圆柱的表面积为 6π+2πr2=8π
(2)解:因为 l1//l2 ,所以 l1 , l2 可以确定一个平面 α .
因为 A∈l1 , D∈l2 ,所以 A∈α , D∈α ,所以 AD?α ,又 E∈AD ,所以 E∈α .
因为 C∈l1 , B∈l2 ,所以 C∈α , B∈α ,
从而A、B、C、D、E五点都在平面 α 内,即A、B、C、D、E五点共面.
【解析】(1)设圆柱的底面半径为r,高为h,根据题意建立关于r、h的方程组,解出这两个量,即可计算出圆柱的表面积;(2)由两平行直线确定一个平面,可得出A、B、C、D共面,然后证明 E 也在这个平面内,即可证明出A、B、C、D、E五点共面.
22.【答案】 (1)解:连接 A1B ,根据正方体的几何性质可知 A1B//CD1 .由于 E,F 分别是 AA1,AB 的中点,所以 EF//A1B ,所以 EF//CD1 ,所以 E,F,C,D1 四点共面.
(2)解:由于 EF//CD1,EF≠CD1 ,所以 D1E 与 CF 延长后必相交,设交点为 P ,由于 P∈D1E? 平面 ADD1A1 , P∈CF? 平面 ABCD ,根据公理3可知, P 在平面 ADD1A1 与平面 ABCD 的交线 DA 上,所以 D1E 、 DA 、 CF 三线交于一点
【解析】(1)通过证明 EF//CD1 ,证得 E,F,C,D1 四点共面.(2)根据公理 3 ,证得 D1E 、 DA 、 CF 三线交于一点.
23.【答案】 (1)证明:∵AD∥平面EFGH,平面ADB 平面EHGH=EF,AD ? 平面ABD,
∴AD∥EF? ∵AD∥平面EHGH,平面ADC 平面EHGH=GH,AD ? 平面ADC,. ∴AD∥GH
由平行公理可得EF∥GH
同理可得EH∥FG
∴四边形EFGH为平行四边形
(2)解:如图在CD上取点M,使 DPBD=DMDC=14 ,连接MQ
则PM∥BC∥FG, AQAC=DMDC=14 ,则QM∥AD∥HG
PM QM=M∴平面PMQ∥平面EHGH
∵PQ ? 平面PMQ
∴PQ∥截面EFGH
【解析】(1)根据题意得出 AD∥EF , AD∥GH 进而得出 EF∥GH ,同理也可得出 EH∥FG ,根据平行四边形的判定即证。
(2)首先 在CD上取点M,使 DPBD=DMDC=14 ,连接MQ ,故有 PM∥BC∥FG ,结合已知条件得出 QM∥AD∥HG ,进而得出 平面PMQ∥平面EHGH ,即证。
一、单选题
1.对于空间中的两条不同直线 m , n 和一个平面 α ,下列命题正确的是(??? )
A.?若 m//α , n//α ,则 m//n??????????????????????????????????B.?若 m//α , m//n ,则 n//α
C.?若 m//n , n?α ,则 m//α????????????????????????????????D.?若 m⊥α , n⊥α ,则 m//n
2.已知平面 α 和 α 外的一条直线 l ,下列说法不正确的是(??? )
A.?若l垂直于 α 内的两条平行线,则 l⊥α??????????????B.?若l平行于 α 内的一条直线,则 l//α
C.?若l垂直于 α 内的两条相交直线,则 l⊥α???????????D.?若l平行于 α 内的无数条直线,则 l//α
3.用符号表示“点A在直线l上,l在平面α外”,正确的是( ??)
A.?A∈l,l?α??????????????????????B.?A∈l,l?α
??????????????????????C.?A?l,l?α??????????????????????D.?A?l,l?α
4.单位正方体 ABCD?A1B1C1O 在空间直角坐标系中的位置如图所示,动点 M(a,a,0) , N(0,b,1) ,其中 0
C.?对任意点M和N,截面E都为梯形????????????????????????D.?对任意点N,存在点M使得截面E为矩形
5.下列几何图形中,可能不是平面图形的是( ??)
A.?梯形????????????????????????????????B.?菱形????????????????????????????????C.?平行四边形????????????????????????????????D.?四边形
6.如图是正方体或四面体,P,Q,R,S分别是所在棱的中点,这四个点不共面的一个图是(? )
A.???????????????B.???????????????C.???????????????D.?
7.以下命题中真命题的个数是(??? )
①若直线 l 平行于平面 α 内的无数条直线,则直线 l∥α ;②若直线 a 在平面 α 外,则 a∥α ;③若直线 a∥b,b?α ,则 a∥α ;④若直线 a∥b,b?α ,则 a 平行于平面 α 内的无数条直线.
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
8.在棱长为 2 的正方体 ABCD?A1B1C1D1 中,点 P 、 Q 、 R 分别为棱 AA1 、 BC 、 C1D1 的中点,经过 P 、 Q 、 R 三点的平面为 α ,平面 α 被此正方体所截得截面图形的周长为(??? )
A.?2??????????????????????????????????????B.?62??????????????????????????????????????C.?32??????????????????????????????????????D.?33
9.线段 AB 在平面 α 内,则直线 AB 与平面 α 的位置关系是(??? ).
A.?AB?α?????????????????????B.?AB?α?????????????????????C.?线段 AB 的长短而定?????????????????????D.?以上都不对
10.下列命题中错误的是(??? )
A.?如果平面 α⊥ 平面 γ ,平面 β⊥ 平面 γ , α∩β=l ,那么 l⊥γ
B.?如果平面 α⊥ 平面 β ,那么平面 α 内一定存在直线平行于平面 β
C.?如果平面 α 不垂直于平面 β ,那么平面 α 内一定不存在直线垂直于平面 β
D.?如果平面 α⊥ 平面 β ,过 α 内任意一点作交线的垂线,那么此垂线必垂直于 β
11.下列命题中为真命题的是(??? )
①若 a∥b,a⊥α ,则 b⊥α ;????????? ②若 a⊥α,b⊥α ,则 a∥b ;
③若 a⊥α,a⊥b ,则 b//α ;????????? ④若 a∥α,a⊥b ,则 b⊥α .
A.?①②?????????????????????????????????B.?①②③?????????????????????????????????C.?②③④?????????????????????????????????D.?①②④
12.如图,在四棱锥 P?ABCD 中,底面 ABCD 为矩形,侧棱 AP⊥ 平面 ABCD , AB=1 , AP=3 ,点 M 在线段 BC 上,且 AM⊥MD ,则当 ΔPMD 的面积最小时,线段 BC 的长度为(?? )
A.???????????????????????????????????????B.???????????????????????????????????????C.?2??????????????????????????????????????D.?
13.如果,正方体的底面与正四面体的底面在同一平面α上,且AB//CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n=(?? )
A.?8??????????????????????????????????????????B.?9??????????????????????????????????????????C.?10??????????????????????????????????????????D.?11
14.下列命题错误的是(??? )
A.?命题“ , ”的否定是“ , ”;
B.?若 是假命题,则 , 都是假命题
C.?双曲线 的焦距为
D.?设 , 是互不垂直的两条异面直线,则存在平面 ,使得 ,且
15.下面四个条件中,能确定一个平面的条件是(??? ).
A.?空间任意三点?????????????B.?空间两条直线?????????????C.?空间两条平行直线?????????????D.?一条直线和一个点
16.已知a,b为异面直线,且所成的角为70°,过空间一点作直线l,直线l与a,b均异面,且所成的角均为50°,则满足条件的直线共有(???? ) 条
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
17.有以下三种说法,其中正确的是(?? )
①若直线a与平面α相交,则α内不存在与a平行的直线;
②若直线b∥平面α,直线a与直线b垂直,则直线a不可能与α平行;
③直线a,b满足a∥α,a∥b,且b?α,则a平行于经过b的任何平面.
A.?①②??????????????????????????????????????B.?①③??????????????????????????????????????C.?②③??????????????????????????????????????D.?①
18.如图,已知正方体ABCD-A1B1C1D1 , 则直线EF是平面ACD1与( ??)
A.?平面BDB1的交线???????????B.?平面BDC1的交线???????????C.?平面ACB1的交线???????????D.?平面ACC1的交线
19.三条两两平行的直线可以确定平面的个数为 ( ??)
A.?0????????????????????????????????????????B.?1????????????????????????????????????????C.?0或1????????????????????????????????????????D.?1或3
20.空间四点 的位置关系式( ??)
A.?共线?????????????????????????????????B.?共面?????????????????????????????????C.?不共面?????????????????????????????????D.?无法确定
二、解答题
21.???
(1)已知某圆柱的体积为 3π ,侧面积为 6π ,求该圆柱的高与表面积;
(2)如图, l1//l2 , l3 与 l1 、 l2 分别交于A、B两点, l4 与 l1 、 l2 分别交于C、D两点, E∈AD ,证明:A、B、C、D、E五点共面.
22.在正方体 ABCD-A1B1C1D1 中,E、F分别是 AA1 、 AB 的中点,
(1)证明点E、F、C、 D1 共面
(2)证明 D1E 、 DA 、 CF 三线交于一点
23.在四面体ABCD中,过棱AB的上一点E作平行于AD,BC的平面分别交四面体的棱BD,DC,CA于点F,G,H
(1)求证:截面EFGH为平行四边形
(2)若P、Q在线段BD、AC上, DPBD=AQAC=14 ,且P、F不重合,证明:PQ∥截面EFGH
答案解析部分
一、单选题
1.【答案】 D
【解析】对于A,若 m//α , n//α ,则 m,n 可能平行,相交或者异面,所以不正确;
对于B,若 m//α , m//n ,则 n//α 或者 n?α ,所以不正确;
对于C,若 m//n , n?α ,则 m//α 或者 m?α ,所以不正确;
对于D,垂直于同一平面的两直线平行,所以正确.
故答案为:D
2.【答案】 A
【解析】若l垂直于 α 内的两条相交直线,则 l⊥α ,A错误,符合题意;C正确,不符合题意;
若l平行于 α 内的一条直线,则 l//α ,B正确,不符合题意;
若l平行于 α 内的无数条直线,则 l//α ,D正确,不符合题意.
故答案为:A.
3.【答案】 B
【解析】用“属于”和“不属于”表示点与直线的关系;用“包含”和“不包含”表示直线与平面的关系.故点 Α 在直线 l 上用属于符号 ∈ , l 在平面 α 外用不包含 ? .
故答案为:B.
4.【答案】 A
【解析】由题意可得:动点 M(a,a,0) 且 0
N(0,b,1) 且 0≤b≤1 ,
即动点N在线段 DC 上的动点,
所以任意点M,由M,N,O三点确定的平面截该正方体的截面为E都过直线 OB1 ,
当N点与C重合时,截面E为三角形,因此A选项正确;
当点N与D重合时,截面E为矩形,
当点N不与端点C、D重合时,截面E为等腰梯形,
所以 B,C 选项错误;
只有当点N与D重合时,截面E为矩形,所以D选项错误;
故答案为:A
5.【答案】 D
【解析】有定义易知梯形,菱形,平行四边形都是平面图形,
四边形可能是空间四边形,如将菱形沿一条对角线折叠成4个顶点不共面的四边形.
故答案为:D.
6.【答案】 D
【解析】在A图中:分别连接PS,QR,
则PS∥QR,∴P,S,R,Q共面.
在B图中:过P,Q,R,S可作一正六边形,如图,故P,Q,R,S四点共面.
在C图中:分别连接PQ,RS,则PQ∥RS,∴P,Q,R,S共面.
在D图中:PS与RQ为异面直线,∴P,Q,R,S四点不共面.
故答案为:D.
7.【答案】 A
【解析】①③中直线有可能含于 α ;②中直线可能和平面相交; 所以只有④是正确的,
故答案为:A.
8.【答案】 B
【解析】如下图所示,分别取 AB 、 CC1 、 A1D1 的中点 E 、 F 、 G ,连接 AC 、 A1C1 、 PF .
在正方体 ABCD?A1B1C1D1 中, AA1//__CC1 ,又 P 、 F 分别为 AA1 、 CC1 的中点, ∴PA1//__C1F ,
所以,四边形 A1C1FP 为平行四边形,
又 ∵G 、 R 分别为 A1D1 、 C1D1 的中点, ∴GR//A1C1 ,且 GR=12A1C1=2 ,
∴GR=12PF ,则四边形 PFRG 为梯形,则 P 、 F 、 R 、 G 四点共面,
若 E? 平面 PFRG ,易证 PE//RF ,且 PE? 平面 PFRG , RF? 平面 PFRG ,
可得出 PE// 平面 PFRG ,这与 PE∩ 平面 PFRG=P 矛盾,则 E∈ 平面 PFRG ,
同理可证 Q∈ 平面 PFRG ,所以平面 α 截正方体 ABCD?A1B1C1D1 所得截面图形为六边形 EQFRGP ,易知该六边形的边长均为正方体 ABCD?A1B1C1D1 的面对角线长度的一半,则其边长为 2 ,因此,该截面图形的周长为 62 .
故答案为:B.
9.【答案】 A
【解析】∵线段AB在平面α内,
∴.直线AB上所有的点都在平面α内,
∴直线AB与平面a的位置关系:直线在平面a内,用符号表示为: AB?α,
故答案为:A
10.【答案】 D
【解析】A.如果平面 α⊥ 平面 γ ,平面 β⊥ 平面 γ , α∩β=l ,那么 l⊥γ 。正确;
B.如果平面 α⊥ 平面 β ,那么平面 α 内一定存在直线平行于平面 β 。正确;
C.如果平面 α 不垂直于平面 β ,那么平面 α 内一定不存在直线垂直于平面 β 。
正确;
D. 如果平面 α⊥ 平面 β ,过 α 内任意一点作交线的垂线,此垂线不一定垂直于 β ,如图所示,错误.
故答案为:D
11.【答案】 A
【解析】由线面垂直的性质,易知①②正确;
当 a⊥α 且 a⊥b 时,有 b∥α 或 b?α ,③不正确;
当 a∥α,a⊥b 时,有 b 与 a 相交或 b∥α 或 b?α ,④不正确.
故答案为:A
12.【答案】 B
【解析】由题意,设 BM=x , MC=y ,则 BC=AD=x+y .
因为 PA⊥ 平面 ABCD , MD? 平面 ABCD ,
所以 PA⊥MD ,又 AM⊥MD , PAAM=A ,所以 MD⊥ 平面 PAM ,则 PM⊥MD .
易知 AM=x2+1 , MD=y2+1 ,
在 RtΔAMD 中, AM2+MD2=AD2 ,即 x2+1+y2+1=(x+y)2 ,化简得 xy=1 .
在 RtΔPMD 中, PM=x2+4 , MD=y2+1=1x2+1 ,
所以 SΔPMD=12x2+4x2+5≥32 ,
当且仅当 x2=4x2 时,取等号,此时 BC=x+y=322 .
13.【答案】 A
【解析】因为过EF做垂直于CD(AB)的平面 α 垂直平分CD,所以该平面与过AB中点并与AB垂直的平面 β 平行,平面 β 和正方体的4个侧面相交,由于EF和正方体的侧棱不平行,所以它与正方体的六个面所在的平面相交的平面个数为4.同理与CE相交的平面有4个,共8个.
故答案为:A.
14.【答案】 B
【解析】对于A,由于特称命题的否定是特称命题,所以命题“ ?x0∈R , x02+1>3x0 ”的否定是“ ?x∈R , x2+1≤3x ”,是正确的.
对于B, 若 p∧q 是假命题,则 p , q 至少有一个是假命题,所以命题是假命题.
对于C, 双曲线 x22?y23=1 的焦距为2c=2 2+3 ? =25 ,所以是真命题.
对于D, 设 a , b 是互不垂直的两条异面直线,则存在平面 α ,使得 a?α ,且 b∥a ,是真命题.
故答案为:B
15.【答案】 C
【解析】A,空间任意三点,当三点共线时能确定一条直线而不是平面,故不正确;B. 空间两条直线,当两条直线重合时,过这条直线的平面有无数个,故不正确;C. 空间两条平行直线,根据课本中的判定得到是正确的;D. 一条直线和一个点,当这个点在直线上时,过这条直线的平面有无数个,故不正确.
故答案为:C.
16.【答案】 B
【解析】在空间取一点P,经过点P分别作a∥a′,b∥b′,
设直线a′、b′确定平面α,
当直线PM满足它的射影PQ在a′、b′所成角的平分线上时,
PM与a′所成的角等于PM与b′所成的角.
因为直线a,b所成的角为70°,得a′、b′所成锐角等于70°.
所以当PM的射影PQ在a′、b′所成锐角的平分线上时,
PM与a′、b′所成角的范围是[35°,90°).
这种情况下,过点P有两条直线与a′、b′所成的角都是50°.
当PM的射影PQ在a′、b′所成钝角的平分线上时,PM与a′、b′所成角的范围是[55°,90°).
这种情况下,过点P有0条直线(即PM?α时)与a′、b′所成的角都是50°.
综上所述,过空间任意一点P可作与a,b所成的角都是50°的直线有2条.
故答案为:B.
17.【答案】 D
【解析】①正确,若在α内存在一条直线b,使a∥b,则a∥α与“a与平面α相交”矛盾,故①正确;②错误,反例如图(1)所示;③错误,反例如图(2)所示,a,b可能在同一平面内.
故答案为:D
18.【答案】 B
【解析】连接BC1.因为E∈DC1 , F∈BD,所以EF?平面BDC1 , 故EF=平面ACD1∩平面BDC1.
故答案为:B.
19.【答案】 D
【解析】当三条直线是同一平面内的平行直线时,确定一个平面,当三条直线是三棱柱侧棱所在的直线时,确定三个平面.选D.
【分析】分情况讨论,确定确定的平面个数。注意两条平行直线确定一个平面,但第三条直线不一定在该平面内。
20.【答案】 C
【考点】平面的基本性质及推论
【解析】设平面方程为ax+by+cz+d=0,
代入A、B、C、D 四点的坐标,得:
,
解得a=b=c=d=0,
∴A,B,C,D四点不共面.
故答案为:C.
二、解答题
21.【答案】 (1)解:设圆柱的底面半径为 r ,高为 ? ,则 {πr2?=3π2πr?=6π ,解得 {r=1?=3 .
故该圆柱的表面积为 6π+2πr2=8π
(2)解:因为 l1//l2 ,所以 l1 , l2 可以确定一个平面 α .
因为 A∈l1 , D∈l2 ,所以 A∈α , D∈α ,所以 AD?α ,又 E∈AD ,所以 E∈α .
因为 C∈l1 , B∈l2 ,所以 C∈α , B∈α ,
从而A、B、C、D、E五点都在平面 α 内,即A、B、C、D、E五点共面.
【解析】(1)设圆柱的底面半径为r,高为h,根据题意建立关于r、h的方程组,解出这两个量,即可计算出圆柱的表面积;(2)由两平行直线确定一个平面,可得出A、B、C、D共面,然后证明 E 也在这个平面内,即可证明出A、B、C、D、E五点共面.
22.【答案】 (1)解:连接 A1B ,根据正方体的几何性质可知 A1B//CD1 .由于 E,F 分别是 AA1,AB 的中点,所以 EF//A1B ,所以 EF//CD1 ,所以 E,F,C,D1 四点共面.
(2)解:由于 EF//CD1,EF≠CD1 ,所以 D1E 与 CF 延长后必相交,设交点为 P ,由于 P∈D1E? 平面 ADD1A1 , P∈CF? 平面 ABCD ,根据公理3可知, P 在平面 ADD1A1 与平面 ABCD 的交线 DA 上,所以 D1E 、 DA 、 CF 三线交于一点
【解析】(1)通过证明 EF//CD1 ,证得 E,F,C,D1 四点共面.(2)根据公理 3 ,证得 D1E 、 DA 、 CF 三线交于一点.
23.【答案】 (1)证明:∵AD∥平面EFGH,平面ADB 平面EHGH=EF,AD ? 平面ABD,
∴AD∥EF? ∵AD∥平面EHGH,平面ADC 平面EHGH=GH,AD ? 平面ADC,. ∴AD∥GH
由平行公理可得EF∥GH
同理可得EH∥FG
∴四边形EFGH为平行四边形
(2)解:如图在CD上取点M,使 DPBD=DMDC=14 ,连接MQ
则PM∥BC∥FG, AQAC=DMDC=14 ,则QM∥AD∥HG
PM QM=M∴平面PMQ∥平面EHGH
∵PQ ? 平面PMQ
∴PQ∥截面EFGH
【解析】(1)根据题意得出 AD∥EF , AD∥GH 进而得出 EF∥GH ,同理也可得出 EH∥FG ,根据平行四边形的判定即证。
(2)首先 在CD上取点M,使 DPBD=DMDC=14 ,连接MQ ,故有 PM∥BC∥FG ,结合已知条件得出 QM∥AD∥HG ,进而得出 平面PMQ∥平面EHGH ,即证。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
