9.1随机抽样 基础练习-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析)
文档属性
| 名称 | 9.1随机抽样 基础练习-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 140.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-04 00:00:00 | ||
图片预览



文档简介
9.1 随机抽样 基础练习
一、单选题
1.现有50件产品编号从1到50,现在从中抽取5件检验,用系统抽样确定所抽取的编号为(?? )
A.?5,10,15,20,25
B.?5,15,20,35,40
C.?5,11,17,23,29
D.?10,20,30,40,50
2.数据12,12,12,14,15的平均数与众数的差为(??? )
A.?2??????????????????????????????????????????B.?1??????????????????????????????????????????C.?-1??????????????????????????????????????????D.?-2
3.某校要调查该校1200名学生的身体健康情况,中男生700名,女生500名,现按性别用分层抽样的方法从中抽取120名学生的体检报告,下列说法错误的是(?? )
A.?总体容量是1200?????????????B.?样本容量是120
?????????????C.?男生应抽取70名?????????????D.?女生应抽取40名
4.一位高三学生在半年时间里经历了七次大考,他把这七次考试的历史成绩统计为如图所示的茎叶图,则该学生成绩的平均数和中位数分别为(??? )
7983454793
A.?84,83???????????????????????????????B.?84,84???????????????????????????????C.?85,84???????????????????????????????D.?85,85
5.某科技研究所对一批新研发的产品长度进行检测(单位:mm),下图是检测结果的频率分布直方图,据此估计这批产品的中位数为(?? )
A.?20??????????????????????????????????????B.?22.5??????????????????????????????????????C.?22.75??????????????????????????????????????D.?25
6.为了加强全民爱眼意识,提高民族健康素质,1996年,卫生部,教育部,团中央等12个部委联合发出通知,将爱眼日活动列为国家节日之一,并确定每年的6月6日为“全国爱眼日”.某校高二(1)班有40名学生,学号为01到40,现采用随机数表法从该班抽取5名学生参加“全国爱眼日”宣传活动.已知随机数表中第6行至第7行的各数如下:
16 22 77 94 39?? 49 54 43 54 82?? 17 37 93 23 78?? 87 35 20 96 43? 84 26 34 91 64
84 42 17 53 31?? 57 24 55 06 88?? 77 04 74 47 67?? 21 76 33 50 25? 83 92 12 06 76
若从随机数表第6行第9列的数开始向右读则抽取的第5名学生的学号是(??? )
A.?17?????????????????????????????????????????B.?23?????????????????????????????????????????C.?35?????????????????????????????????????????D.?37
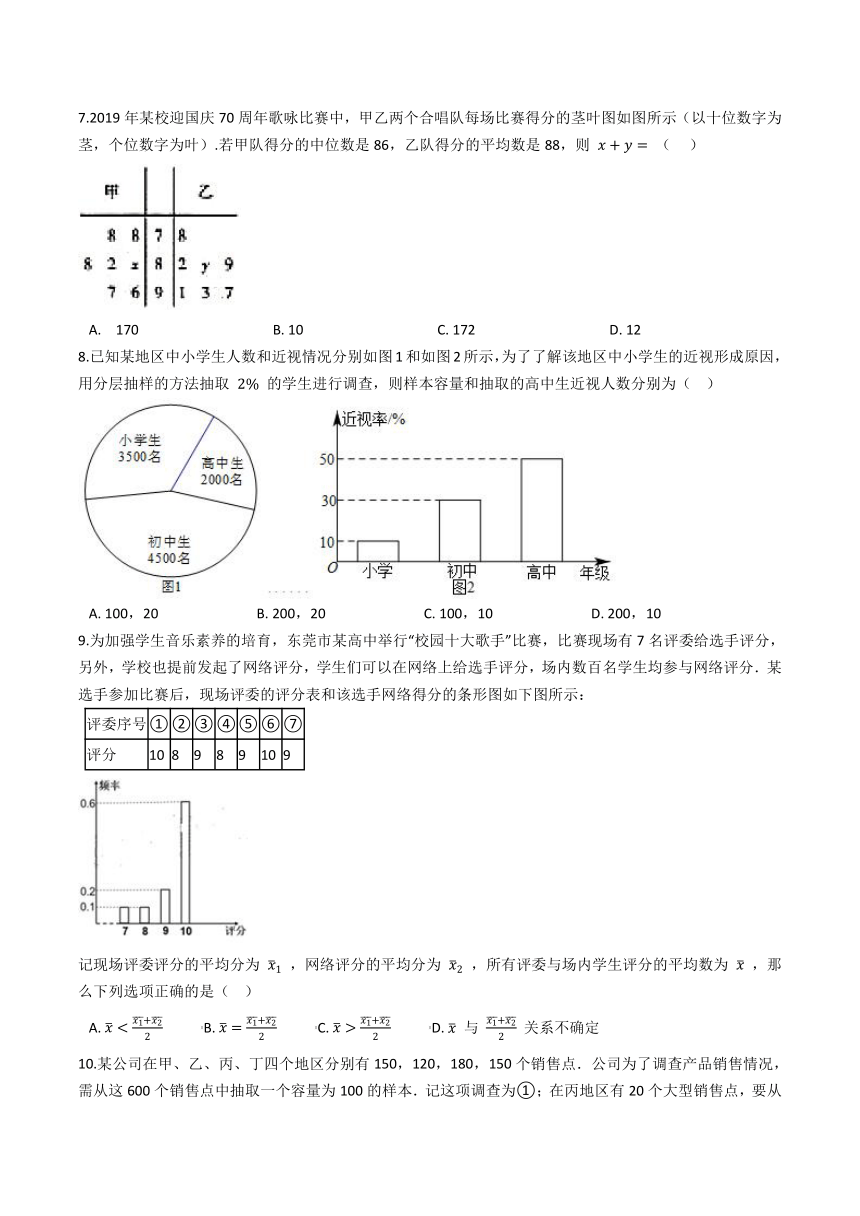
7.2019年某校迎国庆70周年歌咏比赛中,甲乙两个合唱队每场比赛得分的茎叶图如图所示(以十位数字为茎,个位数字为叶).若甲队得分的中位数是86,乙队得分的平均数是88,则 x+y= (??? )
A.?? 170???????????????????????????????????????B.?10???????????????????????????????????????C.?172???????????????????????????????????????D.?12
8.已知某地区中小学生人数和近视情况分别如图1和如图2所示,为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取 2% 的学生进行调查,则样本容量和抽取的高中生近视人数分别为(?? )
A.?100,20????????????????????????????B.?200,20????????????????????????????C.?100,10????????????????????????????D.?200,10
9.为加强学生音乐素养的培育,东莞市某高中举行“校园十大歌手”比赛,比赛现场有7名评委给选手评分,另外,学校也提前发起了网络评分,学生们可以在网络上给选手评分,场内数百名学生均参与网络评分.某选手参加比赛后,现场评委的评分表和该选手网络得分的条形图如下图所示:
评委序号
①
②
③
④
⑤
⑥
⑦
评分
10
8
9
8
9
10
9
记现场评委评分的平均分为 x1 ,网络评分的平均分为 x2 ,所有评委与场内学生评分的平均数为 x ,那么下列选项正确的是(?? )
A.?xx1+x22???????????D.?x 与 x1+x22 关系不确定
10.某公司在甲、乙、丙、丁四个地区分别有150,120,180,150个销售点.公司为了调查产品销售情况,需从这600个销售点中抽取一个容量为100的样本.记这项调查为①;在丙地区有20个大型销售点,要从中抽取7个调查其销售收入和售后服务等情况,记这项调查为②,则完成①,②这两项调查宜采用的抽样方法依次是( )
A.?分层抽样法,系统抽样法????????????????????????????????????B.?分层抽样法,简单随机抽样法
C.?系统抽样法,分层抽样法????????????????????????????????????D.?简单随机抽样法,分层抽样法
11.我国古代数学名著《九章算术》中有如下问题:“今有北乡8100人,西乡有7488人,南乡有6912人,现要按人数多少从三个乡共征集300人,问从各乡征集多少人”.在上述问题中,需从北乡征集的人数大约是(??? )
A.?112??????????????????????????????????????B.?108??????????????????????????????????????C.?130??????????????????????????????????????D.?168
12.已知甲、乙两组数据用茎叶图表示如图所示,若它们的中位数相同, 平均数也相同,则图中的 m,n 的比值 mn 等于( ??)
A.?38??????????????????????????????????????????B.?29??????????????????????????????????????????C.?13??????????????????????????????????????????D.?12
13.为了解某社区居民有无收看“青运会开幕式”,某记者分别从某社区 60?70 岁, 40?50 岁, 20?30 岁的三个年龄段中的 160 人, x 人, 200 人中,采用分层抽样的方法共抽查了 30 人进行调查,若在 60?70 岁这个年龄段中抽查了 8 人,那么 x 为(?? )
A.?120??????????????????????????????????????B.?180??????????????????????????????????????C.?220??????????????????????????????????????D.?240
14.下边茎叶图记录了甲、乙两组各6名学生在一次数学测试中的成绩(单位:分),已知甲组数据的众数为124,乙组数据的平均数为甲组数据的中位数,则 x,y 的值分别为(?? )
A.?4,4????????????????????????????????????B.?5,4????????????????????????????????????C.?4,5????????????????????????????????????D.?5,5
15.某公司在甲、乙、丙、丁四个地区分别有150,120,180,150个销售点.公司为了调查产品销售情况,需从这600个销售点中抽取一个容量为100的样本.按照分层抽样的方法抽取样本,则丙地区抽取的销售点比乙地区抽取的销售点多(?? )
A.?5个?????????????????????????????????????B.?8个?????????????????????????????????????C.?10个?????????????????????????????????????D.?12个
16.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是( ??)
A.?中位数??????????????????????????????????B.?平均数??????????????????????????????????C.?方差??????????????????????????????????D.?极差
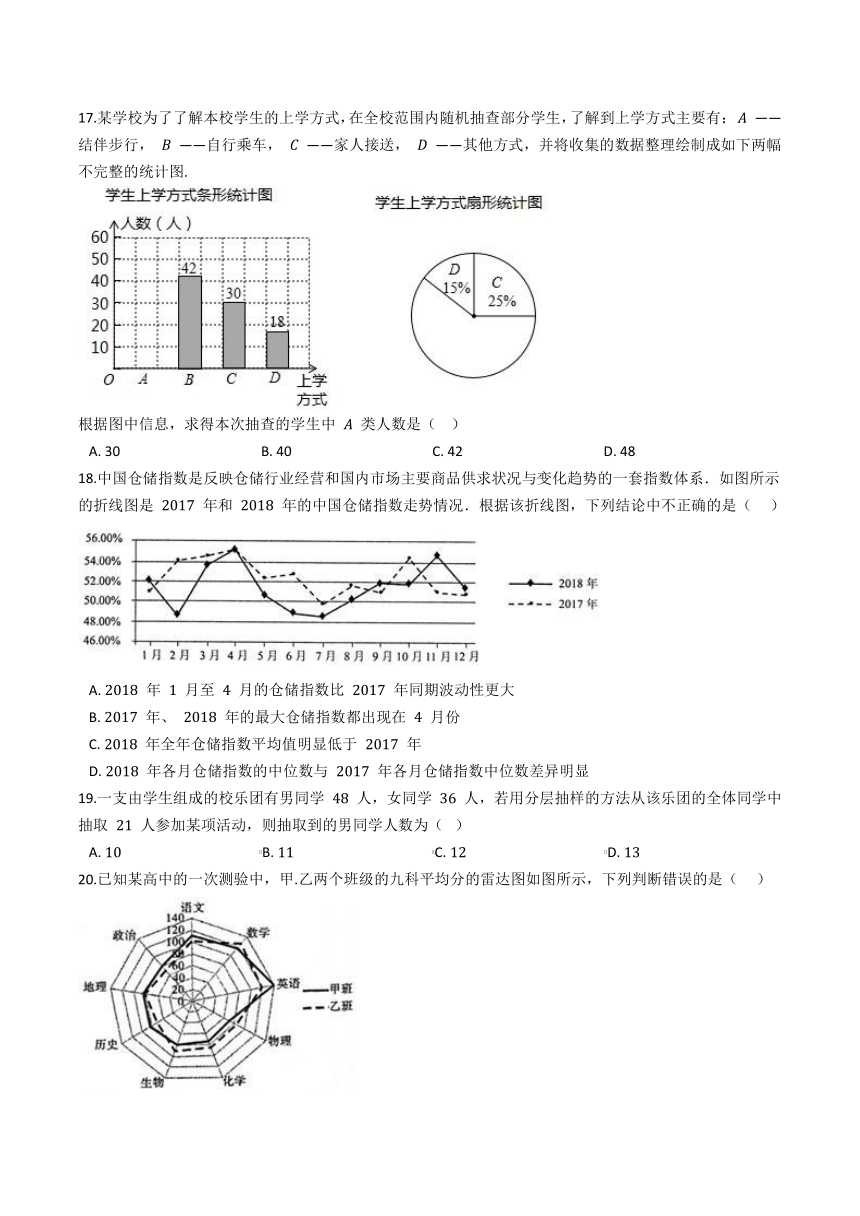
17.某学校为了了解本校学生的上学方式,在全校范围内随机抽查部分学生,了解到上学方式主要有: A ——结伴步行, B ——自行乘车, C ——家人接送, D ——其他方式,并将收集的数据整理绘制成如下两幅不完整的统计图.
根据图中信息,求得本次抽查的学生中 A 类人数是(?? )
A.?30?????????????????????????????????????????B.?40?????????????????????????????????????????C.?42?????????????????????????????????????????D.?48
18.中国仓储指数是反映仓储行业经营和国内市场主要商品供求状况与变化趋势的一套指数体系.如图所示的折线图是 2017 年和 2018 年的中国仓储指数走势情况.根据该折线图,下列结论中不正确的是(??? )
A.?2018 年 1 月至 4 月的仓储指数比 2017 年同期波动性更大
B.?2017 年、 2018 年的最大仓储指数都出现在 4 月份
C.?2018 年全年仓储指数平均值明显低于 2017 年
D.?2018 年各月仓储指数的中位数与 2017 年各月仓储指数中位数差异明显
19.一支由学生组成的校乐团有男同学 48 人,女同学 36 人,若用分层抽样的方法从该乐团的全体同学中抽取 21 人参加某项活动,则抽取到的男同学人数为(? )
A.?10????????????????????????????????????????B.?11????????????????????????????????????????C.?12????????????????????????????????????????D.?13
20.已知某高中的一次测验中,甲.乙两个班级的九科平均分的雷达图如图所示,下列判断错误的是(??? )
A.?乙班的理科综合成绩强于甲班?????????????????????????????B.?甲班的文科综合成绩强于乙班
C.?两班的英语平均分分差最大????????????????????????????????D.?两班的语文平均分分差最小
二、解答题
21.“工资条里显红利,个税新政人民心”,随着2021年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革至2019年实施以来发挥巨大作用.个税新政主要内容包括:
⑴个税起征点为5000元;
⑵每月应纳税所得额(含税) = 收入-个税起征点-专项附加扣除;
⑶专项附加扣除包括住房?子女教育和赡养老人等.新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如表:
旧个税税率表(税起征点3500元)
新个税税率表(个税起征点5000元)
缴税级数
每月应纳税所得额(含税) = 收入-个税起征点
税率(%)
每月应纳税所得额(含税)=收入-个税起征点 ? 专项附加扣除
税率(%)
1
不超过1500元部分
3
不超过3000元部分
3
2
超过1500元至4500元部分
10
超过3000元至12000元部分
10
3
超过4500元至9000元的部分
20
超过12000元至25000元的部分
20
4
超过9000元至35000元的部分
25
超过25000元至35000元的部分
25
5
超过35000元至55000元部分
30
超过35000元至55000元部分
30
?
?
?
?
?
随机抽取某市1000名同一收入层级的IT从业者的相关资料,经统计分析,预估他们2021年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是 2:1:1:1 ;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等.假设该市该收入层级的IT从业者都独自享受专项附加扣除,将预估的该市该收入层级的IT从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:
(1)求该市该收入层级的IT从业者2021年月缴个税的所有可能及其概率.
(2)根据新旧个税方案,估计从2021年1月开始,经过多少个月,该市该收入层级的 IT 从业者各月少缴交的个税之和就超过2019年的月收入?
22.某企业三月中旬生产 A , B , C 三种产品共3000件,根据分层随机抽样的结果,企业统计员制作了如下的统计表格:
产品类别
A
B
C
产品数量
1300
样本中的数量
130
由于不小心,表格中 A , C 产品的有关数据已被污染得看不清楚,统计员只记得样本中 A 产品的数量比样本中 C 产品的数量多10.根据以上信息,求该企业生产 C 产品的数量.
23.? 2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间 X (单位:小时)并绘制如图所示的频率分布直方图.
(1)求这200名学生每周阅读时间的样本平均数 x 和中位数 a ( a 的值精确到0.01);
(2)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为 [6.5,7.5) , [7.5,8.5) 的学生中抽取9名参加座谈会.
(i)你认为9个名额应该怎么分配?并说明理由;
(ii)座谈中发现9名学生中理工类专业的较多.请根据200名学生的调研数据,填写下面的列联表,并判断是否有 95% 的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?
阅读时间不足8.5小时
阅读时间超过8.5小时
理工类专业
40
60
非理工类专业
附: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d) ( n=a+b+c+d ).
临界值表:
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
答案解析部分
一、单选题
1.【答案】 D
【解析】把50件产品分成5组:1—10,11—20,21—30,31—40,41—50,在第一组中用简单随机抽样抽取一个样本,然后在后面的每一组中等距离的抽取样本.
故答案为:D.
2.【答案】 B
【解析】解:平均数为 12+12+12+14+155=13 ,众数为12,差为1.
故答案为:B
3.【答案】 D
【解析】易知A,B符合题意.男生应抽取 7001200×120=70 名,女生应抽取 5001200×120=50 名.C符合题意,D不符合题意.
故答案为:D
4.【答案】 C
【解析】依题意,平均数是 80+17×(?1+3+4×2+5+7+13)=85 ,数据从小到大依次为79,83,84,84,85,87,93,故中位数为84.
故答案为:C
5.【答案】 B
【解析】根据频率分布直方图,得;∵0.02×5+0.04×5=0.3<0.5,0.3+0.08×5=0.7>0.5;
∴中位数应在20~25内,设中位数为x,则0.3+(x-20)×0.08=0.5,解得x=22.5;
∴这批产品的中位数是22.5
故答案为:B
6.【答案】 C
【解析】解:读取的前5名学生的学号依次是:39,17,37,23,35,
故答案为:C.
7.【答案】 D
【解析】由茎叶图知,甲的中位数为 80+x=86 ,故 x=6 ;
乙的平均数为 78+82+80+y+89+91+93+977=88 ,
解得 y=6 ,所以 x+y=12 .
故答案为:D.
8.【答案】 B
【解析】由题意知,样本容量为 (3500+4500+2000)×2%=200 ,其中高中生人数为 2000×2%=40 ,
高中生的近视人数为 40×50%=20 ,
故答案为:B.
9.【答案】 C
【解析】 x1=10+8+9+8+9+10+97=9 , x2=0.1×7+0.1×8+0.2×9+0.6×10=9.3 ,
则 x1+x22=9.15 ,设场内学生人数为 a(a>100) ,
则 x=9.3a+63a+7=9.3(a+7)?2.1a+7=9.3?2.1a+7 ,
因为 a>100 ,
所以 x=9.3?2.1a+7>9.3?2.1107≈9.28>x1+x22 ,
故答案为:C.
10.【答案】 B
【解析】依据题意,第①项调查中,总体中的个体差异较大,应采用分层抽样法;第②项调查总体中个体较少,应采用简单随机抽样法.
故答案为:B.
11.【答案】 B
【解析】由题,则 300×81008100+7488+6912=108 ,
故答案为:B
12.【答案】 A
【解析】甲组数据: 27,30+m,39 ,中位数为 30+m ,
乙组数据: 20+n,32,34,38 ,中位数为: 32+342=33 ,
所以 x甲=27+(30+m)+393=96+m3,x乙=(20+n)+32+34+384=124+n4 ,
所以 {30+m=33,96+m3=124+n4?{m=3,n=8,?mn=38 ,
故答案为:A.
13.【答案】 D
【解析】由题得 30160+x+200=8160 ,
所以x=240.
故答案为:D
14.【答案】 C
【解析】因为甲组数据的众数是124,所以 x=4 .因为乙组数据的平均数等于甲组数据的中位数,即124.所以 124×6?114?118?122?127?138=125 ,所以 y=5 .
故答案为:C.
15.【答案】 C
【解析】由题意
乙地区抽取 120600×100=20 (个)
丙地区抽取 180600×100=30 (个)
30?20=10 (个)
丙地区抽取的销售点比乙地区抽取的销售点多10个;
故答案为: C
16.【答案】 A
【解析】A项,中位数是以通过排序后的最中间一位数,不受最大、最小两个极端数值的影响。故A项正确,符合题意。B项,平均数是指一组数据之和再除以数据的个数,因此不论哪一个数据的变化都有可能影响一组数据的平均数,故B项错误。C项,方差是各个数据与平均数之差的平方的平均数。因此一组数据中的任何一个数据的变化都有可能使方差变化,故C项错误。D项,极差是指最大值减最小值后所得的数值,题中将最大,最小值除去了,故有可能影响数据的极差,故D项错误。
故答案为:A
17.【答案】 A
【解析】解:根据选择D方式的有18人,所占比例为15%,得总人数为 1815%= 120人,故选择A方式的人数为120﹣42﹣30﹣18=30人.
故答案为:A.
18.【答案】 D
【解析】对于A,由图可得 2017 年 1 月至 4 月的仓储指数变化平缓,而 2018 年 1 月至 4 月的仓储指数的波动较大,所以A符合题意.
对于B,由图可得 2017 年、 2018 年的最大仓储指数都出现在 4 月份,所以B符合题意.
对于C,由图可得4月份两年的仓储指数相同,9月、11月、12月的仓储指数2018年比2017年低,其余个月份都是2018年的低,并且有明显的差异,所以 2018 年全年仓储指数平均值明显低于 2017 年,所以C符合题意.
对于D,由图中的数据可得两年的仓储指数的中位数都在51.5左右,差别不大,所以D不正确.
故答案为:D.
19.【答案】 C
【解析】用分层抽样的方法从校乐团中抽取 21 人,所得抽样比为 2148+36=14 ,因此抽取到的男同学人数为 48×14=12 人.
故答案为:C
20.【答案】 D
【解析】由甲、乙两个班级的九科平均分的雷达图可得:
乙班的理科综合成绩强于甲班,即选项 A 正确,
甲班的文科综合成绩强于乙班,即选项 B 正确,
两班的英语平均分分差最大,即选项 C 正确,
两班地理平均分分差最小,即选项 D 错误,
故答案为:D.
二、解答题
21.【答案】 (1)解:由题意,既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是 2:1:1:1 .
①既不符合子女教育扣除又不符合赡养老人扣除的人群每月应纳税所得额为
24000?5000?1000=18000 元,
月缴个税为 3000×0.03+9000×0.1+6000×0.2=2190 元,其概率为 25 ;
②只符合子女教育扣除但不符合赡养老人扣除的人群每月应纳税所得额为
24000?5000?1000?1000=17000 元,
月缴个税为 3000×0.03+9000×0.1+5000×0.2=1990 元,其概率为 15 ;
③只符合赡养老人扣除但不符合子女教育扣除的人群每月应纳税所得额为 24000?5000?1000?2000=16000 元,
月缴个税为 3000×0.03+9000×0.1+4000×0.2=1790 元,其概率为 15 ;
④既符合子女教育扣除又符合赡养老人扣除的人群每月应纳税所得额为 24000?5000?1000?1000?2000=15000 元,
月缴个税为 3000×0.03+9000×0.1+3000×0.2=1590 元,其概率为 15 ;
(2)解:在旧政策下,该收入阶层的 IT 从业者每月应纳税所得额为 24000?3500=20500 元,
故月缴个税为 1500×0.03+3000×0.1+4500×0.2+11500×0.25=4120 元,
在新政策下,该收入阶层的 IT 从业者每月应纳税所得额为 2190×25+(1990+1790+1590)×15=1950 元,
每月少缴个税 4120?1950=2170 元,
设经过 x 个月该市该收入阶层的 IT 从业者各月少缴交的个税之和就超过2019年的月收入,
则 2170x≥24000 ,又 x∈N ,解得 x≥12(x∈N) ,
所以经过12个月,该市该收入阶层的 IT 从业者各月少缴交的个税之和就超过2019年的月收入.
【解析】 (1)根据题中给出的信息,分四种情况按照条件中的计算公式分别求出月缴个税即可;
(2)计算两种政策下的每月应缴个税额度差,然后列出不等式,求解即可得到答案.
22.【答案】 解:设样本量为 x ,
则 x3000×1300=130 ,
∴x=300 ,
∴ 在样本中 A 产品和 C 产品共有 300?130=170 (件).
设样本中 C 产品数量为 y ,则 y+y+10=170 ,
∴y=80 ,
∴ 该企业生产 C 产品的数量为 3000300×80=800 .
【解析】根据题意由分层抽样的定义代入数值计算出结果即可。
?
23.【答案】 (1)解:该组数据的平均数 x=6×0.03+7×0.1+8×0.2+9×0.35+10×0.19 +11×0.09+12×0.04=9 ,
因为 0.03+0.1+0.2+0.35=0.68>0.5 ,所以中位数 a∈[8.5,9.5) ,
由 0.03+0.1+0.2+(a?8.5)×0.35=0.5 ,解得 a=0.5?0.330.35+8.5≈8.99
(2)解:(i)每周阅读时间为 [6.5,7.5) 的学生中抽取3名,每周阅读时间为 [7.5,8.5) 的学生中抽取6名.
理由:每周阅读时间为 [6.5,7.5) 与每周阅读时间为 [7.5,8.5) 是差异明显的两层,为保持样本结构与总体结构的一致性,提高样本的代表性,宜采用分层抽样的方法抽取样本;因为两者频率分别为0.1,0.2,所以按照 1:2 进行名额分配.
(ii)由频率分布直方图可知,阅读时间不足8.5小时的学生共有 200×(0.03+0.1+0.2)=66 人,超过8.5小时的共有 200?66=134 人.
于是列联表为:
阅读时间不足8.5小时
阅读时间超过8.5小时
理工类专业
40
60
非理工类专业
26
74
K2 的观测值 k=200×(40×74?26×60)266×134×100×100≈4.432>3.841 ,
所以有 95% 的把握认为学生阅读时间不足与“是否理工类专业”有关
【解析】(1)根据平均数,中位数的定义进行求解即可(2)完成列联表,计算 K2 的观测值,结合独立性检验的性质进行判断即可.
一、单选题
1.现有50件产品编号从1到50,现在从中抽取5件检验,用系统抽样确定所抽取的编号为(?? )
A.?5,10,15,20,25
B.?5,15,20,35,40
C.?5,11,17,23,29
D.?10,20,30,40,50
2.数据12,12,12,14,15的平均数与众数的差为(??? )
A.?2??????????????????????????????????????????B.?1??????????????????????????????????????????C.?-1??????????????????????????????????????????D.?-2
3.某校要调查该校1200名学生的身体健康情况,中男生700名,女生500名,现按性别用分层抽样的方法从中抽取120名学生的体检报告,下列说法错误的是(?? )
A.?总体容量是1200?????????????B.?样本容量是120
?????????????C.?男生应抽取70名?????????????D.?女生应抽取40名
4.一位高三学生在半年时间里经历了七次大考,他把这七次考试的历史成绩统计为如图所示的茎叶图,则该学生成绩的平均数和中位数分别为(??? )
7983454793
A.?84,83???????????????????????????????B.?84,84???????????????????????????????C.?85,84???????????????????????????????D.?85,85
5.某科技研究所对一批新研发的产品长度进行检测(单位:mm),下图是检测结果的频率分布直方图,据此估计这批产品的中位数为(?? )
A.?20??????????????????????????????????????B.?22.5??????????????????????????????????????C.?22.75??????????????????????????????????????D.?25
6.为了加强全民爱眼意识,提高民族健康素质,1996年,卫生部,教育部,团中央等12个部委联合发出通知,将爱眼日活动列为国家节日之一,并确定每年的6月6日为“全国爱眼日”.某校高二(1)班有40名学生,学号为01到40,现采用随机数表法从该班抽取5名学生参加“全国爱眼日”宣传活动.已知随机数表中第6行至第7行的各数如下:
16 22 77 94 39?? 49 54 43 54 82?? 17 37 93 23 78?? 87 35 20 96 43? 84 26 34 91 64
84 42 17 53 31?? 57 24 55 06 88?? 77 04 74 47 67?? 21 76 33 50 25? 83 92 12 06 76
若从随机数表第6行第9列的数开始向右读则抽取的第5名学生的学号是(??? )
A.?17?????????????????????????????????????????B.?23?????????????????????????????????????????C.?35?????????????????????????????????????????D.?37
7.2019年某校迎国庆70周年歌咏比赛中,甲乙两个合唱队每场比赛得分的茎叶图如图所示(以十位数字为茎,个位数字为叶).若甲队得分的中位数是86,乙队得分的平均数是88,则 x+y= (??? )
A.?? 170???????????????????????????????????????B.?10???????????????????????????????????????C.?172???????????????????????????????????????D.?12
8.已知某地区中小学生人数和近视情况分别如图1和如图2所示,为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取 2% 的学生进行调查,则样本容量和抽取的高中生近视人数分别为(?? )
A.?100,20????????????????????????????B.?200,20????????????????????????????C.?100,10????????????????????????????D.?200,10
9.为加强学生音乐素养的培育,东莞市某高中举行“校园十大歌手”比赛,比赛现场有7名评委给选手评分,另外,学校也提前发起了网络评分,学生们可以在网络上给选手评分,场内数百名学生均参与网络评分.某选手参加比赛后,现场评委的评分表和该选手网络得分的条形图如下图所示:
评委序号
①
②
③
④
⑤
⑥
⑦
评分
10
8
9
8
9
10
9
记现场评委评分的平均分为 x1 ,网络评分的平均分为 x2 ,所有评委与场内学生评分的平均数为 x ,那么下列选项正确的是(?? )
A.?x
10.某公司在甲、乙、丙、丁四个地区分别有150,120,180,150个销售点.公司为了调查产品销售情况,需从这600个销售点中抽取一个容量为100的样本.记这项调查为①;在丙地区有20个大型销售点,要从中抽取7个调查其销售收入和售后服务等情况,记这项调查为②,则完成①,②这两项调查宜采用的抽样方法依次是( )
A.?分层抽样法,系统抽样法????????????????????????????????????B.?分层抽样法,简单随机抽样法
C.?系统抽样法,分层抽样法????????????????????????????????????D.?简单随机抽样法,分层抽样法
11.我国古代数学名著《九章算术》中有如下问题:“今有北乡8100人,西乡有7488人,南乡有6912人,现要按人数多少从三个乡共征集300人,问从各乡征集多少人”.在上述问题中,需从北乡征集的人数大约是(??? )
A.?112??????????????????????????????????????B.?108??????????????????????????????????????C.?130??????????????????????????????????????D.?168
12.已知甲、乙两组数据用茎叶图表示如图所示,若它们的中位数相同, 平均数也相同,则图中的 m,n 的比值 mn 等于( ??)
A.?38??????????????????????????????????????????B.?29??????????????????????????????????????????C.?13??????????????????????????????????????????D.?12
13.为了解某社区居民有无收看“青运会开幕式”,某记者分别从某社区 60?70 岁, 40?50 岁, 20?30 岁的三个年龄段中的 160 人, x 人, 200 人中,采用分层抽样的方法共抽查了 30 人进行调查,若在 60?70 岁这个年龄段中抽查了 8 人,那么 x 为(?? )
A.?120??????????????????????????????????????B.?180??????????????????????????????????????C.?220??????????????????????????????????????D.?240
14.下边茎叶图记录了甲、乙两组各6名学生在一次数学测试中的成绩(单位:分),已知甲组数据的众数为124,乙组数据的平均数为甲组数据的中位数,则 x,y 的值分别为(?? )
A.?4,4????????????????????????????????????B.?5,4????????????????????????????????????C.?4,5????????????????????????????????????D.?5,5
15.某公司在甲、乙、丙、丁四个地区分别有150,120,180,150个销售点.公司为了调查产品销售情况,需从这600个销售点中抽取一个容量为100的样本.按照分层抽样的方法抽取样本,则丙地区抽取的销售点比乙地区抽取的销售点多(?? )
A.?5个?????????????????????????????????????B.?8个?????????????????????????????????????C.?10个?????????????????????????????????????D.?12个
16.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是( ??)
A.?中位数??????????????????????????????????B.?平均数??????????????????????????????????C.?方差??????????????????????????????????D.?极差
17.某学校为了了解本校学生的上学方式,在全校范围内随机抽查部分学生,了解到上学方式主要有: A ——结伴步行, B ——自行乘车, C ——家人接送, D ——其他方式,并将收集的数据整理绘制成如下两幅不完整的统计图.
根据图中信息,求得本次抽查的学生中 A 类人数是(?? )
A.?30?????????????????????????????????????????B.?40?????????????????????????????????????????C.?42?????????????????????????????????????????D.?48
18.中国仓储指数是反映仓储行业经营和国内市场主要商品供求状况与变化趋势的一套指数体系.如图所示的折线图是 2017 年和 2018 年的中国仓储指数走势情况.根据该折线图,下列结论中不正确的是(??? )
A.?2018 年 1 月至 4 月的仓储指数比 2017 年同期波动性更大
B.?2017 年、 2018 年的最大仓储指数都出现在 4 月份
C.?2018 年全年仓储指数平均值明显低于 2017 年
D.?2018 年各月仓储指数的中位数与 2017 年各月仓储指数中位数差异明显
19.一支由学生组成的校乐团有男同学 48 人,女同学 36 人,若用分层抽样的方法从该乐团的全体同学中抽取 21 人参加某项活动,则抽取到的男同学人数为(? )
A.?10????????????????????????????????????????B.?11????????????????????????????????????????C.?12????????????????????????????????????????D.?13
20.已知某高中的一次测验中,甲.乙两个班级的九科平均分的雷达图如图所示,下列判断错误的是(??? )
A.?乙班的理科综合成绩强于甲班?????????????????????????????B.?甲班的文科综合成绩强于乙班
C.?两班的英语平均分分差最大????????????????????????????????D.?两班的语文平均分分差最小
二、解答题
21.“工资条里显红利,个税新政人民心”,随着2021年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革至2019年实施以来发挥巨大作用.个税新政主要内容包括:
⑴个税起征点为5000元;
⑵每月应纳税所得额(含税) = 收入-个税起征点-专项附加扣除;
⑶专项附加扣除包括住房?子女教育和赡养老人等.新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如表:
旧个税税率表(税起征点3500元)
新个税税率表(个税起征点5000元)
缴税级数
每月应纳税所得额(含税) = 收入-个税起征点
税率(%)
每月应纳税所得额(含税)=收入-个税起征点 ? 专项附加扣除
税率(%)
1
不超过1500元部分
3
不超过3000元部分
3
2
超过1500元至4500元部分
10
超过3000元至12000元部分
10
3
超过4500元至9000元的部分
20
超过12000元至25000元的部分
20
4
超过9000元至35000元的部分
25
超过25000元至35000元的部分
25
5
超过35000元至55000元部分
30
超过35000元至55000元部分
30
?
?
?
?
?
随机抽取某市1000名同一收入层级的IT从业者的相关资料,经统计分析,预估他们2021年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是 2:1:1:1 ;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等.假设该市该收入层级的IT从业者都独自享受专项附加扣除,将预估的该市该收入层级的IT从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:
(1)求该市该收入层级的IT从业者2021年月缴个税的所有可能及其概率.
(2)根据新旧个税方案,估计从2021年1月开始,经过多少个月,该市该收入层级的 IT 从业者各月少缴交的个税之和就超过2019年的月收入?
22.某企业三月中旬生产 A , B , C 三种产品共3000件,根据分层随机抽样的结果,企业统计员制作了如下的统计表格:
产品类别
A
B
C
产品数量
1300
样本中的数量
130
由于不小心,表格中 A , C 产品的有关数据已被污染得看不清楚,统计员只记得样本中 A 产品的数量比样本中 C 产品的数量多10.根据以上信息,求该企业生产 C 产品的数量.
23.? 2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间 X (单位:小时)并绘制如图所示的频率分布直方图.
(1)求这200名学生每周阅读时间的样本平均数 x 和中位数 a ( a 的值精确到0.01);
(2)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为 [6.5,7.5) , [7.5,8.5) 的学生中抽取9名参加座谈会.
(i)你认为9个名额应该怎么分配?并说明理由;
(ii)座谈中发现9名学生中理工类专业的较多.请根据200名学生的调研数据,填写下面的列联表,并判断是否有 95% 的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?
阅读时间不足8.5小时
阅读时间超过8.5小时
理工类专业
40
60
非理工类专业
附: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d) ( n=a+b+c+d ).
临界值表:
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
答案解析部分
一、单选题
1.【答案】 D
【解析】把50件产品分成5组:1—10,11—20,21—30,31—40,41—50,在第一组中用简单随机抽样抽取一个样本,然后在后面的每一组中等距离的抽取样本.
故答案为:D.
2.【答案】 B
【解析】解:平均数为 12+12+12+14+155=13 ,众数为12,差为1.
故答案为:B
3.【答案】 D
【解析】易知A,B符合题意.男生应抽取 7001200×120=70 名,女生应抽取 5001200×120=50 名.C符合题意,D不符合题意.
故答案为:D
4.【答案】 C
【解析】依题意,平均数是 80+17×(?1+3+4×2+5+7+13)=85 ,数据从小到大依次为79,83,84,84,85,87,93,故中位数为84.
故答案为:C
5.【答案】 B
【解析】根据频率分布直方图,得;∵0.02×5+0.04×5=0.3<0.5,0.3+0.08×5=0.7>0.5;
∴中位数应在20~25内,设中位数为x,则0.3+(x-20)×0.08=0.5,解得x=22.5;
∴这批产品的中位数是22.5
故答案为:B
6.【答案】 C
【解析】解:读取的前5名学生的学号依次是:39,17,37,23,35,
故答案为:C.
7.【答案】 D
【解析】由茎叶图知,甲的中位数为 80+x=86 ,故 x=6 ;
乙的平均数为 78+82+80+y+89+91+93+977=88 ,
解得 y=6 ,所以 x+y=12 .
故答案为:D.
8.【答案】 B
【解析】由题意知,样本容量为 (3500+4500+2000)×2%=200 ,其中高中生人数为 2000×2%=40 ,
高中生的近视人数为 40×50%=20 ,
故答案为:B.
9.【答案】 C
【解析】 x1=10+8+9+8+9+10+97=9 , x2=0.1×7+0.1×8+0.2×9+0.6×10=9.3 ,
则 x1+x22=9.15 ,设场内学生人数为 a(a>100) ,
则 x=9.3a+63a+7=9.3(a+7)?2.1a+7=9.3?2.1a+7 ,
因为 a>100 ,
所以 x=9.3?2.1a+7>9.3?2.1107≈9.28>x1+x22 ,
故答案为:C.
10.【答案】 B
【解析】依据题意,第①项调查中,总体中的个体差异较大,应采用分层抽样法;第②项调查总体中个体较少,应采用简单随机抽样法.
故答案为:B.
11.【答案】 B
【解析】由题,则 300×81008100+7488+6912=108 ,
故答案为:B
12.【答案】 A
【解析】甲组数据: 27,30+m,39 ,中位数为 30+m ,
乙组数据: 20+n,32,34,38 ,中位数为: 32+342=33 ,
所以 x甲=27+(30+m)+393=96+m3,x乙=(20+n)+32+34+384=124+n4 ,
所以 {30+m=33,96+m3=124+n4?{m=3,n=8,?mn=38 ,
故答案为:A.
13.【答案】 D
【解析】由题得 30160+x+200=8160 ,
所以x=240.
故答案为:D
14.【答案】 C
【解析】因为甲组数据的众数是124,所以 x=4 .因为乙组数据的平均数等于甲组数据的中位数,即124.所以 124×6?114?118?122?127?138=125 ,所以 y=5 .
故答案为:C.
15.【答案】 C
【解析】由题意
乙地区抽取 120600×100=20 (个)
丙地区抽取 180600×100=30 (个)
30?20=10 (个)
丙地区抽取的销售点比乙地区抽取的销售点多10个;
故答案为: C
16.【答案】 A
【解析】A项,中位数是以通过排序后的最中间一位数,不受最大、最小两个极端数值的影响。故A项正确,符合题意。B项,平均数是指一组数据之和再除以数据的个数,因此不论哪一个数据的变化都有可能影响一组数据的平均数,故B项错误。C项,方差是各个数据与平均数之差的平方的平均数。因此一组数据中的任何一个数据的变化都有可能使方差变化,故C项错误。D项,极差是指最大值减最小值后所得的数值,题中将最大,最小值除去了,故有可能影响数据的极差,故D项错误。
故答案为:A
17.【答案】 A
【解析】解:根据选择D方式的有18人,所占比例为15%,得总人数为 1815%= 120人,故选择A方式的人数为120﹣42﹣30﹣18=30人.
故答案为:A.
18.【答案】 D
【解析】对于A,由图可得 2017 年 1 月至 4 月的仓储指数变化平缓,而 2018 年 1 月至 4 月的仓储指数的波动较大,所以A符合题意.
对于B,由图可得 2017 年、 2018 年的最大仓储指数都出现在 4 月份,所以B符合题意.
对于C,由图可得4月份两年的仓储指数相同,9月、11月、12月的仓储指数2018年比2017年低,其余个月份都是2018年的低,并且有明显的差异,所以 2018 年全年仓储指数平均值明显低于 2017 年,所以C符合题意.
对于D,由图中的数据可得两年的仓储指数的中位数都在51.5左右,差别不大,所以D不正确.
故答案为:D.
19.【答案】 C
【解析】用分层抽样的方法从校乐团中抽取 21 人,所得抽样比为 2148+36=14 ,因此抽取到的男同学人数为 48×14=12 人.
故答案为:C
20.【答案】 D
【解析】由甲、乙两个班级的九科平均分的雷达图可得:
乙班的理科综合成绩强于甲班,即选项 A 正确,
甲班的文科综合成绩强于乙班,即选项 B 正确,
两班的英语平均分分差最大,即选项 C 正确,
两班地理平均分分差最小,即选项 D 错误,
故答案为:D.
二、解答题
21.【答案】 (1)解:由题意,既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是 2:1:1:1 .
①既不符合子女教育扣除又不符合赡养老人扣除的人群每月应纳税所得额为
24000?5000?1000=18000 元,
月缴个税为 3000×0.03+9000×0.1+6000×0.2=2190 元,其概率为 25 ;
②只符合子女教育扣除但不符合赡养老人扣除的人群每月应纳税所得额为
24000?5000?1000?1000=17000 元,
月缴个税为 3000×0.03+9000×0.1+5000×0.2=1990 元,其概率为 15 ;
③只符合赡养老人扣除但不符合子女教育扣除的人群每月应纳税所得额为 24000?5000?1000?2000=16000 元,
月缴个税为 3000×0.03+9000×0.1+4000×0.2=1790 元,其概率为 15 ;
④既符合子女教育扣除又符合赡养老人扣除的人群每月应纳税所得额为 24000?5000?1000?1000?2000=15000 元,
月缴个税为 3000×0.03+9000×0.1+3000×0.2=1590 元,其概率为 15 ;
(2)解:在旧政策下,该收入阶层的 IT 从业者每月应纳税所得额为 24000?3500=20500 元,
故月缴个税为 1500×0.03+3000×0.1+4500×0.2+11500×0.25=4120 元,
在新政策下,该收入阶层的 IT 从业者每月应纳税所得额为 2190×25+(1990+1790+1590)×15=1950 元,
每月少缴个税 4120?1950=2170 元,
设经过 x 个月该市该收入阶层的 IT 从业者各月少缴交的个税之和就超过2019年的月收入,
则 2170x≥24000 ,又 x∈N ,解得 x≥12(x∈N) ,
所以经过12个月,该市该收入阶层的 IT 从业者各月少缴交的个税之和就超过2019年的月收入.
【解析】 (1)根据题中给出的信息,分四种情况按照条件中的计算公式分别求出月缴个税即可;
(2)计算两种政策下的每月应缴个税额度差,然后列出不等式,求解即可得到答案.
22.【答案】 解:设样本量为 x ,
则 x3000×1300=130 ,
∴x=300 ,
∴ 在样本中 A 产品和 C 产品共有 300?130=170 (件).
设样本中 C 产品数量为 y ,则 y+y+10=170 ,
∴y=80 ,
∴ 该企业生产 C 产品的数量为 3000300×80=800 .
【解析】根据题意由分层抽样的定义代入数值计算出结果即可。
?
23.【答案】 (1)解:该组数据的平均数 x=6×0.03+7×0.1+8×0.2+9×0.35+10×0.19 +11×0.09+12×0.04=9 ,
因为 0.03+0.1+0.2+0.35=0.68>0.5 ,所以中位数 a∈[8.5,9.5) ,
由 0.03+0.1+0.2+(a?8.5)×0.35=0.5 ,解得 a=0.5?0.330.35+8.5≈8.99
(2)解:(i)每周阅读时间为 [6.5,7.5) 的学生中抽取3名,每周阅读时间为 [7.5,8.5) 的学生中抽取6名.
理由:每周阅读时间为 [6.5,7.5) 与每周阅读时间为 [7.5,8.5) 是差异明显的两层,为保持样本结构与总体结构的一致性,提高样本的代表性,宜采用分层抽样的方法抽取样本;因为两者频率分别为0.1,0.2,所以按照 1:2 进行名额分配.
(ii)由频率分布直方图可知,阅读时间不足8.5小时的学生共有 200×(0.03+0.1+0.2)=66 人,超过8.5小时的共有 200?66=134 人.
于是列联表为:
阅读时间不足8.5小时
阅读时间超过8.5小时
理工类专业
40
60
非理工类专业
26
74
K2 的观测值 k=200×(40×74?26×60)266×134×100×100≈4.432>3.841 ,
所以有 95% 的把握认为学生阅读时间不足与“是否理工类专业”有关
【解析】(1)根据平均数,中位数的定义进行求解即可(2)完成列联表,计算 K2 的观测值,结合独立性检验的性质进行判断即可.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
