9.2用样本估计总体、9.3统计案例 公司员工的肥胖情况调查分 基础练习-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析)
文档属性
| 名称 | 9.2用样本估计总体、9.3统计案例 公司员工的肥胖情况调查分 基础练习-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 183.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-04 00:00:00 | ||
图片预览




文档简介
9.2 用样本估计总体--9.3统计案例 公司员工的肥胖情况调查分 基础练习
一、单选题
1.2020年12月31日,国务院联防联控机制发布,国药集团中国生物的新冠病毒灭活疫苗已获药监局批准附条件上市,其保护效力达到世界卫生组织及药监局相关标准要求,现已对18至59岁的人提供.根据某地接种年龄样本的频率分布直方图(如图)估计该地接种年龄的中位数为(??? )
A.?40?????????????????????????????????????????B.?39?????????????????????????????????????????C.?38?????????????????????????????????????????D.?37
2.甲、乙两名射击运动爱好者在相同条件下各射击10次,中靶环数情况如图所示.则甲、乙两人中靶环数的方差分别为(?? )
A.?7,7???????????????????????????????B.?7,1.2???????????????????????????????C.?1.1,2.3???????????????????????????????D.?1.2,5.4
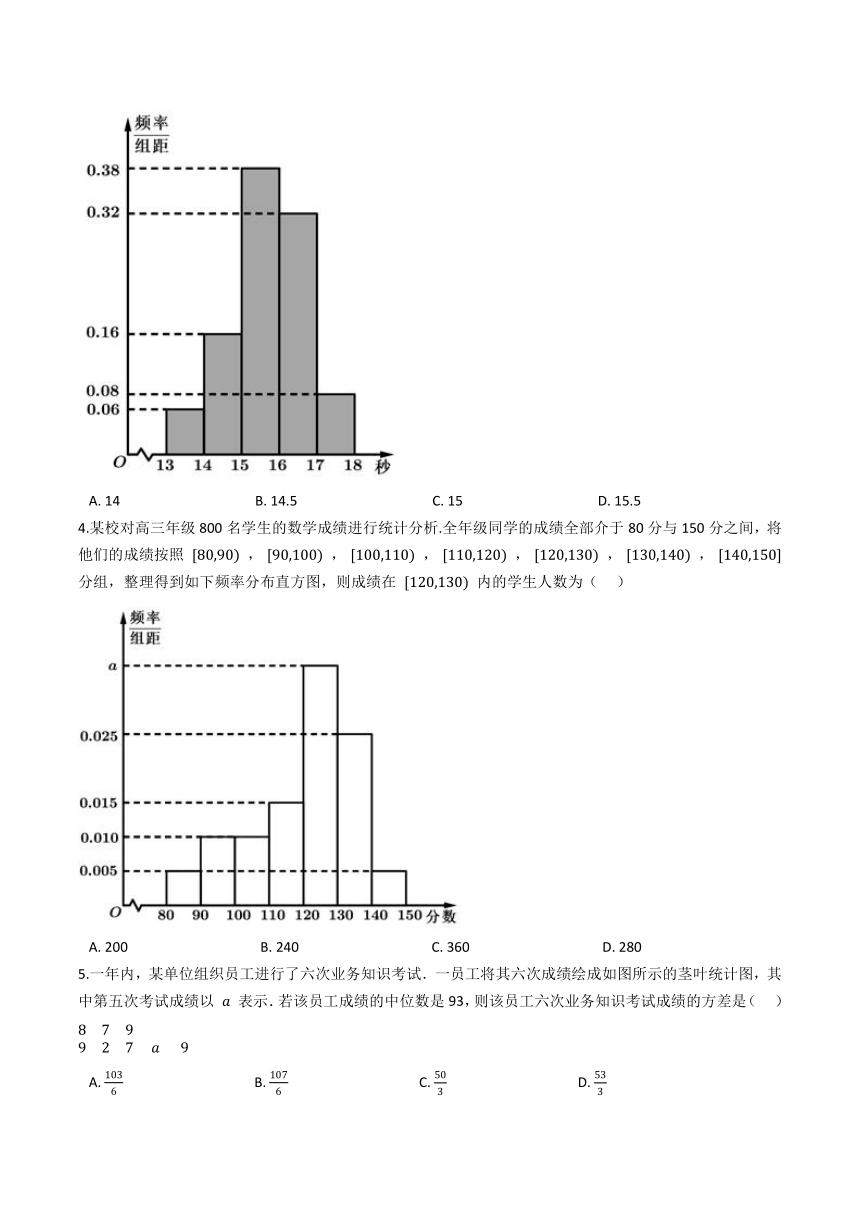
3.某校抽取100名学生做体能测认,其中百米测试中,成绩全部介于13秒与18秒之间,将测试结果分成五组:第一组 [13,14) ,第二组 [14,15) , ? ,第五组 [17,18] .如图是按上述分组方法得到的频率分布直方图,若成绩低于 a 即为优秀,如果优秀的人数为14人,则 a 的估计值是( ??)
A.?14???????????????????????????????????????B.?14.5???????????????????????????????????????C.?15???????????????????????????????????????D.?15.5
4.某校对高三年级800名学生的数学成绩进行统计分析.全年级同学的成绩全部介于80分与150分之间,将他们的成绩按照 [80,90) , [90,100) , [100,110) , [110,120) , [120,130) , [130,140) , [140,150] 分组,整理得到如下频率分布直方图,则成绩在 [120,130) 内的学生人数为(??? )
A.?200??????????????????????????????????????B.?240??????????????????????????????????????C.?360??????????????????????????????????????D.?280
5.一年内,某单位组织员工进行了六次业务知识考试.一员工将其六次成绩绘成如图所示的茎叶统计图,其中第五次考试成绩以 a 表示.若该员工成绩的中位数是93,则该员工六次业务知识考试成绩的方差是(??? )
879927a9
A.?1036??????????????????????????????????????B.?1076??????????????????????????????????????C.?503??????????????????????????????????????D.?533
6.设一组样本数据x1 , x2 , …,xn的方差为0.01,则数据10x1 , 10x2 , …,10xn的方差为(??? )
A.?0.01????????????????????????????????????????B.?0.1????????????????????????????????????????C.?1????????????????????????????????????????D.?10
7.将一个容量为1000的样本分成若干组,已知某组的频率为0.4,则该组的频数是(??? )
A.?4????????????????????????????????????????B.?40????????????????????????????????????????C.?250????????????????????????????????????????D.?400
8.新中国成立70周年以来,党中央、国务院高度重视改善人民生活,始终把脱贫致富和提高人民生活水平作为一切工作的出发点和落脚点新疆某地区为了带动当地经济发展,大力发展旅游业,如图是2015—2019年到该地区旅游的游客数量(单位:万人次)的变化情况,则下列结论错误的是( ???)
A.?2015—2019年到该地区旅游的人数与年份成正相关
B.?2019年到该地区旅游的人数是2015年的12倍
C.?2016—2019年到该地区旅游的人数平均值超过了220万人次
D.?从2016年开始,与上一年相比,2019年到该地区旅游的人数增加得最多
9.现对 A,B 有如下观测数据
A
3
4
5
6
7
B
16
15
13
14
17
记本次测试中, A,B 两组数据的平均成绩分别为 xA,xB , A,B 两班学生成绩的方差分别为 SA2 , SB2 ,则(??? )
A.?xAxB , SA2xB , SA2=SB2
10.为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在2015 年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为 70% .2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
实施项目
种植业
养殖业
工厂就业
服务业
参加用户比
40%
40%
10%
10%
脱贫率
95%
95%
90%
90%
那么 2019 年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的(?? )
A.?2728 倍????????????????????????????????B.?4735 倍????????????????????????????????C.?4835 倍????????????????????????????????D.?75 倍
11.甲、乙两名射击运动员分别进行了5次射击训练,成绩(单位:环)如下:
甲:7,8,8,8,9??? 乙:6,6,7,7,10;
若甲、乙两名运动员的平均成绩分别用 x1,x2 表示,方差分别为 S12,S22 表示,则(??? )
A.?x1>x2,s12>s22????????????????B.?x1>x2,s12s22
12.已知某地区中小学生人数和近视情况分别如图甲和图乙所示.为了了解该地区中小学生的近视形成原因用分层抽样的方法抽取 2% 的学生进行调查,则样本容量和抽取的高中生近视人数分别为(??? )
?
A.?100,40????????????????????????????B.?100,20????????????????????????????C.?200,40????????????????????????????D.?200,20
13.为了解一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:㎝).根据所得数据画出的样本频率分布直方图如图,那么在这片树木中,底部周长小于110㎝的株树大约是( ??)
A.?3000???????????????????????????????????B.?6000
???????????????????????????????????C.?7000???????????????????????????????????D.?8000
14.若样本 1+x1,1+x2,1+x3,?,1+xn 的平均数是10,方差为2,则对于样本 2+2x1,2+2x2,2+2x3,?,2+2xn ,下列结论正确的是(??? )
A.?平均数为20,方差为4????????????????????????????????????????B.?平均数为11,方差为4
C.?平均数为21,方差为8????????????????????????????????????????D.?平均数为20,方差为8
15.假设有一个专养草鱼的池塘,现要估计池塘内草鱼的数量.第一步,从池塘内打捞一批草鱼,做上标记,然后将其放回池塘,第二步,再次打捞一批草鱼,根据其中做标记的草鱼数量估计整个池塘中草鱼的数量.假设第一次打捞的草鱼有50尾,第二次打捞的草鱼总数为50尾,其中有标记的为7尾,试估计整个池塘中草鱼的数量大约为(??? )
A.?250??????????????????????????????????????B.?350??????????????????????????????????????C.?450??????????????????????????????????????D.?550
16.已知一个样本为x,1,y,5,其中x,y是方程组 {x+y=2x2+y2=10 的解,则这个样本的标准差是(?? )
A.?2?????????????????????????????????????????B.?5?????????????????????????????????????????C.?2?????????????????????????????????????????D.?5
17.已知一组数据 x1,x2,x3…,xn ,的平均数为5,方差为2,则数据 3x1+1 , 3x2+1 ,…, 3xn+1 的平均数 x 与方差 s2 三分别为(??? )
A.?x=15 , s2=6???????????B.?x=16 , s2=7???????????C.?x=16 , s2=18???????????D.?x=16 , s2=19
18.一个频率分布表(样本容量为 50 )不小心被损坏了一部分,只记得样本中数据在 [20,60) 上的频率为 0.6 ,则估计样本在 [40,60) 内的数据个数为(?? )
分组
[10,20)
[20,30)
[30,40)
频数
5
7
8
A.?10????????????????????????????????????????B.?13????????????????????????????????????????C.?14????????????????????????????????????????D.?15
19.近年来随着我国在教育科研上的投入不断加大,科学技术得到迅猛发展,国内企业的国际竞争力得到大幅提升.某品牌公司一直默默拓展海外市场,在海外设了多个分支机构,现需要国内公司外派大量中青年员工.该企业为了解这两个年龄层员工是否愿意被外派工作的态度,按分层抽样的方式从中青年员工中随机调查了 100 位,得到数据如下表:
?
愿意被外派
不愿意被外派
合计
中年员工
20
20
40
青年员工
40
20
60
合计
60
40
100
由 K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d) 并参照附表,得到的正确结论是(??? )
附表:
P(K2≥k0)
0.10
0.01
0.001
k0
2.706
6.635
10.828
A.?在犯错误的概率不超过10%的前提下,认为 “是否愿意外派与年龄有关”
B.?在犯错误的概率不超过10%的前提下,认为 “是否愿意外派与年龄无关”
C.?有99% 以上的把握认为“是否愿意外派与年龄有关”
D.?有99% 以上的把握认为“是否愿意外派与年龄无关”
20.某公司2018年在各个项目中总投资500万元,下图是几类项目的投资占比情况,已知在1万元以上的项目投资中,少于3万元的项目投资占 821 ,那么不少于3万元的项目投资共有(?? )
A.?56万元?????????????????????????????B.?65 万元?????????????????????????????C.?91 万元?????????????????????????????D.?147 万元
二、解答题
21.某教练统计了甲、乙两名三级跳远运动员连续5次的跳远成绩(单位:米),统计数据如图所示.
(1)分别求甲、乙跳远成绩的平均数;
(2)通过平均数和方差分析甲、乙两名运动员的平均水平和发挥的稳定性.
22.自从新冠肺炎疫情暴发以来,各地都采取积极有效的防控措施,使疫情得到了有效的控制.某地对100名年龄在 [20,45] 岁,患病后已经康复的居民做了数据统计,绘成如图所示不完整的频率分布直方图.统计员在绘制频率分布直方图的过程中所搜集的数据只能确定年龄在 [30,35) 与 [40,45] 的新冠肺炎康复人数之和是年龄在 [35,40) 的新冠肺炎康复人数的3倍,且 [30,35) 组的频率比 [40,45] 组的频率多0.15.
(1)分别求 [30,35) , [35,40) , [40,45] 组对应的频率;
(2)求年龄在 [35,45] 的新冠肺炎康复人数.
23.某种产品的质量用其质量指标值来衡量)质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为 A 配方和 B 配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A 配方的频数分布表:
指标值分组
[90,94)
[94,98)
[98,102)
[102,106)
[106,110]
频数
8
20
42
22
8
B 配方的频数分布表:
指标值分组
[90,94)
[94,98)
[98,102)
[102,106]
[106,110]
频数
4
12
42
32
10
(1)分别估计用 A 配方、 B 配方生产的产品的优质品率;
(2)已知用 B 配方生产的一件产品的利润(单位:元)与其质量指标值 t 的关系为 y={?2,t<942,94≤t<1024,t≥102 ,估计用 B 配方生产的一件产品的利润大于 0 的概率,并求用 B 配方生产的上述 100 件产品的平均利润.
答案解析部分
一、单选题
1.【答案】 C
【解析】年龄位于 [18,24) 的频率为 0.013×6=0.078 ,
年龄位于 [24,30) 的频率为 0.023×6=0.138 ,
年龄位于 [30,36) 的频率为 0.034×6=0.204 ,
年龄位于 [36,42) 的频率为 0.040×6=0.240 ,
因为 0.078+0.138+0.204=0.42<0.5 ,而
0.078+0.138+0.204+0.240=0.42=0.66>0.5 ,
所以中位数位于 [36,42) ,设中位数为 x ,
则 0.078+0.138+0.204+(x?36)×0.04=0.5 ,
解得: x=38 ,
故答案为:C.
2.【答案】 D
【解析】实线的数字为: 2,4,6,8,7,7,8,9,9,10 ,
虚线的数字为: 9,5,7,8,7,6,8,6,7,7 ,
所以 x乙=110(2+4+6+8+7+7+8+9+9+10)=7 ,
x甲=110(9+5+7+8+7+6+8+6+7+7)=7 ,
S甲2=110[(9-7)2+(5-7)2+(7?7)2+(8?7)2+?+(7?7)2]=1.2
S乙2=110[(2-7)2+(4-7)2+(6?7)2+(8?7)2+?+(10?7)2]=5.4 .
故答案为:D
3.【答案】 B
【解析】优秀人数所占的频率为 14100=0.14 ,
测试结果位于 [13,14) 的频率为 0.06<0.14 ,测试结果位于 [13,15) 的频率为 0.06+0.16<0.14 ,所以, a∈(14,15) ,
由题意可得 0.06+(a?14)×0.16=0.14 ,解得 a=14.5 。
故答案为:B.
4.【答案】 B
【解析】从全体学生中根据成绩采用分层抽样的方法抽取800名同学的试卷进行分析, 则从成绩在 [120,130) 内的学生中抽取的人数为:
800 ×[1 ?(0.005+0.010+0.010+0.015+0.025 +0.005)×10]=240。
故答案为: B
5.【答案】 D
【解析】 ∵ 该员工成绩的中位数是 93 , ∴92+90+a2=93 ,解得: a=4 .
∴x=87+89+92+97+94+996=93 ,
∴ 该员工六次业务知识考试成绩的方差: s2=16[(87?93)2+(89?93)2+ (92?93)2+(97?93)2+(94?93)2 +(99?93)2]=1066=533 .
故答案为:D.
6.【答案】 C
【解析】因为数据 axi+b,(i=1,2,?,n) 的方差是数据 xi,(i=1,2,?,n) 的方差的 a2 倍,
所以所求数据方差为 102×0.01=1
故答案为:C
7.【答案】 D
【解析】 ∵ 一个容量为1000的样本分成若干组,某组的频率为0.4,
∴ 该组的频数为: 1000×0.4=400 .
故答案为:D.
8.【答案】 C
【解析】解:对于A,观察统计图可知,A符合题意;
对于B,2019年到该地区旅游的人数是2015年的 36030=12 (倍),所以B符合题意;
对于C,2016—2019年到该地区旅游的人数平均值为 14(100+160+230+360)=212.5 (万人次),C不符合题意;
对于D,由图可知,与上一年相比,2019年到该地区旅游的人数增加得最多,D符合题意;
故答案为:C
9.【答案】 C
【解析】 xA=3+4+5+6+75=5 , xB=16+15+13+14+175=15 ,
(3?5)2+(4?5)2+(5?5)2+(6?5)2+(7?5)25=2 ,
SB2=(16?15)2+(15?15)2+(13?15)2+(14?15)2+(17?15)25=2 ,故 xA故答案为:C
10.【答案】 B
【解析】设贫困户总数为 a ,脱贫率 P=2×4000×9500a+2×1000×9000aa=9400 ,
所以 94007000=4735 .
故 2019 年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的 4735 倍.
故答案为:B
11.【答案】 B
【解析】 x1=7+8+8+8+95=8 , x2=6+6+7+7+105=7.2 ,故 x1>x2 .
s12=(7?8)2+(8?8)2+(8?8)2+(8?8)2+(9?8)25=0.4 ;
s22=(6?7.2)2+(6?7.2)2+(7?7.2)2+(7?7.2)2+(10?7.2)25=2.16 ,故 s12故答案为:B.
12.【答案】 D
【解析】由图甲可知,学生总数为 4500+3500+2000=10000 (人),
故抽取的样本容量为 10000×2%=200 (人),
其中抽取的高中学生有 200×200010000=40 (人);
由图乙可知,高中生近视率为 50% ,
∴抽取的高中生近视人数为 40×50%=20 (人).
故答案为:D.
13.【答案】 C
【解析】由频率分布直方图可得,样本中底部周长小于110㎝的概率为 (0.001+0.002+0.004)×10=0.7 ,
因此在这片树木中,底部周长小于110㎝的株树大约是 10000×0.7=7000 .
故答案为:C.
14.【答案】 D
【解析】样本 1+x1,1+x2,1+x3,?,1+xn 的平均数是10,方差为2,
所以样本 2+2x1,2+2x2,2+2x3,?,2+2xn 的平均数为 2×10=20 ,方差为 22×2=8 .
故选:D.
15.【答案】 B
【解析】设池塘中草鱼的数量大约为 x ,可得 50x=750 ,
所以 x≈357 ,所以池塘中草鱼大约有 350 条.
故答案为:B.
16.【答案】 D
【解析】根据题意,x,y是方程组 {x+y=2x2+y2=10 的解,
则样本x,1,y,5中,有x+1+y+5=(x+y)+1+5=8,其平均数 x=x+1+y+54=2
其方差s2 =14× [12+x2+y2+52﹣4 ×x 2]=5,
则标准差s =5 ,
故答案为:D.
.
17.【答案】 C
【解析】由题, 1n(x1+x2+x3…+xn)=5 , 1n[(x1?5)2+(x2?5)2+...+(xn?5)2]=2 .
故 x=1n(3x1+1+3x2+1+3x3+1…+3xn+1)=1n[3(x1+x2+x3…+xn)+n]
=3×1n(x1+x2+x3…+xn)+1=3×5+1=16 .即 x=16 .
s2=1n[(3x1+1?16)2+(3x2+1?16)2+...+(3xn+1?16)2]
=1n[9(x1?5)2+9(x2?5)2+...+9(xn?5)2]
=9×1n[(x1?5)2+(x2?5)2+...+(xn?5)2]=18 .即 s2=18
故答案为:C
18.【答案】 D
【解析】设样本在 [40,60) 内的数据个数为x,
则 7+8+x50=0.6 ,
所以x=15.
故答案为:D
19.【答案】 A
【解析】由题可得: K2=100(20×20?40×20)260×40×60×40=100×400×40060×40×60×40≈2.778>2.706
故在犯错误的概率不超过10%的前提下,认为 “是否愿意外派与年龄有关”, 有90% 以上的把握认为“是否愿意外派与年龄有关,所以答案选A;
故答案为:A
20.【答案】 B
【解析】由图可知,1万元以上的项目投资占:1-0.46-0.33=0.21=21%,500×0.21=105,
少于3万元的项目投资占 821 ,则不少于3万元的项目投资占 1321
105× 1321 =65万元,
故答案为:B.
二、解答题
21.【答案】 (1)解:根据题意可知 x甲=15(8+9+12+12+14)=11 ,
x乙=15(7+9+11+13+15)=11
(2)解: s甲2=15[(8?11)2+(9?11)2+(12?11)2 +(12?11)2+(14?11)2]=4.8 ,
s乙2=15[(7?11)2+(9?11)2+(11?11)2 +(13?11)2+(15?11)2]=8 .
∵x甲=x乙 , s甲2∴ 甲、乙两名运动员的平均水平相当,甲的发挥更稳定
【解析】(1)利用平均数的定义直接求解即可;
(2)利用方差公式求出甲、乙两名运动员的方差,利用方差越小数据越稳定判断即可。
?
?
22.【答案】 (1)解:由频率分布直方图,得 [20,25) 组对应的频率为 0.01×5=0.05 , [25,30) 组对应的频率为 0.07×5=0.35 .
设 [30,35) , [35,40) , [40,45] 组对应的频率分别为 x , y , z ,则
{x+y+z=1?0.05?0.35x+z=3yx?z=0.15 ,解得 {x=0.3y=0.15z=0.15
(2)解:因为 [35,45] 对应的频率为 0.15+0.15=0.3 ,
所以年龄在 [35,45] 的新冠肺炎康复人数为 100×0.3=30
【解析】(1) 由频率分布直方图,得?[20,25)?组对应的频, 设?[30,35)? , ?[35,40)? , ?[40,45]?组对应的频率分别为?x? , ?y? , ?z? , 依题意得到方程组,解得即可;
(2)首先求出 ?[35,45] 对应的频率,即可求出康复人数。
?
?
23.【答案】 (1)解: ∵ 由试验结果知,用 A 配方生产的产品中优质品的频率为 22+8100=0.3
∴ ?用 A 配方生产的产品中优质品率的估计值为 0.3
∵ 由试验结果知,用 B 配方生产的产品中优质品的频率为 32+10100=0.42
∴ 用 B 配方生产的产品中优质品率的估计值为 0.42
(2)解:由条件知,用 B 配方生产的一件产品的利润大于 0 当且仅当其质量指标值 t≥94
由试验结果知,质量指标值 t≥94 的频率为 0.96 .
∴ 用 B 配方生产的一件产品的利润大于 0 的概率约为 0.96 .
用 B 配方生产的 100 件产品的平均利润为 1100×[4×(?2)+54×2+42×4]=2.68 (元).
【解析】(1)根据某种产品的质量用其质量指标值来衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品,根据评论计算公式即可求得答案.(2)由条件知,用 B 配方生产的一件产品的利润大于 0 当且仅当其质量指标值 t≥94 ,由试验结果知,质量指标值 t≥94 的频率为 0.96 ,用 B 配方生产的一件产品的利润大于 0 的概率约为 0.96 ,即可求得答案.
一、单选题
1.2020年12月31日,国务院联防联控机制发布,国药集团中国生物的新冠病毒灭活疫苗已获药监局批准附条件上市,其保护效力达到世界卫生组织及药监局相关标准要求,现已对18至59岁的人提供.根据某地接种年龄样本的频率分布直方图(如图)估计该地接种年龄的中位数为(??? )
A.?40?????????????????????????????????????????B.?39?????????????????????????????????????????C.?38?????????????????????????????????????????D.?37
2.甲、乙两名射击运动爱好者在相同条件下各射击10次,中靶环数情况如图所示.则甲、乙两人中靶环数的方差分别为(?? )
A.?7,7???????????????????????????????B.?7,1.2???????????????????????????????C.?1.1,2.3???????????????????????????????D.?1.2,5.4
3.某校抽取100名学生做体能测认,其中百米测试中,成绩全部介于13秒与18秒之间,将测试结果分成五组:第一组 [13,14) ,第二组 [14,15) , ? ,第五组 [17,18] .如图是按上述分组方法得到的频率分布直方图,若成绩低于 a 即为优秀,如果优秀的人数为14人,则 a 的估计值是( ??)
A.?14???????????????????????????????????????B.?14.5???????????????????????????????????????C.?15???????????????????????????????????????D.?15.5
4.某校对高三年级800名学生的数学成绩进行统计分析.全年级同学的成绩全部介于80分与150分之间,将他们的成绩按照 [80,90) , [90,100) , [100,110) , [110,120) , [120,130) , [130,140) , [140,150] 分组,整理得到如下频率分布直方图,则成绩在 [120,130) 内的学生人数为(??? )
A.?200??????????????????????????????????????B.?240??????????????????????????????????????C.?360??????????????????????????????????????D.?280
5.一年内,某单位组织员工进行了六次业务知识考试.一员工将其六次成绩绘成如图所示的茎叶统计图,其中第五次考试成绩以 a 表示.若该员工成绩的中位数是93,则该员工六次业务知识考试成绩的方差是(??? )
879927a9
A.?1036??????????????????????????????????????B.?1076??????????????????????????????????????C.?503??????????????????????????????????????D.?533
6.设一组样本数据x1 , x2 , …,xn的方差为0.01,则数据10x1 , 10x2 , …,10xn的方差为(??? )
A.?0.01????????????????????????????????????????B.?0.1????????????????????????????????????????C.?1????????????????????????????????????????D.?10
7.将一个容量为1000的样本分成若干组,已知某组的频率为0.4,则该组的频数是(??? )
A.?4????????????????????????????????????????B.?40????????????????????????????????????????C.?250????????????????????????????????????????D.?400
8.新中国成立70周年以来,党中央、国务院高度重视改善人民生活,始终把脱贫致富和提高人民生活水平作为一切工作的出发点和落脚点新疆某地区为了带动当地经济发展,大力发展旅游业,如图是2015—2019年到该地区旅游的游客数量(单位:万人次)的变化情况,则下列结论错误的是( ???)
A.?2015—2019年到该地区旅游的人数与年份成正相关
B.?2019年到该地区旅游的人数是2015年的12倍
C.?2016—2019年到该地区旅游的人数平均值超过了220万人次
D.?从2016年开始,与上一年相比,2019年到该地区旅游的人数增加得最多
9.现对 A,B 有如下观测数据
A
3
4
5
6
7
B
16
15
13
14
17
记本次测试中, A,B 两组数据的平均成绩分别为 xA,xB , A,B 两班学生成绩的方差分别为 SA2 , SB2 ,则(??? )
A.?xA
10.为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在2015 年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为 70% .2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
实施项目
种植业
养殖业
工厂就业
服务业
参加用户比
40%
40%
10%
10%
脱贫率
95%
95%
90%
90%
那么 2019 年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的(?? )
A.?2728 倍????????????????????????????????B.?4735 倍????????????????????????????????C.?4835 倍????????????????????????????????D.?75 倍
11.甲、乙两名射击运动员分别进行了5次射击训练,成绩(单位:环)如下:
甲:7,8,8,8,9??? 乙:6,6,7,7,10;
若甲、乙两名运动员的平均成绩分别用 x1,x2 表示,方差分别为 S12,S22 表示,则(??? )
A.?x1>x2,s12>s22????????????????B.?x1>x2,s12
12.已知某地区中小学生人数和近视情况分别如图甲和图乙所示.为了了解该地区中小学生的近视形成原因用分层抽样的方法抽取 2% 的学生进行调查,则样本容量和抽取的高中生近视人数分别为(??? )
?
A.?100,40????????????????????????????B.?100,20????????????????????????????C.?200,40????????????????????????????D.?200,20
13.为了解一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:㎝).根据所得数据画出的样本频率分布直方图如图,那么在这片树木中,底部周长小于110㎝的株树大约是( ??)
A.?3000???????????????????????????????????B.?6000
???????????????????????????????????C.?7000???????????????????????????????????D.?8000
14.若样本 1+x1,1+x2,1+x3,?,1+xn 的平均数是10,方差为2,则对于样本 2+2x1,2+2x2,2+2x3,?,2+2xn ,下列结论正确的是(??? )
A.?平均数为20,方差为4????????????????????????????????????????B.?平均数为11,方差为4
C.?平均数为21,方差为8????????????????????????????????????????D.?平均数为20,方差为8
15.假设有一个专养草鱼的池塘,现要估计池塘内草鱼的数量.第一步,从池塘内打捞一批草鱼,做上标记,然后将其放回池塘,第二步,再次打捞一批草鱼,根据其中做标记的草鱼数量估计整个池塘中草鱼的数量.假设第一次打捞的草鱼有50尾,第二次打捞的草鱼总数为50尾,其中有标记的为7尾,试估计整个池塘中草鱼的数量大约为(??? )
A.?250??????????????????????????????????????B.?350??????????????????????????????????????C.?450??????????????????????????????????????D.?550
16.已知一个样本为x,1,y,5,其中x,y是方程组 {x+y=2x2+y2=10 的解,则这个样本的标准差是(?? )
A.?2?????????????????????????????????????????B.?5?????????????????????????????????????????C.?2?????????????????????????????????????????D.?5
17.已知一组数据 x1,x2,x3…,xn ,的平均数为5,方差为2,则数据 3x1+1 , 3x2+1 ,…, 3xn+1 的平均数 x 与方差 s2 三分别为(??? )
A.?x=15 , s2=6???????????B.?x=16 , s2=7???????????C.?x=16 , s2=18???????????D.?x=16 , s2=19
18.一个频率分布表(样本容量为 50 )不小心被损坏了一部分,只记得样本中数据在 [20,60) 上的频率为 0.6 ,则估计样本在 [40,60) 内的数据个数为(?? )
分组
[10,20)
[20,30)
[30,40)
频数
5
7
8
A.?10????????????????????????????????????????B.?13????????????????????????????????????????C.?14????????????????????????????????????????D.?15
19.近年来随着我国在教育科研上的投入不断加大,科学技术得到迅猛发展,国内企业的国际竞争力得到大幅提升.某品牌公司一直默默拓展海外市场,在海外设了多个分支机构,现需要国内公司外派大量中青年员工.该企业为了解这两个年龄层员工是否愿意被外派工作的态度,按分层抽样的方式从中青年员工中随机调查了 100 位,得到数据如下表:
?
愿意被外派
不愿意被外派
合计
中年员工
20
20
40
青年员工
40
20
60
合计
60
40
100
由 K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d) 并参照附表,得到的正确结论是(??? )
附表:
P(K2≥k0)
0.10
0.01
0.001
k0
2.706
6.635
10.828
A.?在犯错误的概率不超过10%的前提下,认为 “是否愿意外派与年龄有关”
B.?在犯错误的概率不超过10%的前提下,认为 “是否愿意外派与年龄无关”
C.?有99% 以上的把握认为“是否愿意外派与年龄有关”
D.?有99% 以上的把握认为“是否愿意外派与年龄无关”
20.某公司2018年在各个项目中总投资500万元,下图是几类项目的投资占比情况,已知在1万元以上的项目投资中,少于3万元的项目投资占 821 ,那么不少于3万元的项目投资共有(?? )
A.?56万元?????????????????????????????B.?65 万元?????????????????????????????C.?91 万元?????????????????????????????D.?147 万元
二、解答题
21.某教练统计了甲、乙两名三级跳远运动员连续5次的跳远成绩(单位:米),统计数据如图所示.
(1)分别求甲、乙跳远成绩的平均数;
(2)通过平均数和方差分析甲、乙两名运动员的平均水平和发挥的稳定性.
22.自从新冠肺炎疫情暴发以来,各地都采取积极有效的防控措施,使疫情得到了有效的控制.某地对100名年龄在 [20,45] 岁,患病后已经康复的居民做了数据统计,绘成如图所示不完整的频率分布直方图.统计员在绘制频率分布直方图的过程中所搜集的数据只能确定年龄在 [30,35) 与 [40,45] 的新冠肺炎康复人数之和是年龄在 [35,40) 的新冠肺炎康复人数的3倍,且 [30,35) 组的频率比 [40,45] 组的频率多0.15.
(1)分别求 [30,35) , [35,40) , [40,45] 组对应的频率;
(2)求年龄在 [35,45] 的新冠肺炎康复人数.
23.某种产品的质量用其质量指标值来衡量)质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为 A 配方和 B 配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A 配方的频数分布表:
指标值分组
[90,94)
[94,98)
[98,102)
[102,106)
[106,110]
频数
8
20
42
22
8
B 配方的频数分布表:
指标值分组
[90,94)
[94,98)
[98,102)
[102,106]
[106,110]
频数
4
12
42
32
10
(1)分别估计用 A 配方、 B 配方生产的产品的优质品率;
(2)已知用 B 配方生产的一件产品的利润(单位:元)与其质量指标值 t 的关系为 y={?2,t<942,94≤t<1024,t≥102 ,估计用 B 配方生产的一件产品的利润大于 0 的概率,并求用 B 配方生产的上述 100 件产品的平均利润.
答案解析部分
一、单选题
1.【答案】 C
【解析】年龄位于 [18,24) 的频率为 0.013×6=0.078 ,
年龄位于 [24,30) 的频率为 0.023×6=0.138 ,
年龄位于 [30,36) 的频率为 0.034×6=0.204 ,
年龄位于 [36,42) 的频率为 0.040×6=0.240 ,
因为 0.078+0.138+0.204=0.42<0.5 ,而
0.078+0.138+0.204+0.240=0.42=0.66>0.5 ,
所以中位数位于 [36,42) ,设中位数为 x ,
则 0.078+0.138+0.204+(x?36)×0.04=0.5 ,
解得: x=38 ,
故答案为:C.
2.【答案】 D
【解析】实线的数字为: 2,4,6,8,7,7,8,9,9,10 ,
虚线的数字为: 9,5,7,8,7,6,8,6,7,7 ,
所以 x乙=110(2+4+6+8+7+7+8+9+9+10)=7 ,
x甲=110(9+5+7+8+7+6+8+6+7+7)=7 ,
S甲2=110[(9-7)2+(5-7)2+(7?7)2+(8?7)2+?+(7?7)2]=1.2
S乙2=110[(2-7)2+(4-7)2+(6?7)2+(8?7)2+?+(10?7)2]=5.4 .
故答案为:D
3.【答案】 B
【解析】优秀人数所占的频率为 14100=0.14 ,
测试结果位于 [13,14) 的频率为 0.06<0.14 ,测试结果位于 [13,15) 的频率为 0.06+0.16<0.14 ,所以, a∈(14,15) ,
由题意可得 0.06+(a?14)×0.16=0.14 ,解得 a=14.5 。
故答案为:B.
4.【答案】 B
【解析】从全体学生中根据成绩采用分层抽样的方法抽取800名同学的试卷进行分析, 则从成绩在 [120,130) 内的学生中抽取的人数为:
800 ×[1 ?(0.005+0.010+0.010+0.015+0.025 +0.005)×10]=240。
故答案为: B
5.【答案】 D
【解析】 ∵ 该员工成绩的中位数是 93 , ∴92+90+a2=93 ,解得: a=4 .
∴x=87+89+92+97+94+996=93 ,
∴ 该员工六次业务知识考试成绩的方差: s2=16[(87?93)2+(89?93)2+ (92?93)2+(97?93)2+(94?93)2 +(99?93)2]=1066=533 .
故答案为:D.
6.【答案】 C
【解析】因为数据 axi+b,(i=1,2,?,n) 的方差是数据 xi,(i=1,2,?,n) 的方差的 a2 倍,
所以所求数据方差为 102×0.01=1
故答案为:C
7.【答案】 D
【解析】 ∵ 一个容量为1000的样本分成若干组,某组的频率为0.4,
∴ 该组的频数为: 1000×0.4=400 .
故答案为:D.
8.【答案】 C
【解析】解:对于A,观察统计图可知,A符合题意;
对于B,2019年到该地区旅游的人数是2015年的 36030=12 (倍),所以B符合题意;
对于C,2016—2019年到该地区旅游的人数平均值为 14(100+160+230+360)=212.5 (万人次),C不符合题意;
对于D,由图可知,与上一年相比,2019年到该地区旅游的人数增加得最多,D符合题意;
故答案为:C
9.【答案】 C
【解析】 xA=3+4+5+6+75=5 , xB=16+15+13+14+175=15 ,
(3?5)2+(4?5)2+(5?5)2+(6?5)2+(7?5)25=2 ,
SB2=(16?15)2+(15?15)2+(13?15)2+(14?15)2+(17?15)25=2 ,故 xA
10.【答案】 B
【解析】设贫困户总数为 a ,脱贫率 P=2×4000×9500a+2×1000×9000aa=9400 ,
所以 94007000=4735 .
故 2019 年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的 4735 倍.
故答案为:B
11.【答案】 B
【解析】 x1=7+8+8+8+95=8 , x2=6+6+7+7+105=7.2 ,故 x1>x2 .
s12=(7?8)2+(8?8)2+(8?8)2+(8?8)2+(9?8)25=0.4 ;
s22=(6?7.2)2+(6?7.2)2+(7?7.2)2+(7?7.2)2+(10?7.2)25=2.16 ,故 s12
12.【答案】 D
【解析】由图甲可知,学生总数为 4500+3500+2000=10000 (人),
故抽取的样本容量为 10000×2%=200 (人),
其中抽取的高中学生有 200×200010000=40 (人);
由图乙可知,高中生近视率为 50% ,
∴抽取的高中生近视人数为 40×50%=20 (人).
故答案为:D.
13.【答案】 C
【解析】由频率分布直方图可得,样本中底部周长小于110㎝的概率为 (0.001+0.002+0.004)×10=0.7 ,
因此在这片树木中,底部周长小于110㎝的株树大约是 10000×0.7=7000 .
故答案为:C.
14.【答案】 D
【解析】样本 1+x1,1+x2,1+x3,?,1+xn 的平均数是10,方差为2,
所以样本 2+2x1,2+2x2,2+2x3,?,2+2xn 的平均数为 2×10=20 ,方差为 22×2=8 .
故选:D.
15.【答案】 B
【解析】设池塘中草鱼的数量大约为 x ,可得 50x=750 ,
所以 x≈357 ,所以池塘中草鱼大约有 350 条.
故答案为:B.
16.【答案】 D
【解析】根据题意,x,y是方程组 {x+y=2x2+y2=10 的解,
则样本x,1,y,5中,有x+1+y+5=(x+y)+1+5=8,其平均数 x=x+1+y+54=2
其方差s2 =14× [12+x2+y2+52﹣4 ×x 2]=5,
则标准差s =5 ,
故答案为:D.
.
17.【答案】 C
【解析】由题, 1n(x1+x2+x3…+xn)=5 , 1n[(x1?5)2+(x2?5)2+...+(xn?5)2]=2 .
故 x=1n(3x1+1+3x2+1+3x3+1…+3xn+1)=1n[3(x1+x2+x3…+xn)+n]
=3×1n(x1+x2+x3…+xn)+1=3×5+1=16 .即 x=16 .
s2=1n[(3x1+1?16)2+(3x2+1?16)2+...+(3xn+1?16)2]
=1n[9(x1?5)2+9(x2?5)2+...+9(xn?5)2]
=9×1n[(x1?5)2+(x2?5)2+...+(xn?5)2]=18 .即 s2=18
故答案为:C
18.【答案】 D
【解析】设样本在 [40,60) 内的数据个数为x,
则 7+8+x50=0.6 ,
所以x=15.
故答案为:D
19.【答案】 A
【解析】由题可得: K2=100(20×20?40×20)260×40×60×40=100×400×40060×40×60×40≈2.778>2.706
故在犯错误的概率不超过10%的前提下,认为 “是否愿意外派与年龄有关”, 有90% 以上的把握认为“是否愿意外派与年龄有关,所以答案选A;
故答案为:A
20.【答案】 B
【解析】由图可知,1万元以上的项目投资占:1-0.46-0.33=0.21=21%,500×0.21=105,
少于3万元的项目投资占 821 ,则不少于3万元的项目投资占 1321
105× 1321 =65万元,
故答案为:B.
二、解答题
21.【答案】 (1)解:根据题意可知 x甲=15(8+9+12+12+14)=11 ,
x乙=15(7+9+11+13+15)=11
(2)解: s甲2=15[(8?11)2+(9?11)2+(12?11)2 +(12?11)2+(14?11)2]=4.8 ,
s乙2=15[(7?11)2+(9?11)2+(11?11)2 +(13?11)2+(15?11)2]=8 .
∵x甲=x乙 , s甲2
【解析】(1)利用平均数的定义直接求解即可;
(2)利用方差公式求出甲、乙两名运动员的方差,利用方差越小数据越稳定判断即可。
?
?
22.【答案】 (1)解:由频率分布直方图,得 [20,25) 组对应的频率为 0.01×5=0.05 , [25,30) 组对应的频率为 0.07×5=0.35 .
设 [30,35) , [35,40) , [40,45] 组对应的频率分别为 x , y , z ,则
{x+y+z=1?0.05?0.35x+z=3yx?z=0.15 ,解得 {x=0.3y=0.15z=0.15
(2)解:因为 [35,45] 对应的频率为 0.15+0.15=0.3 ,
所以年龄在 [35,45] 的新冠肺炎康复人数为 100×0.3=30
【解析】(1) 由频率分布直方图,得?[20,25)?组对应的频, 设?[30,35)? , ?[35,40)? , ?[40,45]?组对应的频率分别为?x? , ?y? , ?z? , 依题意得到方程组,解得即可;
(2)首先求出 ?[35,45] 对应的频率,即可求出康复人数。
?
?
23.【答案】 (1)解: ∵ 由试验结果知,用 A 配方生产的产品中优质品的频率为 22+8100=0.3
∴ ?用 A 配方生产的产品中优质品率的估计值为 0.3
∵ 由试验结果知,用 B 配方生产的产品中优质品的频率为 32+10100=0.42
∴ 用 B 配方生产的产品中优质品率的估计值为 0.42
(2)解:由条件知,用 B 配方生产的一件产品的利润大于 0 当且仅当其质量指标值 t≥94
由试验结果知,质量指标值 t≥94 的频率为 0.96 .
∴ 用 B 配方生产的一件产品的利润大于 0 的概率约为 0.96 .
用 B 配方生产的 100 件产品的平均利润为 1100×[4×(?2)+54×2+42×4]=2.68 (元).
【解析】(1)根据某种产品的质量用其质量指标值来衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品,根据评论计算公式即可求得答案.(2)由条件知,用 B 配方生产的一件产品的利润大于 0 当且仅当其质量指标值 t≥94 ,由试验结果知,质量指标值 t≥94 的频率为 0.96 ,用 B 配方生产的一件产品的利润大于 0 的概率约为 0.96 ,即可求得答案.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
