8.6空间直线、平面的垂直 基础练习-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析)
文档属性
| 名称 | 8.6空间直线、平面的垂直 基础练习-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 272.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-04 17:46:16 | ||
图片预览



文档简介
8.6空间直线、平面的垂直 基础练习
一、单选题
1.在棱长为 2 的正方体 ABCD?A1B1C1D1 中, O 为正方形 A1B1C1D1 的中心, P , M , N 分别为 DD1 , AB , BC 的中点,则四面体 OPMN 的体积为(??? )
A.?512??????????????????????????????????????B.?56??????????????????????????????????????C.?5212??????????????????????????????????????D.?526
2.已知两条不同的直线 l,m 和不重合的两个平面 α,β ,且 l⊥β ,有下面四个命题:①若 m⊥β ,则 l//m ;②若 α//β ,则 l⊥a ;③若 α⊥β ,则 l//α ;④若 l⊥m ,则 m//β .其中真命题的序号是(??? )
A.?①②????????????????????????????????????B.?②③????????????????????????????????????C.?②③④????????????????????????????????????D.?①④
3.三棱锥 P?ABC 的高为 PH ,若三个侧面两两垂直,则 H 一定为△ ABC 的(?? )
A.?垂心?????????????????????????????????????B.?外心?????????????????????????????????????C.?内心?????????????????????????????????????D.?重心
4.设 m , n 为两条不同的直线, α , β 为两个不同的平面,下列命题中,正确的是( ??)
A.?若 m , n 与 α 所成的角相等,则 m//n??????????????B.?若 α⊥β , m//α ,则 m⊥β
C.?若 m⊥α , m//β ,则 α⊥β???????????????????????????D.?若 m//α , n//β ,则 m//n
5.下列有关命题的说法正确的是(??? )
A.?若命题 p : ?x0∈R , ex0<1 ,则命题 ?p : ?x∈R , ex≥1
B.?“ sinx=32 ”的一个必要不充分条件是“ x=π3 ”
C.?若 |a+b|=|a|?|b| ,则 a⊥b
D.?α , β 是两个平面, m , n 是两条直线,如果 m⊥n , m⊥α , n//β ,那么 α⊥β
6.在三棱锥 P?ABC 中,已知 ∠APC=π4 , ∠BPC=π3 , PA⊥AC , PB⊥BC ,且平面 PAC⊥ 平面 PBC ,三棱锥 P?ABC 的体积为 36 ,若点 P,A,B,C 都在球O的球面上,则球O的表面积为(?? )
A.?4π???????????????????????????????????????B.?8π???????????????????????????????????????C.?12π???????????????????????????????????????D.?16π
7.如图,在以下四个正方体中,使得直线 AB 与平面 CDE 垂直的个数是(??? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
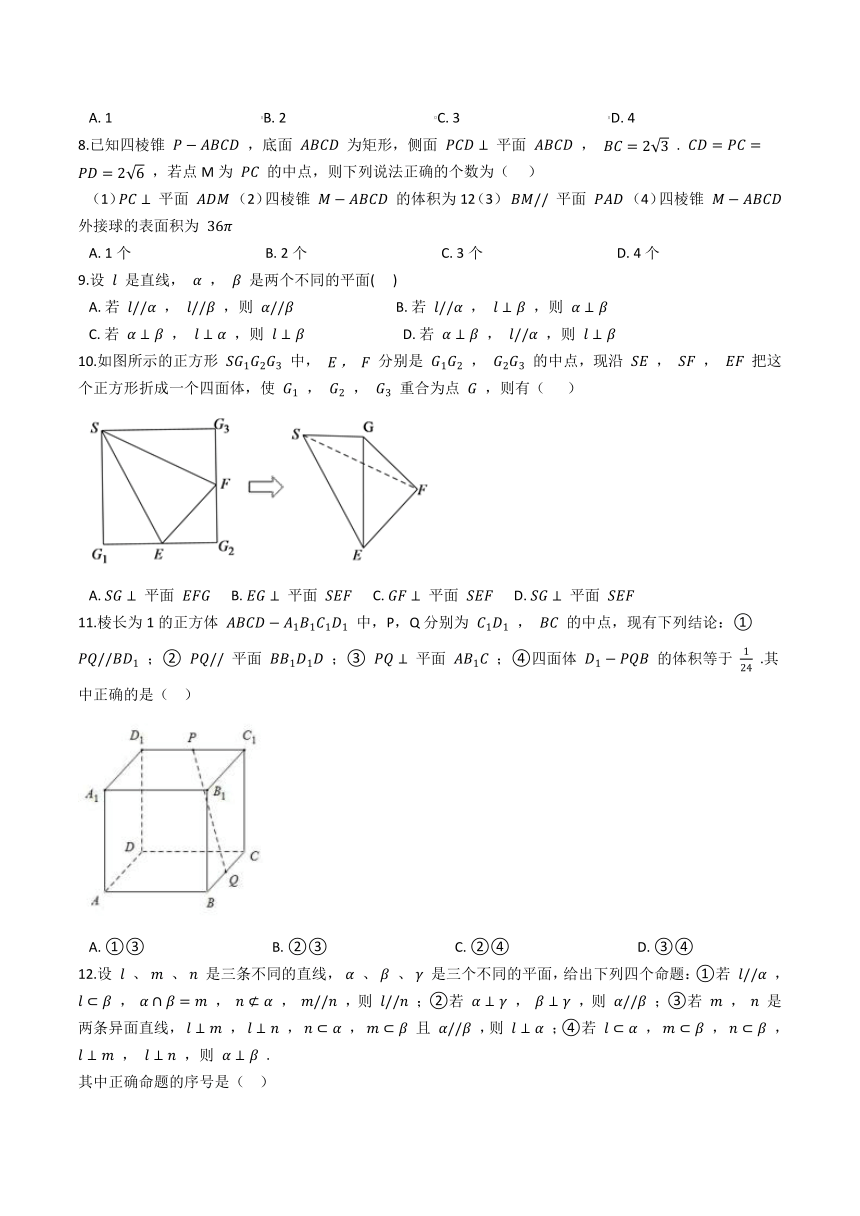
8.已知四棱锥 P?ABCD ,底面 ABCD 为矩形,侧面 PCD⊥ 平面 ABCD , BC=23 . CD=PC=PD=26 ,若点M为 PC 的中点,则下列说法正确的个数为(??? )
(1)PC⊥ 平面 ADM (2)四棱锥 M?ABCD 的体积为12(3) BM// 平面 PAD (4)四棱锥 M?ABCD 外接球的表面积为 36π
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
9.设 l 是直线, α , β 是两个不同的平面(??? )
A.?若 l//α , l//β ,则 α//β?????????????????????????????B.?若 l//α , l⊥β ,则 α⊥β
C.?若 α⊥β , l⊥α ,则 l⊥β????????????????????????????D.?若 α⊥β , l//α ,则 l⊥β
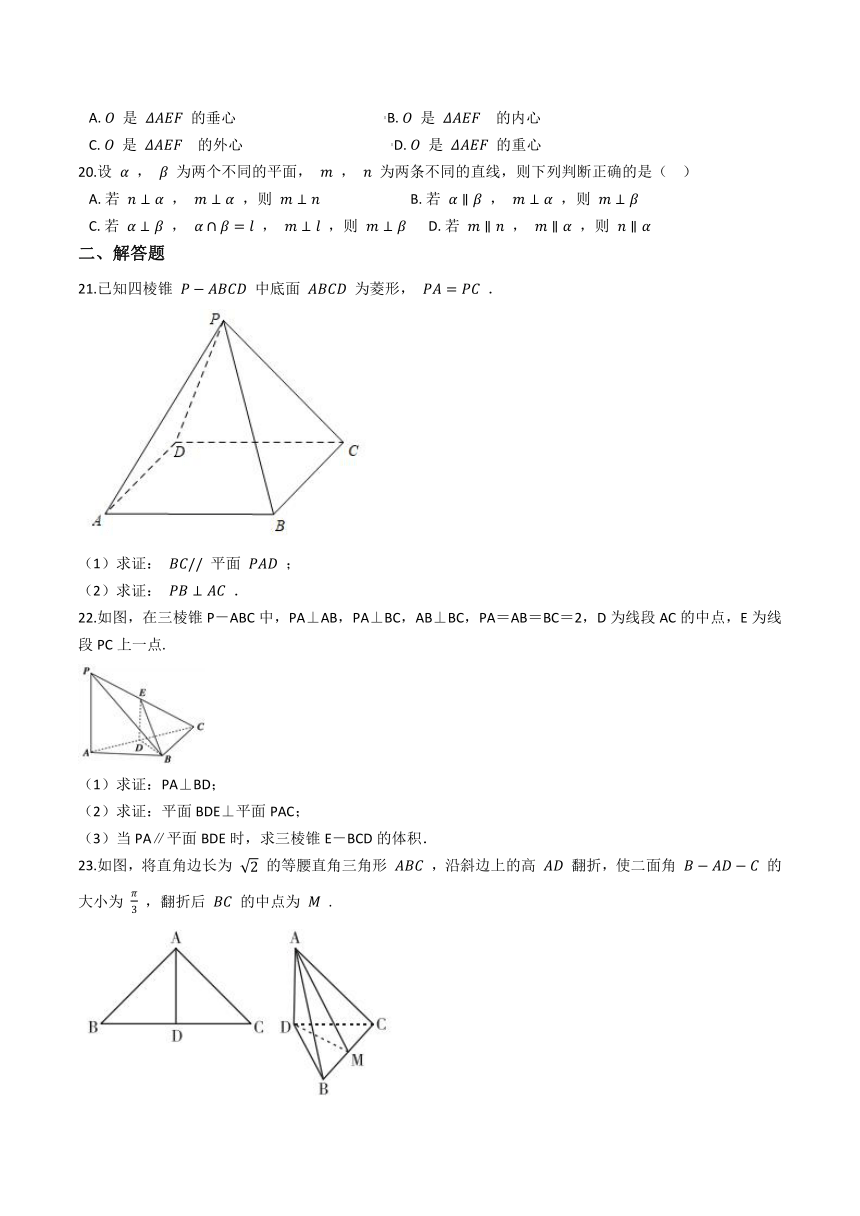
10.如图所示的正方形 SG1G2G3 中, E?,??F 分别是 G1G2 , G2G3 的中点,现沿 SE , SF , EF 把这个正方形折成一个四面体,使 G1 , G2 , G3 重合为点 G ,则有(???? )
A.?SG⊥ 平面 EFG??????B.?EG⊥ 平面 SEF??????C.?GF⊥ 平面 SEF??????D.?SG⊥ 平面 SEF
11.棱长为1的正方体 ABCD?A1B1C1D1 中,P,Q分别为 C1D1 , BC 的中点,现有下列结论:① PQ//BD1 ;② PQ// 平面 BB1D1D ;③ PQ⊥ 平面 AB1C ;④四面体 D1?PQB 的体积等于 124 .其中正确的是(?? )
A.?①③?????????????????????????????????????B.?②③?????????????????????????????????????C.?②④?????????????????????????????????????D.?③④
12.设 l 、 m 、 n 是三条不同的直线, α 、 β 、 γ 是三个不同的平面,给出下列四个命题:①若 l//α , l?β , α∩β=m , n?α , m//n ,则 l//n ;②若 α⊥γ , β⊥γ ,则 α//β ;③若 m , n 是两条异面直线, l⊥m , l⊥n , n?α , m?β 且 α//β ,则 l⊥α ;④若 l?α , m?β , n?β , l⊥m , l⊥n ,则 α⊥β .
其中正确命题的序号是(?? )
A.?①③?????????????????????????????????????B.?①④?????????????????????????????????????C.?②③?????????????????????????????????????D.?②④
13.已知a,b为两条不同的直线, α , β , γ 为三个不同的平面,则下列说法中正确的是(??? )
①若 a//α , α//β ,则 a//β ??????????????? ②若 α//β , β//γ ,则 α//γ
③若 a⊥α , b⊥α ,则 a//b ?????????????? ④若 α⊥γ , β⊥γ ,则 α⊥β
A.?①③??????????????????????????????????B.?②③??????????????????????????????????C.?①②③??????????????????????????????????D.?②③④
14.在三棱锥 P?ABC 中, PC⊥ 平面 ABC , ∠BAC=90° , AB=3 , AC=4 , ∠PBC=60° ,则三棱锥 P?ABC 外接球的体积为(?? )
A.?100π??????????????????????????????????B.?500π3??????????????????????????????????C.?125π??????????????????????????????????D.?125π3
15.已知如图,六棱锥 P?ABCDEF 的底面是正六边形, PA⊥ 平面 ABCDEF .则下列结论不正确的是(??? )
A.?CD// 平面 PAF??????????B.?DF⊥ 平面 PAF??????????C.?CF// 平面 PAB??????????D.?CF⊥ 平面 PAD
16.正方体 ABCD?A1B1C1D1 的棱长为 1 ,点 E 为棱 CC1 的中点.下列结论:①线段 BD 上存在点 F ,使得 CF// 平面 AD1E ;②线段 BD 上存在点 F ,使 CF⊥ 得平面 AD1E ;③平面 AD1E 把正方体分成两部分,较小部分的体积为 724 ,其中所有正确的序号是(??? )
A.?①??????????????????????????????????????B.?③??????????????????????????????????????C.?①③??????????????????????????????????????D.?①②③
17.已知直线 l⊥ 平面 α ,直线 m? 平面 β ,有下列四个命题:
①若 α//β ,则 l⊥m ;②若 α⊥β ,则 l//m ;③若 l//m ,则 α⊥β ;④若 l⊥m ,则 α//β .其中正确命题的序号是(??? ).
A.?①②?????????????????????????????????????B.?③④?????????????????????????????????????C.?①③?????????????????????????????????????D.?②④
18.已知长方体 ABCD?A1B1C1D1 中, AB=2BC=2AA1=2 , E , F 分别是线段 A1D1 , CC1 的中点,若 E' 是 E 在平面 BDD1B1 上的射影,点 F' 在线段 BB1 上, FF' // BC ,则 |E'F'|= (??? )
A.?21515?????????????????????????????????B.?21510?????????????????????????????????C.?43015?????????????????????????????????D.?43010
19.如图,在正方形 ABCD 中, E,F 分别是 BC,CD 的中点,沿 AE,AF,EF 把正方形折成一个四面体,
使 B,C,D 三点重合,重合后的点记为 P,P 点在△AEF 内的射影为 O ,则下列说法正确的是(??????? )
A.?O 是 ΔAEF 的垂心???????????????????????????????????????????B.?O 是 ΔAEF 的内心
C.?O 是 ΔAEF 的外心???????????????????????????????????????????D.?O 是 ΔAEF 的重心
20.设 α , β 为两个不同的平面, m , n 为两条不同的直线,则下列判断正确的是(?? )
A.?若 n⊥α , m⊥α ,则 m⊥n??????????????????????????B.?若 α∥β , m⊥α ,则 m⊥β
C.?若 α⊥β , α∩β=l , m⊥l ,则 m⊥β??????D.?若 m∥n , m∥α ,则 n∥α
二、解答题
21.已知四棱锥 P?ABCD 中底面 ABCD 为菱形, PA=PC .
(1)求证: BC// 平面 PAD ;
(2)求证: PB⊥AC .
22.如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.
(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
23.如图,将直角边长为 2 的等腰直角三角形 ABC ,沿斜边上的高 AD 翻折,使二面角 B?AD?C 的大小为 π3 ,翻折后 BC 的中点为 M .
(Ⅰ)证明 BC⊥ 平面 ADM ;
(Ⅱ)求点 D 到平面 ABC 的距离.
答案解析部分
一、单选题
1.【答案】 B
【解析】如图所示,连接 BD 交 MN 于点 Q ,连接 PQ ,连接 OD1 ,
由正方体的特点可知, MN⊥BD , MN⊥DD1 ,则根据线面垂直的判定定理可知 MN⊥ 平面 BDD1O ,则 VO?PMN=VM?OPQ+VN?OPQ=13S△OPQ?MN ,
SΔOPQ=S梯D1OQD?SΔOD1P?SΔODP=12(2+322)×2?12×1×2?12×1×322=524 ,故 VO?PMN=VM?OPQ+VN?OPQ=13S△OPQ?MN=13×524×2=56 。
故答案为:B.
2.【答案】 A
【解析】解:因为两条不同的直线 l,m 和不重合的两个平面 α,β ,且 l⊥β ,
对于①,由 l⊥β,m⊥β ,可得 l//m ,故①正确;
对于②,若 l⊥β,α//β ,可得 l⊥α ,故②正确;
对于③,若 l⊥β,α⊥β ,则有可能 l?α ,故③错误;
对于④,当 l⊥β,l⊥m 时,则有可能 m?β ,故④错误.
综上,真命题的序号是①②.
故答案为:A.
3.【答案】 A
【解析】因为三个侧面两两垂直,所以 PA⊥PB⊥PC .连结AH并延长交BC于点D.由 PA⊥PB⊥PC 知, PA⊥BC ①,由 PH 是三棱锥 P?ABC 的高得, PH⊥BC ②.由①②得, AD⊥BC .同理:连结BH并延长交AC于点E、连结CH并延长交AB于点F,则 BE⊥AC , CF⊥AB .所以,点H是三角形三边上高的交点,即H是三角形的垂心.
故答案为:A
4.【答案】 C
【解析】若 m , n 与 α 所成的角相等,则 m//n 或 m , n 相交或 m , n 异面;A不符合题意.
若 α⊥β , m//α ,则 m⊥β 或 m//β ,B不符合题意. 若 m⊥α , m//β ,则 α⊥β ,所以C正确. D.若 m//α , n//β ,则 m//n m , n 相交或 m , n 异面,D不符合题意
故答案为:C
5.【答案】 A
【解析】对于A,命题 p : ?x0∈R , ex0<1 ,则命题 ?p : ?x∈R , ex≥1 ,A符合题意;
对于B,当 x=π3 时, sinx=32 成立,
所以“ x=π3 ”是“ sinx=32 ”的充分条件,所以B不符合题意;
对于C, |a|>|b| 且两向量反向时 |a+b|=|a|?|b| 成立, a⊥b 不成立C不符合题意;
对于D,若 m⊥n , m⊥α , n//β ,则 α , β 的位置关系无法确定,D不符合题意.
故答案为:A.
6.【答案】 A
【解析】解:取 PC 中点O,连接 AO,BO ,设球半径为R,因为 ∠BPC=π3 , PA⊥AC , PB⊥BC ,
所以 AO=BO=R , PC=2R , PB=R , BC=3R ,
因为 ∠APC=π4 , PA⊥AC ,所以 PA=AC ,则 AO⊥PC ,
因为平面 PAC⊥ 平面 PBC ,所以 AO⊥ 平面 PBC ,即 VP?ABC=13S△PBC?AO=36 ,
所以 36R3=36 , ∴R=1 , ∴ 球的表面积为 4πR2=4π .
故答案为:A.
7.【答案】 B
【解析】①因为 △ABC 是正三角形,所以AB与AC的夹角为 60? ,又因为 AC//ED ,所以AB与ED的夹角为 60? ,故错误;
②因为正方形对角线相互垂直,所以 AB⊥CE , AB⊥ED,ED∩CE=E , AB⊥ 平面 CDE ,故正确;
③由①知AB与CE的夹角为 60? ,故错误;
④因为 CE⊥AD,CE⊥BD,BD∩AD=D ,所以 CE⊥ 平面 ABD ,则 AB⊥CE ,同理 AB⊥ED ,又 ED∩CE=E ,所以 AB⊥ 平面 CDE ,故正确.
故答案为:B
8.【答案】 C
【解析】作出图象,如图所示:
,
对于(1),因为侧面 PCD⊥ 平面 ABCD ,而底面 ABCD 为矩形,所以 AD⊥ 平面 PCD ,即有 AD⊥PC ,而 CD=PC=PD ,点M为 PC 的中点,所以 DM⊥PC ,故 PC⊥ 平面 ADM ,(1)正确;
对于(2),因为侧面 PCD⊥ 平面 ABCD , CD=PC=PD=26 ,所以点 P 到平面 ABCD 的距离为 26sin60?=32 ,而点M为 PC 的中点,所以点 P 到平面 ABCD 的距离为 322 ,故四棱锥 M?ABCD 的体积为 13×322×26×23=12 ,(2)正确;
对于(3),取 PD 中点 N ,连接 MN ,所以 MN//DC ,且 MN=12DC ,而 DC=AB ,
故 MN//AB ,且 MN=12AB ,因此四边形 ABMN 为梯形,所以 BM 与 AN 的延长线交于一点,故直线 BM 与平面 PAD 相交,所以(3)不正确;
对于(4),根据四棱锥 M?ABCD 的侧面 CDM 为直角三角形,底面 ABCD 为矩形,结合球的几何特征可知,四棱锥 M?ABCD 的外接球的球心在过底面 ABCD 的外心 O 且与底面垂直的直线上,同样,四棱锥 M?ABCD 的外接球的球心在过侧面 CDM 的外心( CD 的中点)且与侧面 CDM 垂直的直线上,所以四棱锥 M?ABCD 的外接球的球心即是底面 ABCD 的外心 O ,外接球半径为 OA=12(26)2+(23)2=3 ,故四棱锥 M?ABCD 外接球的表面积为 36π ,(4)正确.
故答案为:C.
9.【答案】 B
【解析】由 l 是直线, α , β 是两个不同的平面,可知:
A选项中,若 l//α , l//β ,则 α , β 可能平行也可能相交,错误;
B选项中,若 l//α , l⊥β ,由线面平行、线面垂直的性质和面面垂直的判定可知 α⊥β ,正确;
C选项中,若 α⊥β , l⊥α ,由面面垂直、线面垂直的性质可知 l//β 或 l?β ,错误;
D选项中,若 α⊥β , l//α ,则 l , β 可能平行也可能相交,错误.
故答案为:B.
10.【答案】 A
【解析】由题意: SG⊥FG , SG⊥EG ,
FG∩EG=G , FG,EG? 平面 EFG
所以 SG⊥ 平面 EFG 正确,D不正确;.
又若 EG⊥ 平面 SEF ,则 EG⊥ EF ,由平面图形可知显然不成立;
同理 GF⊥ 平面 SEF 不正确;
故答案为:A
11.【答案】 C
【解析】如图1,取 AD 中点M,连接 MD1 与 MQ ,则 MQ∥D1C1 , BD1? 平面 MQC1D1 ,则 PQ 与 BD1 异面,矛盾,故①错误;
如图2,取 CD 中点R,易得平面 PQR// 平面 BB1D1D ,故②正确;
若③正确,则 PQ⊥B1C ,则 C1Q⊥B1C ,矛盾,故③错误;
(另解:由结论 BD1⊥ 平面 AB1C 和①知 PQ , BD1 不平行也可判断错误).
V三棱锥D1?PQB=V三棱锥C1?PQB=V三棱锥P?C1QB=13×(12×12×1)×12=124 ,故④正确
(④也可以这样判断:如图3,过点B作 C1Q 的垂线,垂足为H, BH⊥C1D1 ,
因此, BH⊥ 平面 D1PQ , BH=55 , C1Q=52 ,
VD1?PQB=13S△D1PQ?BH=13×12×12×52×55=124 .
或者 VD1?PQB=VD1?C1QB=VP?C1QB=13S△C1QB?PD1=13×14×12=124 ).
故答案为:C.
12.【答案】 A
【解析】对于命题①, l//α , l?β , α∩β=m ,由直线与平面平行的性质定理可得 l//m ,
∵n?α , m//n ,由平行线的传递性可知 l//n ,命题①正确;
对于命题②, α⊥γ , β⊥γ ,则平面 α 与平面 β 平行或相交,命题②错误;
对于命题③,过直线 m 作平面 γ ,使得 γ∩α=a , ∵m?β , α//β , ∴m//α ,
∵m?γ , γ∩α=a , ∴a//m ,若 a//n ,根据平行线的传递性可得 m//n ,这与题意矛盾,
又 ∵a 、 n?α , ∴a∩n≠? , ∵l⊥m , ∴l⊥a ,又 ∵l⊥n , a 、 n?α , ∴l⊥α ,
命题③正确;
对于命题④, ∵m?β , n?β , l⊥m , l⊥n ,但 m 、 n 不一定垂直,则 l 与 β 不一定垂直,所以 α 与 β 也不一定垂直,命题④错误.
因此,正确的命题序号为①③.
故答案为:A.
13.【答案】 B
【解析】若a∥α,α∥β,得a ? β或 a//β ;所以①不正确;
若α∥β,β∥γ,则α∥γ;所以②正确;
若a⊥α,b⊥α,则a∥b;所以③正确;
若α⊥γ,β⊥γ,则α⊥β或α∥β或相交;所以④不正确;
故答案为:B
14.【答案】 B
【解析】由题意知,在三棱锥 P?ABC 中, ∠BAC=90? , AB=3 , AC=4 ,所以 BC=5 ,又由 PC⊥ 底面 ABC ,所以 PC⊥BC ,
在直角 ΔPBC 中, BC=5,∠PBC=600 ,所以 PC=10 ,
根据球的性质,可得三棱锥 P?ABC 外接球的直径为 2R=PC=10 ,即 R=5 ,
所以球的体积为 V=43πR3=43π×53=500π3 ,
故答案为:B.
15.【答案】 D
【解析】A. 因为 CD//AF,AF? 平面 PAF ,所以 CD// 平面 PAF ,故正确;
B. PA⊥ 平面 ABCDEF , DF? 平面 ABCDEF ,所以 PA⊥DF ,又 DF⊥AF,AF∩PA=A ,所以 DF⊥ 平面 PAF ,故正确;
C. 因为 CF//BA,BA? 平面 PAB ,所以 CF// 平面 PAB ,故正确;
D. 因为 CF 与 AD 成 60? 角,所以 CF 与平面 PAD 不垂直,故错误;
故答案为:D
16.【答案】 C
【解析】设 A1D 交 AD1 于 P ,过 P 作 PQ⊥AD ,交 AD 于 Q ,连接 CQ 交 BD 于 F ,由于 PQ//CE,PQ=CE ,所以四边形 PQCE 为平行四边形,所以 CQ//EP ,所以 CQ// 平面 AED1 .故线段 BD 上存在点 F ,使得 CF// 平面 AD1E ,即①正确.
若 CF⊥ 平面 AD1E , CF? 平面 ABCD ,则平面 AD1E⊥ 平面 ABCD ,这不成立,所以②错误.
延展平面 AD1E 为 AMED1 如图所示,其中 M 是 BC 的中点.根据正方体的几何性质可知, D1E,AM,DC 相交于一点, ΔCEM?ΔDD1A ,所以多面体 CEM?DD1A 是棱台.且体积为 13?(SΔCEM+SΔDD1A+SΔCEM?SΔDD1A)?CD =13?(18+12+18?12)?1=724 .故③正确.
综上所述,正确的序号为①③.
故答案为:C
17.【答案】 C
【解析】已知直线 l⊥ 平面 α ,直线 m? 平面 β ,
对于①中,若 α//β ,得到直线 l⊥ 平面 β ,所以 l⊥m ,所以是正确的;
对于②中,若 α⊥β ,直线 l 在 β 内或者 l//β ,则 l 与 m 的位置关系不确定,所以不正确;
对于③中,若 l//m ,则直线 m⊥α ,由面面垂直的性质定理,可得 α⊥β ,所以是正确;
对于④中,若 l⊥m ,则 α 与 β 可能相交,所以不正确.
故答案为:C.
18.【答案】 D
【解析】过点 E 作 EE'⊥B1D1 ,垂足为 E' ,
取 BB1 的中点 F' ,连接 FF' ,如图
则 EF'=B1E'2+B1F'2
由 AB=2BC=2AA1=2
所以 B1F'=12 , D1E=12 , B1D1=5
且 cos∠A1D1B1=A1D1B1D1=55
所以 D1E'=D1E·cos∠A1D1B1=510
故 B1E'=B1D1?D1E'=9510
所以 EF'=(9510)2+(12)2=43010 ,
故答案为:D.
19.【答案】 A
【解析】由题意得,可知 PA,PE,PF 两两垂直,由 PA⊥ 平面 PEF ,从而 PA⊥EF ,
?而 PO⊥ 平面 PEF ,从而 PO⊥EF ,
?所以 EF⊥ 平面 PAO ,
所以 EF⊥AO ,同理可知 AE⊥FO,AF⊥EO ,
所以 O 为 ΔAEF 的垂心,
故答案为:A.
20.【答案】 B
【解析】A选项不正确,根据垂直于同一个平面的两个直线平行,可得 m∥n ;B选项正确,若 α∥β ,则存在 a?α,b?α,a∩b ,在平面 β 内存在 a'∥a,b'∥b,a'∩b' ,由 m⊥α ,可得 m⊥a,m⊥b?m⊥a',m⊥b' ,由线面垂直的判定定理可得 m⊥β ;C选项不正确,因为根据面面垂直的性质定理,需要加上“ m 在平面 α 内或者平行于 α ”这个条件,才能判定 m⊥β ;D选项不正确,直线 n 可能在平面 α 上.
故答案为:B
.
二、解答题
21.【答案】 (1)证明: ∵ 四边形 ABCD 是菱形, ∴BC//AD ,
又 ∵AD? 平面 PAD , BC? 平面 PAD , ∴BC// 平面 PAD
(2)证明:连接 AC 交 BD 于 O ,连接 PO .
∵ 四边形 ABCD 为菱形, ∴AC⊥BD 且 BO=OD , OA=OC
又 PA=PC , ∴PO⊥AC
又 PO∩BD=O , ∴AC⊥ 平面 PBD ,
又 BD? 平面 PBD , ∴PB⊥AC .
【解析】(1) ∵ 四边形 ABCD 是菱形, ∴BC//AD , 再利用线线平行证出线面平行。
(2) 连接 AC 交 BD 于 O ,连接 PO ,∵ 四边形 ABCD 为菱形, ∴AC⊥BD 且 BO=OD , OA=OC , 又 PA=PC , 再利用等腰三角形三线合一,∴PO⊥AC , 再利用线线垂直证出线面垂直, ∴AC⊥ 平面 PBD , 再利用线面垂直的定义证出线线垂直。
?
22.【答案】 (1)证明:因为 PA⊥AB , PA⊥BC ,所以 PA⊥ 平面 ABC ,
又因为 BD? 平面 ABC ,所以 PA⊥BD .
(2)证明:因为 AB=BC , D 为 AC 中点,所以 BD⊥AC ,
由(I)知, PA⊥BD ,所以 BD⊥ 平面 PAC .
所以平面 BDE⊥ 平面 PAC .
(3)解:因为 PA∥ 平面 BDE ,平面 PAC∩ 平面 BDE=DE ,
所以 PA∥DE .
因为 D 为 AC 的中点,所以 DE=12PA=1 , BD=DC=2 .
由(I)知, PA⊥ 平面 ABC ,所以 DE⊥ 平面 PAC .
所以三棱锥 E?BCD 的体积 V=16BD?DC?DE=13 .
【解析】(1) 因为 PA⊥AB , PA⊥BC , 再利用线面垂直的判定定理,从而推出线面垂直,即 PA⊥ 平面 ABC , 再利用线面垂直的定义证出线线垂直,即 PA⊥BD。
(2) 因为 AB=BC , D 为 AC 中点,所以 BD⊥AC ,由(I)知, PA⊥BD ,从而由线面垂直的判定定理,从而证出线面垂直,再利用面面垂直的判定定理,从而证出面面垂直,即平面BDE⊥平面PAC。
(3)利用线面平行的性质定理证出线线平行,即 PA∥DE ,因为 D 为 AC 的中点,所以 DE=12PA=1 , BD=DC=2 ,由(I)知, PA⊥ 平面 ABC ,所以 DE⊥ 平面 PAC ,再利用三棱锥的体积公式,从而求出三棱锥E-BCD的体积。
?
23.【答案】 解:(Ⅰ)∵折叠前 AB=AC , AD 是斜边上的高,
∴ D 是 BC 的中点,∴ BD=CD ,
又因为折叠后 M 是 BC 的中点,
∴ DM⊥BC ,折叠后 AB=AC ,
∴ AM⊥BC , AM∩DM=M ,
∴ BC⊥ 平面 ADM ;
(Ⅱ)设点 D 到平面 ABC 的距离为 d ,
由题意得 VA?BCD=VD?ABC ,
∵ VA?BCD=13×34×1=312 ,
∴ VD?ABC=13×74×d=312 ,
∴ d=217 .
【解析】(Ⅰ) 由折叠的性质即可得出BD=CD , DM⊥BC由线面垂直的判定定理即可得出结论。
(1)利用等体积法代入数值计算出结果即可。
一、单选题
1.在棱长为 2 的正方体 ABCD?A1B1C1D1 中, O 为正方形 A1B1C1D1 的中心, P , M , N 分别为 DD1 , AB , BC 的中点,则四面体 OPMN 的体积为(??? )
A.?512??????????????????????????????????????B.?56??????????????????????????????????????C.?5212??????????????????????????????????????D.?526
2.已知两条不同的直线 l,m 和不重合的两个平面 α,β ,且 l⊥β ,有下面四个命题:①若 m⊥β ,则 l//m ;②若 α//β ,则 l⊥a ;③若 α⊥β ,则 l//α ;④若 l⊥m ,则 m//β .其中真命题的序号是(??? )
A.?①②????????????????????????????????????B.?②③????????????????????????????????????C.?②③④????????????????????????????????????D.?①④
3.三棱锥 P?ABC 的高为 PH ,若三个侧面两两垂直,则 H 一定为△ ABC 的(?? )
A.?垂心?????????????????????????????????????B.?外心?????????????????????????????????????C.?内心?????????????????????????????????????D.?重心
4.设 m , n 为两条不同的直线, α , β 为两个不同的平面,下列命题中,正确的是( ??)
A.?若 m , n 与 α 所成的角相等,则 m//n??????????????B.?若 α⊥β , m//α ,则 m⊥β
C.?若 m⊥α , m//β ,则 α⊥β???????????????????????????D.?若 m//α , n//β ,则 m//n
5.下列有关命题的说法正确的是(??? )
A.?若命题 p : ?x0∈R , ex0<1 ,则命题 ?p : ?x∈R , ex≥1
B.?“ sinx=32 ”的一个必要不充分条件是“ x=π3 ”
C.?若 |a+b|=|a|?|b| ,则 a⊥b
D.?α , β 是两个平面, m , n 是两条直线,如果 m⊥n , m⊥α , n//β ,那么 α⊥β
6.在三棱锥 P?ABC 中,已知 ∠APC=π4 , ∠BPC=π3 , PA⊥AC , PB⊥BC ,且平面 PAC⊥ 平面 PBC ,三棱锥 P?ABC 的体积为 36 ,若点 P,A,B,C 都在球O的球面上,则球O的表面积为(?? )
A.?4π???????????????????????????????????????B.?8π???????????????????????????????????????C.?12π???????????????????????????????????????D.?16π
7.如图,在以下四个正方体中,使得直线 AB 与平面 CDE 垂直的个数是(??? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
8.已知四棱锥 P?ABCD ,底面 ABCD 为矩形,侧面 PCD⊥ 平面 ABCD , BC=23 . CD=PC=PD=26 ,若点M为 PC 的中点,则下列说法正确的个数为(??? )
(1)PC⊥ 平面 ADM (2)四棱锥 M?ABCD 的体积为12(3) BM// 平面 PAD (4)四棱锥 M?ABCD 外接球的表面积为 36π
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
9.设 l 是直线, α , β 是两个不同的平面(??? )
A.?若 l//α , l//β ,则 α//β?????????????????????????????B.?若 l//α , l⊥β ,则 α⊥β
C.?若 α⊥β , l⊥α ,则 l⊥β????????????????????????????D.?若 α⊥β , l//α ,则 l⊥β
10.如图所示的正方形 SG1G2G3 中, E?,??F 分别是 G1G2 , G2G3 的中点,现沿 SE , SF , EF 把这个正方形折成一个四面体,使 G1 , G2 , G3 重合为点 G ,则有(???? )
A.?SG⊥ 平面 EFG??????B.?EG⊥ 平面 SEF??????C.?GF⊥ 平面 SEF??????D.?SG⊥ 平面 SEF
11.棱长为1的正方体 ABCD?A1B1C1D1 中,P,Q分别为 C1D1 , BC 的中点,现有下列结论:① PQ//BD1 ;② PQ// 平面 BB1D1D ;③ PQ⊥ 平面 AB1C ;④四面体 D1?PQB 的体积等于 124 .其中正确的是(?? )
A.?①③?????????????????????????????????????B.?②③?????????????????????????????????????C.?②④?????????????????????????????????????D.?③④
12.设 l 、 m 、 n 是三条不同的直线, α 、 β 、 γ 是三个不同的平面,给出下列四个命题:①若 l//α , l?β , α∩β=m , n?α , m//n ,则 l//n ;②若 α⊥γ , β⊥γ ,则 α//β ;③若 m , n 是两条异面直线, l⊥m , l⊥n , n?α , m?β 且 α//β ,则 l⊥α ;④若 l?α , m?β , n?β , l⊥m , l⊥n ,则 α⊥β .
其中正确命题的序号是(?? )
A.?①③?????????????????????????????????????B.?①④?????????????????????????????????????C.?②③?????????????????????????????????????D.?②④
13.已知a,b为两条不同的直线, α , β , γ 为三个不同的平面,则下列说法中正确的是(??? )
①若 a//α , α//β ,则 a//β ??????????????? ②若 α//β , β//γ ,则 α//γ
③若 a⊥α , b⊥α ,则 a//b ?????????????? ④若 α⊥γ , β⊥γ ,则 α⊥β
A.?①③??????????????????????????????????B.?②③??????????????????????????????????C.?①②③??????????????????????????????????D.?②③④
14.在三棱锥 P?ABC 中, PC⊥ 平面 ABC , ∠BAC=90° , AB=3 , AC=4 , ∠PBC=60° ,则三棱锥 P?ABC 外接球的体积为(?? )
A.?100π??????????????????????????????????B.?500π3??????????????????????????????????C.?125π??????????????????????????????????D.?125π3
15.已知如图,六棱锥 P?ABCDEF 的底面是正六边形, PA⊥ 平面 ABCDEF .则下列结论不正确的是(??? )
A.?CD// 平面 PAF??????????B.?DF⊥ 平面 PAF??????????C.?CF// 平面 PAB??????????D.?CF⊥ 平面 PAD
16.正方体 ABCD?A1B1C1D1 的棱长为 1 ,点 E 为棱 CC1 的中点.下列结论:①线段 BD 上存在点 F ,使得 CF// 平面 AD1E ;②线段 BD 上存在点 F ,使 CF⊥ 得平面 AD1E ;③平面 AD1E 把正方体分成两部分,较小部分的体积为 724 ,其中所有正确的序号是(??? )
A.?①??????????????????????????????????????B.?③??????????????????????????????????????C.?①③??????????????????????????????????????D.?①②③
17.已知直线 l⊥ 平面 α ,直线 m? 平面 β ,有下列四个命题:
①若 α//β ,则 l⊥m ;②若 α⊥β ,则 l//m ;③若 l//m ,则 α⊥β ;④若 l⊥m ,则 α//β .其中正确命题的序号是(??? ).
A.?①②?????????????????????????????????????B.?③④?????????????????????????????????????C.?①③?????????????????????????????????????D.?②④
18.已知长方体 ABCD?A1B1C1D1 中, AB=2BC=2AA1=2 , E , F 分别是线段 A1D1 , CC1 的中点,若 E' 是 E 在平面 BDD1B1 上的射影,点 F' 在线段 BB1 上, FF' // BC ,则 |E'F'|= (??? )
A.?21515?????????????????????????????????B.?21510?????????????????????????????????C.?43015?????????????????????????????????D.?43010
19.如图,在正方形 ABCD 中, E,F 分别是 BC,CD 的中点,沿 AE,AF,EF 把正方形折成一个四面体,
使 B,C,D 三点重合,重合后的点记为 P,P 点在△AEF 内的射影为 O ,则下列说法正确的是(??????? )
A.?O 是 ΔAEF 的垂心???????????????????????????????????????????B.?O 是 ΔAEF 的内心
C.?O 是 ΔAEF 的外心???????????????????????????????????????????D.?O 是 ΔAEF 的重心
20.设 α , β 为两个不同的平面, m , n 为两条不同的直线,则下列判断正确的是(?? )
A.?若 n⊥α , m⊥α ,则 m⊥n??????????????????????????B.?若 α∥β , m⊥α ,则 m⊥β
C.?若 α⊥β , α∩β=l , m⊥l ,则 m⊥β??????D.?若 m∥n , m∥α ,则 n∥α
二、解答题
21.已知四棱锥 P?ABCD 中底面 ABCD 为菱形, PA=PC .
(1)求证: BC// 平面 PAD ;
(2)求证: PB⊥AC .
22.如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.
(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
23.如图,将直角边长为 2 的等腰直角三角形 ABC ,沿斜边上的高 AD 翻折,使二面角 B?AD?C 的大小为 π3 ,翻折后 BC 的中点为 M .
(Ⅰ)证明 BC⊥ 平面 ADM ;
(Ⅱ)求点 D 到平面 ABC 的距离.
答案解析部分
一、单选题
1.【答案】 B
【解析】如图所示,连接 BD 交 MN 于点 Q ,连接 PQ ,连接 OD1 ,
由正方体的特点可知, MN⊥BD , MN⊥DD1 ,则根据线面垂直的判定定理可知 MN⊥ 平面 BDD1O ,则 VO?PMN=VM?OPQ+VN?OPQ=13S△OPQ?MN ,
SΔOPQ=S梯D1OQD?SΔOD1P?SΔODP=12(2+322)×2?12×1×2?12×1×322=524 ,故 VO?PMN=VM?OPQ+VN?OPQ=13S△OPQ?MN=13×524×2=56 。
故答案为:B.
2.【答案】 A
【解析】解:因为两条不同的直线 l,m 和不重合的两个平面 α,β ,且 l⊥β ,
对于①,由 l⊥β,m⊥β ,可得 l//m ,故①正确;
对于②,若 l⊥β,α//β ,可得 l⊥α ,故②正确;
对于③,若 l⊥β,α⊥β ,则有可能 l?α ,故③错误;
对于④,当 l⊥β,l⊥m 时,则有可能 m?β ,故④错误.
综上,真命题的序号是①②.
故答案为:A.
3.【答案】 A
【解析】因为三个侧面两两垂直,所以 PA⊥PB⊥PC .连结AH并延长交BC于点D.由 PA⊥PB⊥PC 知, PA⊥BC ①,由 PH 是三棱锥 P?ABC 的高得, PH⊥BC ②.由①②得, AD⊥BC .同理:连结BH并延长交AC于点E、连结CH并延长交AB于点F,则 BE⊥AC , CF⊥AB .所以,点H是三角形三边上高的交点,即H是三角形的垂心.
故答案为:A
4.【答案】 C
【解析】若 m , n 与 α 所成的角相等,则 m//n 或 m , n 相交或 m , n 异面;A不符合题意.
若 α⊥β , m//α ,则 m⊥β 或 m//β ,B不符合题意. 若 m⊥α , m//β ,则 α⊥β ,所以C正确. D.若 m//α , n//β ,则 m//n m , n 相交或 m , n 异面,D不符合题意
故答案为:C
5.【答案】 A
【解析】对于A,命题 p : ?x0∈R , ex0<1 ,则命题 ?p : ?x∈R , ex≥1 ,A符合题意;
对于B,当 x=π3 时, sinx=32 成立,
所以“ x=π3 ”是“ sinx=32 ”的充分条件,所以B不符合题意;
对于C, |a|>|b| 且两向量反向时 |a+b|=|a|?|b| 成立, a⊥b 不成立C不符合题意;
对于D,若 m⊥n , m⊥α , n//β ,则 α , β 的位置关系无法确定,D不符合题意.
故答案为:A.
6.【答案】 A
【解析】解:取 PC 中点O,连接 AO,BO ,设球半径为R,因为 ∠BPC=π3 , PA⊥AC , PB⊥BC ,
所以 AO=BO=R , PC=2R , PB=R , BC=3R ,
因为 ∠APC=π4 , PA⊥AC ,所以 PA=AC ,则 AO⊥PC ,
因为平面 PAC⊥ 平面 PBC ,所以 AO⊥ 平面 PBC ,即 VP?ABC=13S△PBC?AO=36 ,
所以 36R3=36 , ∴R=1 , ∴ 球的表面积为 4πR2=4π .
故答案为:A.
7.【答案】 B
【解析】①因为 △ABC 是正三角形,所以AB与AC的夹角为 60? ,又因为 AC//ED ,所以AB与ED的夹角为 60? ,故错误;
②因为正方形对角线相互垂直,所以 AB⊥CE , AB⊥ED,ED∩CE=E , AB⊥ 平面 CDE ,故正确;
③由①知AB与CE的夹角为 60? ,故错误;
④因为 CE⊥AD,CE⊥BD,BD∩AD=D ,所以 CE⊥ 平面 ABD ,则 AB⊥CE ,同理 AB⊥ED ,又 ED∩CE=E ,所以 AB⊥ 平面 CDE ,故正确.
故答案为:B
8.【答案】 C
【解析】作出图象,如图所示:
,
对于(1),因为侧面 PCD⊥ 平面 ABCD ,而底面 ABCD 为矩形,所以 AD⊥ 平面 PCD ,即有 AD⊥PC ,而 CD=PC=PD ,点M为 PC 的中点,所以 DM⊥PC ,故 PC⊥ 平面 ADM ,(1)正确;
对于(2),因为侧面 PCD⊥ 平面 ABCD , CD=PC=PD=26 ,所以点 P 到平面 ABCD 的距离为 26sin60?=32 ,而点M为 PC 的中点,所以点 P 到平面 ABCD 的距离为 322 ,故四棱锥 M?ABCD 的体积为 13×322×26×23=12 ,(2)正确;
对于(3),取 PD 中点 N ,连接 MN ,所以 MN//DC ,且 MN=12DC ,而 DC=AB ,
故 MN//AB ,且 MN=12AB ,因此四边形 ABMN 为梯形,所以 BM 与 AN 的延长线交于一点,故直线 BM 与平面 PAD 相交,所以(3)不正确;
对于(4),根据四棱锥 M?ABCD 的侧面 CDM 为直角三角形,底面 ABCD 为矩形,结合球的几何特征可知,四棱锥 M?ABCD 的外接球的球心在过底面 ABCD 的外心 O 且与底面垂直的直线上,同样,四棱锥 M?ABCD 的外接球的球心在过侧面 CDM 的外心( CD 的中点)且与侧面 CDM 垂直的直线上,所以四棱锥 M?ABCD 的外接球的球心即是底面 ABCD 的外心 O ,外接球半径为 OA=12(26)2+(23)2=3 ,故四棱锥 M?ABCD 外接球的表面积为 36π ,(4)正确.
故答案为:C.
9.【答案】 B
【解析】由 l 是直线, α , β 是两个不同的平面,可知:
A选项中,若 l//α , l//β ,则 α , β 可能平行也可能相交,错误;
B选项中,若 l//α , l⊥β ,由线面平行、线面垂直的性质和面面垂直的判定可知 α⊥β ,正确;
C选项中,若 α⊥β , l⊥α ,由面面垂直、线面垂直的性质可知 l//β 或 l?β ,错误;
D选项中,若 α⊥β , l//α ,则 l , β 可能平行也可能相交,错误.
故答案为:B.
10.【答案】 A
【解析】由题意: SG⊥FG , SG⊥EG ,
FG∩EG=G , FG,EG? 平面 EFG
所以 SG⊥ 平面 EFG 正确,D不正确;.
又若 EG⊥ 平面 SEF ,则 EG⊥ EF ,由平面图形可知显然不成立;
同理 GF⊥ 平面 SEF 不正确;
故答案为:A
11.【答案】 C
【解析】如图1,取 AD 中点M,连接 MD1 与 MQ ,则 MQ∥D1C1 , BD1? 平面 MQC1D1 ,则 PQ 与 BD1 异面,矛盾,故①错误;
如图2,取 CD 中点R,易得平面 PQR// 平面 BB1D1D ,故②正确;
若③正确,则 PQ⊥B1C ,则 C1Q⊥B1C ,矛盾,故③错误;
(另解:由结论 BD1⊥ 平面 AB1C 和①知 PQ , BD1 不平行也可判断错误).
V三棱锥D1?PQB=V三棱锥C1?PQB=V三棱锥P?C1QB=13×(12×12×1)×12=124 ,故④正确
(④也可以这样判断:如图3,过点B作 C1Q 的垂线,垂足为H, BH⊥C1D1 ,
因此, BH⊥ 平面 D1PQ , BH=55 , C1Q=52 ,
VD1?PQB=13S△D1PQ?BH=13×12×12×52×55=124 .
或者 VD1?PQB=VD1?C1QB=VP?C1QB=13S△C1QB?PD1=13×14×12=124 ).
故答案为:C.
12.【答案】 A
【解析】对于命题①, l//α , l?β , α∩β=m ,由直线与平面平行的性质定理可得 l//m ,
∵n?α , m//n ,由平行线的传递性可知 l//n ,命题①正确;
对于命题②, α⊥γ , β⊥γ ,则平面 α 与平面 β 平行或相交,命题②错误;
对于命题③,过直线 m 作平面 γ ,使得 γ∩α=a , ∵m?β , α//β , ∴m//α ,
∵m?γ , γ∩α=a , ∴a//m ,若 a//n ,根据平行线的传递性可得 m//n ,这与题意矛盾,
又 ∵a 、 n?α , ∴a∩n≠? , ∵l⊥m , ∴l⊥a ,又 ∵l⊥n , a 、 n?α , ∴l⊥α ,
命题③正确;
对于命题④, ∵m?β , n?β , l⊥m , l⊥n ,但 m 、 n 不一定垂直,则 l 与 β 不一定垂直,所以 α 与 β 也不一定垂直,命题④错误.
因此,正确的命题序号为①③.
故答案为:A.
13.【答案】 B
【解析】若a∥α,α∥β,得a ? β或 a//β ;所以①不正确;
若α∥β,β∥γ,则α∥γ;所以②正确;
若a⊥α,b⊥α,则a∥b;所以③正确;
若α⊥γ,β⊥γ,则α⊥β或α∥β或相交;所以④不正确;
故答案为:B
14.【答案】 B
【解析】由题意知,在三棱锥 P?ABC 中, ∠BAC=90? , AB=3 , AC=4 ,所以 BC=5 ,又由 PC⊥ 底面 ABC ,所以 PC⊥BC ,
在直角 ΔPBC 中, BC=5,∠PBC=600 ,所以 PC=10 ,
根据球的性质,可得三棱锥 P?ABC 外接球的直径为 2R=PC=10 ,即 R=5 ,
所以球的体积为 V=43πR3=43π×53=500π3 ,
故答案为:B.
15.【答案】 D
【解析】A. 因为 CD//AF,AF? 平面 PAF ,所以 CD// 平面 PAF ,故正确;
B. PA⊥ 平面 ABCDEF , DF? 平面 ABCDEF ,所以 PA⊥DF ,又 DF⊥AF,AF∩PA=A ,所以 DF⊥ 平面 PAF ,故正确;
C. 因为 CF//BA,BA? 平面 PAB ,所以 CF// 平面 PAB ,故正确;
D. 因为 CF 与 AD 成 60? 角,所以 CF 与平面 PAD 不垂直,故错误;
故答案为:D
16.【答案】 C
【解析】设 A1D 交 AD1 于 P ,过 P 作 PQ⊥AD ,交 AD 于 Q ,连接 CQ 交 BD 于 F ,由于 PQ//CE,PQ=CE ,所以四边形 PQCE 为平行四边形,所以 CQ//EP ,所以 CQ// 平面 AED1 .故线段 BD 上存在点 F ,使得 CF// 平面 AD1E ,即①正确.
若 CF⊥ 平面 AD1E , CF? 平面 ABCD ,则平面 AD1E⊥ 平面 ABCD ,这不成立,所以②错误.
延展平面 AD1E 为 AMED1 如图所示,其中 M 是 BC 的中点.根据正方体的几何性质可知, D1E,AM,DC 相交于一点, ΔCEM?ΔDD1A ,所以多面体 CEM?DD1A 是棱台.且体积为 13?(SΔCEM+SΔDD1A+SΔCEM?SΔDD1A)?CD =13?(18+12+18?12)?1=724 .故③正确.
综上所述,正确的序号为①③.
故答案为:C
17.【答案】 C
【解析】已知直线 l⊥ 平面 α ,直线 m? 平面 β ,
对于①中,若 α//β ,得到直线 l⊥ 平面 β ,所以 l⊥m ,所以是正确的;
对于②中,若 α⊥β ,直线 l 在 β 内或者 l//β ,则 l 与 m 的位置关系不确定,所以不正确;
对于③中,若 l//m ,则直线 m⊥α ,由面面垂直的性质定理,可得 α⊥β ,所以是正确;
对于④中,若 l⊥m ,则 α 与 β 可能相交,所以不正确.
故答案为:C.
18.【答案】 D
【解析】过点 E 作 EE'⊥B1D1 ,垂足为 E' ,
取 BB1 的中点 F' ,连接 FF' ,如图
则 EF'=B1E'2+B1F'2
由 AB=2BC=2AA1=2
所以 B1F'=12 , D1E=12 , B1D1=5
且 cos∠A1D1B1=A1D1B1D1=55
所以 D1E'=D1E·cos∠A1D1B1=510
故 B1E'=B1D1?D1E'=9510
所以 EF'=(9510)2+(12)2=43010 ,
故答案为:D.
19.【答案】 A
【解析】由题意得,可知 PA,PE,PF 两两垂直,由 PA⊥ 平面 PEF ,从而 PA⊥EF ,
?而 PO⊥ 平面 PEF ,从而 PO⊥EF ,
?所以 EF⊥ 平面 PAO ,
所以 EF⊥AO ,同理可知 AE⊥FO,AF⊥EO ,
所以 O 为 ΔAEF 的垂心,
故答案为:A.
20.【答案】 B
【解析】A选项不正确,根据垂直于同一个平面的两个直线平行,可得 m∥n ;B选项正确,若 α∥β ,则存在 a?α,b?α,a∩b ,在平面 β 内存在 a'∥a,b'∥b,a'∩b' ,由 m⊥α ,可得 m⊥a,m⊥b?m⊥a',m⊥b' ,由线面垂直的判定定理可得 m⊥β ;C选项不正确,因为根据面面垂直的性质定理,需要加上“ m 在平面 α 内或者平行于 α ”这个条件,才能判定 m⊥β ;D选项不正确,直线 n 可能在平面 α 上.
故答案为:B
.
二、解答题
21.【答案】 (1)证明: ∵ 四边形 ABCD 是菱形, ∴BC//AD ,
又 ∵AD? 平面 PAD , BC? 平面 PAD , ∴BC// 平面 PAD
(2)证明:连接 AC 交 BD 于 O ,连接 PO .
∵ 四边形 ABCD 为菱形, ∴AC⊥BD 且 BO=OD , OA=OC
又 PA=PC , ∴PO⊥AC
又 PO∩BD=O , ∴AC⊥ 平面 PBD ,
又 BD? 平面 PBD , ∴PB⊥AC .
【解析】(1) ∵ 四边形 ABCD 是菱形, ∴BC//AD , 再利用线线平行证出线面平行。
(2) 连接 AC 交 BD 于 O ,连接 PO ,∵ 四边形 ABCD 为菱形, ∴AC⊥BD 且 BO=OD , OA=OC , 又 PA=PC , 再利用等腰三角形三线合一,∴PO⊥AC , 再利用线线垂直证出线面垂直, ∴AC⊥ 平面 PBD , 再利用线面垂直的定义证出线线垂直。
?
22.【答案】 (1)证明:因为 PA⊥AB , PA⊥BC ,所以 PA⊥ 平面 ABC ,
又因为 BD? 平面 ABC ,所以 PA⊥BD .
(2)证明:因为 AB=BC , D 为 AC 中点,所以 BD⊥AC ,
由(I)知, PA⊥BD ,所以 BD⊥ 平面 PAC .
所以平面 BDE⊥ 平面 PAC .
(3)解:因为 PA∥ 平面 BDE ,平面 PAC∩ 平面 BDE=DE ,
所以 PA∥DE .
因为 D 为 AC 的中点,所以 DE=12PA=1 , BD=DC=2 .
由(I)知, PA⊥ 平面 ABC ,所以 DE⊥ 平面 PAC .
所以三棱锥 E?BCD 的体积 V=16BD?DC?DE=13 .
【解析】(1) 因为 PA⊥AB , PA⊥BC , 再利用线面垂直的判定定理,从而推出线面垂直,即 PA⊥ 平面 ABC , 再利用线面垂直的定义证出线线垂直,即 PA⊥BD。
(2) 因为 AB=BC , D 为 AC 中点,所以 BD⊥AC ,由(I)知, PA⊥BD ,从而由线面垂直的判定定理,从而证出线面垂直,再利用面面垂直的判定定理,从而证出面面垂直,即平面BDE⊥平面PAC。
(3)利用线面平行的性质定理证出线线平行,即 PA∥DE ,因为 D 为 AC 的中点,所以 DE=12PA=1 , BD=DC=2 ,由(I)知, PA⊥ 平面 ABC ,所以 DE⊥ 平面 PAC ,再利用三棱锥的体积公式,从而求出三棱锥E-BCD的体积。
?
23.【答案】 解:(Ⅰ)∵折叠前 AB=AC , AD 是斜边上的高,
∴ D 是 BC 的中点,∴ BD=CD ,
又因为折叠后 M 是 BC 的中点,
∴ DM⊥BC ,折叠后 AB=AC ,
∴ AM⊥BC , AM∩DM=M ,
∴ BC⊥ 平面 ADM ;
(Ⅱ)设点 D 到平面 ABC 的距离为 d ,
由题意得 VA?BCD=VD?ABC ,
∵ VA?BCD=13×34×1=312 ,
∴ VD?ABC=13×74×d=312 ,
∴ d=217 .
【解析】(Ⅰ) 由折叠的性质即可得出BD=CD , DM⊥BC由线面垂直的判定定理即可得出结论。
(1)利用等体积法代入数值计算出结果即可。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
