10.3频率与概率 基础练习-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析)
文档属性
| 名称 | 10.3频率与概率 基础练习-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 130.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-04 17:47:07 | ||
图片预览


文档简介
10.3频率与概率 基础练习
一、单选题
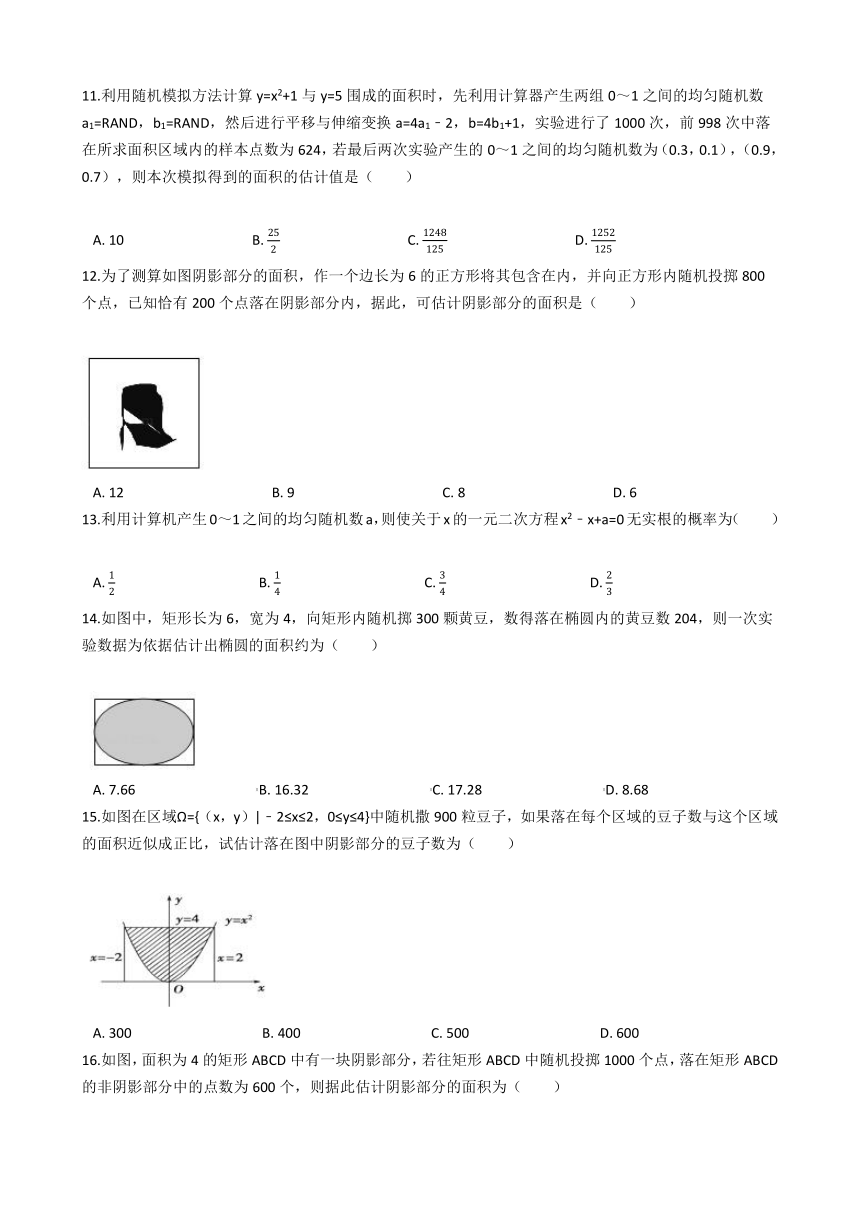
1.《九章算术》中有如下问题:“今有勾八步,股一十五步,问勾中容圆,径几何?”其大意:“已知直角三角形两直角边长分别为8步和15步,问其内切圆的直径为多少步?”现若向此三角形内随机投一粒豆子,则豆子落在其内切圆外的概率是(?? )
A.?3π10???????????????????????????????????B.?3π20???????????????????????????????????C.?1?3π10???????????????????????????????????D.?1?3π20
2.如图,“赵爽弦图”是由四个全等的直角三角形(阴影部分)围成一个大正方形,中间空出一个小正方形组成的图形,若在大正方形内随机取一点,该点落在小正方形的概率为 15 ,则图中直角三角形中较大锐角的正弦值为(?? )
A.?55???????????????????????????????????????B.?255???????????????????????????????????????C.?15???????????????????????????????????????D.?33
3.下面四个残差图中可以反映出回归模型拟合精度较好的为(?? )
A.?图1???????????????????????????????????????B.?图2???????????????????????????????????????C.?图3???????????????????????????????????????D.?图4
4.现用随机模拟方法近似计算积分 ∫02 1?x24 dx,先产生两组(每组1000个)在区间[0,2]上的均匀随机数x1 , x2 , x3 , …,x1000和y1 , y2 , y3 , …,y1000 , 由此得到1000个点(xi , yi)(i=1,2,…,1000),再数出其中满足 xi24 + yi2 ≤1(i=1,2,…,1000)的点数400,那么由随机模拟方法可得积分 ∫02 1?x24 dx的近似值为(?? )
A.?1.4???????????????????????????????????????B.?1.6???????????????????????????????????????C.?1.8???????????????????????????????????????D.?2.0
5.为了测算如图阴影部分的面积,作一个边长为6的正方形将其包含在内,并向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是(?? )
A.?12???????????????????????????????????????????B.?9???????????????????????????????????????????C.?8???????????????????????????????????????????D.?6
6.甲乙两位同学进行乒乓球比赛,甲获胜的概率为0.4,现采用随机模拟的方法估计这两位同学打3局比赛甲恰好获胜2局的概率:先利用计算器产生0到9之间取整数值的随机数,制定1,2,3,4表示甲获胜,用5,6,7,8,9,0表示乙获胜,再以每三个随机数为一组,代表3局比赛的结果,经随机模拟产生了30组随机数
102?? 231?? 146?? 027?? 590?? 763?? 245?? 207?? 310?? 386?? 350?? 481?? 337?? 286?? 139
579?? 684?? 487?? 370?? 175?? 772?? 235?? 246?? 487?? 569?? 047?? 008?? 341?? 287?? 114
据此估计,这两位同学打3局比赛甲恰好获胜2局的概率为(?? )
A.?13????????????????????????????????????????B.?310????????????????????????????????????????C.?25????????????????????????????????????????D.?1130
7.如图,已知正方形的面积为100,向正方形内随机地撒200颗黄豆,数得落在阴影外的黄豆数为114颗,以此实验数据为依据,可以估计出阴影部分的面积约为(?? )
A.?53?????????????????????????????????????????B.?43?????????????????????????????????????????C.?47?????????????????????????????????????????D.?57
8.在利用随机模拟方法估计函数y=x2的图象、直线x=﹣1,x=1以及x轴所围成的图形面积时,做了1000次试验,数出落在该区域中的样本点数为302个,则该区域面积的近似值为(? )
A.?0.604??????????????????????????????????B.?0.698??????????????????????????????????C.?0.151??????????????????????????????????D.?0.302
9.已知某运动员每次投篮命中的概率低于40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为(?? )
A.?0.35?????????????????????????????????????B.?0.25?????????????????????????????????????C.?0.20?????????????????????????????????????D.?0.15
10.利用计算机在区间(0,1)上产生两个随机数a和b,则方程x=-2a-b2x有实根的概率为( )
A.?16??????????????????????????????????????????B.?23??????????????????????????????????????????C.?12??????????????????????????????????????????D.?13
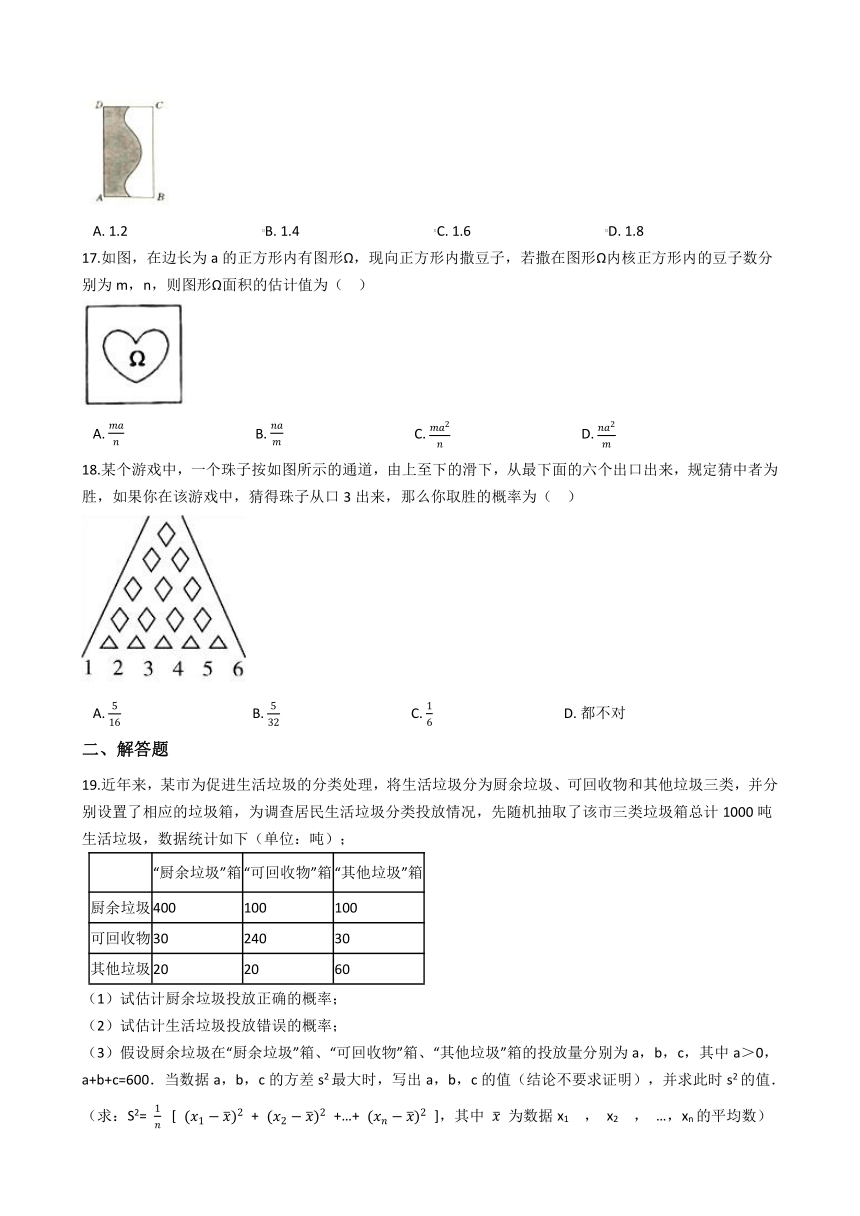
11.利用随机模拟方法计算y=x2+1与y=5围成的面积时,先利用计算器产生两组0~1之间的均匀随机数a1=RAND,b1=RAND,然后进行平移与伸缩变换a=4a1﹣2,b=4b1+1,实验进行了1000次,前998次中落在所求面积区域内的样本点数为624,若最后两次实验产生的0~1之间的均匀随机数为(0.3,0.1),(0.9,0.7),则本次模拟得到的面积的估计值是( )
A.?10?????????????????????????????????????B.?252?????????????????????????????????????C.?1248125?????????????????????????????????????D.?1252125
12.为了测算如图阴影部分的面积,作一个边长为6的正方形将其包含在内,并向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是( )
A.?12???????????????????????????????????????????B.?9???????????????????????????????????????????C.?8???????????????????????????????????????????D.?6
13.利用计算机产生0~1之间的均匀随机数a,则使关于x的一元二次方程x2﹣x+a=0无实根的概率为( )
A.?12??????????????????????????????????????????B.?14??????????????????????????????????????????C.?34??????????????????????????????????????????D.?23
14.如图中,矩形长为6,宽为4,向矩形内随机掷300颗黄豆,数得落在椭圆内的黄豆数204,则一次实验数据为依据估计出椭圆的面积约为( )
A.?7.66???????????????????????????????????B.?16.32???????????????????????????????????C.?17.28???????????????????????????????????D.?8.68
15.如图在区域Ω={(x,y)|﹣2≤x≤2,0≤y≤4}中随机撒900粒豆子,如果落在每个区域的豆子数与这个区域的面积近似成正比,试估计落在图中阴影部分的豆子数为( )
A.?300??????????????????????????????????????B.?400??????????????????????????????????????C.?500??????????????????????????????????????D.?600
16.如图,面积为4的矩形ABCD中有一块阴影部分,若往矩形ABCD中随机投掷1000个点,落在矩形ABCD的非阴影部分中的点数为600个,则据此估计阴影部分的面积为( )
A.?1.2???????????????????????????????????????B.?1.4???????????????????????????????????????C.?1.6???????????????????????????????????????D.?1.8
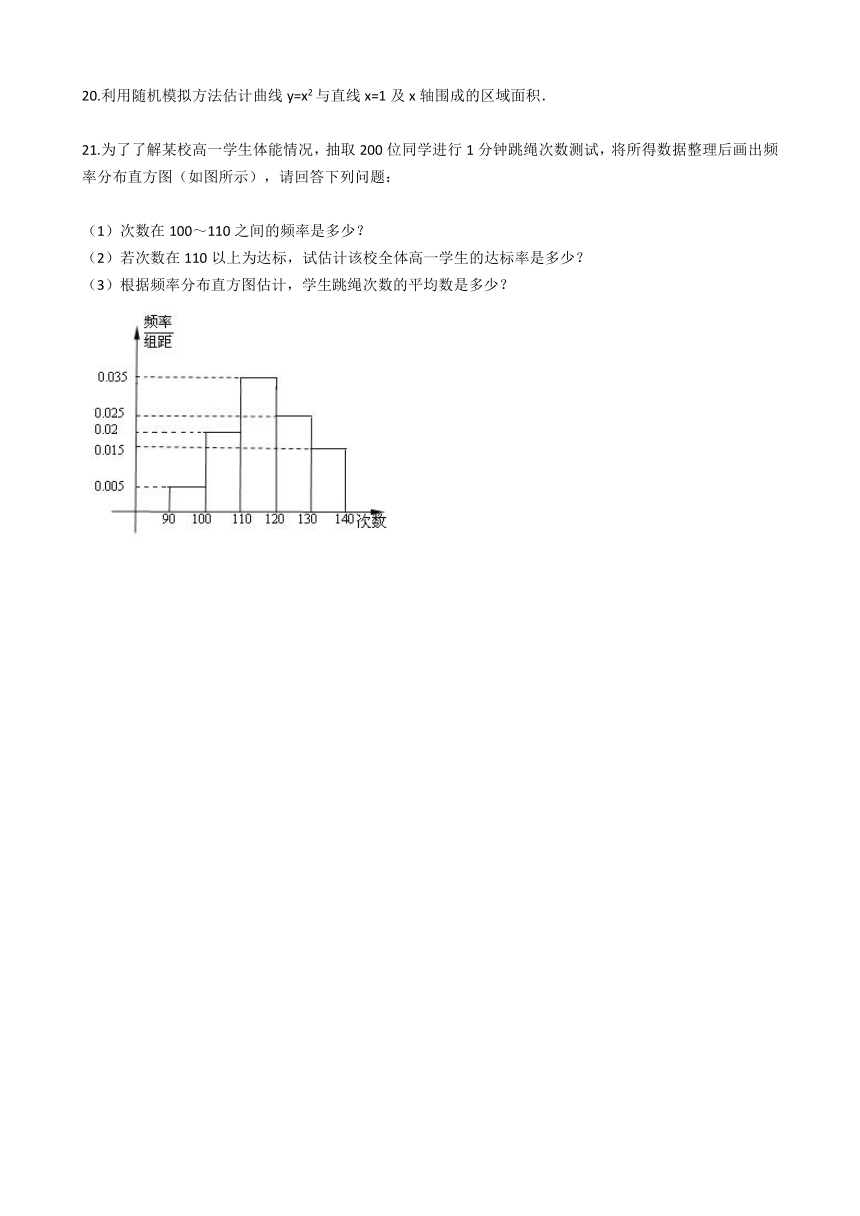
17.如图,在边长为a的正方形内有图形Ω,现向正方形内撒豆子,若撒在图形Ω内核正方形内的豆子数分别为m,n,则图形Ω面积的估计值为(?? )
A.?man??????????????????????????????????????B.?nam??????????????????????????????????????C.?ma2n??????????????????????????????????????D.?na2m
18.某个游戏中,一个珠子按如图所示的通道,由上至下的滑下,从最下面的六个出口出来,规定猜中者为胜,如果你在该游戏中,猜得珠子从口3出来,那么你取胜的概率为(?? )
A.?516??????????????????????????????????????B.?532??????????????????????????????????????C.?16??????????????????????????????????????D.?都不对
二、解答题
19.近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,先随机抽取了该市三类垃圾箱总计1000吨生活垃圾,数据统计如下(单位:吨);
“厨余垃圾”箱
“可回收物”箱
“其他垃圾”箱
厨余垃圾
400
100
100
可回收物
30
240
30
其他垃圾
20
20
60
(1)试估计厨余垃圾投放正确的概率;
(2)试估计生活垃圾投放错误的概率;
(3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c的方差s2最大时,写出a,b,c的值(结论不要求证明),并求此时s2的值.
(求:S2= 1n ?[ (x1?x)2 + (x2?x)2 +…+ (xn?x)2 ],其中 x 为数据x1 , x2 , …,xn的平均数)
20.利用随机模拟方法估计曲线y=x2与直线x=1及x轴围成的区域面积.
21.为了了解某校高一学生体能情况,抽取200位同学进行1分钟跳绳次数测试,将所得数据整理后画出频率分布直方图(如图所示),请回答下列问题:
(1)次数在100~110之间的频率是多少?
(2)若次数在110以上为达标,试估计该校全体高一学生的达标率是多少?
(3)根据频率分布直方图估计,学生跳绳次数的平均数是多少?
答案解析部分
一、单选题
1.【答案】D
【解析】解:直角三角形的斜边长为 82+152 =17,
设内切圆的半径为r,则8﹣r+15﹣r=17,解得r=3.
∴内切圆的面积为πr2=9π,
∴豆子落在内切圆外部的概率P=1﹣ 9π12×8×15 =1﹣ 3π20 .
故答案为:D.
2.【答案】B
【解析】解:在大正方形内随机取一点,这一点落在小正方形的概率为 15 , 不妨设大正方形面积为5,小正方形面积为1,
∴大正方形边长为 5 ,小正方形的边长为1.
∴四个全等的直角三角形的斜边的长是 5 ,
较短的直角边的长是1,较长的直角边的长是2,
故sinθ= 25=255 ,
故选:B.
3.【答案】A
【解析】解:据残差图显示的分布情况即可看出图1显示的残差分布集中,拟合度较好, 故选A.
4.【答案】B
【解析】解:由题意,由随机模拟方法可得积分 ∫02 1?x24 dx的近似值为 4001000×4 =1.6, 故选B.
5.【答案】 B
【解析】解:根据题意,设阴影部分的面积为S,则正方形的面积为36,
向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,
则向正方形内随机投掷一点,其落到阴影部分的概率P= 200800 = 14 ;
而P= s36 ,则 s36 = 14 ,
解可得,S=9;
故选B.
6.【答案】 B
【解析】解:由题意知模拟打3局比赛甲恰好获胜2局的结果,经随机模拟产生了如下20组随机数,
在30组随机数中表示打3局比赛甲恰好获胜2局的有:102,146,245,310,481,337,139,235,246,共9组随机数,
∴所求概率为 930 = 310 .
故答案为:B.
7.【答案】 B
【解析】解:设阴影外部分的面积为s,
则由几何概型的概率公式得: ,
解得s=57,
可以估计出阴影部分的面积约为100﹣57=43.
故选:B.
8.【答案】 A
【解析】解:设区域面积为x,
由概率的几何概型知,则 3021000=x2 ,
解得x=0.604.
则该区域面积的近似值为0.604,
故选:A.
9.【答案】 B
【解析】解:由题意知模拟三次投篮的结果,经随机模拟产生了如下20组随机数,
在20组随机数中表示三次投篮恰有两次命中的有:191、271、932、812、393.
共5组随机数,
∴所求概率为 520=14 =0.25.
故选B.
10.【答案】 C
【解析】解:由题意知本题是一个几何概型,x=-2a-b2x
化为x2+2ax+b2=0,方程有实根,△≥0
即4a2﹣4b2≥0
∴b≤a.
在aOb坐标系中画出图形.如图.∴方程有实根的概率为P=
故选C.
11.【答案】 A
【解析】解:由a1=0.3,b1=0.1得a=﹣0.8,b=1.4,(﹣0.8,1.4)落在y=x2+1与y=5围成的区域内,
由a1=0.9,b1=0.7得:a=1.6,b=3.8,(1.6,3.8)落在y=x2+1与y=5围成的区域外,
所以本次模拟得出的面积为 16×6251000=10.
故选:A
12.【答案】 B
【解析】解:根据题意,设阴影部分的面积为S,则正方形的面积为36,
向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,
则向正方形内随机投掷一点,其落到阴影部分的概率P= 200800=14;
?,
解可得,S=9;
故选B.
.
13.【答案】 C
【解析】解:∵关于x的一元二次方程x2﹣x+a=0无实根,
∴△=1﹣4a<0,
∵0<a<1,
∴14∴事件“关于x的一元二次方程x2﹣x+a=0无实根”的概率为P=1?141=34.
故选:C.
14.【答案】 B
【解析】解:黄豆落在椭圆外的概率为: 204300=24?S24
解得:S=16.32.
故选:B.
15.【答案】 D
【解析】解:区域Ω的面积为S1=16.
图中阴影部分的面积:S2=S1﹣2.
设落在阴影部分的豆子数为m,由已知条件, 即m=600.
因此落在图中阴影部分的豆子约为600粒.
16.【答案】 C
【解析】解:根据几何概率的计算公式可得,向距形内随机投掷1000个点,落在矩形ABCD的非阴影部分中的点数为600个,则落在矩形ABCD的阴影部分中的点数为400个,
设阴影部分的面积为S,落在阴影部分为事件A,
∴落在阴影部分的概率P(A)= , 解得S=1.6.
故选C.
17.【答案】 C
【解析】解:如图,在边长为a的正方形内有图形Ω,则正方形的面积为a2 ,
现向正方形内撒豆子,
若撒在图形Ω内和正方形内的豆子数分别为m,n,
则图形Ω面积的估计值为: mn×a2 = ma2n .
故答案为:C.
18.【答案】 A
【解析】所求的概率为 P=C5225=516 ?,故选A.
二、解答题
19.【答案】 (1)解:由题意可知:厨余垃圾600吨,投放到“厨余垃圾”箱400吨,故厨余垃圾投放正确的概率为 400600=23
(2)解:由题意可知:生活垃圾投放错误有200+60+20+20=300,故生活垃圾投放错误的概率为 3001000=310
(3)解:由题意可知:∵a+b+c=600,∴a,b,c的平均数为200
∴ s2=13[(a?200)2+(b?200)2+(c?200)2] = 13(a2+b2+c2?120000) ,
∵(a+b+c)2=a2+b2+c2+2ab+2bc+2ac≥a2+b2+c2 , 因此有当a=600,b=0,c=0时,有s2=80000
【解析】(1)厨余垃圾600吨,投放到“厨余垃圾”箱400吨,故可求厨余垃圾投放正确的概率;(2)生活垃圾投放错误有200+60+20+20=300,故可求生活垃圾投放错误的概率;(3)计算方差可得 s2=13[(a?200)2+(b?200)2+(c?200)2] = 13(a2+b2+c2?120000) ,因此有当a=600,b=0,c=0时,有s2=80000.
20.【答案】 解:(1)利用计算机分别产生[0,1]和[0,1]上的均匀随机数:a=Rand和b=Rand,得随机数组(a,b).
(2)统计试验总次数N和落在“曲边梯形”内的点数N1(满足b<a2的点(a,b)数)
(3)计算频率 N1N , 得点落在“曲边梯形”上的概率近似值.
(4)由几何概型得p=S1 , 所以N1N=S1 , 于是得到S=N1N , 这就是“曲边梯形”面积的近似值.
【解析】先由计算器做模拟试验结果试验估计,满足条件b<a2的点(a,b)的概率,再转化为几何概型的面积类型求解.
21.【答案】 (1)∵第二组面积为0.02×10=0.2,
∴次数在100~110之间的频率是0.2.
∵第二小组频数为12;
(2)∵次数在110以上(含110次)为达标,
∴高一学生的达标率是 10×(0.035+0.025+0.015)=75%
即高一有75%的学生达标.
(3)根据频率分布直方图估计,学生跳绳次数的平均数是95×0.05+105×0.2+115×0.35+125×0.25+135×0.15=117.5.
【解析】(1)根据第二组小矩形的面积,做出第二组的频率.
(2)从频率分步直方图中看出次数子啊110以上的频数,用频数除以样本容量得到达标率,进而估计高一全体学生的达标率.
(3)将每组的组中值乘以该组的频率即可求出学生跳绳次数的平均数.
一、单选题
1.《九章算术》中有如下问题:“今有勾八步,股一十五步,问勾中容圆,径几何?”其大意:“已知直角三角形两直角边长分别为8步和15步,问其内切圆的直径为多少步?”现若向此三角形内随机投一粒豆子,则豆子落在其内切圆外的概率是(?? )
A.?3π10???????????????????????????????????B.?3π20???????????????????????????????????C.?1?3π10???????????????????????????????????D.?1?3π20
2.如图,“赵爽弦图”是由四个全等的直角三角形(阴影部分)围成一个大正方形,中间空出一个小正方形组成的图形,若在大正方形内随机取一点,该点落在小正方形的概率为 15 ,则图中直角三角形中较大锐角的正弦值为(?? )
A.?55???????????????????????????????????????B.?255???????????????????????????????????????C.?15???????????????????????????????????????D.?33
3.下面四个残差图中可以反映出回归模型拟合精度较好的为(?? )
A.?图1???????????????????????????????????????B.?图2???????????????????????????????????????C.?图3???????????????????????????????????????D.?图4
4.现用随机模拟方法近似计算积分 ∫02 1?x24 dx,先产生两组(每组1000个)在区间[0,2]上的均匀随机数x1 , x2 , x3 , …,x1000和y1 , y2 , y3 , …,y1000 , 由此得到1000个点(xi , yi)(i=1,2,…,1000),再数出其中满足 xi24 + yi2 ≤1(i=1,2,…,1000)的点数400,那么由随机模拟方法可得积分 ∫02 1?x24 dx的近似值为(?? )
A.?1.4???????????????????????????????????????B.?1.6???????????????????????????????????????C.?1.8???????????????????????????????????????D.?2.0
5.为了测算如图阴影部分的面积,作一个边长为6的正方形将其包含在内,并向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是(?? )
A.?12???????????????????????????????????????????B.?9???????????????????????????????????????????C.?8???????????????????????????????????????????D.?6
6.甲乙两位同学进行乒乓球比赛,甲获胜的概率为0.4,现采用随机模拟的方法估计这两位同学打3局比赛甲恰好获胜2局的概率:先利用计算器产生0到9之间取整数值的随机数,制定1,2,3,4表示甲获胜,用5,6,7,8,9,0表示乙获胜,再以每三个随机数为一组,代表3局比赛的结果,经随机模拟产生了30组随机数
102?? 231?? 146?? 027?? 590?? 763?? 245?? 207?? 310?? 386?? 350?? 481?? 337?? 286?? 139
579?? 684?? 487?? 370?? 175?? 772?? 235?? 246?? 487?? 569?? 047?? 008?? 341?? 287?? 114
据此估计,这两位同学打3局比赛甲恰好获胜2局的概率为(?? )
A.?13????????????????????????????????????????B.?310????????????????????????????????????????C.?25????????????????????????????????????????D.?1130
7.如图,已知正方形的面积为100,向正方形内随机地撒200颗黄豆,数得落在阴影外的黄豆数为114颗,以此实验数据为依据,可以估计出阴影部分的面积约为(?? )
A.?53?????????????????????????????????????????B.?43?????????????????????????????????????????C.?47?????????????????????????????????????????D.?57
8.在利用随机模拟方法估计函数y=x2的图象、直线x=﹣1,x=1以及x轴所围成的图形面积时,做了1000次试验,数出落在该区域中的样本点数为302个,则该区域面积的近似值为(? )
A.?0.604??????????????????????????????????B.?0.698??????????????????????????????????C.?0.151??????????????????????????????????D.?0.302
9.已知某运动员每次投篮命中的概率低于40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为(?? )
A.?0.35?????????????????????????????????????B.?0.25?????????????????????????????????????C.?0.20?????????????????????????????????????D.?0.15
10.利用计算机在区间(0,1)上产生两个随机数a和b,则方程x=-2a-b2x有实根的概率为( )
A.?16??????????????????????????????????????????B.?23??????????????????????????????????????????C.?12??????????????????????????????????????????D.?13
11.利用随机模拟方法计算y=x2+1与y=5围成的面积时,先利用计算器产生两组0~1之间的均匀随机数a1=RAND,b1=RAND,然后进行平移与伸缩变换a=4a1﹣2,b=4b1+1,实验进行了1000次,前998次中落在所求面积区域内的样本点数为624,若最后两次实验产生的0~1之间的均匀随机数为(0.3,0.1),(0.9,0.7),则本次模拟得到的面积的估计值是( )
A.?10?????????????????????????????????????B.?252?????????????????????????????????????C.?1248125?????????????????????????????????????D.?1252125
12.为了测算如图阴影部分的面积,作一个边长为6的正方形将其包含在内,并向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是( )
A.?12???????????????????????????????????????????B.?9???????????????????????????????????????????C.?8???????????????????????????????????????????D.?6
13.利用计算机产生0~1之间的均匀随机数a,则使关于x的一元二次方程x2﹣x+a=0无实根的概率为( )
A.?12??????????????????????????????????????????B.?14??????????????????????????????????????????C.?34??????????????????????????????????????????D.?23
14.如图中,矩形长为6,宽为4,向矩形内随机掷300颗黄豆,数得落在椭圆内的黄豆数204,则一次实验数据为依据估计出椭圆的面积约为( )
A.?7.66???????????????????????????????????B.?16.32???????????????????????????????????C.?17.28???????????????????????????????????D.?8.68
15.如图在区域Ω={(x,y)|﹣2≤x≤2,0≤y≤4}中随机撒900粒豆子,如果落在每个区域的豆子数与这个区域的面积近似成正比,试估计落在图中阴影部分的豆子数为( )
A.?300??????????????????????????????????????B.?400??????????????????????????????????????C.?500??????????????????????????????????????D.?600
16.如图,面积为4的矩形ABCD中有一块阴影部分,若往矩形ABCD中随机投掷1000个点,落在矩形ABCD的非阴影部分中的点数为600个,则据此估计阴影部分的面积为( )
A.?1.2???????????????????????????????????????B.?1.4???????????????????????????????????????C.?1.6???????????????????????????????????????D.?1.8
17.如图,在边长为a的正方形内有图形Ω,现向正方形内撒豆子,若撒在图形Ω内核正方形内的豆子数分别为m,n,则图形Ω面积的估计值为(?? )
A.?man??????????????????????????????????????B.?nam??????????????????????????????????????C.?ma2n??????????????????????????????????????D.?na2m
18.某个游戏中,一个珠子按如图所示的通道,由上至下的滑下,从最下面的六个出口出来,规定猜中者为胜,如果你在该游戏中,猜得珠子从口3出来,那么你取胜的概率为(?? )
A.?516??????????????????????????????????????B.?532??????????????????????????????????????C.?16??????????????????????????????????????D.?都不对
二、解答题
19.近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,先随机抽取了该市三类垃圾箱总计1000吨生活垃圾,数据统计如下(单位:吨);
“厨余垃圾”箱
“可回收物”箱
“其他垃圾”箱
厨余垃圾
400
100
100
可回收物
30
240
30
其他垃圾
20
20
60
(1)试估计厨余垃圾投放正确的概率;
(2)试估计生活垃圾投放错误的概率;
(3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c的方差s2最大时,写出a,b,c的值(结论不要求证明),并求此时s2的值.
(求:S2= 1n ?[ (x1?x)2 + (x2?x)2 +…+ (xn?x)2 ],其中 x 为数据x1 , x2 , …,xn的平均数)
20.利用随机模拟方法估计曲线y=x2与直线x=1及x轴围成的区域面积.
21.为了了解某校高一学生体能情况,抽取200位同学进行1分钟跳绳次数测试,将所得数据整理后画出频率分布直方图(如图所示),请回答下列问题:
(1)次数在100~110之间的频率是多少?
(2)若次数在110以上为达标,试估计该校全体高一学生的达标率是多少?
(3)根据频率分布直方图估计,学生跳绳次数的平均数是多少?
答案解析部分
一、单选题
1.【答案】D
【解析】解:直角三角形的斜边长为 82+152 =17,
设内切圆的半径为r,则8﹣r+15﹣r=17,解得r=3.
∴内切圆的面积为πr2=9π,
∴豆子落在内切圆外部的概率P=1﹣ 9π12×8×15 =1﹣ 3π20 .
故答案为:D.
2.【答案】B
【解析】解:在大正方形内随机取一点,这一点落在小正方形的概率为 15 , 不妨设大正方形面积为5,小正方形面积为1,
∴大正方形边长为 5 ,小正方形的边长为1.
∴四个全等的直角三角形的斜边的长是 5 ,
较短的直角边的长是1,较长的直角边的长是2,
故sinθ= 25=255 ,
故选:B.
3.【答案】A
【解析】解:据残差图显示的分布情况即可看出图1显示的残差分布集中,拟合度较好, 故选A.
4.【答案】B
【解析】解:由题意,由随机模拟方法可得积分 ∫02 1?x24 dx的近似值为 4001000×4 =1.6, 故选B.
5.【答案】 B
【解析】解:根据题意,设阴影部分的面积为S,则正方形的面积为36,
向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,
则向正方形内随机投掷一点,其落到阴影部分的概率P= 200800 = 14 ;
而P= s36 ,则 s36 = 14 ,
解可得,S=9;
故选B.
6.【答案】 B
【解析】解:由题意知模拟打3局比赛甲恰好获胜2局的结果,经随机模拟产生了如下20组随机数,
在30组随机数中表示打3局比赛甲恰好获胜2局的有:102,146,245,310,481,337,139,235,246,共9组随机数,
∴所求概率为 930 = 310 .
故答案为:B.
7.【答案】 B
【解析】解:设阴影外部分的面积为s,
则由几何概型的概率公式得: ,
解得s=57,
可以估计出阴影部分的面积约为100﹣57=43.
故选:B.
8.【答案】 A
【解析】解:设区域面积为x,
由概率的几何概型知,则 3021000=x2 ,
解得x=0.604.
则该区域面积的近似值为0.604,
故选:A.
9.【答案】 B
【解析】解:由题意知模拟三次投篮的结果,经随机模拟产生了如下20组随机数,
在20组随机数中表示三次投篮恰有两次命中的有:191、271、932、812、393.
共5组随机数,
∴所求概率为 520=14 =0.25.
故选B.
10.【答案】 C
【解析】解:由题意知本题是一个几何概型,x=-2a-b2x
化为x2+2ax+b2=0,方程有实根,△≥0
即4a2﹣4b2≥0
∴b≤a.
在aOb坐标系中画出图形.如图.∴方程有实根的概率为P=
故选C.
11.【答案】 A
【解析】解:由a1=0.3,b1=0.1得a=﹣0.8,b=1.4,(﹣0.8,1.4)落在y=x2+1与y=5围成的区域内,
由a1=0.9,b1=0.7得:a=1.6,b=3.8,(1.6,3.8)落在y=x2+1与y=5围成的区域外,
所以本次模拟得出的面积为 16×6251000=10.
故选:A
12.【答案】 B
【解析】解:根据题意,设阴影部分的面积为S,则正方形的面积为36,
向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,
则向正方形内随机投掷一点,其落到阴影部分的概率P= 200800=14;
?,
解可得,S=9;
故选B.
.
13.【答案】 C
【解析】解:∵关于x的一元二次方程x2﹣x+a=0无实根,
∴△=1﹣4a<0,
∵0<a<1,
∴14
故选:C.
14.【答案】 B
【解析】解:黄豆落在椭圆外的概率为: 204300=24?S24
解得:S=16.32.
故选:B.
15.【答案】 D
【解析】解:区域Ω的面积为S1=16.
图中阴影部分的面积:S2=S1﹣2.
设落在阴影部分的豆子数为m,由已知条件, 即m=600.
因此落在图中阴影部分的豆子约为600粒.
16.【答案】 C
【解析】解:根据几何概率的计算公式可得,向距形内随机投掷1000个点,落在矩形ABCD的非阴影部分中的点数为600个,则落在矩形ABCD的阴影部分中的点数为400个,
设阴影部分的面积为S,落在阴影部分为事件A,
∴落在阴影部分的概率P(A)= , 解得S=1.6.
故选C.
17.【答案】 C
【解析】解:如图,在边长为a的正方形内有图形Ω,则正方形的面积为a2 ,
现向正方形内撒豆子,
若撒在图形Ω内和正方形内的豆子数分别为m,n,
则图形Ω面积的估计值为: mn×a2 = ma2n .
故答案为:C.
18.【答案】 A
【解析】所求的概率为 P=C5225=516 ?,故选A.
二、解答题
19.【答案】 (1)解:由题意可知:厨余垃圾600吨,投放到“厨余垃圾”箱400吨,故厨余垃圾投放正确的概率为 400600=23
(2)解:由题意可知:生活垃圾投放错误有200+60+20+20=300,故生活垃圾投放错误的概率为 3001000=310
(3)解:由题意可知:∵a+b+c=600,∴a,b,c的平均数为200
∴ s2=13[(a?200)2+(b?200)2+(c?200)2] = 13(a2+b2+c2?120000) ,
∵(a+b+c)2=a2+b2+c2+2ab+2bc+2ac≥a2+b2+c2 , 因此有当a=600,b=0,c=0时,有s2=80000
【解析】(1)厨余垃圾600吨,投放到“厨余垃圾”箱400吨,故可求厨余垃圾投放正确的概率;(2)生活垃圾投放错误有200+60+20+20=300,故可求生活垃圾投放错误的概率;(3)计算方差可得 s2=13[(a?200)2+(b?200)2+(c?200)2] = 13(a2+b2+c2?120000) ,因此有当a=600,b=0,c=0时,有s2=80000.
20.【答案】 解:(1)利用计算机分别产生[0,1]和[0,1]上的均匀随机数:a=Rand和b=Rand,得随机数组(a,b).
(2)统计试验总次数N和落在“曲边梯形”内的点数N1(满足b<a2的点(a,b)数)
(3)计算频率 N1N , 得点落在“曲边梯形”上的概率近似值.
(4)由几何概型得p=S1 , 所以N1N=S1 , 于是得到S=N1N , 这就是“曲边梯形”面积的近似值.
【解析】先由计算器做模拟试验结果试验估计,满足条件b<a2的点(a,b)的概率,再转化为几何概型的面积类型求解.
21.【答案】 (1)∵第二组面积为0.02×10=0.2,
∴次数在100~110之间的频率是0.2.
∵第二小组频数为12;
(2)∵次数在110以上(含110次)为达标,
∴高一学生的达标率是 10×(0.035+0.025+0.015)=75%
即高一有75%的学生达标.
(3)根据频率分布直方图估计,学生跳绳次数的平均数是95×0.05+105×0.2+115×0.35+125×0.25+135×0.15=117.5.
【解析】(1)根据第二组小矩形的面积,做出第二组的频率.
(2)从频率分步直方图中看出次数子啊110以上的频数,用频数除以样本容量得到达标率,进而估计高一全体学生的达标率.
(3)将每组的组中值乘以该组的频率即可求出学生跳绳次数的平均数.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
