山东省枣庄市薛城区2020-2021学年高一下学期期中考试数学试题 Word版含答案
文档属性
| 名称 | 山东省枣庄市薛城区2020-2021学年高一下学期期中考试数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 1006.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-03 06:25:04 | ||
图片预览



文档简介
秘密★启用前 试卷类型:A
枣庄市薛城区2020-2021学年下学期期中检测
高 一 数 学
2021.04
本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页,满分为150分,考试时间120分钟.
第I卷(选择题 共60分)
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷规定的位置上.
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.
3.第Ⅱ卷必须将答案写在答题卡各题目指定区域内相应的位置;如需改动,先划掉原来的答案,然后再写上新的答案. 写在本试卷上无效.
一、单项选择题:本题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数. 则在复平面内,对应的点的坐标是
A. B. C. D.
2.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是
A.25π B.50π C.125π D.都不对
3.向量在正方形网格中的位置如图所示.若向量
与垂直,则实数
A. B.
C.3 D.2
4.设是所以平面内一点,,则
A. B.
C. D.
5.如果一个水平放置的图形的斜二测直观图是一个底面为,腰和上底均为1的等腰梯形,那么原平面图形的面积是
A. B. C. D.
6.已知圆柱的高为,它的两个底面的圆周在同一个半径为的球的球面上. 则球的体积与圆柱的体积的比值为
A. B. C. D.
7.《数书九章》是中国南宋时期杰出数学家秦九韶的著作,全书十八卷共八十一个问题,分为九类,每类九个问题,《数书九章》中记录了秦九昭的许多创造性成就,其中在卷五“三斜求职”中提出了已知三角形三边求面积的公式,这与古希腊的海伦公式完全等价,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实,一为从隅,开平方得积.”若把以上这段文字写成公式,
即,现在有周长为的满足
,则用以上给出的公式求得的面积为
A. B. C. D. 12
8.如图,是某防汛抗洪大坝的坡面,大坝上有一高为20米的监测塔,若某科研小组在坝底点测得,沿着坡面前进40米到达点,测得,则大坝的坡角()的余弦值为
A. B.
C. D.
二、多项选择题:本题共4小题,每小题5分,共20分. 在每小题给出的选项中,有多项符合题目要求. 全部选对的得5分,部分选对的得2分,有选错的得0分.
9.用一个平面去截一个几何体,截面的形状是三角形,那么这个几何体可能是
A. 圆锥 B. 圆柱 C. 棱锥 D. 正方体
10.已知复数的共轭复数为,且,则下列结论正确的是
A. B. 虚部为 C. D.
11.在中,,,分别是边,,的中点,下列说法正确的是
A. B.
C. 若,则是在的投影向量
D. 若点是线段上的动点,且满足,则的最大值为
12.对于,有如下命题,其中正确的有
A.若,则是等腰三角形
B.若是锐角三角形,则不等式恒成立
C.若,则为锐角三角形
D.若,则为钝角三角形
第II卷(非选择题 共90分)
三.填空题:本题共4小题,每小题5分,共20分.
13.已知向量,,则在方向上的投影向量的模为________.
14.△ABC的内角为A,B,C所对应的边分别为a,b,c,已知a=2,c=,A=30°,则边长b= .
15.如图,在四边形ABCD中,=3,E为边BC的中点,若=+,则λ+μ=_________.
16.如图是一座山的示意图,山呈圆锥形,圆锥的底面半径为10公里,母线长为40公里,是母线上一点,且公里.为了发展旅游业,要建设一条最短的从绕山一周到的观光铁路.这条铁路从出发后首先上坡,随后下坡,则下坡段铁路的长度为 公里.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题共10分)
已知复平面内的点A,B对应的复数分别为,(),设对应的复数为z.
(1)当实数m取何值时,复数z是纯虚数;
(2)若复数z在复平面上对应的点位于第四象限,求实数m的取值范围.
18.(本小题共12分)
已知向量,,.
(1)求向量与所成角的余弦值;
(2)若//,求实数的值.
19.(本小题共12分)
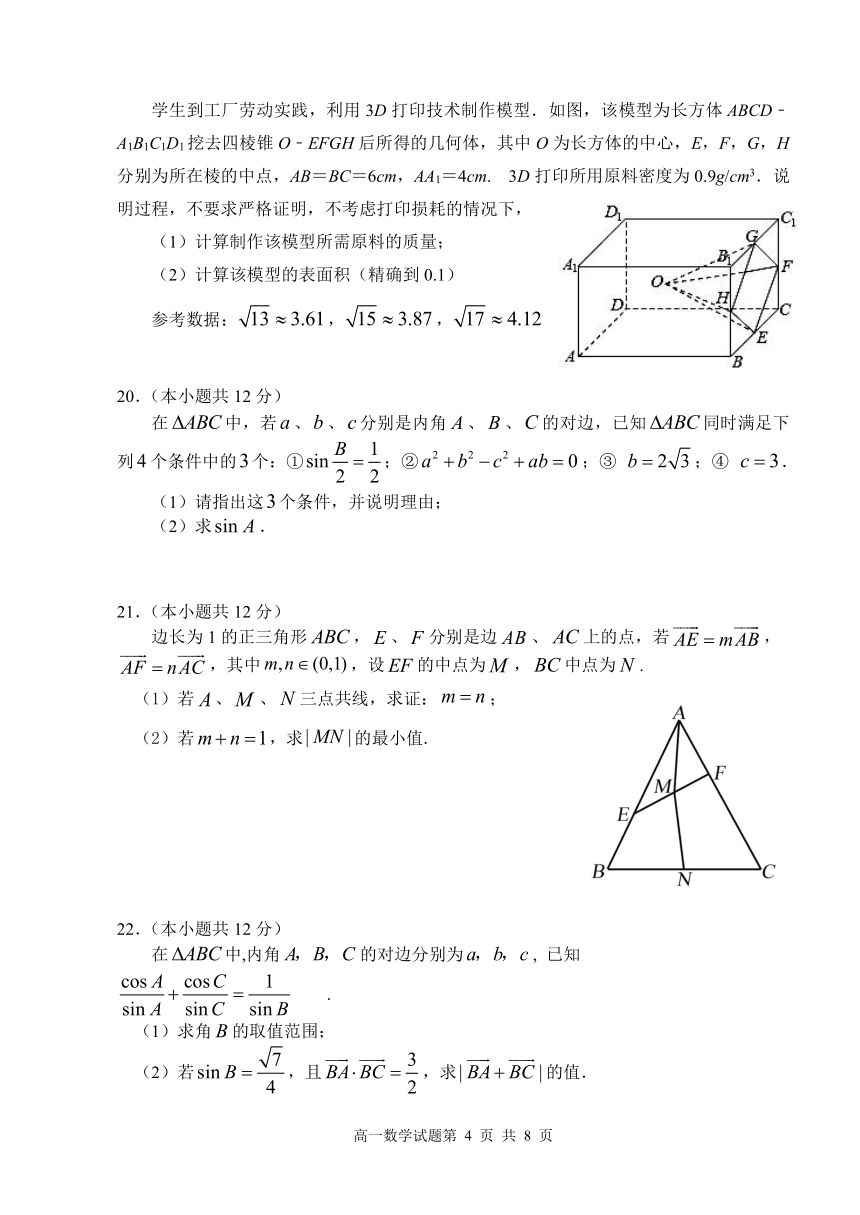
学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD﹣A1B1C1D1挖去四棱锥O﹣EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6cm,AA1=4cm. 3D打印所用原料密度为0.9g/cm3.说明过程,不要求严格证明,不考虑打印损耗的情况下,
计算制作该模型所需原料的质量;
计算该模型的表面积(精确到0.1)
参考数据:,,
20.(本小题共12分)
在中,若、、分别是内角、、的对边,已知同时满足下列个条件中的个:①;②;③ ;④ .
(1)请指出这个条件,并说明理由;
(2)求.
21.(本小题共12分)
边长为1的正三角形,、分别是边、上的点,若,,其中,设的中点为,中点为.
(1)若、、三点共线,求证:;
(2)若,求的最小值.
22.(本小题共12分)
在中,内角的对边分别为, 已知.
(1)求角的取值范围;
(2)若,且,求的值.
2020~2021学年度模块检测试题
高一数学试题参考答案及评分标准 2021.04
一、单项选择题(本题共8小题,每小题5分,共40分)
1~4 BBDD 5~8 ADAA
二.多项选择题(本题共4小题,每小题5分,共20分)
9. ACD 10. AD 11. BCD 12. BD
三、填空题(本题共4小题,每小题5分,共20分)
13. 14.或 15. 16.
四、解答题(本题共6小题,共70分)
17. 解:点A,B对应的复数分别为,
对应的复数为z,
.
(1)复数z是纯虚数,, 3分
解得,. 5分
(2)复数z在复平面上对应的点坐标为,
位于第四象限,, 7分
即,. 10分
解:(1)因为,,所以.2分
设向量与所成角为,
. 6分
(2)∵ ,, 8分
又 //,
∴,解得. 12分
19 . 解:(1)因为E,F,G,H,分别为所在矩形各棱的中点,所以四边形EFGH为菱形.
由AB=BC=6cm,AA1=4cm,得
又因为O为长方体的中心,所四棱锥O﹣EFGH的高. 2分
,
. 4分
∴该模型体积为:
cm3. 5分
∵3D打印所用原料密度为0.9g/cm3,不考虑打印损耗,
∴制作该模型所需原料的质量为:132×0.9=118.8g. 6分
(2)记面的中心为,连接,,,
则,,. 8分
由题意,四棱锥O﹣EFGH的四个侧面为全等三角形.
在等腰中,取的中点,连接,
,
所以. 10分
∴该模型表面积为:
cm3
cm2. 12分
20.解:(1)同时满足条件①,③,④. 1分
理由如下:
若同时满足①,②.
因为,且,所以,即 2分
因为,且,所以 4分
所以,矛盾 5分
所以只能同时满足③,④.
因为,所以,故不满足②
故满足①,③,④ 7分
(2)在中,,,
又由正弦定理知:,所以 9分
又因为,所以, 10分
所以 12分
21. 解:(1)由三点共线,得共线,
根据共线向量定理可得,存在使得,
即, ………… 3分
所以,
根据平面向量基本定理可得,
所以. ……………… 5分
(2)因为
. 7分
又,所以. 8分
因为三角形是边长为1的正三角形,所以,, 9分
所以
. 11分
所以时,取得最小值. 12分
22. 解:(1)因为
. 2分
所以
由正弦定理可得,. 4分
因为,
所以,即 . 6分
(2)因为,且,所以B不是最大角,
所以.
所以,得.因而. 8分
由余弦定理得,所以. 10分
所以 ,
即. 12分
高一数学试题第 1 页 共 10 页
枣庄市薛城区2020-2021学年下学期期中检测
高 一 数 学
2021.04
本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页,满分为150分,考试时间120分钟.
第I卷(选择题 共60分)
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷规定的位置上.
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.
3.第Ⅱ卷必须将答案写在答题卡各题目指定区域内相应的位置;如需改动,先划掉原来的答案,然后再写上新的答案. 写在本试卷上无效.
一、单项选择题:本题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数. 则在复平面内,对应的点的坐标是
A. B. C. D.
2.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是
A.25π B.50π C.125π D.都不对
3.向量在正方形网格中的位置如图所示.若向量
与垂直,则实数
A. B.
C.3 D.2
4.设是所以平面内一点,,则
A. B.
C. D.
5.如果一个水平放置的图形的斜二测直观图是一个底面为,腰和上底均为1的等腰梯形,那么原平面图形的面积是
A. B. C. D.
6.已知圆柱的高为,它的两个底面的圆周在同一个半径为的球的球面上. 则球的体积与圆柱的体积的比值为
A. B. C. D.
7.《数书九章》是中国南宋时期杰出数学家秦九韶的著作,全书十八卷共八十一个问题,分为九类,每类九个问题,《数书九章》中记录了秦九昭的许多创造性成就,其中在卷五“三斜求职”中提出了已知三角形三边求面积的公式,这与古希腊的海伦公式完全等价,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实,一为从隅,开平方得积.”若把以上这段文字写成公式,
即,现在有周长为的满足
,则用以上给出的公式求得的面积为
A. B. C. D. 12
8.如图,是某防汛抗洪大坝的坡面,大坝上有一高为20米的监测塔,若某科研小组在坝底点测得,沿着坡面前进40米到达点,测得,则大坝的坡角()的余弦值为
A. B.
C. D.
二、多项选择题:本题共4小题,每小题5分,共20分. 在每小题给出的选项中,有多项符合题目要求. 全部选对的得5分,部分选对的得2分,有选错的得0分.
9.用一个平面去截一个几何体,截面的形状是三角形,那么这个几何体可能是
A. 圆锥 B. 圆柱 C. 棱锥 D. 正方体
10.已知复数的共轭复数为,且,则下列结论正确的是
A. B. 虚部为 C. D.
11.在中,,,分别是边,,的中点,下列说法正确的是
A. B.
C. 若,则是在的投影向量
D. 若点是线段上的动点,且满足,则的最大值为
12.对于,有如下命题,其中正确的有
A.若,则是等腰三角形
B.若是锐角三角形,则不等式恒成立
C.若,则为锐角三角形
D.若,则为钝角三角形
第II卷(非选择题 共90分)
三.填空题:本题共4小题,每小题5分,共20分.
13.已知向量,,则在方向上的投影向量的模为________.
14.△ABC的内角为A,B,C所对应的边分别为a,b,c,已知a=2,c=,A=30°,则边长b= .
15.如图,在四边形ABCD中,=3,E为边BC的中点,若=+,则λ+μ=_________.
16.如图是一座山的示意图,山呈圆锥形,圆锥的底面半径为10公里,母线长为40公里,是母线上一点,且公里.为了发展旅游业,要建设一条最短的从绕山一周到的观光铁路.这条铁路从出发后首先上坡,随后下坡,则下坡段铁路的长度为 公里.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题共10分)
已知复平面内的点A,B对应的复数分别为,(),设对应的复数为z.
(1)当实数m取何值时,复数z是纯虚数;
(2)若复数z在复平面上对应的点位于第四象限,求实数m的取值范围.
18.(本小题共12分)
已知向量,,.
(1)求向量与所成角的余弦值;
(2)若//,求实数的值.
19.(本小题共12分)
学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD﹣A1B1C1D1挖去四棱锥O﹣EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6cm,AA1=4cm. 3D打印所用原料密度为0.9g/cm3.说明过程,不要求严格证明,不考虑打印损耗的情况下,
计算制作该模型所需原料的质量;
计算该模型的表面积(精确到0.1)
参考数据:,,
20.(本小题共12分)
在中,若、、分别是内角、、的对边,已知同时满足下列个条件中的个:①;②;③ ;④ .
(1)请指出这个条件,并说明理由;
(2)求.
21.(本小题共12分)
边长为1的正三角形,、分别是边、上的点,若,,其中,设的中点为,中点为.
(1)若、、三点共线,求证:;
(2)若,求的最小值.
22.(本小题共12分)
在中,内角的对边分别为, 已知.
(1)求角的取值范围;
(2)若,且,求的值.
2020~2021学年度模块检测试题
高一数学试题参考答案及评分标准 2021.04
一、单项选择题(本题共8小题,每小题5分,共40分)
1~4 BBDD 5~8 ADAA
二.多项选择题(本题共4小题,每小题5分,共20分)
9. ACD 10. AD 11. BCD 12. BD
三、填空题(本题共4小题,每小题5分,共20分)
13. 14.或 15. 16.
四、解答题(本题共6小题,共70分)
17. 解:点A,B对应的复数分别为,
对应的复数为z,
.
(1)复数z是纯虚数,, 3分
解得,. 5分
(2)复数z在复平面上对应的点坐标为,
位于第四象限,, 7分
即,. 10分
解:(1)因为,,所以.2分
设向量与所成角为,
. 6分
(2)∵ ,, 8分
又 //,
∴,解得. 12分
19 . 解:(1)因为E,F,G,H,分别为所在矩形各棱的中点,所以四边形EFGH为菱形.
由AB=BC=6cm,AA1=4cm,得
又因为O为长方体的中心,所四棱锥O﹣EFGH的高. 2分
,
. 4分
∴该模型体积为:
cm3. 5分
∵3D打印所用原料密度为0.9g/cm3,不考虑打印损耗,
∴制作该模型所需原料的质量为:132×0.9=118.8g. 6分
(2)记面的中心为,连接,,,
则,,. 8分
由题意,四棱锥O﹣EFGH的四个侧面为全等三角形.
在等腰中,取的中点,连接,
,
所以. 10分
∴该模型表面积为:
cm3
cm2. 12分
20.解:(1)同时满足条件①,③,④. 1分
理由如下:
若同时满足①,②.
因为,且,所以,即 2分
因为,且,所以 4分
所以,矛盾 5分
所以只能同时满足③,④.
因为,所以,故不满足②
故满足①,③,④ 7分
(2)在中,,,
又由正弦定理知:,所以 9分
又因为,所以, 10分
所以 12分
21. 解:(1)由三点共线,得共线,
根据共线向量定理可得,存在使得,
即, ………… 3分
所以,
根据平面向量基本定理可得,
所以. ……………… 5分
(2)因为
. 7分
又,所以. 8分
因为三角形是边长为1的正三角形,所以,, 9分
所以
. 11分
所以时,取得最小值. 12分
22. 解:(1)因为
. 2分
所以
由正弦定理可得,. 4分
因为,
所以,即 . 6分
(2)因为,且,所以B不是最大角,
所以.
所以,得.因而. 8分
由余弦定理得,所以. 10分
所以 ,
即. 12分
高一数学试题第 1 页 共 10 页
同课章节目录
