人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)课件(43张PPT)
文档属性
| 名称 | 人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)课件(43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-06 10:26:01 | ||
图片预览











文档简介
(共43张PPT)
人教版六年级数学下册第三章
《圆柱与圆锥》知识讲解及考前押题卷精讲
(第四套)
专题复习课件
知识讲解
01
第一部分 知识讲解
一、圆柱
1、圆柱的形成:圆柱是以长方形的一边为轴旋转而得到的。
圆柱也可以由长方形卷曲而得到。(两种方式:1.以长方形的长为底面周长,宽为高;2.以长方形的宽为底面周长,长为高。其中,第一种方式得到的圆柱体体积较大。)
2、圆柱的高是两个底面之间的距离,一个圆柱有无数条高,他们的数值是相等的
3、圆柱的特征:
(1)底面的特征:圆柱的底面是完全相等的两个圆。
(2)侧面的特征:圆柱的侧面是一个曲面。
(3)高的特征 :圆柱有无数条高
4、圆柱的切割:①横切:切面是圆,表面积增加2倍底面积,即S 增 =2πr2
②竖切(过直径):切面是长方形(如果h=2R,切面为正方形),该长方形的长是圆柱的高,宽是圆柱的底面直径,表面积增加两个长方形的面积,即S增=4rh
第一部分 知识讲解
5、圆柱的侧面展开图:①沿着高展开,展开图形是长方形,如果h=2πr,展开图形为正方形
②不沿着高展开,展开图形是平行四边形或不规则图形
③无论怎么展开都得不到梯形
6、圆柱的相关计算公式:底面积 :S底=πr2
底面周长:C底=πd=2πr
侧面积 :S侧=2πrh
表面积 :S表=2S底+S侧=2πr2+2πrh
体积 :V柱=πr2h
考试常见题型:①已知圆柱的底面积和高, 求圆柱的侧面积,表面积,体积,底面周长
②已知圆柱的底面周长和高,求圆柱的侧面积,表面积,体积,底面积
③已知圆柱的底面周长和体积,求圆柱的侧面积,表面积,高,底面积
④已知圆柱的底面面积和高,求圆柱的侧面积,表面积,体积
第一部分 知识讲解
⑤已知圆柱的侧面积和高, 求圆柱的底面半径,表面积,体积,底面积
以上几种常见题型的解题方法,通常是求出圆柱的底面半径和高,再根据圆柱的相关计算公式进行计算
无盖水桶的表面积 =侧面积+一个底面积
油桶的表面积=侧面积+两个底面积
烟囱通风管的表面积=侧面积
只求侧面积:灯罩、排水管、漆柱、通风管、压路机、卫生纸中轴、薯片盒包装
侧面积+一个底面积:玻璃杯、水桶、笔筒、帽子、游泳池
侧面积+两个底面积:油桶、米桶、罐桶类
二、圆锥
1、圆柱的形成:圆锥是以直角三角形的一直角边为轴旋转而得到的
圆锥也可以由扇形卷曲而得到
第一部分 知识讲解
第一部分 知识讲解
2、圆锥的高是两个顶点与底面之间的距离,与圆柱不同,圆锥只有一条高
3、圆锥的特征:
(1)底面的特征:圆锥的底面一个圆。
(2)侧面的特征:圆锥的侧面是一个曲面。
(3)高的特征 :圆锥有一条高。
4、圆柱的切割:①横切:切面是圆
②竖切(过顶点和直径直径):切面是等腰三角形,该等腰三角形的高是圆锥的高,底是圆锥的底面直径,面积增加两个等腰三角形的面积,即S增=2rh
5、圆锥的相关计算公式:底面积 :S底=πr2
底面周长:C底=πd=2πr
体积:V锥= πr2h
考试常见题型:①已知圆锥的底面积和高,求体积,底面周长
第一部分 知识讲解
②已知圆锥的底面周长和高,求圆锥的体积,底面积
③已知圆锥的底面周长和体积,求圆锥的高,底面积
以上几种常见题型的解题方法,通常是求出圆锥的底面半径和高,再根据圆柱的相关计算公式进行计算。
1、圆柱与圆锥等底等高,圆柱的体积是圆锥的3倍。
2、圆柱与圆锥等底等体积,圆锥的高是圆柱的3倍。
3、圆柱与圆锥等高等体积,圆锥的底面积(注意:是底面积而不是底面半径)是圆柱的3倍。
4、圆柱与圆锥等底等高 ,体积相差 Sh
题型总结
①直接利用公式:分析清楚求的的是表面积,侧面积、底面积、体积
分析清楚半径变化导致底面周长、侧面积、底面积、体积的变化
分析清楚两个圆柱(或两个圆锥)半径、底面积、底面周长、侧面积、表面积、体积之比
第一部分 知识讲解
②圆柱与圆锥关系的转换:包括削成最大体积的问题(正方体,长方体与圆柱圆锥之间)
③横截面的问题
④浸水体积问题:(水面上升部分的体积就是浸入水中物品的体积,等于盛水容积的底面积乘以上升的高度)容积是圆柱或长方体,正方体
⑤等体积转换问题:一个圆柱融化后做成圆锥,或圆柱中的溶液倒入圆锥,都是体积不变的 问题,注意不要乘以
考前押题卷精讲
(全解析)
02
第二部分 学习检测
05
讲解脉络
01
02
03
04
选择题
判断题
填空题
解答题
一.单选题
1.圆柱体,上下两个面是( )
A. 长方形 B. 正方形 C. 圆 D. 三角形
C
【答案】C
【分析】根据圆柱的概念来判断。圆柱是由两个大小相等、相互平行的圆形(底面)以及连接两个底面的一个曲面(侧面)围成的几何体
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
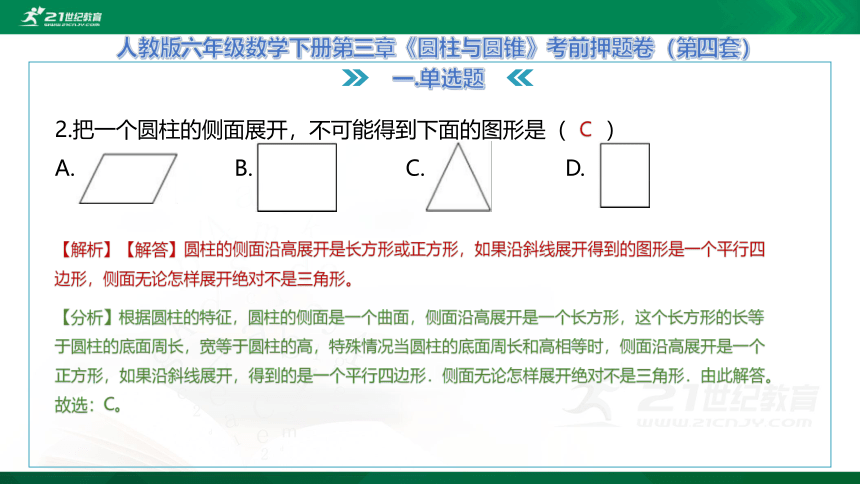
2.把一个圆柱的侧面展开,不可能得到下面的图形是( )
A. B. C. D.
一.单选题
C
【解析】【解答】圆柱的侧面沿高展开是长方形或正方形,如果沿斜线展开得到的图形是一个平行四边形,侧面无论怎样展开绝对不是三角形。
【分析】根据圆柱的特征,圆柱的侧面是一个曲面,侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高,特殊情况当圆柱的底面周长和高相等时,侧面沿高展开是一个正方形,如果沿斜线展开,得到的是一个平行四边形.侧面无论怎样展开绝对不是三角形.由此解答。
故选:C。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
3.一个圆柱体,侧面展开后得到一个正方形,它的高是底面半径的( )倍.
A. 2 B. 2π C. π
一.单选题
B
【解析】【解答】 一个圆柱体,侧面展开后得到一个正方形,它的高是底面半径的:2πr÷r=2π倍.
故答案为:B.
【分析】一个圆柱体,侧面展开后得到一个正方形,它的高与底面周长相等,圆柱的底面周长C=2πr,也就是高是2πr,然后用圆柱的高÷底面半径=倍数,据此列式解答.
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
4.求一个圆柱形水桶能盛多少水,就是求这个水桶的( )。
A. 侧面积 B. 表面积 C. 容积
一.单选题
C
【解析】【解答】解:求一个圆柱形水桶能盛多少水,就是求这个水桶的容积。
故答案为:C。
【分析】容积是物体所能容纳物体的体积,由此判断并选择即可。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
5.右图中,大圆锥的底面半径是小圆锥的2倍,高也是小圆锥的2倍,大圆
锥的体积是小圆锥的( )倍。
A.2 B.4 C.6 D.8
一.单选题
D
【解析】【解答】2x2x2=8
故答案为:D
【分析】从题中条件可知,大圆锥的底面半径是小圆锥的2倍,那么,大圆锥的底面积就是小圆锥底面积的4倍,圆锥的体积=底面积x高x1/3 , 圆锥体积的大小跟圆锥底面积和高有关。因此,大圆锥体积是小圆锥体积的8倍。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
6.在下面的图形中,以直线为轴旋转,可以得到圆锥的是( )。
A. B. C. D.
一.单选题
C
【解析】【解答】 在下面的图形中,以直线为轴旋转,可以得到圆锥的是 .
故答案为:C.
【分析】一个直角三角形以一条直角边为轴,旋转一周,得到的图形是圆锥,据此解答.
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
一.单选题
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
7.一个圆柱与一个圆锥的体积和底面积都相等,圆柱的高是圆锥的( )。
A. 2倍 B. C. 3倍 D.
B
【解析】【解答】 一个圆柱与一个圆锥的体积和底面积都相等,圆柱的高是圆锥的 倍。 故答案为:B。
【分析】 圆柱的体积公式为: V=Sh,圆柱的体积公式为: V= Sh,根据圆柱与圆锥体积的关系:等底等高的圆柱和圆锥,圆柱的体积是圆锥的3倍,圆锥的体积是圆柱的 , 推出圆柱与圆锥的底面积关系为:圆柱的高是圆锥的 倍,由此可得出答案。
8.圆柱的底面半径扩大到原来的2倍,高也扩大到原来的2倍,体积( )
A. 扩大到原来的4倍 B. 不变 C. 扩大到原来的8倍 D. 不能确定
一.单选题
C
【解析】【解答】 圆柱的底面半径扩大到原来的2倍,高也扩大到原来的2倍,体积扩大到原来的8倍。
故答案为:C。
【分析】圆柱的体积公式:V=πr2h,圆柱的底面半径扩大到原来的a倍,高也扩大到原来的a倍,体积扩大到原来的a3倍。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
9.把一根长1米,底面积为3.14平方米的圆柱锯成两个小圆柱,它的表面积( )
A. 增加3.14平方米 B. 减少3.14平方米
C. 增加6.28平方米 D. 减少6.28平方米
一.单选题
C
【解析】【解答】切割后表面积增加了:3.14×2=6.28(平方米)
【分析】把圆柱切割成2个小圆柱后,表面积增加了2个圆柱的底面积,由此即可解答。
故选:C
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
10.一个圆柱和一个圆锥,底面周长的比是2:3,体积比是5:6,那么这个圆柱和圆锥高的最简单的整数比是( )
A. 8:5 B. 5:8 C. 12:5 D. 5:12
一.单选题
B
【解析】【解答】解:底面半径的比也是2:3。高的比:
故答案为:B。
【分析】底面周长的比与底面半径的比相等,把圆柱的底面半径看作2,体积看作5,圆锥的底面半径看作3,体积看作6;根据体积公式分别表示出圆柱的高和圆锥的高,然后写出高的最简整数比即可。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
11.圆柱和圆锥都有无数条高。 ( )
二.判断题
错误
【解析】【解答】圆柱有无数条高,圆锥只有一条高,原题说法错误.
故答案为:错误.
【分析】根据圆柱和圆锥高的定义:圆柱的上、下底面之间的距离叫做圆柱的高,圆柱的高有无数条;从圆锥的顶点到底面圆心的距离叫做圆锥的高,圆锥只有1条高,据此判断.
12.一个圆锥的侧面展开图是一个三角形。 ( )
【解析】【解答】解:一个圆锥的侧面展开图是一个扇形,原题说法错误.
故答案为:错误
【分析】圆锥是由一个圆形的底面和一个曲面组成的,曲面展开后是一个扇形.
错误
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
13.圆锥的体积一定等于圆柱的 1/3 。 ( )
二.判断题
错误
【答案】 错误
【分析】这里没有指出圆锥与圆柱的底与高。
14.一个圆柱的直径和高相等,则圆柱体的侧面展开图是正方形。 ( )
【解答】解:设一个圆柱的直径为d厘米,高也为d厘米。
底面周长=d ;因d >d,故侧面展开图不是正方形。
故答案为:错误。
【分析】如果一个圆柱的底面周长和高相等,那么圆柱体的侧面展开图就是正方形。
错误
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
15.一张长方形铁皮分别横着、竖着卷成两个圆柱,把它们竖放在桌面上,它们的容积完全相同。( )
二.判断题
错误
【解析】【解答】解: 一张长方形铁皮分别横着、竖着卷成两个圆柱,把它们竖放在桌面上,它们的容积不相同。原题说法错误。
故答案为:错误。
【分析】卷成的两个圆柱的底面积和高都不同,不能确定他们的容积是相等的。只能说它们的侧面积相等。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
16.圆柱的上、下底面是两个面积相等的________形.圆柱的侧面是一个________,沿着高展开后可能是一个________形,也可能是一个________形.
三.填空题
长方
【解析】【解答】解:圆柱的上、下底面是两个面积相等的圆形,圆柱的侧面是一个曲面,沿着高展开后可能是一个长方形,也可能是一个正方形。
故答案为:圆;曲面;长方;正方。
【分析】圆柱的两个底面是圆形,侧面是一个曲面,侧面沿着高展开后是一个长方形或正方形,圆柱的底面周长与高相等,侧面展开就是一个正方形。
圆
曲面
正方
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
17.________绕它的一条边旋转一周可以形成圆柱,直角三角形绕它的一条直角边旋转一周可以形成________.
三.填空题
长方形
【解析】【解答】 长方形绕它的一条边旋转一周可以形成圆柱,直角三角形绕它的一条直角边旋转一周可以形成圆锥.
故答案为:长方形;圆锥.
【分析】长方形绕长或宽为轴旋转一周可以形成圆柱,直角三角形绕它的一条直角边旋转一周可以形成圆锥,据此解答.
圆锥
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
18.圆锥的底面是个________形,从圆锥的顶点到底面圆心的距离叫做圆锥的________。
三.填空题
圆
【解析】【解答】解:圆锥的底面是个圆形,从圆锥的顶点到底面圆心的距离叫做圆锥的高。
故答案为:圆;高。
【分析】根据圆锥的特征作答即可。
高
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
19.一个圆柱和一个圆锥等底等高,圆柱与圆锥的体积之和是60立方厘米,圆柱的体积是________立方厘米,圆锥的体积是________立方厘米。
三.填空题
45
15
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
【解析】【解答】圆柱的体积:
60÷(1+ )
=60÷
=60×
=45(立方厘米);
圆锥的体积:45× =15(立方厘米).
故答案为:45;15.
【分析】根据题意可知,等底等高的圆锥体积是圆柱体积的 , 把圆柱的体积看作单位“1”,则圆锥的体积是 , 用圆柱和圆锥的体积之和÷(1+ )=圆柱的体积,然后用圆柱的体积× =圆锥的体积,据此列式解答.
20.计算下列圆柱的表面积.
表面积是________
三.填空题
182.12
【解析】【解答】3.14×(4÷2) ×2+3.14×4×12.5
=25.12+157
=182.12(平方分米)
故答案为:182.12
【分析】根据圆面积公式计算底面积,用底面周长乘高求出圆柱的侧面积,用侧面积加上底面积的2倍即可求出表面积.
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
21.一个底面直径和高都是3分米的圆锥,它的体积是________立方分米,一个与它等底等高的圆柱的体积比它大________立方分米.
三.填空题
7.065
14.13
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
【解析】【解答】解: x 3.14× ×3,
= ×3.14× ×3,
=7.065(立方分米),
7.065×2=14.13(立方分米),
答:它的体积是7.065立方分米,一个与它等底等高的圆柱的体积比它大 14.13立方分米.
故答案为:7.065;14.13.
【分析】(1)利用圆锥的体积= πr2×h,代入数据即可解决问题;(2)等底等高的圆柱的体积是圆锥的体积的3倍,所以与它等底等高的圆柱就比这个圆锥大了它的2倍,由此即可解决问题.
22.一根1米长的圆柱体钢材,截去2分米的一段后,表面积减少25.12平方分米,原来这根钢材的体积是________立方分米.
三.填空题
125.6
【解析】【解答】1米=10分米;25.12÷2÷3.14÷2=2(分米);3.14×2 ×10=125.6(立方分米)。
故答案为:125.6.
【分析】25.12是长为2分米的圆柱的侧面积;侧面积÷长=底面周长;底面周长÷π÷2=底面半径;π×底面半径的平方×高=圆柱体积。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
23.一个正方体木块的棱长是6dm , 把它削成一个最大的圆柱体,圆柱体的体积是________dm3 , 再把这个圆柱体削成一个最大的圆锥体,圆锥体的体积是________dm3 .
三.填空题
169.56
【解析】【解答】6÷2=3(dm)
3.14×32×6
=3.14×9×6
=169.56(dm3)
169.56× =56.52(dm3)
故答案为:169.56;56.52。
【分析】将一个正方体木块削成一个最大的圆柱体,圆柱体的底面直径和高是正方体的棱长,要求圆柱的体积,用公式:V=πr2h,据此列式解答;
把一个圆柱体削成一个最大的圆锥体,圆锥的体积是等底等高的圆柱体积的1/3, 据此列式解答。
56.52
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
三.填空题
25.施灵为了测量萝卜的体积,先将一个萝卜削成一个长5厘米、宽4厘米、高2厘米的长方体,并用天平称出这个长方体重20克.接着用天平称出要测量体积的萝卜重320克.这个萝卜的体积是________立方厘米?
【解析】【解答】320÷[20÷(5×4×2)]
=320÷[20÷40]
=320÷0.5
=640(立方厘米)
【分析】先根据长方体的体积公式V=abh,求出长方体萝卜的体积,即5×4×2=40立方厘米,用20除以40,求出1立方厘米重多少克,再用320除以1立方厘米萝卜的重量,即可求出这个萝卜的体积是多少立方厘米,列式解答即可。
640
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
【解析】【解答】圆锥的体积公式用字母表示:V= Sh .
故答案为:V= Sh。
24.计算圆锥体积的字母公式是________.
【分析】直接用字母表示出计算公式即可。
26.用塑料绳捆扎一个圆柱形的蛋糕盒(如图),打结处正好是底面圆心,打结用去绳长10厘米.
(1)扎这个盒子至少用去塑料绳多少厘米?
(2)在它的整个侧面贴上商标和说明,这部分的面积至少多少平方厘米?
四.解答题
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
四.解答题
【答案】 (1)解:20×4+40×4+10
=80+160+10
=250(厘米)
答:扎这个盒子至少用去塑料绳250厘米。
(2)解:面积:3.14×40×20
=125.6×20
=2512(平方厘米)
答:在它的整个侧面贴上商标和说明,这部分的面积是2512平方厘米。
【解析】【分析】(1)扎这个盒子至少用去塑料绳的长度=蛋糕的直径×4+蛋糕的高×4+打结处的长度;
(2)侧面贴上商标和说明这部分的面积=蛋糕的侧面积=蛋糕的底面周长×蛋糕的高,其中蛋糕的底面周长=蛋糕的底面直径×π。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
27.计算下面图形的体积。
四.解答题
【答案】 解:3.14×(6÷2)2×4+×3.14×(6÷2)2×6
=113.04+56.52
=169.56(dm3)
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
【解析】【分析】由图可知此图形的体积为圆锥的体积与圆柱的体积之和,圆锥的体积公式为: V= πr h ,圆柱的体积公式为:V=πr h ,假设圆锥的高为h,圆柱的高为H,半径为直径的一半,则此图形的体积为:V= πr h+πr H,将数值代入计算即可。
28.求解图中花布的面积。
四.解答题
【答案】解:由题意可知,所求花布的面积实际是求该圆柱5cm高的侧面积,
侧面展开图中,长方形的长即底面周长为:πd=6×3.14=18.84(cm)
长方形的宽即花布所围成圆柱的高为:5cm
则花布的面积为:S=Ch=18.84×5=94.2(cm2)
【分析】根据图意可知,要求花布的面积,就是求高5cm的圆柱的侧面积,先求出圆柱的底面周长,用公式:C=πd,然后用圆柱侧面积公式:S=Ch,据此列式解答.
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
29.把底面半径是6厘米、长是6厘米的圆柱形木料做成一个最大的圆锥,应削去木料多少立方厘米?
四.解答题
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
【答案】解:3.14×6 ×6× =452.16(立方厘米)
答:应削去木料452.16立方厘米。
【分析】把一个圆柱形木料做成一个最大的圆锥(说明同底、等高),圆柱变圆锥,体积就减少到圆柱体积的 ,把圆柱体积看作单位“1”,减少了圆柱体积的(1- );圆柱的底面半径和高都已知,体积可求,体积的(1- )是多少,据此可求削去木料的体积。
30.一个圆锥形沙堆,底面半径是10米,高是3米,这堆沙子有多少立方米?(写出用“分析法”分析问题、解决问题的过程.)
四.解答题
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
【答案】解:要求这堆沙子有多少立方米,即求圆锥形沙堆的体积,我们知道圆锥的体积公式:v= πr2h,直接运用圆锥体的体积解答; ×3.14×102×3
=3.14×100
=314(立方米)
答:这堆沙子有314立方米.
【解析】【分析】要求这堆沙子有多少立方米,即求圆锥形沙堆的体积,我们知道圆锥的体积公式:v= πr2h,直接运用圆锥体的体积计算公式解答即可.
31.只列综合算式(或方程),不计算。
(1)滨海大楼是一座28层的商住两用大楼,一至五层为办公区,平均层高4.5米;五层以上为住宅区,平均层高3米。这栋大楼的总高度是多少米?
(2)小红看一本课外书,计划每天看18页,15天看完;实际提前5天看完这本书,实际平均每天看多少页?
(3)一个直角三角形(如下图)以长直角边为轴,旋转一周形成了一个圆锥。这个圆锥的体积是多少立方厘米?
四.解答题
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
四.解答题
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
【答案】 (1)解:4.5×5+3×(28-5)
(2)解:18×15÷(15-5)
(3)解:3.14×42×5×
【分析】(1)根据题意可知,用五层以下的平均层高×5+五层以上的平均层高×(28-5)=这栋大楼的总高度,据此列式解答;
(2)此题主要考查了归总应用题,根据题意,用计划每天看的页数×计划看的天数÷实际看的天数=实际每天看的页数,据此列式解答;
(3) 一个直角三角形(如下图)以长直角边为轴,旋转一周形成了一个圆锥,则短直角边为圆锥的底面半径,长直角边为圆锥的高,用公式:V= πr2h,据此列式解答。
谢谢您的观看!
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
人教版六年级数学下册第三章
《圆柱与圆锥》知识讲解及考前押题卷精讲
(第四套)
专题复习课件
知识讲解
01
第一部分 知识讲解
一、圆柱
1、圆柱的形成:圆柱是以长方形的一边为轴旋转而得到的。
圆柱也可以由长方形卷曲而得到。(两种方式:1.以长方形的长为底面周长,宽为高;2.以长方形的宽为底面周长,长为高。其中,第一种方式得到的圆柱体体积较大。)
2、圆柱的高是两个底面之间的距离,一个圆柱有无数条高,他们的数值是相等的
3、圆柱的特征:
(1)底面的特征:圆柱的底面是完全相等的两个圆。
(2)侧面的特征:圆柱的侧面是一个曲面。
(3)高的特征 :圆柱有无数条高
4、圆柱的切割:①横切:切面是圆,表面积增加2倍底面积,即S 增 =2πr2
②竖切(过直径):切面是长方形(如果h=2R,切面为正方形),该长方形的长是圆柱的高,宽是圆柱的底面直径,表面积增加两个长方形的面积,即S增=4rh
第一部分 知识讲解
5、圆柱的侧面展开图:①沿着高展开,展开图形是长方形,如果h=2πr,展开图形为正方形
②不沿着高展开,展开图形是平行四边形或不规则图形
③无论怎么展开都得不到梯形
6、圆柱的相关计算公式:底面积 :S底=πr2
底面周长:C底=πd=2πr
侧面积 :S侧=2πrh
表面积 :S表=2S底+S侧=2πr2+2πrh
体积 :V柱=πr2h
考试常见题型:①已知圆柱的底面积和高, 求圆柱的侧面积,表面积,体积,底面周长
②已知圆柱的底面周长和高,求圆柱的侧面积,表面积,体积,底面积
③已知圆柱的底面周长和体积,求圆柱的侧面积,表面积,高,底面积
④已知圆柱的底面面积和高,求圆柱的侧面积,表面积,体积
第一部分 知识讲解
⑤已知圆柱的侧面积和高, 求圆柱的底面半径,表面积,体积,底面积
以上几种常见题型的解题方法,通常是求出圆柱的底面半径和高,再根据圆柱的相关计算公式进行计算
无盖水桶的表面积 =侧面积+一个底面积
油桶的表面积=侧面积+两个底面积
烟囱通风管的表面积=侧面积
只求侧面积:灯罩、排水管、漆柱、通风管、压路机、卫生纸中轴、薯片盒包装
侧面积+一个底面积:玻璃杯、水桶、笔筒、帽子、游泳池
侧面积+两个底面积:油桶、米桶、罐桶类
二、圆锥
1、圆柱的形成:圆锥是以直角三角形的一直角边为轴旋转而得到的
圆锥也可以由扇形卷曲而得到
第一部分 知识讲解
第一部分 知识讲解
2、圆锥的高是两个顶点与底面之间的距离,与圆柱不同,圆锥只有一条高
3、圆锥的特征:
(1)底面的特征:圆锥的底面一个圆。
(2)侧面的特征:圆锥的侧面是一个曲面。
(3)高的特征 :圆锥有一条高。
4、圆柱的切割:①横切:切面是圆
②竖切(过顶点和直径直径):切面是等腰三角形,该等腰三角形的高是圆锥的高,底是圆锥的底面直径,面积增加两个等腰三角形的面积,即S增=2rh
5、圆锥的相关计算公式:底面积 :S底=πr2
底面周长:C底=πd=2πr
体积:V锥= πr2h
考试常见题型:①已知圆锥的底面积和高,求体积,底面周长
第一部分 知识讲解
②已知圆锥的底面周长和高,求圆锥的体积,底面积
③已知圆锥的底面周长和体积,求圆锥的高,底面积
以上几种常见题型的解题方法,通常是求出圆锥的底面半径和高,再根据圆柱的相关计算公式进行计算。
1、圆柱与圆锥等底等高,圆柱的体积是圆锥的3倍。
2、圆柱与圆锥等底等体积,圆锥的高是圆柱的3倍。
3、圆柱与圆锥等高等体积,圆锥的底面积(注意:是底面积而不是底面半径)是圆柱的3倍。
4、圆柱与圆锥等底等高 ,体积相差 Sh
题型总结
①直接利用公式:分析清楚求的的是表面积,侧面积、底面积、体积
分析清楚半径变化导致底面周长、侧面积、底面积、体积的变化
分析清楚两个圆柱(或两个圆锥)半径、底面积、底面周长、侧面积、表面积、体积之比
第一部分 知识讲解
②圆柱与圆锥关系的转换:包括削成最大体积的问题(正方体,长方体与圆柱圆锥之间)
③横截面的问题
④浸水体积问题:(水面上升部分的体积就是浸入水中物品的体积,等于盛水容积的底面积乘以上升的高度)容积是圆柱或长方体,正方体
⑤等体积转换问题:一个圆柱融化后做成圆锥,或圆柱中的溶液倒入圆锥,都是体积不变的 问题,注意不要乘以
考前押题卷精讲
(全解析)
02
第二部分 学习检测
05
讲解脉络
01
02
03
04
选择题
判断题
填空题
解答题
一.单选题
1.圆柱体,上下两个面是( )
A. 长方形 B. 正方形 C. 圆 D. 三角形
C
【答案】C
【分析】根据圆柱的概念来判断。圆柱是由两个大小相等、相互平行的圆形(底面)以及连接两个底面的一个曲面(侧面)围成的几何体
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
2.把一个圆柱的侧面展开,不可能得到下面的图形是( )
A. B. C. D.
一.单选题
C
【解析】【解答】圆柱的侧面沿高展开是长方形或正方形,如果沿斜线展开得到的图形是一个平行四边形,侧面无论怎样展开绝对不是三角形。
【分析】根据圆柱的特征,圆柱的侧面是一个曲面,侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高,特殊情况当圆柱的底面周长和高相等时,侧面沿高展开是一个正方形,如果沿斜线展开,得到的是一个平行四边形.侧面无论怎样展开绝对不是三角形.由此解答。
故选:C。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
3.一个圆柱体,侧面展开后得到一个正方形,它的高是底面半径的( )倍.
A. 2 B. 2π C. π
一.单选题
B
【解析】【解答】 一个圆柱体,侧面展开后得到一个正方形,它的高是底面半径的:2πr÷r=2π倍.
故答案为:B.
【分析】一个圆柱体,侧面展开后得到一个正方形,它的高与底面周长相等,圆柱的底面周长C=2πr,也就是高是2πr,然后用圆柱的高÷底面半径=倍数,据此列式解答.
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
4.求一个圆柱形水桶能盛多少水,就是求这个水桶的( )。
A. 侧面积 B. 表面积 C. 容积
一.单选题
C
【解析】【解答】解:求一个圆柱形水桶能盛多少水,就是求这个水桶的容积。
故答案为:C。
【分析】容积是物体所能容纳物体的体积,由此判断并选择即可。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
5.右图中,大圆锥的底面半径是小圆锥的2倍,高也是小圆锥的2倍,大圆
锥的体积是小圆锥的( )倍。
A.2 B.4 C.6 D.8
一.单选题
D
【解析】【解答】2x2x2=8
故答案为:D
【分析】从题中条件可知,大圆锥的底面半径是小圆锥的2倍,那么,大圆锥的底面积就是小圆锥底面积的4倍,圆锥的体积=底面积x高x1/3 , 圆锥体积的大小跟圆锥底面积和高有关。因此,大圆锥体积是小圆锥体积的8倍。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
6.在下面的图形中,以直线为轴旋转,可以得到圆锥的是( )。
A. B. C. D.
一.单选题
C
【解析】【解答】 在下面的图形中,以直线为轴旋转,可以得到圆锥的是 .
故答案为:C.
【分析】一个直角三角形以一条直角边为轴,旋转一周,得到的图形是圆锥,据此解答.
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
一.单选题
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
7.一个圆柱与一个圆锥的体积和底面积都相等,圆柱的高是圆锥的( )。
A. 2倍 B. C. 3倍 D.
B
【解析】【解答】 一个圆柱与一个圆锥的体积和底面积都相等,圆柱的高是圆锥的 倍。 故答案为:B。
【分析】 圆柱的体积公式为: V=Sh,圆柱的体积公式为: V= Sh,根据圆柱与圆锥体积的关系:等底等高的圆柱和圆锥,圆柱的体积是圆锥的3倍,圆锥的体积是圆柱的 , 推出圆柱与圆锥的底面积关系为:圆柱的高是圆锥的 倍,由此可得出答案。
8.圆柱的底面半径扩大到原来的2倍,高也扩大到原来的2倍,体积( )
A. 扩大到原来的4倍 B. 不变 C. 扩大到原来的8倍 D. 不能确定
一.单选题
C
【解析】【解答】 圆柱的底面半径扩大到原来的2倍,高也扩大到原来的2倍,体积扩大到原来的8倍。
故答案为:C。
【分析】圆柱的体积公式:V=πr2h,圆柱的底面半径扩大到原来的a倍,高也扩大到原来的a倍,体积扩大到原来的a3倍。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
9.把一根长1米,底面积为3.14平方米的圆柱锯成两个小圆柱,它的表面积( )
A. 增加3.14平方米 B. 减少3.14平方米
C. 增加6.28平方米 D. 减少6.28平方米
一.单选题
C
【解析】【解答】切割后表面积增加了:3.14×2=6.28(平方米)
【分析】把圆柱切割成2个小圆柱后,表面积增加了2个圆柱的底面积,由此即可解答。
故选:C
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
10.一个圆柱和一个圆锥,底面周长的比是2:3,体积比是5:6,那么这个圆柱和圆锥高的最简单的整数比是( )
A. 8:5 B. 5:8 C. 12:5 D. 5:12
一.单选题
B
【解析】【解答】解:底面半径的比也是2:3。高的比:
故答案为:B。
【分析】底面周长的比与底面半径的比相等,把圆柱的底面半径看作2,体积看作5,圆锥的底面半径看作3,体积看作6;根据体积公式分别表示出圆柱的高和圆锥的高,然后写出高的最简整数比即可。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
11.圆柱和圆锥都有无数条高。 ( )
二.判断题
错误
【解析】【解答】圆柱有无数条高,圆锥只有一条高,原题说法错误.
故答案为:错误.
【分析】根据圆柱和圆锥高的定义:圆柱的上、下底面之间的距离叫做圆柱的高,圆柱的高有无数条;从圆锥的顶点到底面圆心的距离叫做圆锥的高,圆锥只有1条高,据此判断.
12.一个圆锥的侧面展开图是一个三角形。 ( )
【解析】【解答】解:一个圆锥的侧面展开图是一个扇形,原题说法错误.
故答案为:错误
【分析】圆锥是由一个圆形的底面和一个曲面组成的,曲面展开后是一个扇形.
错误
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
13.圆锥的体积一定等于圆柱的 1/3 。 ( )
二.判断题
错误
【答案】 错误
【分析】这里没有指出圆锥与圆柱的底与高。
14.一个圆柱的直径和高相等,则圆柱体的侧面展开图是正方形。 ( )
【解答】解:设一个圆柱的直径为d厘米,高也为d厘米。
底面周长=d ;因d >d,故侧面展开图不是正方形。
故答案为:错误。
【分析】如果一个圆柱的底面周长和高相等,那么圆柱体的侧面展开图就是正方形。
错误
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
15.一张长方形铁皮分别横着、竖着卷成两个圆柱,把它们竖放在桌面上,它们的容积完全相同。( )
二.判断题
错误
【解析】【解答】解: 一张长方形铁皮分别横着、竖着卷成两个圆柱,把它们竖放在桌面上,它们的容积不相同。原题说法错误。
故答案为:错误。
【分析】卷成的两个圆柱的底面积和高都不同,不能确定他们的容积是相等的。只能说它们的侧面积相等。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
16.圆柱的上、下底面是两个面积相等的________形.圆柱的侧面是一个________,沿着高展开后可能是一个________形,也可能是一个________形.
三.填空题
长方
【解析】【解答】解:圆柱的上、下底面是两个面积相等的圆形,圆柱的侧面是一个曲面,沿着高展开后可能是一个长方形,也可能是一个正方形。
故答案为:圆;曲面;长方;正方。
【分析】圆柱的两个底面是圆形,侧面是一个曲面,侧面沿着高展开后是一个长方形或正方形,圆柱的底面周长与高相等,侧面展开就是一个正方形。
圆
曲面
正方
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
17.________绕它的一条边旋转一周可以形成圆柱,直角三角形绕它的一条直角边旋转一周可以形成________.
三.填空题
长方形
【解析】【解答】 长方形绕它的一条边旋转一周可以形成圆柱,直角三角形绕它的一条直角边旋转一周可以形成圆锥.
故答案为:长方形;圆锥.
【分析】长方形绕长或宽为轴旋转一周可以形成圆柱,直角三角形绕它的一条直角边旋转一周可以形成圆锥,据此解答.
圆锥
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
18.圆锥的底面是个________形,从圆锥的顶点到底面圆心的距离叫做圆锥的________。
三.填空题
圆
【解析】【解答】解:圆锥的底面是个圆形,从圆锥的顶点到底面圆心的距离叫做圆锥的高。
故答案为:圆;高。
【分析】根据圆锥的特征作答即可。
高
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
19.一个圆柱和一个圆锥等底等高,圆柱与圆锥的体积之和是60立方厘米,圆柱的体积是________立方厘米,圆锥的体积是________立方厘米。
三.填空题
45
15
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
【解析】【解答】圆柱的体积:
60÷(1+ )
=60÷
=60×
=45(立方厘米);
圆锥的体积:45× =15(立方厘米).
故答案为:45;15.
【分析】根据题意可知,等底等高的圆锥体积是圆柱体积的 , 把圆柱的体积看作单位“1”,则圆锥的体积是 , 用圆柱和圆锥的体积之和÷(1+ )=圆柱的体积,然后用圆柱的体积× =圆锥的体积,据此列式解答.
20.计算下列圆柱的表面积.
表面积是________
三.填空题
182.12
【解析】【解答】3.14×(4÷2) ×2+3.14×4×12.5
=25.12+157
=182.12(平方分米)
故答案为:182.12
【分析】根据圆面积公式计算底面积,用底面周长乘高求出圆柱的侧面积,用侧面积加上底面积的2倍即可求出表面积.
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
21.一个底面直径和高都是3分米的圆锥,它的体积是________立方分米,一个与它等底等高的圆柱的体积比它大________立方分米.
三.填空题
7.065
14.13
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
【解析】【解答】解: x 3.14× ×3,
= ×3.14× ×3,
=7.065(立方分米),
7.065×2=14.13(立方分米),
答:它的体积是7.065立方分米,一个与它等底等高的圆柱的体积比它大 14.13立方分米.
故答案为:7.065;14.13.
【分析】(1)利用圆锥的体积= πr2×h,代入数据即可解决问题;(2)等底等高的圆柱的体积是圆锥的体积的3倍,所以与它等底等高的圆柱就比这个圆锥大了它的2倍,由此即可解决问题.
22.一根1米长的圆柱体钢材,截去2分米的一段后,表面积减少25.12平方分米,原来这根钢材的体积是________立方分米.
三.填空题
125.6
【解析】【解答】1米=10分米;25.12÷2÷3.14÷2=2(分米);3.14×2 ×10=125.6(立方分米)。
故答案为:125.6.
【分析】25.12是长为2分米的圆柱的侧面积;侧面积÷长=底面周长;底面周长÷π÷2=底面半径;π×底面半径的平方×高=圆柱体积。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
23.一个正方体木块的棱长是6dm , 把它削成一个最大的圆柱体,圆柱体的体积是________dm3 , 再把这个圆柱体削成一个最大的圆锥体,圆锥体的体积是________dm3 .
三.填空题
169.56
【解析】【解答】6÷2=3(dm)
3.14×32×6
=3.14×9×6
=169.56(dm3)
169.56× =56.52(dm3)
故答案为:169.56;56.52。
【分析】将一个正方体木块削成一个最大的圆柱体,圆柱体的底面直径和高是正方体的棱长,要求圆柱的体积,用公式:V=πr2h,据此列式解答;
把一个圆柱体削成一个最大的圆锥体,圆锥的体积是等底等高的圆柱体积的1/3, 据此列式解答。
56.52
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
三.填空题
25.施灵为了测量萝卜的体积,先将一个萝卜削成一个长5厘米、宽4厘米、高2厘米的长方体,并用天平称出这个长方体重20克.接着用天平称出要测量体积的萝卜重320克.这个萝卜的体积是________立方厘米?
【解析】【解答】320÷[20÷(5×4×2)]
=320÷[20÷40]
=320÷0.5
=640(立方厘米)
【分析】先根据长方体的体积公式V=abh,求出长方体萝卜的体积,即5×4×2=40立方厘米,用20除以40,求出1立方厘米重多少克,再用320除以1立方厘米萝卜的重量,即可求出这个萝卜的体积是多少立方厘米,列式解答即可。
640
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
【解析】【解答】圆锥的体积公式用字母表示:V= Sh .
故答案为:V= Sh。
24.计算圆锥体积的字母公式是________.
【分析】直接用字母表示出计算公式即可。
26.用塑料绳捆扎一个圆柱形的蛋糕盒(如图),打结处正好是底面圆心,打结用去绳长10厘米.
(1)扎这个盒子至少用去塑料绳多少厘米?
(2)在它的整个侧面贴上商标和说明,这部分的面积至少多少平方厘米?
四.解答题
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
四.解答题
【答案】 (1)解:20×4+40×4+10
=80+160+10
=250(厘米)
答:扎这个盒子至少用去塑料绳250厘米。
(2)解:面积:3.14×40×20
=125.6×20
=2512(平方厘米)
答:在它的整个侧面贴上商标和说明,这部分的面积是2512平方厘米。
【解析】【分析】(1)扎这个盒子至少用去塑料绳的长度=蛋糕的直径×4+蛋糕的高×4+打结处的长度;
(2)侧面贴上商标和说明这部分的面积=蛋糕的侧面积=蛋糕的底面周长×蛋糕的高,其中蛋糕的底面周长=蛋糕的底面直径×π。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
27.计算下面图形的体积。
四.解答题
【答案】 解:3.14×(6÷2)2×4+×3.14×(6÷2)2×6
=113.04+56.52
=169.56(dm3)
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
【解析】【分析】由图可知此图形的体积为圆锥的体积与圆柱的体积之和,圆锥的体积公式为: V= πr h ,圆柱的体积公式为:V=πr h ,假设圆锥的高为h,圆柱的高为H,半径为直径的一半,则此图形的体积为:V= πr h+πr H,将数值代入计算即可。
28.求解图中花布的面积。
四.解答题
【答案】解:由题意可知,所求花布的面积实际是求该圆柱5cm高的侧面积,
侧面展开图中,长方形的长即底面周长为:πd=6×3.14=18.84(cm)
长方形的宽即花布所围成圆柱的高为:5cm
则花布的面积为:S=Ch=18.84×5=94.2(cm2)
【分析】根据图意可知,要求花布的面积,就是求高5cm的圆柱的侧面积,先求出圆柱的底面周长,用公式:C=πd,然后用圆柱侧面积公式:S=Ch,据此列式解答.
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
29.把底面半径是6厘米、长是6厘米的圆柱形木料做成一个最大的圆锥,应削去木料多少立方厘米?
四.解答题
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
【答案】解:3.14×6 ×6× =452.16(立方厘米)
答:应削去木料452.16立方厘米。
【分析】把一个圆柱形木料做成一个最大的圆锥(说明同底、等高),圆柱变圆锥,体积就减少到圆柱体积的 ,把圆柱体积看作单位“1”,减少了圆柱体积的(1- );圆柱的底面半径和高都已知,体积可求,体积的(1- )是多少,据此可求削去木料的体积。
30.一个圆锥形沙堆,底面半径是10米,高是3米,这堆沙子有多少立方米?(写出用“分析法”分析问题、解决问题的过程.)
四.解答题
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
【答案】解:要求这堆沙子有多少立方米,即求圆锥形沙堆的体积,我们知道圆锥的体积公式:v= πr2h,直接运用圆锥体的体积解答; ×3.14×102×3
=3.14×100
=314(立方米)
答:这堆沙子有314立方米.
【解析】【分析】要求这堆沙子有多少立方米,即求圆锥形沙堆的体积,我们知道圆锥的体积公式:v= πr2h,直接运用圆锥体的体积计算公式解答即可.
31.只列综合算式(或方程),不计算。
(1)滨海大楼是一座28层的商住两用大楼,一至五层为办公区,平均层高4.5米;五层以上为住宅区,平均层高3米。这栋大楼的总高度是多少米?
(2)小红看一本课外书,计划每天看18页,15天看完;实际提前5天看完这本书,实际平均每天看多少页?
(3)一个直角三角形(如下图)以长直角边为轴,旋转一周形成了一个圆锥。这个圆锥的体积是多少立方厘米?
四.解答题
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
四.解答题
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第四套)
【答案】 (1)解:4.5×5+3×(28-5)
(2)解:18×15÷(15-5)
(3)解:3.14×42×5×
【分析】(1)根据题意可知,用五层以下的平均层高×5+五层以上的平均层高×(28-5)=这栋大楼的总高度,据此列式解答;
(2)此题主要考查了归总应用题,根据题意,用计划每天看的页数×计划看的天数÷实际看的天数=实际每天看的页数,据此列式解答;
(3) 一个直角三角形(如下图)以长直角边为轴,旋转一周形成了一个圆锥,则短直角边为圆锥的底面半径,长直角边为圆锥的高,用公式:V= πr2h,据此列式解答。
谢谢您的观看!
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
