湖南省凤凰县华鑫中学2011-2012学年高二2月月考数学(文)试题
文档属性
| 名称 | 湖南省凤凰县华鑫中学2011-2012学年高二2月月考数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 322.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-08 15:23:06 | ||
图片预览



文档简介
试卷满分:150分 考试时间:120分钟 出卷人:周伟
一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,,则=( )
A. B. C. D.
2. 已知命题、,如果是的充分而不必要条件,那么是的( )
A.必要不充分条件 B.充分不必要条件 C.要条件 D.不充分也不必要
3.下列函数中,值域是的函数是( )
A B C D
4. 下列说法不正确的是( )
空间中,一组对边平行且相等的四边形是一定是平行四边形;
B.同一平面的两条垂线一定共面;
C. 过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内;
D. 过一条直线有且只有一个平面与已知平面垂直.
5. 有一个几何体的三视图及其尺寸如下(单位),则该几何体的表面积及
体积为( ).
A., B. ,
C. , D. 以上都不正确
6. 中心点在原点,准线方程为,离心率为的椭圆方程是( )
A. B. C. D.
7. 如果方程表示双曲线,那么实数的取值范围是( )
A. B.或 C. D.或
8.若,当时,,若在区间内,有两个零点,则实数m的取值范围是 ( )
A. B. C. D.
二、填空题:本大题共7小题,每小题5分,共35分.
9. 复数的共轭复数是 。
10. 已知与,若两直线平行,则的值为 .
11. 求函数的定义域 __________
12. 前10项的和为____________
13.函数,,则函数的最小值是 ;
14.已知实数x、y满足的最小值等于 。
15. 设,则f(x)+f(1-x)=______,并利用推导等差数列前n项和公式的方法,求得f(-5)+f(-4)+···+f(0)+···+f(5)+f(6)的值为_________
三.解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演示步骤.
16.(本小题满分12分)
已知函数
(1)求函数的最大值和最小正周期;
(2)设的内角的对边分别且,,若求的值.
17. (本小题满分12分)
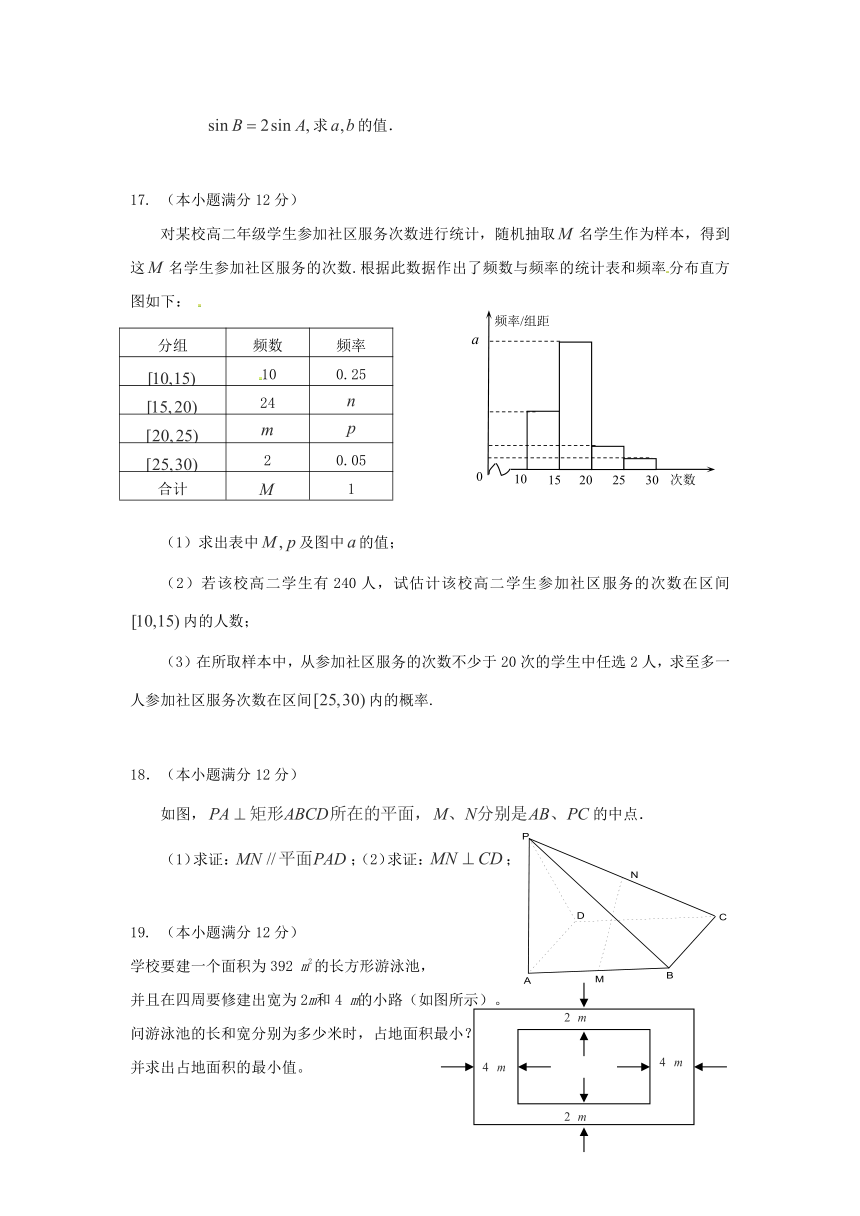
对某校高二年级学生参加社区服务次数进行统计,随机抽取名学生作为样本,得到这名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 频数 频率
10 0.25
24
2 0.05
合计 1
(1)求出表中及图中的值;
(2)若该校高二学生有240人,试估计该校高二学生参加社区服务的次数在区间内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间内的概率.
18.(本小题满分12分)
如图,的中点.
(1)求证:;(2)求证:;
19. (本小题满分12分)
学校要建一个面积为392 m2的长方形游泳池,
并且在四周要修建出宽为2m和4 m的小路(如图所示)。
问游泳池的长和宽分别为多少米时,占地面积最小?
并求出占地面积的最小值。
20.(本小题满分13分)
P为椭圆上任意一点,为左、右焦点,如图所示.
(1)若的中点为,求证:
(2)若∠,求|PF1|·|PF2|之值;
(3)椭圆上是否存在点P,使·=0,若存在,
求出P点的坐标,若不存在,试说明理由
21.(本小题满分14分)
设函数.(1)求函数的最小值;
(2)设,讨论函数的单调性;
(3)斜率为的直线与曲线交于、两点,
求证:
凤凰县华鑫中学2011-2012学年高二下(2月)月考物理试题高二数学(文科) 参考答案
17. (本小题满分12分)
【解析】(1)由分组内的频数是,频率是知,,
所以.
因为频数之和为,所以,.
.
因为是对应分组的频率与组距的商,所以. ……(4分)
18. (本小题满分12分)
证明:(1)取为中点,
19. (本小题满分12分)
解:设游泳池的长为x m,则游泳池的宽为m,
又设占地面积为y m2,依题意,
得=424+4(x+)≥424+224=648
当且仅当x=即x=28时取“=”.
答:游泳池的长为28 m宽为m时,占地面积最小为648 m2。
20. (本小题满分12分)
【解析】(1)证明:在△F1PF2中,MO为中位线,
∴|MO|===a-=5-|PF1|.
(2)解:∵ |PF1|+|PF2|=10,
∴|PF1|2+|PF2|2=100-2|PF1|·|PF2|,
在△PF1F2中,cos 60°=,
∴|PF1|·|PF2|=100-2|PF1|·|PF2|-36,∴|PF1|·|PF2|=.
(3)设点P(x0,y0),则+=1.①
易知F1(-3,0),F2(3,0),故PF1=(-3-x0,-y0),
PF2=(-3-x0,-y0),
∵PF1·PF2=0,∴x-9+y=0,②
由①②组成方程组,此方程组无解,故这样的点P不存在.
21.(本小题满分14分)
要证,即证,等价于证,令,
则只要证,由知,故等价于证 (*).
① 设,则,故在上是增函数,
∴ 当时,,即.
② 设,则,故在上是增函数,
∴ 当时,,即.
由①②知(*)成立,得证.
6
5
频率/组距
15
25
20
10
0
30
次数
a
一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,,则=( )
A. B. C. D.
2. 已知命题、,如果是的充分而不必要条件,那么是的( )
A.必要不充分条件 B.充分不必要条件 C.要条件 D.不充分也不必要
3.下列函数中,值域是的函数是( )
A B C D
4. 下列说法不正确的是( )
空间中,一组对边平行且相等的四边形是一定是平行四边形;
B.同一平面的两条垂线一定共面;
C. 过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内;
D. 过一条直线有且只有一个平面与已知平面垂直.
5. 有一个几何体的三视图及其尺寸如下(单位),则该几何体的表面积及
体积为( ).
A., B. ,
C. , D. 以上都不正确
6. 中心点在原点,准线方程为,离心率为的椭圆方程是( )
A. B. C. D.
7. 如果方程表示双曲线,那么实数的取值范围是( )
A. B.或 C. D.或
8.若,当时,,若在区间内,有两个零点,则实数m的取值范围是 ( )
A. B. C. D.
二、填空题:本大题共7小题,每小题5分,共35分.
9. 复数的共轭复数是 。
10. 已知与,若两直线平行,则的值为 .
11. 求函数的定义域 __________
12. 前10项的和为____________
13.函数,,则函数的最小值是 ;
14.已知实数x、y满足的最小值等于 。
15. 设,则f(x)+f(1-x)=______,并利用推导等差数列前n项和公式的方法,求得f(-5)+f(-4)+···+f(0)+···+f(5)+f(6)的值为_________
三.解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演示步骤.
16.(本小题满分12分)
已知函数
(1)求函数的最大值和最小正周期;
(2)设的内角的对边分别且,,若求的值.
17. (本小题满分12分)
对某校高二年级学生参加社区服务次数进行统计,随机抽取名学生作为样本,得到这名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 频数 频率
10 0.25
24
2 0.05
合计 1
(1)求出表中及图中的值;
(2)若该校高二学生有240人,试估计该校高二学生参加社区服务的次数在区间内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间内的概率.
18.(本小题满分12分)
如图,的中点.
(1)求证:;(2)求证:;
19. (本小题满分12分)
学校要建一个面积为392 m2的长方形游泳池,
并且在四周要修建出宽为2m和4 m的小路(如图所示)。
问游泳池的长和宽分别为多少米时,占地面积最小?
并求出占地面积的最小值。
20.(本小题满分13分)
P为椭圆上任意一点,为左、右焦点,如图所示.
(1)若的中点为,求证:
(2)若∠,求|PF1|·|PF2|之值;
(3)椭圆上是否存在点P,使·=0,若存在,
求出P点的坐标,若不存在,试说明理由
21.(本小题满分14分)
设函数.(1)求函数的最小值;
(2)设,讨论函数的单调性;
(3)斜率为的直线与曲线交于、两点,
求证:
凤凰县华鑫中学2011-2012学年高二下(2月)月考物理试题高二数学(文科) 参考答案
17. (本小题满分12分)
【解析】(1)由分组内的频数是,频率是知,,
所以.
因为频数之和为,所以,.
.
因为是对应分组的频率与组距的商,所以. ……(4分)
18. (本小题满分12分)
证明:(1)取为中点,
19. (本小题满分12分)
解:设游泳池的长为x m,则游泳池的宽为m,
又设占地面积为y m2,依题意,
得=424+4(x+)≥424+224=648
当且仅当x=即x=28时取“=”.
答:游泳池的长为28 m宽为m时,占地面积最小为648 m2。
20. (本小题满分12分)
【解析】(1)证明:在△F1PF2中,MO为中位线,
∴|MO|===a-=5-|PF1|.
(2)解:∵ |PF1|+|PF2|=10,
∴|PF1|2+|PF2|2=100-2|PF1|·|PF2|,
在△PF1F2中,cos 60°=,
∴|PF1|·|PF2|=100-2|PF1|·|PF2|-36,∴|PF1|·|PF2|=.
(3)设点P(x0,y0),则+=1.①
易知F1(-3,0),F2(3,0),故PF1=(-3-x0,-y0),
PF2=(-3-x0,-y0),
∵PF1·PF2=0,∴x-9+y=0,②
由①②组成方程组,此方程组无解,故这样的点P不存在.
21.(本小题满分14分)
要证,即证,等价于证,令,
则只要证,由知,故等价于证 (*).
① 设,则,故在上是增函数,
∴ 当时,,即.
② 设,则,故在上是增函数,
∴ 当时,,即.
由①②知(*)成立,得证.
6
5
频率/组距
15
25
20
10
0
30
次数
a
同课章节目录
