人教高中物理必修二5.2.2运动的合成与分解 课件(60张ppt)
文档属性
| 名称 | 人教高中物理必修二5.2.2运动的合成与分解 课件(60张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-02 16:11:26 | ||
图片预览










文档简介
(共60张PPT)
运动的合成与分解
第二课时
1、定义:运动轨迹是曲线的运动
曲线运动
2、运动方向:轨迹的切线方向
3、条件:
物体所受合外力方向与速度方向不在同一条直线上;
加速度方向与物体的速度方向不在同一条直线上;
4、轨迹特点:
轨迹在速度方向和合力方向之间,且向合力方向一侧弯曲
合力的效果:
合力沿切线方向的分力改变速度的大小,沿径向的分力改变速度的方向
P6活动:
三、运动的合成与分解
既然合运动与二分运动等效,则合位移与分位移的关系如何呢?
1、位移的合成与分解满足平行四边形定则
四、运动的合成分解规则
A
B
s
x1
x2
合位移
分位移
分位移
2、由合运动与分运动的等时性,速度的合成与分解亦遵循平行四边形定则。
3、已知分运动求合运动为运动的合成,反之则为运动的分解!
1、物体实际的运动叫合运动
2、物体同时参与合成的运动的运动叫分运动
3.由分运动求合运动的过程叫运动的合成
4.由合运动求分运动的过程叫运动的分解
几个概念
思考问题
提问:1、分运动和合运动有什么关系?(实验)
独立性、等时性、等效性
运动的独立性
一个物体同时参与几个分运动,各分运动独立进行,各自产生效果
运动的等效性
整体的合运动是各分运动决定的总效果,它替代所有的分运动
运动的等时性
合运动和分运动进行的时间相同
运动的矢量性
加速度、速度、位移都是矢量,合成和分解都遵循平行四边形定则
总结:
运动合成分解的四个性质
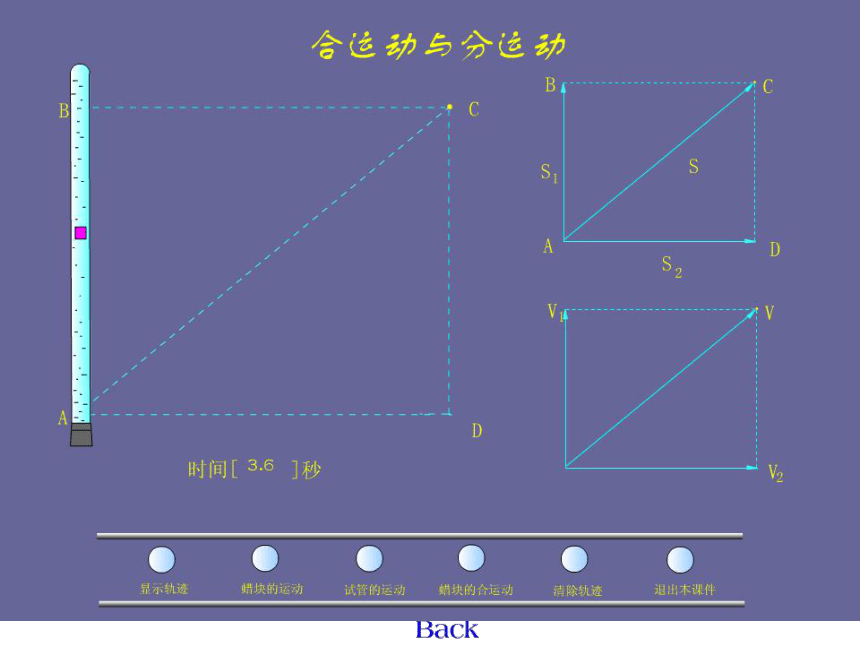
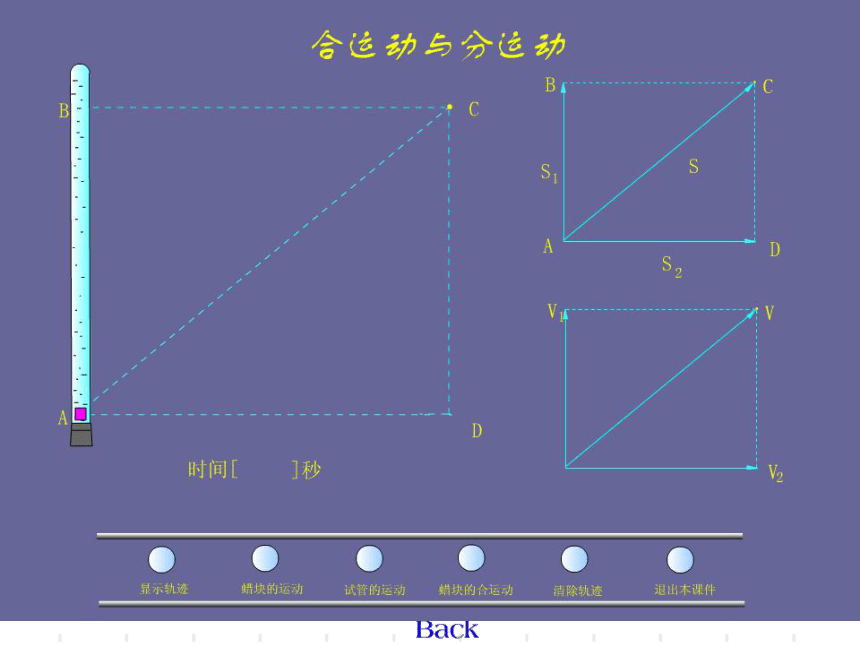
蜡块的运动
思考:蜡块的实际运动的轨迹是直线吗?实际运动是匀速运动吗?
蜡块既向上做匀速运动,又由于玻璃管的移动向右做匀速运动,即蜡块是向右上方运动的。
1.初速度为V0匀加速直线运动可以怎样分解?
怎样进行合成和分解:
初速度为V0匀加速直线运动可以看成是水平方向速度为V0的匀速运动和水平方向初速度为0的匀加速运动的合运动.即先取V0方向为正,则有:
V合=v0+at
s=v0t+
at2
a=0+a
竖直上抛运动可以看成是竖直方向的匀速运动和自由落体的合运动.即先取向上为正,则有:
vt=v0+(-gt)=v0-gt
s=v0t+(-
gt2)=v0t-
gt2
a=0+(-g)=-g
2、竖直上抛运动可以怎样分解?
几个特征
1.运动的独立性
2.运动的等时性
3.运动的等效性
4.运动的同一性
分析:蜡块的轨迹
O
x
y
P
蜡块的位置P
点的坐标
y
=
x
vx
vy
蜡块的运动轨迹是过原点的一条直线
y
=
vy
t
x
=
vx
t
O
x
y
P
θ
分析:蜡块的位移、速度
vy
vx
v
y
x
位移的大小:
位移的方向:
速度的大小:
运动的合成与分解
1、物体实际的运动叫合运动
2、物体同时参与合成的运动的运动叫分运动
3、由分运动求合运动的过程叫运动的合成
4、由合运动求分运动的过程叫运动的分解
红蜡块A
C
的匀速运动
A
B的匀速运动
A
D的匀速运动
(分运动)
(分运动)
(合运动)
A
R
C
D
B
两个分运动没有相互影响,是独立进行的
2.怎么知道蜡块的运动轨迹:
·
P
3.怎么知道蜡块的位移
上述过程怎么可以把本来发生的一个实际复杂运动,分解成了2个简单的运动,先分步求解,再合成求解?
4.怎么知道蜡块的速度
(大小,方向)
(大小,方向)
说明
1、运动的独立性
2、运动的等时性
3、运动的等效性
4、运动的同体性
a
a1
a2
v1
v2
v
运动的合成与分解是指
x、v、
a
的合成与分解。
速度、位移、加速度都是矢量,合成与分解时均遵循平行四边形定则
A
B
s
s1
s2
分速度
分速度
合速度
分加速度
合加速度
位移的合成
速度的合成
加速度的合成
分加速度
合位移
分位移
分位移
运动的合成是惟一的,而运动的分解不是惟一的,通常按运动所产生的实际效果分解。
运动的合成与分解
分运动的位置,位移,速度,加速度
合运动的位置,位移,速度,加速度
运动的合成
运动的分解
遵循平行四边形定则
独立,等时,等效
思考:上述蜡块的分运动均为匀速直线运动,那么所用的运动合成分解的思想方法在其他运动中是否还适用呢?
思考与讨论
如果物体在一个方向上的分运动是匀速直线运动,在与它垂直方向的分运动是匀加速运动,合运动的轨迹是什么样的?
P
x
=
vx
t
物体的位置P
的坐标
y
=
vy
t+
at2
1
2
y
=
x+
x2
vx
vy
2vx2
a
v
x
y
O
F合
vy
vx
1、分运动是匀速直线运动:
合运动是匀速直线运动
2、一个是匀速直线,一个是匀变速直线的合成:
合运动一定是匀变速曲线运动
3、两个都是是匀变速直线运动的合成:
(1)
若V合与a合(或F合)在一条直线上,则合运动为
直线运动。
(2)若V合与a合(或F合)不在一条直线上,则合运动
为曲线运动。
两个分运动合成时,合运动的形式:
4.合运动的性质与轨迹取决与a合与v合
的方向关系
(1)a合=0,合运动为匀速直线运动
(2)a合与v合在同一直线上,合运动为
加速或减速运动
(3)a合与v合不在同一直线上,合运动
为曲线运动
三、两直线运动的合运动的性质和轨迹
3.两个匀变速直线运动的合运动一定是
1.互成角度的两个匀速直线运动的合运动是
2.互成角度的一个匀速直线运动和一个匀变速直线运动的合运动是
⑴若合初速度方向与合加速度方向在同一条直线上时,则是
⑵若合初速度方向与合加速度方向不在同一条直线上时,则是
v
v1
v2
v
v1
v2
a1
v
v1
v2
a1
a2
a
v
v1
v2
a1
a2
a
匀速直线运动.
匀变速曲线运动.
匀变速运动.
匀变速直线运动.
(a合与v合共线)
匀变速曲线运动(a合与v合不共线).
结论
1、两个互成角度的匀速直线运动的合运动
匀速直线运动
2、两个互成角度的匀速直线运动与匀变速直线运动的合运动
匀变速曲线运动
a1
v1
a1
v1
思考与讨论
3、两个互成角度的匀变速直线运动的合运动
①两个初速度为0
的匀加速直线运动
判断几个分运动的合运动,可先把各分运动的合速度以及合加速度求出来,然后根据合速度与合加速度是否在一条直线上加以判断。
②两个初速度不为0
的匀变速直线运动
初速度为0的匀加速直线运动
匀变速直线运动
a2
v2
v
a2
v2
v
a
匀变速曲线运动
a
五、合运动性质的判定
1、两个互成角度的匀速直线运动的合运动?
2、互成角度的一个匀速直线运动和一个匀变速直线运动的合运动?
3、互成角度的两个匀变速直线运动的合运动?
一.运动的合成和分解
2.运动的合成和分解的方法
速度、位移、加速度的合成和分解——遵循平行四边形定则
1)合运动:物体实际的运动
2)分运动:与合运动等效的其它方向的运动
3)运动的合成:已知分运动求合运动
4)运动的分解:已知合运动求分运动
1.几个基本概念
x1
x2
x
v1
v2
v
a1
a2
a
x1
x2
x
3.合运动与分运动的关系
1)等效性:合运动的效果与各分运动共同产生的效果相同。
2)等时性:合运动与分运动所用时间相同。
3)独立性:各分运动各自按自己的规律运动,互不干扰。
合运动与分运动的区分原则:物体实际进行的运动一定是合运动,对应于平行四边形的对角线.
1)是直线运动还是曲线运动?(判断轨迹)
2)是匀变速运动还是变加速运动?(判断运动性质)
判断:不在一直线上的两个匀速直线运动的合运动?一个匀速直线运动与一个匀加速直线运动的合运动?两个匀变速直线运动的合运动?
思考:如何判断两个直线运动的合运动的运动轨迹和运动性质?
合力F合的方向或加速度a的方向与合速度v合的方向是否同一直线
合力或加速度是否恒定
v2
v
v2
v1
a1
a2
a
v1
v
a1
a2
a
加速直线运动
加速曲线运动
画图分析两个加速运动的合成
1、两互成角度的匀速直线运动的合成
(一定是匀速直线运动)
2、两互成角度的初速为零的匀加速直线运动的合成
(一定是匀加速直线运动)
3、两互成角度的初速不为零的匀加速直线运动的合成
(匀变速直线运动或匀变速曲线运动)
动的合成
(匀变速直线运动或匀变速曲线运动)
点评: 运动的合成
4、一个匀速直线运动和一个匀加速直线运
1、两个匀速直线
运动的合运动仍然是匀速直线运动
2、一个匀速直线运动与一个匀变速直线运动的合运动一定是曲线运动
3、两个初速度为零的匀变速直线运动合运动一定是初速度为零匀加速直线运动。合运动的方向即为合加速度的方向
4、两个初速度不为零的匀变速直线运动的合运动可能是匀变速直线运动,也可能是匀变速曲线运动
方法1.按运动的实际效果分解
方法2.正交分解
1)分解的原则
2)运动分解的典型问题
a.渡船问题的分解
b.拉绳问题的分解
4.运动的分解
合作学习:
讨论:
怎样判断两个直线运动的合运动的
轨迹是直线还是曲线?
友情提示:结合物体做曲线运动的条件!
直线运动
曲线运动
两个直线运动的合运动性质的讨论:
1、两个匀速直线运动的合运动——匀速直线运动
v1
v2
v
由两个分运动性质及合初速度与合加速度方向关系决定
2、一个匀速直线运动和一个匀变速直线运动的合运动
v0
a
v0
a
v0
g
v0
g
匀变速直线运动
v0
g
v0
g
匀变速曲线运动
3、两个匀变速直线运动的合运动
v0
v01
v02
a1
a2
a
v0
v01
v02
a1
a2
a
匀变速直线运动
匀变速曲线运动
1、两个匀速直线
运动的合运动仍然是匀速直线运动
2、一个匀速直线运动与一个匀变速直线运动的合运动一定是曲线运动
3、两个初速度为零的匀变速直线运动合运动一定是初速度为零匀加速直线运动。合运动的方向即为合加速度的方向
4、两个初速度不为零的匀变速直线运动的合运动可能是匀变速直线运动,也可能是匀变速曲线运动
合运动与分运动
【例1】关于互成角度的两个初速度不为0的匀变速直线运动的合运动,下述说法正确的是(
)
A.一定是直线运动
B.一定是抛物线运动
C.可能是直线运动,也可能是抛物线运动
D.以上说法都不对
c
小结
1、合运动与分运动的概念
3、运动的合成与分解遵循平行四边形定则
4、两个直线运动的合运动可能是直线运动,也可能是曲线运动
2、合运动与分运动的关系:独立性、等时性、等效性、同体性
运动的合成和分解的应用
———1.小船渡河
例1:一艘小船在100m宽的河中横渡到对岸,已知水流速度是3m/s,小船在静水中的速度是4m/s,求:(2)欲使船渡河时间最短,船应该怎样渡河?最短时间是多少?船经过的位移多大?
分析1:时间最短
d
结论:欲使船渡河时间最短,船头的方向应该垂直于河岸。
解1:当船头垂直河岸时,所用时间最短
最短时间
此时合速度
此时航程
例2:一艘小船在100m宽的河中横渡到对岸,已知水流速度是3m/s,小船在静水中的速度是4m/s,求:(1)欲使航行距离最短,船应该怎样渡河?渡河时间多长?
分析2:航程最短
θ
d
设船头指向与上游河岸成θ:
结论:当v船>v水时,最短航程等于河宽d。
解:2、当船头指向斜上游,与岸夹角为?时,合运动垂直河岸,航程最短,数值等于河宽100米。
过河时间:
合速度:
则cos
?
=
例3:若河宽仍为100m,已知水流速度是4m/s,小船在静水中的速度是3m/s,即船速(静水中)小于水速。
求:(1)欲使船渡河时间最短,船应该怎样渡河?
(2)欲使航行距离最短,船应该怎样渡河?最短航线是河宽吗?
θ
θ
结论:当v船<
v水时,最短航程不等于河宽d。
船头指向与上游河岸成θ:
【例题】如图所示,纤绳以恒定速率v沿水平方向通过定滑轮牵引小船靠岸,当纤绳与水面夹角为θ时,船靠岸的速度是
,若使船匀速靠岸,则纤绳的速度是
。(填:匀速、加速、减速)
【答案】
寻找分运动效果
减速
“绳+物”问题
【例题】如图所示,汽车沿水平路面以恒定速度v前进,则当拉绳与水平方向成θ角时,被吊起的物体M的速度为vM=
。
【答案】
寻找分运动效果
“绳+物”问题
【例题】如图所示,以速度v沿竖直杆匀速下滑的物体A,用细绳通过定滑轮拉动物体B在水平桌面上运动,当绳与水平面夹角为θ时,物体B的速率为
,
【答案】
vB=vsinθ
寻找分运动效果
“绳+物”问题
例:一条河宽500m,水流速度是3m/s,小船在静水中的速度是5m/s,求
(1)最短渡河的时间是多小?小船的实际位移,沿下流的位移是多少?
(2)最短位移渡河的时间是多少?最短渡河的位移是多少?
100s
【例题】一船准备渡河,已知水流速度为v2=1m/s,船在静水中的航速为v1=2m/s,则:
①要使船能够垂直地渡过河去,那么应向何方划船?
②要使船能在最短时间内渡河,应向何方划船?
平直的,洪水沿江向下游流去,水流速度为v1,摩托艇在静水中的航速为v2,战士救人的地点A离岸边最近处O的距离为d,如战士想在最短时间内将人送上岸,则摩托艇登陆的地点离O点的距离为(
)
A.dv2/
B.0
C.dv1/v2
D.dv2/v1
v22-
v12
C
【例题】.在抗洪抢险中,战士驾驶摩托艇救人,假设江岸是
运动的合成与分解
第二课时
1、定义:运动轨迹是曲线的运动
曲线运动
2、运动方向:轨迹的切线方向
3、条件:
物体所受合外力方向与速度方向不在同一条直线上;
加速度方向与物体的速度方向不在同一条直线上;
4、轨迹特点:
轨迹在速度方向和合力方向之间,且向合力方向一侧弯曲
合力的效果:
合力沿切线方向的分力改变速度的大小,沿径向的分力改变速度的方向
P6活动:
三、运动的合成与分解
既然合运动与二分运动等效,则合位移与分位移的关系如何呢?
1、位移的合成与分解满足平行四边形定则
四、运动的合成分解规则
A
B
s
x1
x2
合位移
分位移
分位移
2、由合运动与分运动的等时性,速度的合成与分解亦遵循平行四边形定则。
3、已知分运动求合运动为运动的合成,反之则为运动的分解!
1、物体实际的运动叫合运动
2、物体同时参与合成的运动的运动叫分运动
3.由分运动求合运动的过程叫运动的合成
4.由合运动求分运动的过程叫运动的分解
几个概念
思考问题
提问:1、分运动和合运动有什么关系?(实验)
独立性、等时性、等效性
运动的独立性
一个物体同时参与几个分运动,各分运动独立进行,各自产生效果
运动的等效性
整体的合运动是各分运动决定的总效果,它替代所有的分运动
运动的等时性
合运动和分运动进行的时间相同
运动的矢量性
加速度、速度、位移都是矢量,合成和分解都遵循平行四边形定则
总结:
运动合成分解的四个性质
蜡块的运动
思考:蜡块的实际运动的轨迹是直线吗?实际运动是匀速运动吗?
蜡块既向上做匀速运动,又由于玻璃管的移动向右做匀速运动,即蜡块是向右上方运动的。
1.初速度为V0匀加速直线运动可以怎样分解?
怎样进行合成和分解:
初速度为V0匀加速直线运动可以看成是水平方向速度为V0的匀速运动和水平方向初速度为0的匀加速运动的合运动.即先取V0方向为正,则有:
V合=v0+at
s=v0t+
at2
a=0+a
竖直上抛运动可以看成是竖直方向的匀速运动和自由落体的合运动.即先取向上为正,则有:
vt=v0+(-gt)=v0-gt
s=v0t+(-
gt2)=v0t-
gt2
a=0+(-g)=-g
2、竖直上抛运动可以怎样分解?
几个特征
1.运动的独立性
2.运动的等时性
3.运动的等效性
4.运动的同一性
分析:蜡块的轨迹
O
x
y
P
蜡块的位置P
点的坐标
y
=
x
vx
vy
蜡块的运动轨迹是过原点的一条直线
y
=
vy
t
x
=
vx
t
O
x
y
P
θ
分析:蜡块的位移、速度
vy
vx
v
y
x
位移的大小:
位移的方向:
速度的大小:
运动的合成与分解
1、物体实际的运动叫合运动
2、物体同时参与合成的运动的运动叫分运动
3、由分运动求合运动的过程叫运动的合成
4、由合运动求分运动的过程叫运动的分解
红蜡块A
C
的匀速运动
A
B的匀速运动
A
D的匀速运动
(分运动)
(分运动)
(合运动)
A
R
C
D
B
两个分运动没有相互影响,是独立进行的
2.怎么知道蜡块的运动轨迹:
·
P
3.怎么知道蜡块的位移
上述过程怎么可以把本来发生的一个实际复杂运动,分解成了2个简单的运动,先分步求解,再合成求解?
4.怎么知道蜡块的速度
(大小,方向)
(大小,方向)
说明
1、运动的独立性
2、运动的等时性
3、运动的等效性
4、运动的同体性
a
a1
a2
v1
v2
v
运动的合成与分解是指
x、v、
a
的合成与分解。
速度、位移、加速度都是矢量,合成与分解时均遵循平行四边形定则
A
B
s
s1
s2
分速度
分速度
合速度
分加速度
合加速度
位移的合成
速度的合成
加速度的合成
分加速度
合位移
分位移
分位移
运动的合成是惟一的,而运动的分解不是惟一的,通常按运动所产生的实际效果分解。
运动的合成与分解
分运动的位置,位移,速度,加速度
合运动的位置,位移,速度,加速度
运动的合成
运动的分解
遵循平行四边形定则
独立,等时,等效
思考:上述蜡块的分运动均为匀速直线运动,那么所用的运动合成分解的思想方法在其他运动中是否还适用呢?
思考与讨论
如果物体在一个方向上的分运动是匀速直线运动,在与它垂直方向的分运动是匀加速运动,合运动的轨迹是什么样的?
P
x
=
vx
t
物体的位置P
的坐标
y
=
vy
t+
at2
1
2
y
=
x+
x2
vx
vy
2vx2
a
v
x
y
O
F合
vy
vx
1、分运动是匀速直线运动:
合运动是匀速直线运动
2、一个是匀速直线,一个是匀变速直线的合成:
合运动一定是匀变速曲线运动
3、两个都是是匀变速直线运动的合成:
(1)
若V合与a合(或F合)在一条直线上,则合运动为
直线运动。
(2)若V合与a合(或F合)不在一条直线上,则合运动
为曲线运动。
两个分运动合成时,合运动的形式:
4.合运动的性质与轨迹取决与a合与v合
的方向关系
(1)a合=0,合运动为匀速直线运动
(2)a合与v合在同一直线上,合运动为
加速或减速运动
(3)a合与v合不在同一直线上,合运动
为曲线运动
三、两直线运动的合运动的性质和轨迹
3.两个匀变速直线运动的合运动一定是
1.互成角度的两个匀速直线运动的合运动是
2.互成角度的一个匀速直线运动和一个匀变速直线运动的合运动是
⑴若合初速度方向与合加速度方向在同一条直线上时,则是
⑵若合初速度方向与合加速度方向不在同一条直线上时,则是
v
v1
v2
v
v1
v2
a1
v
v1
v2
a1
a2
a
v
v1
v2
a1
a2
a
匀速直线运动.
匀变速曲线运动.
匀变速运动.
匀变速直线运动.
(a合与v合共线)
匀变速曲线运动(a合与v合不共线).
结论
1、两个互成角度的匀速直线运动的合运动
匀速直线运动
2、两个互成角度的匀速直线运动与匀变速直线运动的合运动
匀变速曲线运动
a1
v1
a1
v1
思考与讨论
3、两个互成角度的匀变速直线运动的合运动
①两个初速度为0
的匀加速直线运动
判断几个分运动的合运动,可先把各分运动的合速度以及合加速度求出来,然后根据合速度与合加速度是否在一条直线上加以判断。
②两个初速度不为0
的匀变速直线运动
初速度为0的匀加速直线运动
匀变速直线运动
a2
v2
v
a2
v2
v
a
匀变速曲线运动
a
五、合运动性质的判定
1、两个互成角度的匀速直线运动的合运动?
2、互成角度的一个匀速直线运动和一个匀变速直线运动的合运动?
3、互成角度的两个匀变速直线运动的合运动?
一.运动的合成和分解
2.运动的合成和分解的方法
速度、位移、加速度的合成和分解——遵循平行四边形定则
1)合运动:物体实际的运动
2)分运动:与合运动等效的其它方向的运动
3)运动的合成:已知分运动求合运动
4)运动的分解:已知合运动求分运动
1.几个基本概念
x1
x2
x
v1
v2
v
a1
a2
a
x1
x2
x
3.合运动与分运动的关系
1)等效性:合运动的效果与各分运动共同产生的效果相同。
2)等时性:合运动与分运动所用时间相同。
3)独立性:各分运动各自按自己的规律运动,互不干扰。
合运动与分运动的区分原则:物体实际进行的运动一定是合运动,对应于平行四边形的对角线.
1)是直线运动还是曲线运动?(判断轨迹)
2)是匀变速运动还是变加速运动?(判断运动性质)
判断:不在一直线上的两个匀速直线运动的合运动?一个匀速直线运动与一个匀加速直线运动的合运动?两个匀变速直线运动的合运动?
思考:如何判断两个直线运动的合运动的运动轨迹和运动性质?
合力F合的方向或加速度a的方向与合速度v合的方向是否同一直线
合力或加速度是否恒定
v2
v
v2
v1
a1
a2
a
v1
v
a1
a2
a
加速直线运动
加速曲线运动
画图分析两个加速运动的合成
1、两互成角度的匀速直线运动的合成
(一定是匀速直线运动)
2、两互成角度的初速为零的匀加速直线运动的合成
(一定是匀加速直线运动)
3、两互成角度的初速不为零的匀加速直线运动的合成
(匀变速直线运动或匀变速曲线运动)
动的合成
(匀变速直线运动或匀变速曲线运动)
点评: 运动的合成
4、一个匀速直线运动和一个匀加速直线运
1、两个匀速直线
运动的合运动仍然是匀速直线运动
2、一个匀速直线运动与一个匀变速直线运动的合运动一定是曲线运动
3、两个初速度为零的匀变速直线运动合运动一定是初速度为零匀加速直线运动。合运动的方向即为合加速度的方向
4、两个初速度不为零的匀变速直线运动的合运动可能是匀变速直线运动,也可能是匀变速曲线运动
方法1.按运动的实际效果分解
方法2.正交分解
1)分解的原则
2)运动分解的典型问题
a.渡船问题的分解
b.拉绳问题的分解
4.运动的分解
合作学习:
讨论:
怎样判断两个直线运动的合运动的
轨迹是直线还是曲线?
友情提示:结合物体做曲线运动的条件!
直线运动
曲线运动
两个直线运动的合运动性质的讨论:
1、两个匀速直线运动的合运动——匀速直线运动
v1
v2
v
由两个分运动性质及合初速度与合加速度方向关系决定
2、一个匀速直线运动和一个匀变速直线运动的合运动
v0
a
v0
a
v0
g
v0
g
匀变速直线运动
v0
g
v0
g
匀变速曲线运动
3、两个匀变速直线运动的合运动
v0
v01
v02
a1
a2
a
v0
v01
v02
a1
a2
a
匀变速直线运动
匀变速曲线运动
1、两个匀速直线
运动的合运动仍然是匀速直线运动
2、一个匀速直线运动与一个匀变速直线运动的合运动一定是曲线运动
3、两个初速度为零的匀变速直线运动合运动一定是初速度为零匀加速直线运动。合运动的方向即为合加速度的方向
4、两个初速度不为零的匀变速直线运动的合运动可能是匀变速直线运动,也可能是匀变速曲线运动
合运动与分运动
【例1】关于互成角度的两个初速度不为0的匀变速直线运动的合运动,下述说法正确的是(
)
A.一定是直线运动
B.一定是抛物线运动
C.可能是直线运动,也可能是抛物线运动
D.以上说法都不对
c
小结
1、合运动与分运动的概念
3、运动的合成与分解遵循平行四边形定则
4、两个直线运动的合运动可能是直线运动,也可能是曲线运动
2、合运动与分运动的关系:独立性、等时性、等效性、同体性
运动的合成和分解的应用
———1.小船渡河
例1:一艘小船在100m宽的河中横渡到对岸,已知水流速度是3m/s,小船在静水中的速度是4m/s,求:(2)欲使船渡河时间最短,船应该怎样渡河?最短时间是多少?船经过的位移多大?
分析1:时间最短
d
结论:欲使船渡河时间最短,船头的方向应该垂直于河岸。
解1:当船头垂直河岸时,所用时间最短
最短时间
此时合速度
此时航程
例2:一艘小船在100m宽的河中横渡到对岸,已知水流速度是3m/s,小船在静水中的速度是4m/s,求:(1)欲使航行距离最短,船应该怎样渡河?渡河时间多长?
分析2:航程最短
θ
d
设船头指向与上游河岸成θ:
结论:当v船>v水时,最短航程等于河宽d。
解:2、当船头指向斜上游,与岸夹角为?时,合运动垂直河岸,航程最短,数值等于河宽100米。
过河时间:
合速度:
则cos
?
=
例3:若河宽仍为100m,已知水流速度是4m/s,小船在静水中的速度是3m/s,即船速(静水中)小于水速。
求:(1)欲使船渡河时间最短,船应该怎样渡河?
(2)欲使航行距离最短,船应该怎样渡河?最短航线是河宽吗?
θ
θ
结论:当v船<
v水时,最短航程不等于河宽d。
船头指向与上游河岸成θ:
【例题】如图所示,纤绳以恒定速率v沿水平方向通过定滑轮牵引小船靠岸,当纤绳与水面夹角为θ时,船靠岸的速度是
,若使船匀速靠岸,则纤绳的速度是
。(填:匀速、加速、减速)
【答案】
寻找分运动效果
减速
“绳+物”问题
【例题】如图所示,汽车沿水平路面以恒定速度v前进,则当拉绳与水平方向成θ角时,被吊起的物体M的速度为vM=
。
【答案】
寻找分运动效果
“绳+物”问题
【例题】如图所示,以速度v沿竖直杆匀速下滑的物体A,用细绳通过定滑轮拉动物体B在水平桌面上运动,当绳与水平面夹角为θ时,物体B的速率为
,
【答案】
vB=vsinθ
寻找分运动效果
“绳+物”问题
例:一条河宽500m,水流速度是3m/s,小船在静水中的速度是5m/s,求
(1)最短渡河的时间是多小?小船的实际位移,沿下流的位移是多少?
(2)最短位移渡河的时间是多少?最短渡河的位移是多少?
100s
【例题】一船准备渡河,已知水流速度为v2=1m/s,船在静水中的航速为v1=2m/s,则:
①要使船能够垂直地渡过河去,那么应向何方划船?
②要使船能在最短时间内渡河,应向何方划船?
平直的,洪水沿江向下游流去,水流速度为v1,摩托艇在静水中的航速为v2,战士救人的地点A离岸边最近处O的距离为d,如战士想在最短时间内将人送上岸,则摩托艇登陆的地点离O点的距离为(
)
A.dv2/
B.0
C.dv1/v2
D.dv2/v1
v22-
v12
C
【例题】.在抗洪抢险中,战士驾驶摩托艇救人,假设江岸是
