五年级下册数学教案-2.2.2 3的倍数的特征 人教版
文档属性
| 名称 | 五年级下册数学教案-2.2.2 3的倍数的特征 人教版 |

|
|
| 格式 | doc | ||
| 文件大小 | 428.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-03 00:00:00 | ||
图片预览


文档简介
课 题 3的倍数的特征 备课人
学情分析 教学设计的安排由易到难,2、5的倍数的特征与3的倍数的特征相比较,规律比较明显,教学也会相对轻松,3的倍数是比较抽象的知识,学生较难发现规律,但通过对 “2、5的倍数”的学习,相对减轻了一些难度。
学习2、5、3倍数的特征并不是很难,根据平时对学生基础的了解,部分学生数学素养较高、知识量也比较丰富,对于2、5倍数的特征已有一定的积淀,甚至3的倍数也能很快的找出来,但他们并不理解有这样的特征。因此,对于大部分学生来说,学习一个数倍数的特征存在一定的难度。
在教学中应更多的考虑到全体学生的水平,由浅入深,循序渐进地进行教学。
教学目标 知识与技能 经历在100以内的自然数表中找3的倍数的活动,在活动的基础上感悟3的倍数的特征,并尝试用自己的语言总结特征。?
过程与方法 在探索活动中,感受数学的奥妙。
情感态度与价值观 在运用规律中,体验数学的价值。
教学重难点 是3的倍数的数的特征。
教学准备
教学节数 1
一、情境导入 同学们,我们先做个游戏好吗?你能用3、5、6这三张数字卡片摆成一个2的倍数的三位数吗?
生:356和536这两个数都是2的倍数。
师:你能用同样三张卡摆一个5倍数的三位数吗?并说说你的理由?
师:你们能用这三张卡组成一个是3倍数的三位数吗?并说说你为什么这样摆放?
生:536、563、653和356应该是3的倍数。我觉得个位上是3、6、9的数是3的倍数。学生会发现问题举例来反驳。
小结:刚才同学们推理并验证了,个位上是3、6、9的数不一定是三的倍数。三的倍数到底有什么特征呢? 板书:3倍数的特征
【设计意图:学生掌握了2和5倍数的特征和这些数字的个位有关系,自然就会将这种经验迁移到3的倍数的数的特征中去。这种推广将出现偏差,然后由学生自己得出结论,再自己举例验证或修正,充分发挥学生自主探究的意识。】
二、探究新知
1、观察百数图发现3倍数的特征
师:3的倍数只看个位就能判断的方法行不通了,观察百数图圈出所有3的倍数,你有什么发现?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
师:你最先画谁?(你最先画完发现了什么?)
预设:根据百数图(乘法或口诀)可推出各个数位的数字之和都是3的倍。
(板书:3的倍数:各个数位上数字之和是3的倍数。)
师:你能用上节课的方法去验证你观察到的规律吗?为什么各个数位上数字之和是3的倍数,这个数就是三的倍数呢?
从24、45、100、126中选出一个或几个进行验证,用彩笔圈出你放心的部分,说明理由,把不用考虑的部分涂上颜色。
生动手操作,汇报自己的发现。
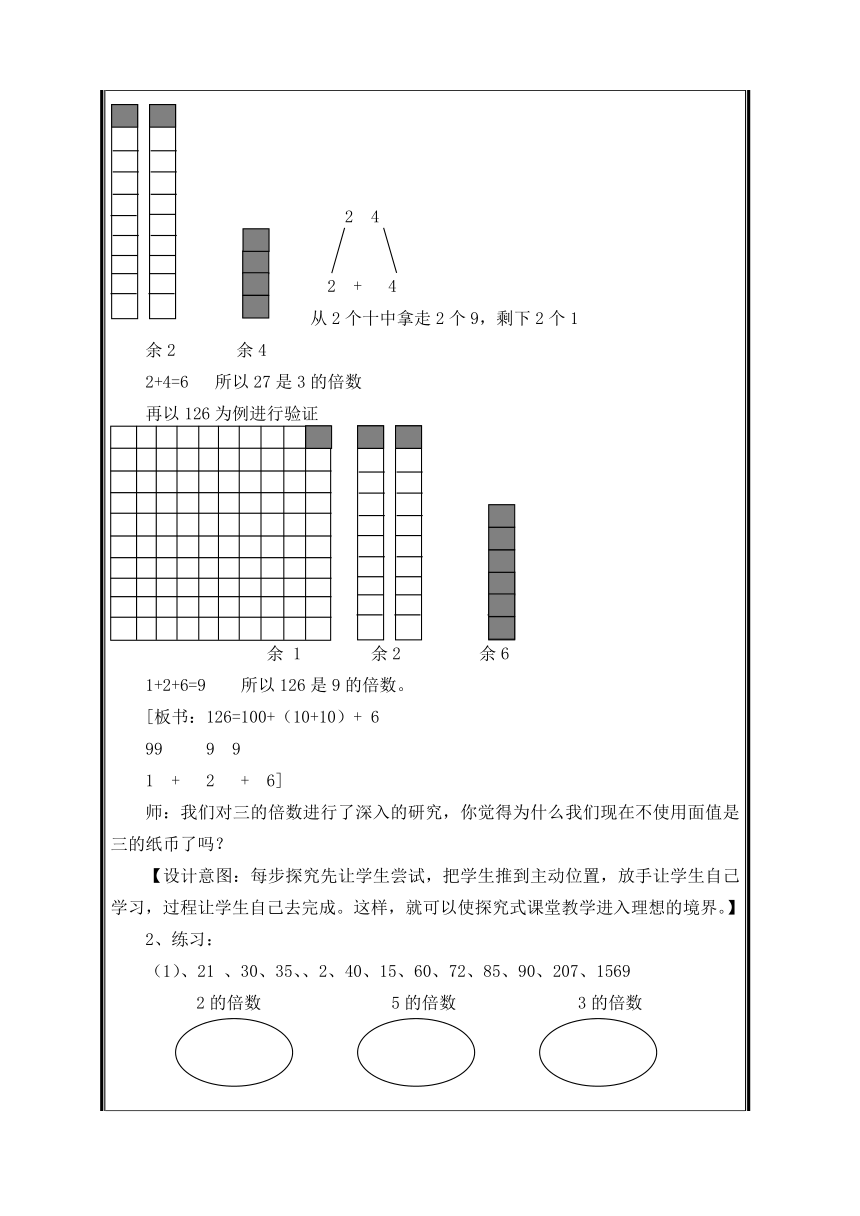
例如:24(ppt)
2 4
2 + 4
从2个十中拿走2个9,剩下2个1
余2 余4
2+4=6 所以27是3的倍数
再以126为例进行验证
余 1 余2 余6
1+2+6=9 所以126是9的倍数。
[板书:126=100+(10+10)+ 6
99 9 9
1 + 2 + 6]
师:我们对三的倍数进行了深入的研究,你觉得为什么我们现在不使用面值是三的纸币了吗?
【设计意图:每步探究先让学生尝试,把学生推到主动位置,放手让学生自己学习,过程让学生自己去完成。这样,就可以使探究式课堂教学进入理想的境界。】
2、练习:
(1)、21 、30、35、、2、40、15、60、72、85、90、207、1569
2的倍数 5的倍数 3的倍数
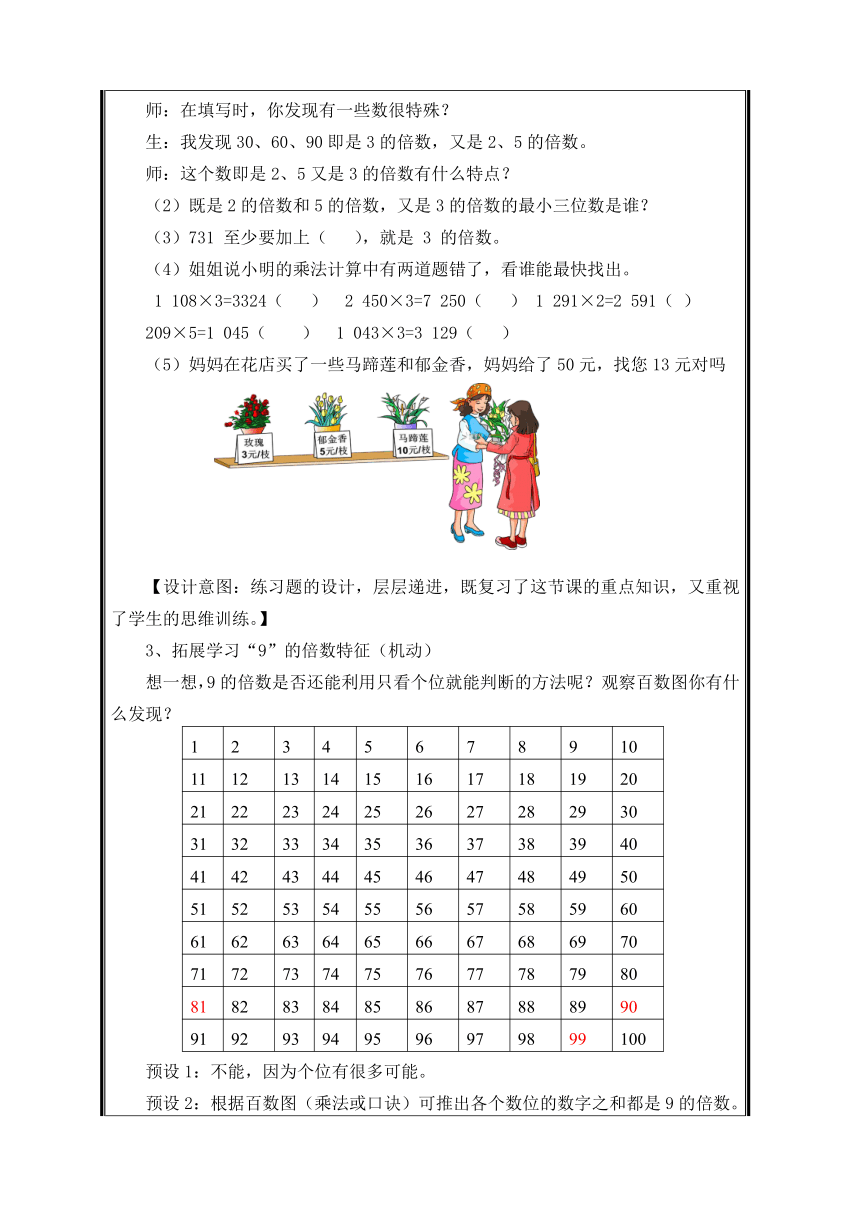
师:在填写时,你发现有一些数很特殊?
生:我发现30、60、90即是3的倍数,又是2、5的倍数。
师:这个数即是2、5又是3的倍数有什么特点?
(2)既是2的倍数和5的倍数,又是3的倍数的最小三位数是谁?
(3)731 至少要加上( ),就是 3 的倍数。
(4)姐姐说小明的乘法计算中有两道题错了,看谁能最快找出。
1 108×3=3324( ) 2 450×3=7 250( ) 1 291×2=2 591( )
209×5=1 045( ) 1 043×3=3 129( )
(5)妈妈在花店买了一些马蹄莲和郁金香,妈妈给了50元,找您13元对吗
【设计意图:练习题的设计,层层递进,既复习了这节课的重点知识,又重视了学生的思维训练。】
3、拓展学习“9”的倍数特征(机动)
想一想,9的倍数是否还能利用只看个位就能判断的方法呢?观察百数图你有什么发现?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
预设1:不能,因为个位有很多可能。
预设2:根据百数图(乘法或口诀)可推出各个数位的数字之和都是9的倍数。
(板书:9的倍数:各个数位上数字之和是9的倍数。)
师:解释27(ppt)
2 7
2 + 7
从2个十中拿走2个9,剩下2个1
余2 余7
2+7=9 所以27是9的倍数
再以126为例进行验证
余 1 余2 余6
1+2+6=9 所以126是9的倍数
【设计意图:把思考的权利教给学生,把交流的权利交给给学生,发展学生的思维的灵活性。】
4、课堂总结
自然数无穷无尽的延伸着,我们对它是如此的熟悉,但是,对它的发现,却令人如此的惊奇,有一位数学家高斯曾说过:“人们通常把数学誉为科学的皇后,而专门研究自然数性质的数学分支------‘数论’,则是数学皇后头顶上的皇冠。”当我们真正走进自然数的王国,展现在我们面前的将是浩瀚而又神奇的世界,通过对它的研究能让你体会数学学习的乐趣。
巩 固 深 化
一、自学检测 (一)判断对错。(对的打“√”,错的打“×”)
1、个位上是3,6,9的数一定是3的倍数。 ( )
2、9的倍数一定是3的倍数。( )
3、一个数各个数位上的数都是3的倍数,这个数也一定是3的数。 ( )
4、用2,3,4三个数字组成的三位数一定是3的倍数。( )
5、个位上是6的数一定是2和3的倍数。 ( )
【活动形式】独立完成,小组汇报
【要点提炼】小结3的倍数特征。
(二)填空
1、一个数( )上的数的( )是3的倍数,这个数就是3的倍数。
2、是3的倍数的最小的三位数是( ),最大三位数是( )。
3、既是2的倍数又是3的倍数的最小两位数是( )。
二、练习
1、在41、23、609、66、45、89、60、78、34、63、330、32、102、69、48、318、622、数中,
3的倍数有:( )。
2的倍数有:( )。
既是2和5的倍数,又是3的倍数的有:( )。
2、在 里填上一个数字,使每个数都是3的倍数。
2 1 3 5
7 52 4 13
3、按要求写数。
(1)写出五个是3的倍数的偶数。
(2)写出五个是5的倍数的奇数。
(3)从2、6、7、5四个数中,选出三个组成一个三位数,使它是3的倍数。这样的数有几个?写出来。
4、货场有96吨的煤,现有(1)号、(2)号、(3)号、三种不同的载重量的卡车,用几号车正好可以装完?
(1)号
(2)号
(3)号
2吨
3吨
5吨
【活动形式】独立完成,小组汇报,学生展示。
【要点提炼】利用3的倍数的特征来判断一个数是不是3的倍数,运用它来解决生活中的实际问题。
三、课堂检测
两导两练达标检测。
四、拓展延伸
1、舞蹈队有若干人,如果在列队时12人站一排,则余5人,如果15人站一排,还是余5人,这个舞蹈队至少有多少人?
2、食品店运来80个面包,如果2个一袋能正好装完吗?如果5个一袋,能正好装完吗?为什么?如果每袋装3个,至少还需要再运来多少个面包?
【活动形式】学生独立思考、讨论。
【要点提炼】考查学生运用相关知识解决生活中实际问题的能力。
五、课堂总结
这节课你有何收获?
板 书 设 计
3 的倍数的特征 3的倍数:一个数各位上的数的和是 3 的倍数。
126=100+(10+10)+ 6
99 9 9
1 + 2 + 6
9的倍数:各个数位上数字之和是9的倍数
教 学 反 思
在前面学习了2和5的倍数特征的基础上进行了“3的倍数的特征”这节课。本节课突出的特点主要有以下两点: 1.注意学生的基础知识,促进知识迁移。学生自身所具备的知识与经验是重要的课堂资源,在必要的环节放手,调动学生在已有的知识的基础上探索3的倍数特征。是学生利用相关旧知识,寻求它与新知识之间的共同因素,亲身感受一个完整的迁移过程,使学生自主的探究并深入理解新的知识。
2.把课堂交给学生,学生是课堂的主体。本节课从始至终都是引导学生去发现问题,研究问题,解决问题,充分调动学生学习的自主性,满足学生自主学习的需要,尊重学生的主体地位,发挥学生的主体作用,使学生实实在在经历这一过程,扎扎实实收获这一过程。
这节课的不足之处是,最后总结3的倍数特征时,没有充分放手让学生多说、说透,这样更有助于增强学生的归纳概括能力。在练习题方面,也应形式多样化,如用卡片练习判断,这样效率更高,课堂氛围活跃,学生的思维会更集中。举反例会让学生反方向去学习知识。总之,方法是需要教师提升、学生感悟的。
学情分析 教学设计的安排由易到难,2、5的倍数的特征与3的倍数的特征相比较,规律比较明显,教学也会相对轻松,3的倍数是比较抽象的知识,学生较难发现规律,但通过对 “2、5的倍数”的学习,相对减轻了一些难度。
学习2、5、3倍数的特征并不是很难,根据平时对学生基础的了解,部分学生数学素养较高、知识量也比较丰富,对于2、5倍数的特征已有一定的积淀,甚至3的倍数也能很快的找出来,但他们并不理解有这样的特征。因此,对于大部分学生来说,学习一个数倍数的特征存在一定的难度。
在教学中应更多的考虑到全体学生的水平,由浅入深,循序渐进地进行教学。
教学目标 知识与技能 经历在100以内的自然数表中找3的倍数的活动,在活动的基础上感悟3的倍数的特征,并尝试用自己的语言总结特征。?
过程与方法 在探索活动中,感受数学的奥妙。
情感态度与价值观 在运用规律中,体验数学的价值。
教学重难点 是3的倍数的数的特征。
教学准备
教学节数 1
一、情境导入 同学们,我们先做个游戏好吗?你能用3、5、6这三张数字卡片摆成一个2的倍数的三位数吗?
生:356和536这两个数都是2的倍数。
师:你能用同样三张卡摆一个5倍数的三位数吗?并说说你的理由?
师:你们能用这三张卡组成一个是3倍数的三位数吗?并说说你为什么这样摆放?
生:536、563、653和356应该是3的倍数。我觉得个位上是3、6、9的数是3的倍数。学生会发现问题举例来反驳。
小结:刚才同学们推理并验证了,个位上是3、6、9的数不一定是三的倍数。三的倍数到底有什么特征呢? 板书:3倍数的特征
【设计意图:学生掌握了2和5倍数的特征和这些数字的个位有关系,自然就会将这种经验迁移到3的倍数的数的特征中去。这种推广将出现偏差,然后由学生自己得出结论,再自己举例验证或修正,充分发挥学生自主探究的意识。】
二、探究新知
1、观察百数图发现3倍数的特征
师:3的倍数只看个位就能判断的方法行不通了,观察百数图圈出所有3的倍数,你有什么发现?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
师:你最先画谁?(你最先画完发现了什么?)
预设:根据百数图(乘法或口诀)可推出各个数位的数字之和都是3的倍。
(板书:3的倍数:各个数位上数字之和是3的倍数。)
师:你能用上节课的方法去验证你观察到的规律吗?为什么各个数位上数字之和是3的倍数,这个数就是三的倍数呢?
从24、45、100、126中选出一个或几个进行验证,用彩笔圈出你放心的部分,说明理由,把不用考虑的部分涂上颜色。
生动手操作,汇报自己的发现。
例如:24(ppt)
2 4
2 + 4
从2个十中拿走2个9,剩下2个1
余2 余4
2+4=6 所以27是3的倍数
再以126为例进行验证
余 1 余2 余6
1+2+6=9 所以126是9的倍数。
[板书:126=100+(10+10)+ 6
99 9 9
1 + 2 + 6]
师:我们对三的倍数进行了深入的研究,你觉得为什么我们现在不使用面值是三的纸币了吗?
【设计意图:每步探究先让学生尝试,把学生推到主动位置,放手让学生自己学习,过程让学生自己去完成。这样,就可以使探究式课堂教学进入理想的境界。】
2、练习:
(1)、21 、30、35、、2、40、15、60、72、85、90、207、1569
2的倍数 5的倍数 3的倍数
师:在填写时,你发现有一些数很特殊?
生:我发现30、60、90即是3的倍数,又是2、5的倍数。
师:这个数即是2、5又是3的倍数有什么特点?
(2)既是2的倍数和5的倍数,又是3的倍数的最小三位数是谁?
(3)731 至少要加上( ),就是 3 的倍数。
(4)姐姐说小明的乘法计算中有两道题错了,看谁能最快找出。
1 108×3=3324( ) 2 450×3=7 250( ) 1 291×2=2 591( )
209×5=1 045( ) 1 043×3=3 129( )
(5)妈妈在花店买了一些马蹄莲和郁金香,妈妈给了50元,找您13元对吗
【设计意图:练习题的设计,层层递进,既复习了这节课的重点知识,又重视了学生的思维训练。】
3、拓展学习“9”的倍数特征(机动)
想一想,9的倍数是否还能利用只看个位就能判断的方法呢?观察百数图你有什么发现?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
预设1:不能,因为个位有很多可能。
预设2:根据百数图(乘法或口诀)可推出各个数位的数字之和都是9的倍数。
(板书:9的倍数:各个数位上数字之和是9的倍数。)
师:解释27(ppt)
2 7
2 + 7
从2个十中拿走2个9,剩下2个1
余2 余7
2+7=9 所以27是9的倍数
再以126为例进行验证
余 1 余2 余6
1+2+6=9 所以126是9的倍数
【设计意图:把思考的权利教给学生,把交流的权利交给给学生,发展学生的思维的灵活性。】
4、课堂总结
自然数无穷无尽的延伸着,我们对它是如此的熟悉,但是,对它的发现,却令人如此的惊奇,有一位数学家高斯曾说过:“人们通常把数学誉为科学的皇后,而专门研究自然数性质的数学分支------‘数论’,则是数学皇后头顶上的皇冠。”当我们真正走进自然数的王国,展现在我们面前的将是浩瀚而又神奇的世界,通过对它的研究能让你体会数学学习的乐趣。
巩 固 深 化
一、自学检测 (一)判断对错。(对的打“√”,错的打“×”)
1、个位上是3,6,9的数一定是3的倍数。 ( )
2、9的倍数一定是3的倍数。( )
3、一个数各个数位上的数都是3的倍数,这个数也一定是3的数。 ( )
4、用2,3,4三个数字组成的三位数一定是3的倍数。( )
5、个位上是6的数一定是2和3的倍数。 ( )
【活动形式】独立完成,小组汇报
【要点提炼】小结3的倍数特征。
(二)填空
1、一个数( )上的数的( )是3的倍数,这个数就是3的倍数。
2、是3的倍数的最小的三位数是( ),最大三位数是( )。
3、既是2的倍数又是3的倍数的最小两位数是( )。
二、练习
1、在41、23、609、66、45、89、60、78、34、63、330、32、102、69、48、318、622、数中,
3的倍数有:( )。
2的倍数有:( )。
既是2和5的倍数,又是3的倍数的有:( )。
2、在 里填上一个数字,使每个数都是3的倍数。
2 1 3 5
7 52 4 13
3、按要求写数。
(1)写出五个是3的倍数的偶数。
(2)写出五个是5的倍数的奇数。
(3)从2、6、7、5四个数中,选出三个组成一个三位数,使它是3的倍数。这样的数有几个?写出来。
4、货场有96吨的煤,现有(1)号、(2)号、(3)号、三种不同的载重量的卡车,用几号车正好可以装完?
(1)号
(2)号
(3)号
2吨
3吨
5吨
【活动形式】独立完成,小组汇报,学生展示。
【要点提炼】利用3的倍数的特征来判断一个数是不是3的倍数,运用它来解决生活中的实际问题。
三、课堂检测
两导两练达标检测。
四、拓展延伸
1、舞蹈队有若干人,如果在列队时12人站一排,则余5人,如果15人站一排,还是余5人,这个舞蹈队至少有多少人?
2、食品店运来80个面包,如果2个一袋能正好装完吗?如果5个一袋,能正好装完吗?为什么?如果每袋装3个,至少还需要再运来多少个面包?
【活动形式】学生独立思考、讨论。
【要点提炼】考查学生运用相关知识解决生活中实际问题的能力。
五、课堂总结
这节课你有何收获?
板 书 设 计
3 的倍数的特征 3的倍数:一个数各位上的数的和是 3 的倍数。
126=100+(10+10)+ 6
99 9 9
1 + 2 + 6
9的倍数:各个数位上数字之和是9的倍数
教 学 反 思
在前面学习了2和5的倍数特征的基础上进行了“3的倍数的特征”这节课。本节课突出的特点主要有以下两点: 1.注意学生的基础知识,促进知识迁移。学生自身所具备的知识与经验是重要的课堂资源,在必要的环节放手,调动学生在已有的知识的基础上探索3的倍数特征。是学生利用相关旧知识,寻求它与新知识之间的共同因素,亲身感受一个完整的迁移过程,使学生自主的探究并深入理解新的知识。
2.把课堂交给学生,学生是课堂的主体。本节课从始至终都是引导学生去发现问题,研究问题,解决问题,充分调动学生学习的自主性,满足学生自主学习的需要,尊重学生的主体地位,发挥学生的主体作用,使学生实实在在经历这一过程,扎扎实实收获这一过程。
这节课的不足之处是,最后总结3的倍数特征时,没有充分放手让学生多说、说透,这样更有助于增强学生的归纳概括能力。在练习题方面,也应形式多样化,如用卡片练习判断,这样效率更高,课堂氛围活跃,学生的思维会更集中。举反例会让学生反方向去学习知识。总之,方法是需要教师提升、学生感悟的。
